线段树的学习(2023.4.5)
今天我来学习线段树
首先它是树有着'树'的结构,线段树由于本身是专门用来处理区间问题的
它的作用可以处理区间的问题拥有更快的速度.
对于每一个子节点而言,都表示整个序列中的一段子区间;对于每个叶子节点而言,都表示序列中的单个元素信息;子节点不断向自己的父亲节点传递信息,而父节点存储的信息则是他的每一个子节点信息的整合(信息的整合可能是求和,也可能是最大值,也可能是最小值)。
就是一个分块的思想.
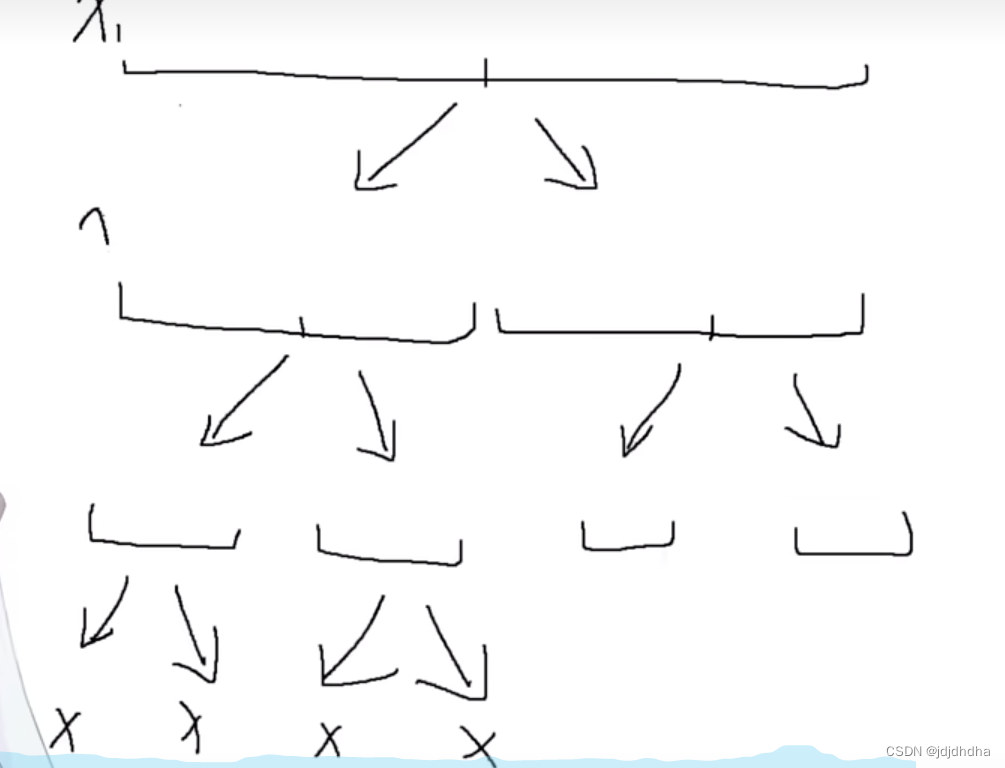
一个大的区间不断的被二分找到区间的长度为1,
如上图每一个区间就是一个节点.
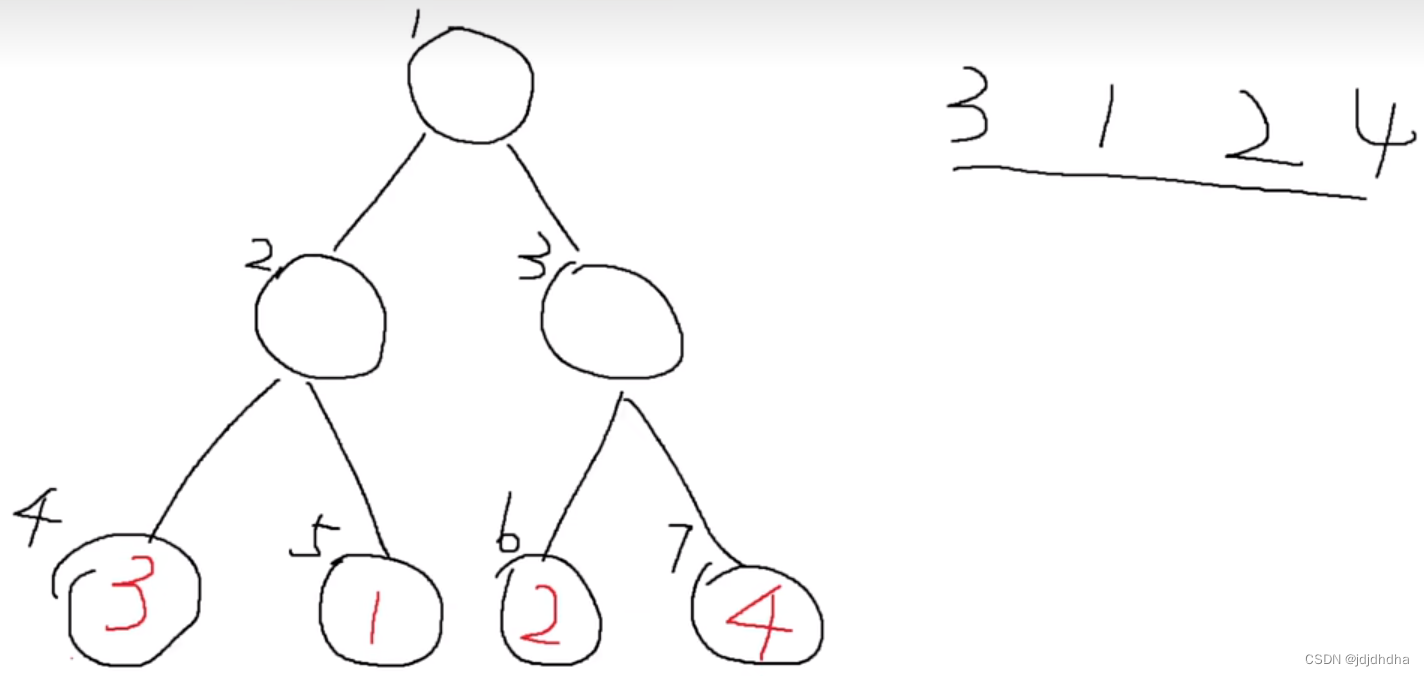
数组3 1 2 4 就如上图一般
1节点代表区间1到4
2为1到2 3表示3到4
由于线段树满足完全二叉树,
节点x的左子节点为2x
右子节点为2x+1
用数组非长好的就可以实现.
以下的代码我一求区间的和为样例,用数组来模拟树的节点
int lchid(int x){//找左兒子
return 2*x;}int rchid(int x){//找右兒子
return 2*x+1;}
这两函数就是直接找到你的二子的下标的. (其实也可以不写的,但是有的话调用就好了完全不用想).
这里选定的是求和的关系
tree数组的树的节点
void sum(int p){//向上维护(求和)
tree[p]=tree[lchid(p)]+tree[rchid(p)];
}然后就是建树
p是当前节点的下标,l和r是p节点的区间标
void build(int p,int l,int r){
if(r==l){tree[p]=a[l];return ;
}
int mid=(l+r)/2;
build(lchid(p),l,mid);//向左边的区间递归
build(rchid(p),mid+1,r);//向右区间进行递归
sum(p);//对当前的节点进行维护(赋值);
}
//区间建树到了区间长度为一的节点就赋值(给叶子节点赋值)
用到是是递归,一直递归下去要是出现赋值的数目超过了比如区间为3但是会有4个叶子节点
直接赋值为0即可
有时我们要修改某个区间的值
void updata(int ll,int rr,int l,int r,int p,int k){
//ll,rr是要修改的区间
//l,r是当前节点的区间p是当前节点的编号
//k是要修改的值(可能是加,也可能是减)if(ll<=l&&rr>=r){//修改的区间完全包含当前区间lazyr(l,r,p,k);return ;
}
donm(p,l,r);
//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) updata(ll,rr,l,mid,lchid(p),k);if(rr>mid) updata(ll,rr,mid+1,r,rchid(p),k);sum(p);//对当前的节点要更新的}
//区间修改
void lazyr(int l,int r,int p,int k){//改变区间的和,并打上lazy标记
lazy[p]+=k;
tree[p]+=k*(r-l+1);
}void donm(int p,int l,int r){//k就是p节点的lazy值,向下传递lazy值int mid=(l+r)/2;lazyr(l,mid,lchid(p),lazy[p]);lazyr(mid+1,r,rchid(p),lazy[p]);lazy[p]=0;//把lazy向下传递后自己的lazy清空}你会问为啥要这样写
1,线段树在对区间处理时是用当前的区间与要处理的区间的包含关系来处理的
2类情况
1操作的区间包含当前的区间,就直接返回当前节点的区间值
2只有左或者右区间的端点包含,那就递归下去知道包含为止
2.为何要用到lazy数组以及donm函数
注意重点来了!
如果我们要对区间的值进行修改,非要递归到区间长度为一的时候进行修改,那线段树比起简单的数组处理区间就完全没有优势了,复杂度还会略高一点
所以就有了,每个节点的lazy值
lazy值就是要改的区间与包含当前的区间
那就不用继续往下更新了,直接把此节点的区间的值改了并且给一个lazy值表示这个节点,的子节点还未更新,要更新的值就是p的lazy值
我们不更新下面的值那下面的值不是错了吗?
当然有方法的,下次当我们要递归到本节点的子节点是
要判断当前的节点的lazy值(>0就是存在)
那就更新两个子节点的值即可,也不用再往下了.
这样就不会一修改就直接到叶子节点了
要用到了再修改
思想就是延迟更新
区间求和
ll find(int ll,int rr,int l,int r,int p){if(ll<=l&&rr>=r){//修改的区间完全包含当前区间ans+=tree[p];return 0;}
donm(p,l,r);//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) find(ll,rr,l,mid,lchid(p));if(rr>mid) find(ll,rr,mid+1,r,rchid(p));return ans;
}依旧是递归遍历
要是要用到子节点就以lazy判断要不要更新(我没判断,lazy=0,在函数中不会对数据有改变,但是判断了运行速度会快一点点)
ok讲了这摩多
来个板子吧!
复制Markdown 展开
题目描述
如题,已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 �k。
- 求出某区间每一个数的和。
输入格式
第一行包含两个整数 �,�n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 �n 个用空格分隔的整数,其中第 �i 个数字表示数列第 �i 项的初始值。
接下来 �m 行每行包含 33 或 44 个整数,表示一个操作,具体如下:
1 x y k:将区间 [�,�][x,y] 内每个数加上 �k。2 x y:输出区间 [�,�][x,y] 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
输入输出样例
输入 #1复制
5 5 1 5 4 2 3 2 2 4 1 2 3 2 2 3 4 1 1 5 1 2 1 4
输出 #1复制
11 8 20
说明/提示
对于 30%30% 的数据:�≤8n≤8,�≤10m≤10。
对于 70%70% 的数据:�≤103n≤103,�≤104m≤104。
对于 100%100% 的数据:1≤�,�≤1051≤n,m≤105。
保证任意时刻数列中所有元素的绝对值之和 ≤1018≤1018。
【样例解释】
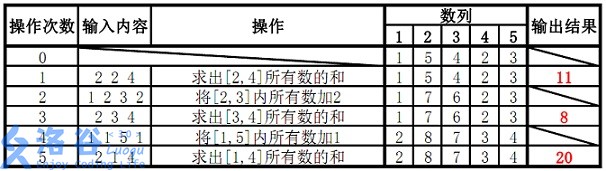
出自洛谷:p3372
#include<stdio.h>
#define maxsize 100000
typedef long long ll;//long long 麻烦好长的就用ll
ll tree[maxsize*4];//用數字模擬樹
int lazy[maxsize*4]={0};//lazy數組
int a[100050];
ll ans=0;int lchid(int x){//找左兒子
return 2*x;}int rchid(int x){//找右兒子
return 2*x+1;}void sum(int p){//向上维护(求和)
tree[p]=tree[lchid(p)]+tree[rchid(p)];
}void lazyr(int l,int r,int p,int k){//改变区间的和,并打上lazy标记
lazy[p]+=k;
tree[p]+=k*(r-l+1);
}void donm(int p,int l,int r){//k就是p节点的lazy值,向下传递lazy值int mid=(l+r)/2;lazyr(l,mid,lchid(p),lazy[p]);lazyr(mid+1,r,rchid(p),lazy[p]);lazy[p]=0;//把lazy向下传递后自己的lazy清空}
//lazy下传的函数void build(int p,int l,int r){
if(r==l){tree[p]=a[l];return ;
}
int mid=(l+r)/2;
build(lchid(p),l,mid);//向左边的区间递归
build(rchid(p),mid+1,r);//向右区间进行递归
sum(p);//对当前的节点进行维护(赋值);
}
//区间建树void updata(int ll,int rr,int l,int r,int p,int k){
//ll,rr是要修改的区间
//l,r是当前节点的区间p是当前节点的编号
//k是要修改的值(可能是加,也可能是减)if(ll<=l&&rr>=r){//修改的区间完全包含当前区间lazyr(l,r,p,k);return ;
}
donm(p,l,r);
//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) updata(ll,rr,l,mid,lchid(p),k);if(rr>mid) updata(ll,rr,mid+1,r,rchid(p),k);sum(p);//对当前的节点要更新的}
//区间修改ll find(int ll,int rr,int l,int r,int p){if(ll<=l&&rr>=r){//修改的区间完全包含当前区间ans+=tree[p];return 0;}
donm(p,l,r);//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) find(ll,rr,l,mid,lchid(p));if(rr>mid) find(ll,rr,mid+1,r,rchid(p));return ans;
}
//区间求和int main(){int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);build(1,1,n);//起始点为1,区间为1到n的建树
while(m--){int q,w,e,r;scanf("%d",&q);if(q==1){scanf("%d%d%d",&w,&e,&r);updata(w,e,1,n,1,r);}else{ans=0;scanf("%d%d",&w,&e);printf("%lld\n",find(w,e,1,n,1));}
}
return 0;
}
没得解释,就是板子题,算法的每一行都有我的理解和注释
该算法刚学不熟悉,看着大佬的题解来的
每一行都尽量的去理解
这就是我的忍道!
ok 撒花谢幕!!!!!
相关文章:

线段树的学习(2023.4.5)
今天我来学习线段树 首先它是树有着树的结构,线段树由于本身是专门用来处理区间问题的 它的作用可以处理区间的问题拥有更快的速度. 对于每一个子节点而言,都表示整个序列中的一段子区间;对于每个叶子节点而言,都表示序列中的单个元素信息…...
Java 实现excel、word、txt、ppt等办公文件在线预览功能
相信大家在开发的过程中都会遇到在线预览功能,有没有想过如何通过java来实现excel、word、txt、ppt等办公文件在线预览功能?今天我们就来解决这一疑问! 其实,网上还是有些公司对这一功能提供了收费服务。那么,如何实现…...

《Vue3实战》 第九章 路由
1、安装路由 cnpm install vue-router42、router-link应用 2.1、创建views/OrderList.vue组件 <template> <h1>订单列表页面......</h1> </template> <script> export default{name: OrderList,data(){return{arr:[4,2,5]} } …...

ToBeWritten之物联网Zigbee协议
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...

【万象奥科】RZ/G2UL网关内存压力测试
测试目的 内存压力测试的目的是测试系统内存的稳定性和可靠性,以便确定系统是否能够在各种负载情况下正常运行。其主要目的有: 测试内存的正确性:通过模拟各种内存负载情况,例如写入随机数据、重复写入相同数据、使用指定的模式…...
C++中的继承
面向对象的三大特性 封装继承多态 继承的概念和定义 继承的本质就是类层次的复用。 继承的概念继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段.它允许程序员在保持原有类特性的基础上进行扩展,增加功能,这样产生新的类…...
SpringRetry接口异常优雅重试机制
场景: 某些场景下,如果接口出现异常需要进行重试,例如网络抖动、调用接口超时等并非接口代码导致的报错,此时可以进行接口重试机制 1、导入 spring retry 重试依赖 <!-- spring retry --><dependency><groupId>…...

2023年全国最新高校辅导员精选真题及答案46
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 27.充沛的精力和顽强的毅力是教师意志品质的体现。 答案:正确 28.规范与约束…...

程序员为了女朋you进了华为,同学去了阿里,2年后对比收入懵了
什么样的工作才是好工作?每当遇到这个问题,我们的答案总是出奇的一致:钱多事少离家近。 然而现实总是残酷的,日前,有网友在某社交论坛发帖称:自己为了女朋友留在了成都进入华为工作,而自己的同…...
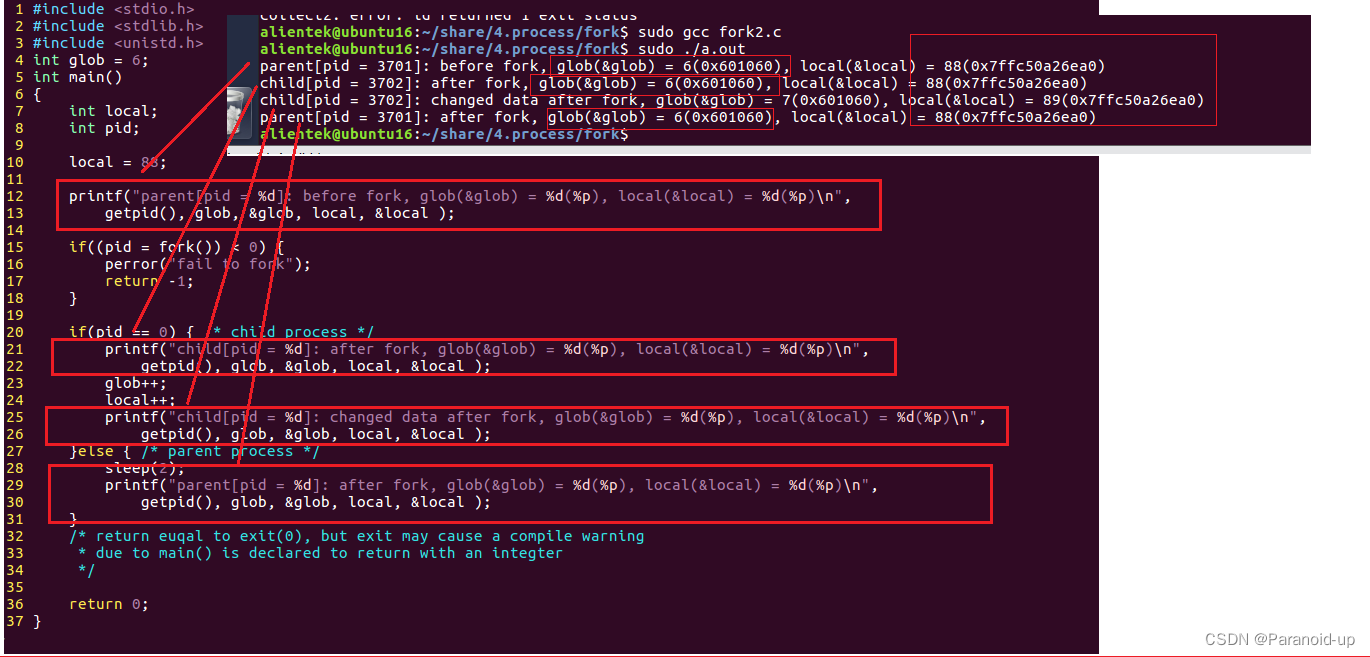
Linux中的算法分离手段
0. 简介 参数分离对于绝大多数算法开发来说收益是非常大的,因为我们都知道,随着平台的更替,很多时候如果说数据流和算法交叠在一起(即接口与实现合在一起)。这将有可能会导致在迁移平台时候会导致代码难以维护&#x…...
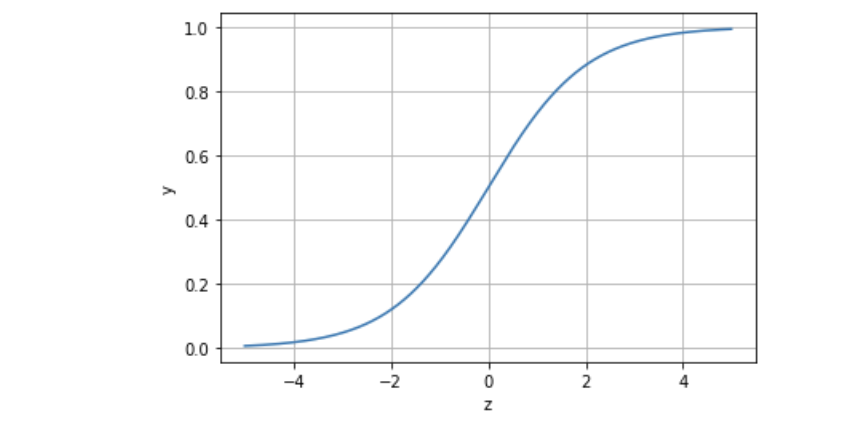
机器学习实战:Python基于Logistic逻辑回归进行分类预测
目录1 前言1.1 Logistic回归的介绍1.2 Logistic回归的应用2 iris数据集数据处理2.1 导入函数2.2 导入数据2.3 简单数据查看3 可视化3.1 条形图/散点图3.2 箱线图3.3 三维散点图4 建模预测4.1 二分类预测4.2 多分类预测5 讨论1 前言 1.1 Logistic回归的介绍 逻辑回归ÿ…...
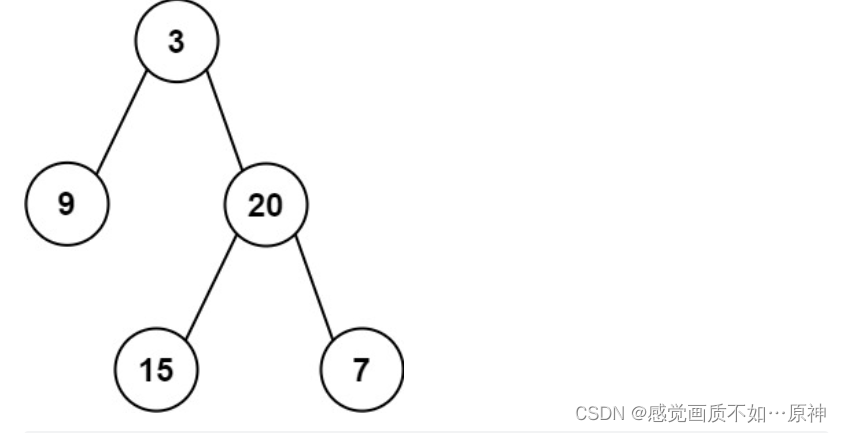
Leetcode.404 左叶子之和
题目链接 Leetcode.404 左叶子之和 easy 题目描述 给定二叉树的根节点 root,返回所有 左叶子 之和。 示例 1: 输入: root [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以…...

Android 11.0 原生SystemUI下拉通知栏UI背景设置为圆角背景的定制(二)
1.前言 在11.0的系统rom定制化开发中,在原生系统SystemUI下拉状态栏的下拉通知栏的背景默认是白色四角的背景, 由于在产品设计中,在对下拉通知栏通知的背景需要把四角背景默认改成圆角背景,所以就需要分析系统原生下拉通知栏的每条通知的默认背景, 然后通过systemui的通知…...

C语言CRC-16 IBM格式校验函数
C语言CRC-16 IBM格式校验函数 CRC-16校验产生2个字节长度的数据校验码,通过计算得到的校验码和获得的校验码比较,用于验证获得的数据的正确性。基本的CRC-16校验算法实现,参考: C语言标准CRC-16校验函数。 不同厂家通过对输入数…...
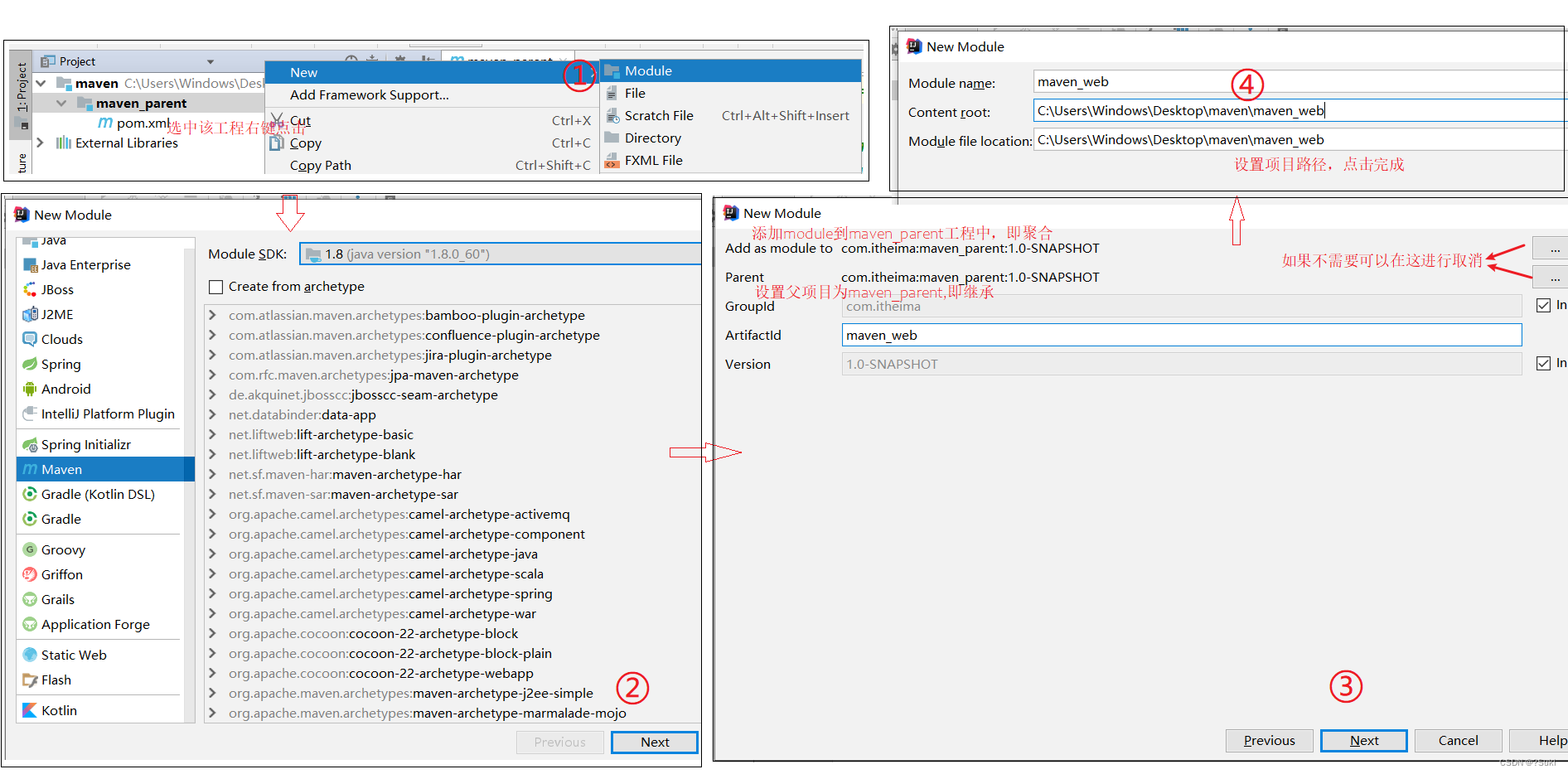
Maven高级-聚合和继承
Maven高级-聚合和继承3,聚合和继承3.1 聚合步骤1:创建一个空的maven项目步骤2:将项目的打包方式改为pom步骤3:pom.xml添加所要管理的项目步骤4:使用聚合统一管理项目3.2 继承步骤1:创建一个空的Maven项目并将其打包方式设置为pom步骤2:在子项目中设置其父工程步骤3:…...

如何写出10万+ Facebook 贴文?
想要创作一篇优秀的Facebook贴文,首先要考虑以下几个问题: 1.文案特点 一篇清晰简洁的文案有助于受众在有限的浏览时间内快速了解你想要展示的信息。根据以往经验,文案内容最好保持在20个汉字以内,加上链接描述最好也不要超过50…...

图像处理数据集
BSDS500 Berkeley Segmentation Dataset 500 是第一个用于评估超像素算法的数据集。对于参数优化,使用了验证集。 500张数据集200训练集train100验证集val200测试集test 每张图像有 5 个不同的高质量地面真值分割(groundTruth,是.mat文件) …...
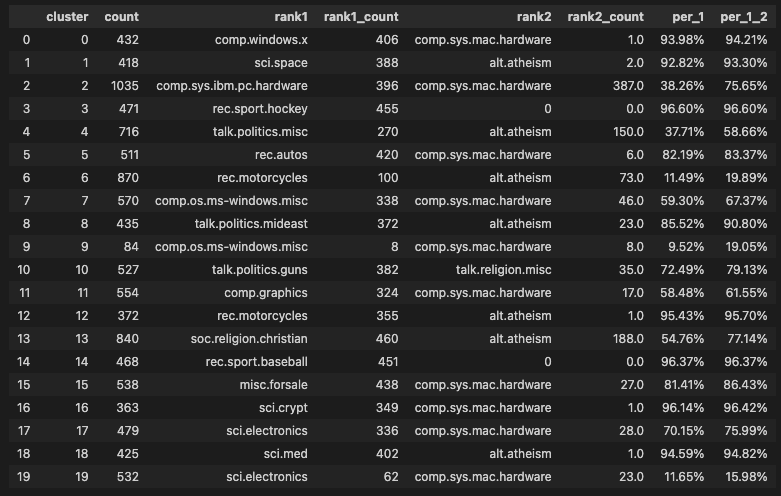
文本聚类与摘要,让AI帮你做个总结
你好,我是徐文浩。 上一讲里,我们用上了最新的ChatGPT的API,注册好了HuggingFace的账号,也把我们的聊天机器人部署了出去。希望通过这个过程,你对实际的应用开发过程已经有了充足的体验。那么这一讲里,我们…...
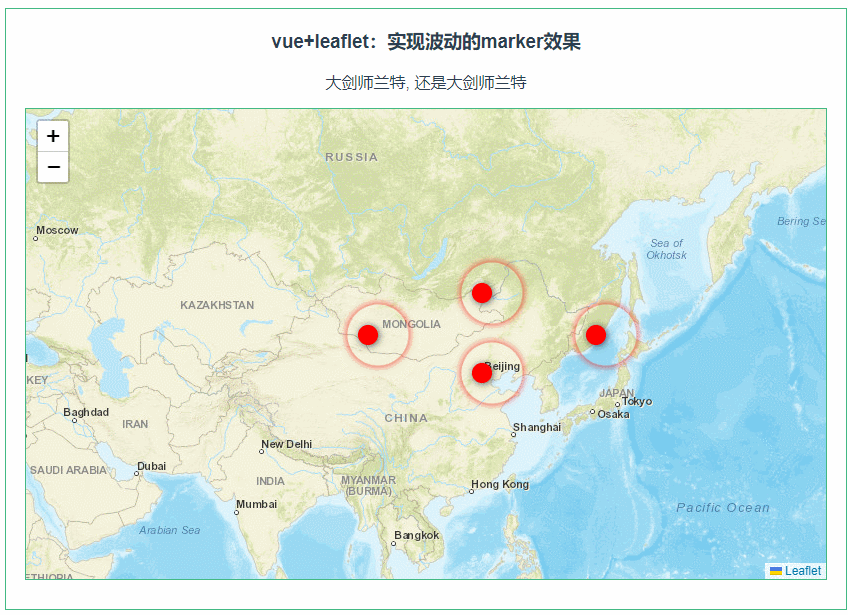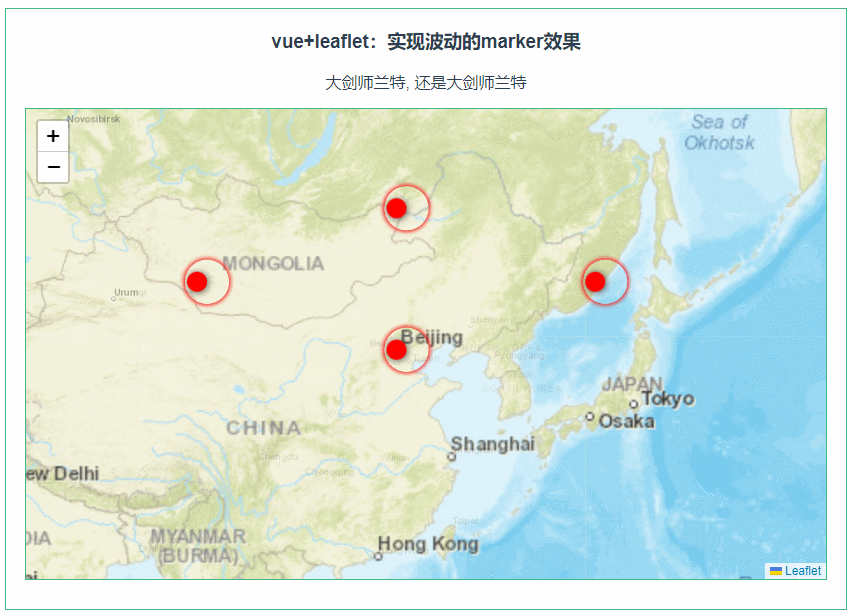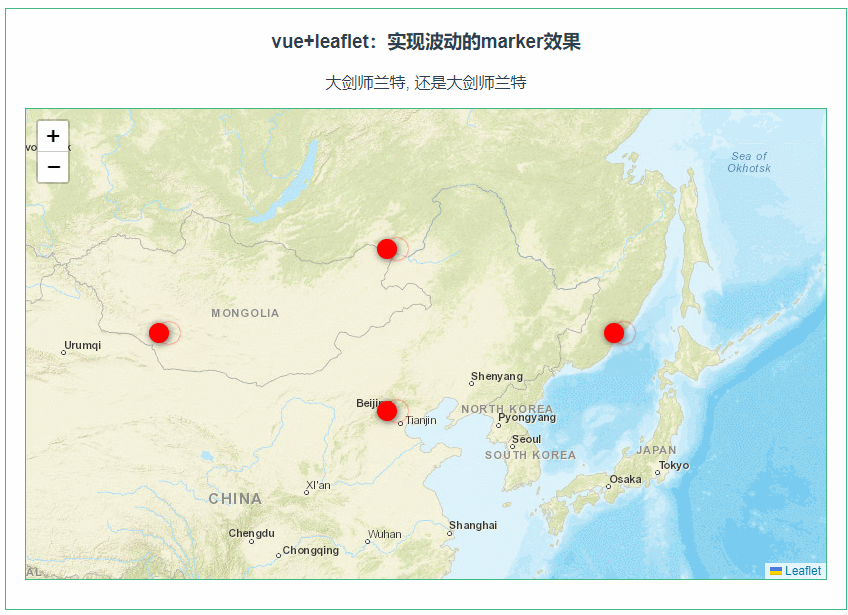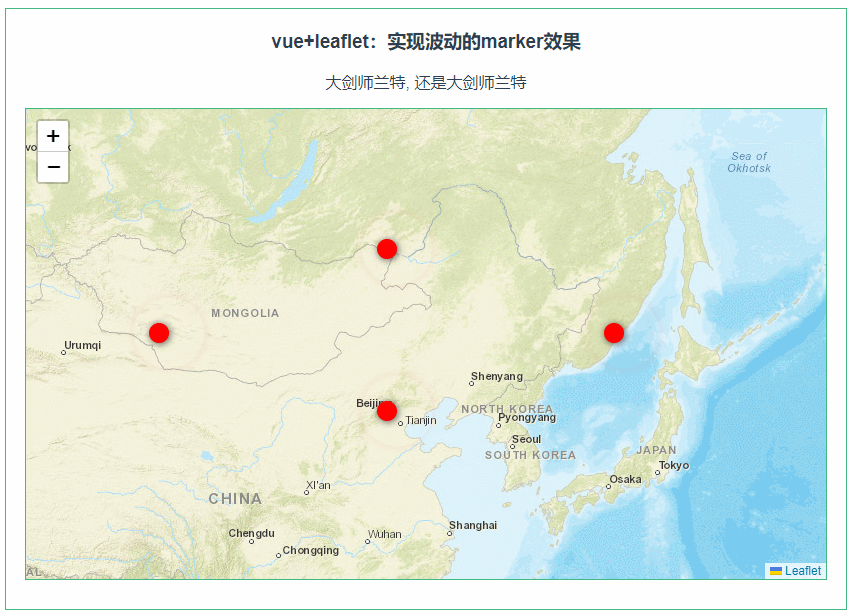
leaflet实现波动的marker效果(131)
第131个 点击查看专栏目录 本示例的目的是介绍如何在vue+leaflet中显示波动的marker效果。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共76行)安装插件相关API参考:专栏目标示例效果 配置方式 1)查看基础设置…...

关于Dataset和DataLoader的概念
关于Dataset和DataLoader的概念 在机器学习中,Dataset和DataLoader是两个很重要的概念,它们通常用于训练和测试模型时的数据处理。 Dataset是指用于存储和管理数据的类。在深度学习中,通常将数据存储在Dataset中,并使用Dataset提…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
