动态规划概述
动态规划概述
动态规划的两个要求:
1.最优子结构
例:现有一座10级台阶的楼梯,我们要从下往上走,每次只能跨一步,一步可以往上走1级或者2级台阶,请问一共有多少种解法呢?
| 台阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 走法数 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 |
可以发现,我们都可以通过前两个状态来推出当前状态
**最优子结构:**大问题的(最优)解可以由小问题的(最优)解来推出,在这个问题当中,大问题的f(n)的解可以由小问题f(n-2)和f(n-1)的解推出。注意:在问题拆解过程当中不能无限递归
2.无后效性
未来与过去无关,一旦得到了一个小问题的解,如何得到它的解的过程不会影响到大问题的求解。在上面这个问题种,我们只需要知道f(n-1)和f(n-2)的值,但是怎么得到它的已经不重要了。
动态规划的两个元素:
状态:
求解过程进行到了哪一步,可以理解为一个子问题。
转移:
从一个状态(小问题)的(最优)解推导出另一个状态(大问题)的(最优)解的过程。
最短路I
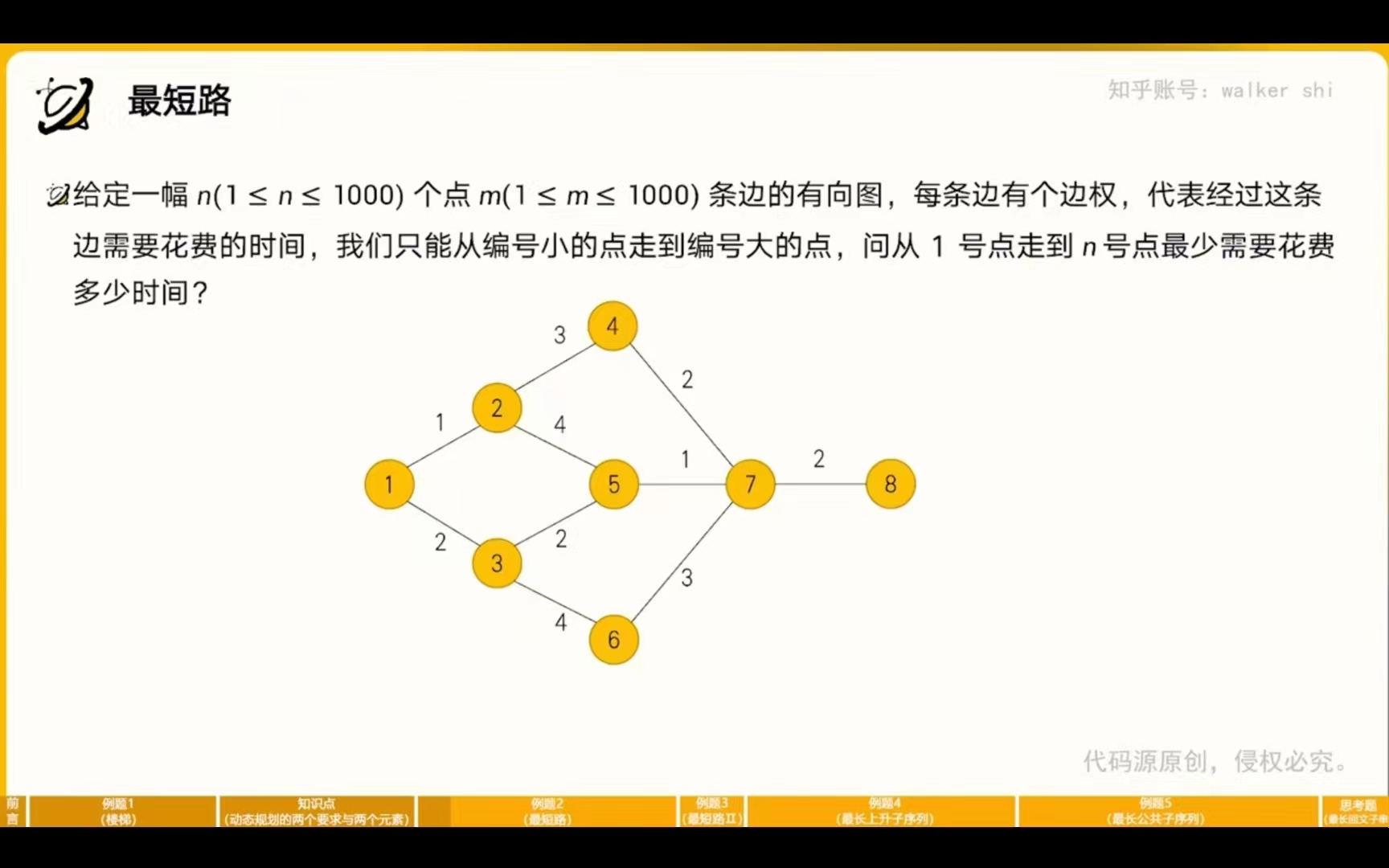
最优子结构:为了计算出从1号点到y号点最少花费的时间,我们可以计算出所有与y号点所连接的边,并且标记所有小于y的点x,从1号点到x号点所花费的最短时间,最后再推到y号点的情况。
无后效性:我们只关心每个点所花费的最短时间,不关心到底是怎么走到这个点的。
状态:f[i]表示从1到i所花费的最短时间
转移:假设已经知道了f[x]的值,并且存在一条从x到y的代价为z的边,那么可以推导出方程:f[y]=min(f[y],f[x]+z)
AC代码:
#include<iostream>
using namespace std;
const int N = 1010;
int a[N][N], f[N], n, m;//a数组存图int main(void)
{cin >> n >> m;memset(a, 127, sizeof(a));//将a的每一条边都初始化为一个很大的值for (int i = 1; i <= m; i++){int x, y, z;cin >> x >> y >> z;a[x][y] = min(a[x][y], z);//防止有重边}memset(f, 127, sizeof f);f[1] = 0;for (int i = 2; i <= n; i++){for (int j = 1; j < i; j++){if (f[j] < 1 << 30 && a[j][i] < 1 << 30)f[i] = min(f[i], f[j] + a[j][i]);}}cout << f[n];return 0;
}
最短路II
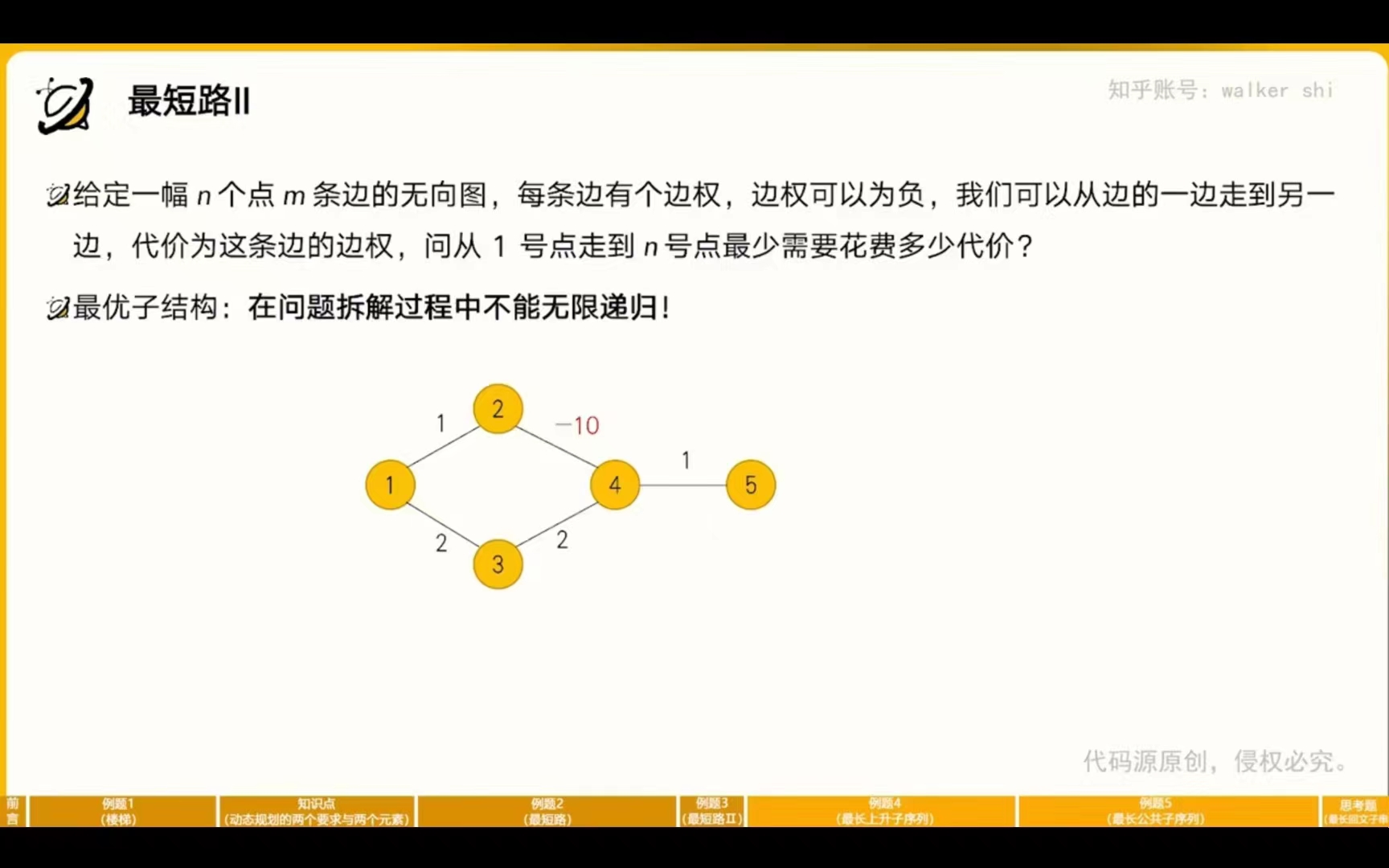
这里存在无限递归,因为每一次绕着1 2 4 3走一圈代价就会减少5,所以不能使用动态规划解决
最长上升子序列

最优子结构:为了计算a[i]以i结尾的最长上升子序列的长度,我们可以通过枚举所有小于i的位置j,我们可以先计算出以a[j]结尾的上升子序列,然后判断a[i]是否大于a[j],如果a[i]>a[j]那么答案就是a[j]+1,反之答案就是a[j]。
无后效性:我们只关心以i这个位置结尾的最长上升子序列的长度,并不关心子序列是什么。
状态:用f[i]表示以i结尾的最长上升子序列的长度
转移:对于某个位置i,为了计算i,我们枚举子序列种所有小于i的元素j,满足j<i&&a[j]<a[i]可以得到状态转移方程:f[i]=max(f[i],f[i]+1)。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 13 | 14 | 17 | 12 | 7 | 8 | 19 | 23 | 52 | 11 | 6 | 9 | 15 | 520 | 1314 | 10 |
| f | 1 | 2 | 3 | 1 | 1 | 2 | 3 | 4 | 5 | 3 | 1 | 3 | 4 | 6 | 7 | 4 |
最后答案等于f[i]当中的最大值
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, a[N], f[N];int main(void)
{cin >> n;int res = -10;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i <= n; i++){f[i] = 1;//如果没有找到能够满足子序列的,那么它的f[i]值就是1,需要初始化一下for (int j = 1; j < i; j++){if (a[j] < a[i]){f[i] = max(f[i], f[j] + 1);if (f[i] > res) res = f[i];}}}cout << res;return 0;
}
最长公共子序列

最优子结构:为了计算出a[i]和b[j]的最长公共子序列,可以从a[i-1]和a[j-1]来转移过来。
假如a[i]==a[j]那么我们可以从f[i-1][j-1]+1转移过来,就是考虑a的前i个元素和b的前j个元素
假如a[i]!=a[j]那么可以从f[i-1][j]和f[i][j-1]转移过来,就是考虑a的前i-1个元素和b的前j个元素以及a的前i个元素和b的前j-1个元素。
这时候可能就有人会有疑问,为什么不考虑f[i-1][j-1]的情况呢?
举一个例子:
| a: | A | D | A | B | C | A | B | C | D |
|---|---|---|---|---|---|---|---|---|---|
| i | |||||||||
| b: | D | B | A | B | C | C | D | A | B |
| j |
如上面的这个表格,如果a[i]!=a[j]那么有没有i和j的元素,对前面的子串都是没有影响的。
串a是ADABCA和ADABC与DBABCC去比较都是一样的,所以f[i-1][j-1]的这种情况已经被包含在
f[i-1][j]和f[i][j-1]当中了。
无后续性:我们只在乎最长公共子序列的长度是多少,至于是哪些元素构成的我们并不在乎
状态:f[i][j]表示a以第i个位置结尾和b以第j个位置结尾的最长公共子序列是多少。
转移:如果a[i]==a[j]那么f[i][j]=f[i-1][j-1]+1。
如果a[i]!=a[j]那么f[i][j]max(f[i-1][j],f[i][j-1])
AC代码:
#include<iostream>
using namespace std;
const int N = 1010;
int n, m, a[N], b[N], f[N][N];int main(void)
{cin >> n >> m;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i <= m; i++) cin >> b[i];for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){f[i][j] = max(f[i - 1][j], f[i][j - 1]);if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);}}cout << f[n][m] << endl;return 0;
}
思考题:最长回文子串
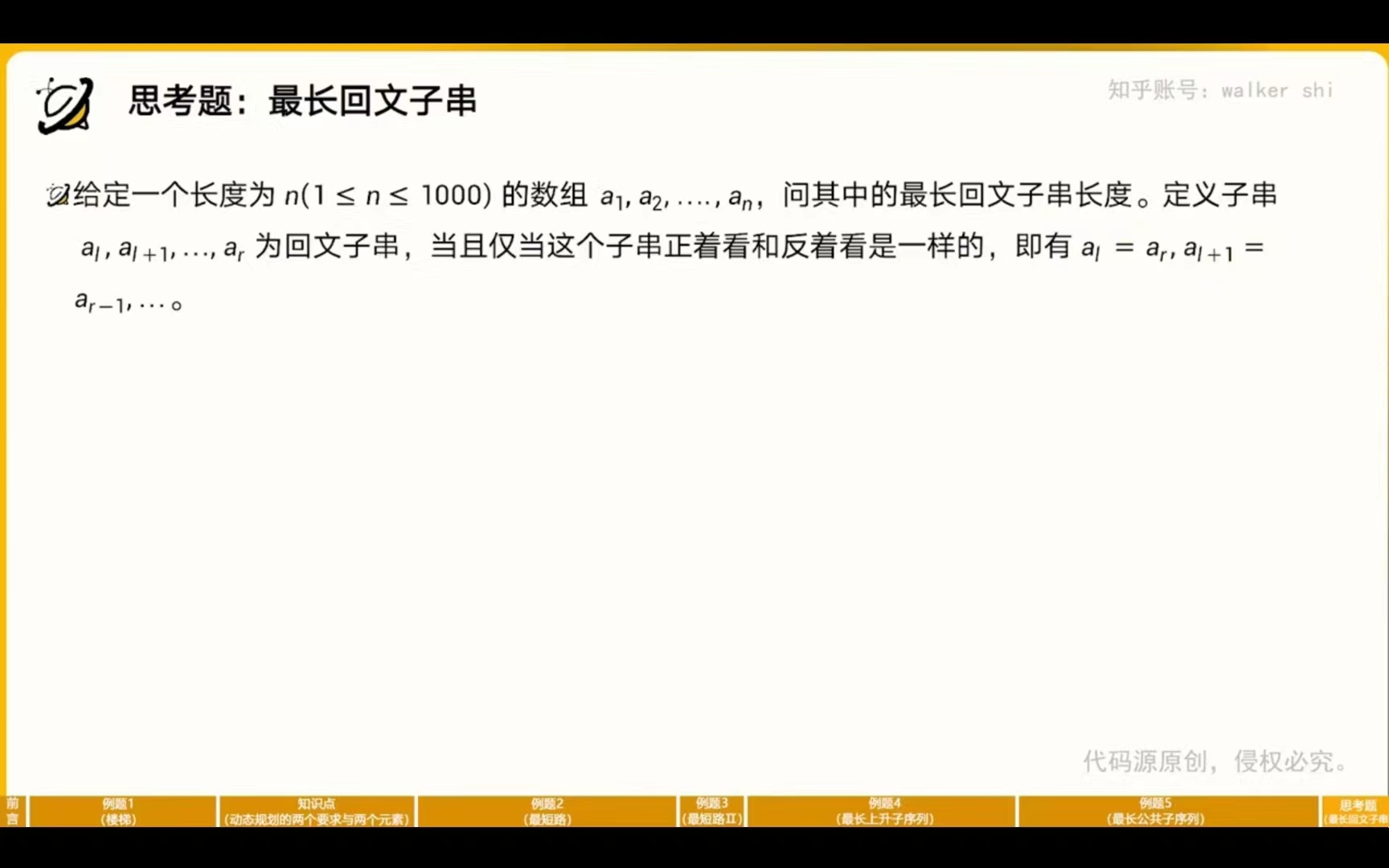
状态:f[i][j]表示从i到j是否满足回文,如果f[i][j]要满足回文字符串的条件,我们可以从
f[i+1][j-1]推到过来,如果f[i+1][j-1]满足回文子串,那么只要str[i==str[j],就可以判定
f[i][j]是回文字符串, 那么如何去得到f[i+1][j-1]的状态呢,我们可以通过不断改变字符串的长度,来判断不同长度字符串的所有情况是否满足是回文子串,比如我要看是否存在长度为4的回文字符串,那么就可以先去找长度为2的,最后判断边界是否相等(str[i]==str[j])即可。
转移:如果str[i]==str[j]那么 f[i][j]=f[i+1][j-1],反之f[i][j]=false。
AC代码:
#include<iostream>
using namespace std;
const int N = 1010;bool f[N][N];
int main(void)
{string str;cin >> str;int len = str.size();for (int i = 0; i <= len; i++){f[i][i] = true;//将一个字符的全都初始化为true}int begin = 0,maxlen=-10010;for (int l = 2; l <= len; l++)//从长度为2开始计算状态,找到满足回文的子串{for (int i = 0; i < len; i++){int j = l + i - 1;if (j >= len) break;if (str[i] != str[j]) f[i][j] = false;else{if (j - i < 3){f[i][j] = true;}else{f[i][j] = f[i + 1][j - 1];}}if (f[i][j] && j - i + 1 > maxlen){maxlen = j - i + 1;begin = i;}}}cout << str.substr(begin, maxlen);return 0;
}
相关文章:

动态规划概述
动态规划概述动态规划的两个要求: 1.最优子结构 例:现有一座10级台阶的楼梯,我们要从下往上走,每次只能跨一步,一步可以往上走1级或者2级台阶,请问一共有多少种解法呢? 台阶数12345678910走法数…...

CPU缓存架构+Disruptor内存队列
文章目录CPU缓存架构Disruptor内存队列CPU缓存架构介绍缓存一致性问题缓存一致性协议MESI协议伪共享问题高性能内存队列DisruptorCPU缓存架构Disruptor内存队列 CPU缓存架构 介绍 cpu与内存的交互数据之间,有一个高速缓存层。有些处理器有3层缓冲,有些…...
Spark SQL join操作详解
一、 数据准备 本文主要介绍 Spark SQL 的多表连接,需要预先准备测试数据。分别创建员工和部门的 Datafame,并注册为临时视图,代码如下: val spark SparkSession.builder().appName("aggregations").master("lo…...
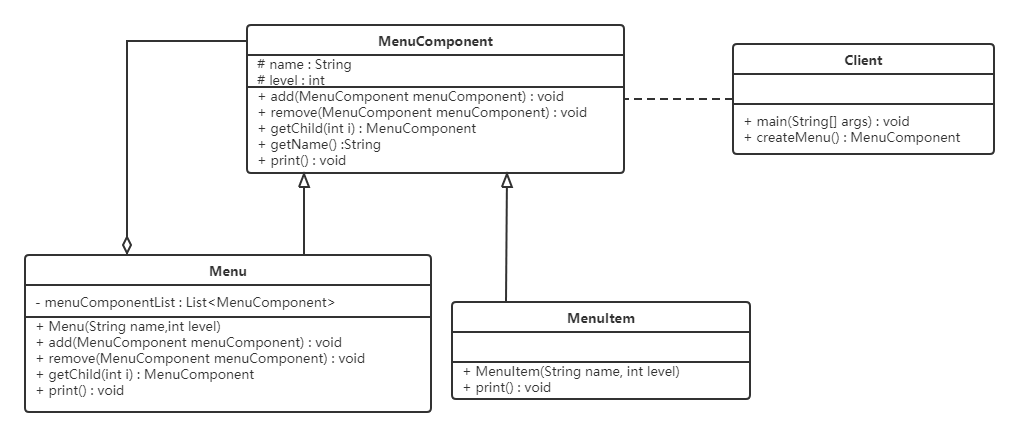
设计模式-day04
5,结构型模式 5.6 组合模式 5.6.1 概述 对于这个图片肯定会非常熟悉,上图我们可以看做是一个文件系统,对于这样的结构我们称之为树形结构。在树形结构中可以通过调用某个方法来遍历整个树,当我们找到某个叶子节点后,…...
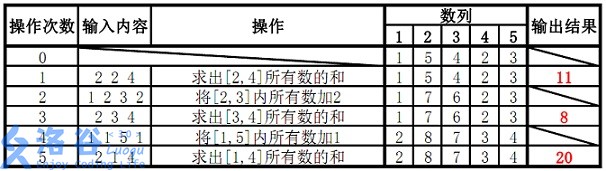
线段树的学习(2023.4.5)
今天我来学习线段树 首先它是树有着树的结构,线段树由于本身是专门用来处理区间问题的 它的作用可以处理区间的问题拥有更快的速度. 对于每一个子节点而言,都表示整个序列中的一段子区间;对于每个叶子节点而言,都表示序列中的单个元素信息…...
Java 实现excel、word、txt、ppt等办公文件在线预览功能
相信大家在开发的过程中都会遇到在线预览功能,有没有想过如何通过java来实现excel、word、txt、ppt等办公文件在线预览功能?今天我们就来解决这一疑问! 其实,网上还是有些公司对这一功能提供了收费服务。那么,如何实现…...

《Vue3实战》 第九章 路由
1、安装路由 cnpm install vue-router42、router-link应用 2.1、创建views/OrderList.vue组件 <template> <h1>订单列表页面......</h1> </template> <script> export default{name: OrderList,data(){return{arr:[4,2,5]} } …...

ToBeWritten之物联网Zigbee协议
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...

【万象奥科】RZ/G2UL网关内存压力测试
测试目的 内存压力测试的目的是测试系统内存的稳定性和可靠性,以便确定系统是否能够在各种负载情况下正常运行。其主要目的有: 测试内存的正确性:通过模拟各种内存负载情况,例如写入随机数据、重复写入相同数据、使用指定的模式…...
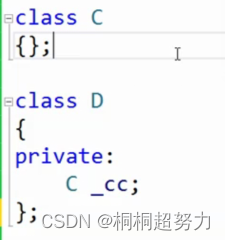
C++中的继承
面向对象的三大特性 封装继承多态 继承的概念和定义 继承的本质就是类层次的复用。 继承的概念继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段.它允许程序员在保持原有类特性的基础上进行扩展,增加功能,这样产生新的类…...
SpringRetry接口异常优雅重试机制
场景: 某些场景下,如果接口出现异常需要进行重试,例如网络抖动、调用接口超时等并非接口代码导致的报错,此时可以进行接口重试机制 1、导入 spring retry 重试依赖 <!-- spring retry --><dependency><groupId>…...

2023年全国最新高校辅导员精选真题及答案46
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 27.充沛的精力和顽强的毅力是教师意志品质的体现。 答案:正确 28.规范与约束…...

程序员为了女朋you进了华为,同学去了阿里,2年后对比收入懵了
什么样的工作才是好工作?每当遇到这个问题,我们的答案总是出奇的一致:钱多事少离家近。 然而现实总是残酷的,日前,有网友在某社交论坛发帖称:自己为了女朋友留在了成都进入华为工作,而自己的同…...
Linux中的算法分离手段
0. 简介 参数分离对于绝大多数算法开发来说收益是非常大的,因为我们都知道,随着平台的更替,很多时候如果说数据流和算法交叠在一起(即接口与实现合在一起)。这将有可能会导致在迁移平台时候会导致代码难以维护&#x…...
机器学习实战:Python基于Logistic逻辑回归进行分类预测
目录1 前言1.1 Logistic回归的介绍1.2 Logistic回归的应用2 iris数据集数据处理2.1 导入函数2.2 导入数据2.3 简单数据查看3 可视化3.1 条形图/散点图3.2 箱线图3.3 三维散点图4 建模预测4.1 二分类预测4.2 多分类预测5 讨论1 前言 1.1 Logistic回归的介绍 逻辑回归ÿ…...
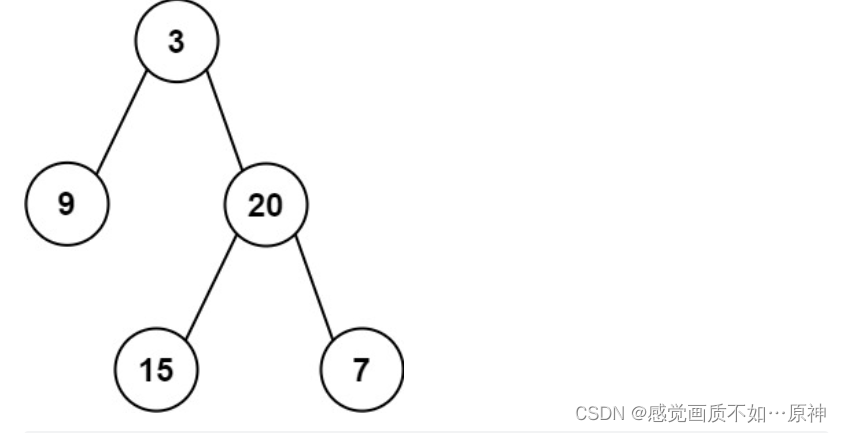
Leetcode.404 左叶子之和
题目链接 Leetcode.404 左叶子之和 easy 题目描述 给定二叉树的根节点 root,返回所有 左叶子 之和。 示例 1: 输入: root [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以…...

Android 11.0 原生SystemUI下拉通知栏UI背景设置为圆角背景的定制(二)
1.前言 在11.0的系统rom定制化开发中,在原生系统SystemUI下拉状态栏的下拉通知栏的背景默认是白色四角的背景, 由于在产品设计中,在对下拉通知栏通知的背景需要把四角背景默认改成圆角背景,所以就需要分析系统原生下拉通知栏的每条通知的默认背景, 然后通过systemui的通知…...

C语言CRC-16 IBM格式校验函数
C语言CRC-16 IBM格式校验函数 CRC-16校验产生2个字节长度的数据校验码,通过计算得到的校验码和获得的校验码比较,用于验证获得的数据的正确性。基本的CRC-16校验算法实现,参考: C语言标准CRC-16校验函数。 不同厂家通过对输入数…...
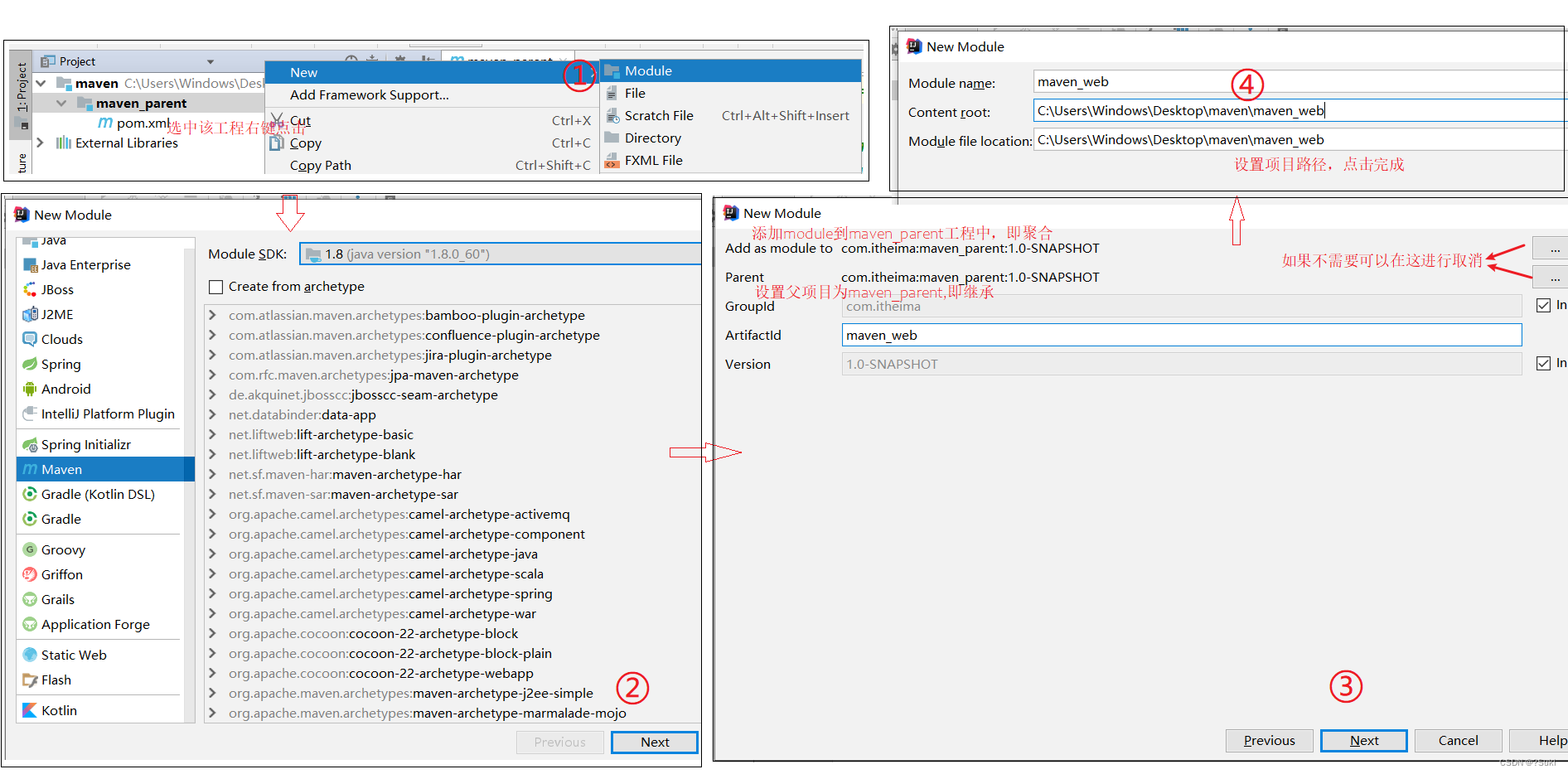
Maven高级-聚合和继承
Maven高级-聚合和继承3,聚合和继承3.1 聚合步骤1:创建一个空的maven项目步骤2:将项目的打包方式改为pom步骤3:pom.xml添加所要管理的项目步骤4:使用聚合统一管理项目3.2 继承步骤1:创建一个空的Maven项目并将其打包方式设置为pom步骤2:在子项目中设置其父工程步骤3:…...

如何写出10万+ Facebook 贴文?
想要创作一篇优秀的Facebook贴文,首先要考虑以下几个问题: 1.文案特点 一篇清晰简洁的文案有助于受众在有限的浏览时间内快速了解你想要展示的信息。根据以往经验,文案内容最好保持在20个汉字以内,加上链接描述最好也不要超过50…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...

使用homeassistant 插件将tasmota 接入到米家
我写一个一个 将本地tasmoat的的设备同通过ha集成到小爱同学的功能,利用了巴法接入小爱的功能,将本地mqtt转发给巴法以实现小爱控制的功能,前提条件。1需要tasmota 设备, 2.在本地搭建了mqtt服务可, 3.搭建了ha 4.在h…...
