当前位置： 首页 > news >正文

307 Temporary Redirect 解决办法（临时重定向）

news 2026/2/9 5:29:03

背景：java后台服务请求python服务端

java服务报错：Unexpected response status：307

python服务端报错：307 Temporary Redirect

解决：查了好久找不到什么原因，请求路径问题

请求url：http//:www.aaaa.com/ack/butter

修改为：http//:www.aaaa.com/ack/butter/

python服务端请求url没有自动在末尾加   /

相关文章：

307 Temporary Redirect 解决办法（临时重定向）

背景：java后台服务请求python服务端 java服务报错：Unexpected response status：307 python服务端报错：307 Temporary Redirect 解决：查了好久找不到什么原因，请求路径问题 请求url：http//:w…...

编程日记 2023/4/13 10:06:58

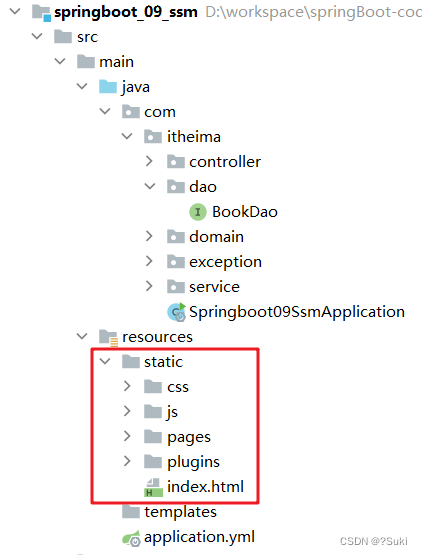
SpringBoot案例

SpringBoot案例5，案例5.1 创建工程5.2 代码拷贝5.3 配置文件5.4 静态资源目标 基于SpringBoot的完成SSM整合项目开发 5，案例 SpringBoot 到这就已经学习完毕，接下来我们将学习 SSM 时做的三大框架整合的案例用 SpringBoot 来实现一下。我们完…...

编程日记 2023/4/13 10:01:57

Android 10.0 系统framework发送悬浮通知的流程分析

1.前言 在android10.0rom定制化开发中,在原生系统的systemui中，状态栏通知，和闹钟，wifi等悬浮通知也是很重要的， 悬浮通知也是系统通知的一种，也是在frameworks中发送出来的通知，接下来就分析下10.0中的悬浮通知的发送 流程，然后就可以实现自己自定义悬浮通知的相关功…...

编程日记 2023/4/13 9:56:56

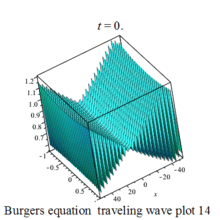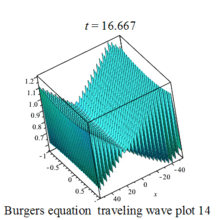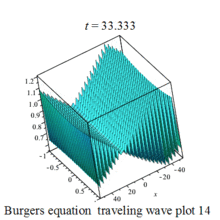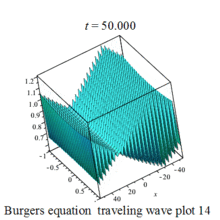
傅里叶谱方法-傅里叶谱方法求解二维浅水方程组和二维粘性 Burgers 方程及其Matlab程序实现

3.3.2 二维浅水方程组 二维浅水方程组是描述水波运动的基本方程之一。它主要用于描述近岸浅水区域内的波浪、潮汐等水动力学现象。这个方程组由两个偏微分方程组成，一个是质量守恒方程，另一个是动量守恒方程。浅水方程描述了具有自由表面、密度均匀、深…...

编程日记 2023/4/13 9:51:55

算法训练营 - 广度优先BFS

目录 从层序遍历开始 N 叉树的层序遍历 经典BFS最短路模板 经典C queue 数组模拟队列 打印路径 示例1.bfs查找所有连接方块 Cqueue版 数组模拟队列 示例2.从多个位置同时开始BFS 示例3.抽象最短路类（作图关键） 示例4.跨过障碍的最短路 从层序遍历…...

编程日记 2023/4/13 9:46:54

​​​​​​​判断两个字符串是否匹配（1个通配符代表一个字符）

目录 判断两个字符串是否匹配（1个通配符代表一个字符） 程序设计 程序分析...

编程日记 2023/4/13 9:41:53

用css画一个csdn程序猿

效果如下&#xff1a; 头部 我们先来拆解一下&#xff0c;程序猿的结构 两只耳朵和头是圆形组成的&#xff0c;耳朵内的红色部分也是圆形 先画头部&#xff0c;利用圆角实现头部形状 借助工具来快速实现圆角效果 https://9elements.github.io/fancy-border-radius/ <div…...

编程日记 2023/4/13 9:36:52

Java多线程编程—wait/notify机制

文章目录1. 不使用wait/notify机制通信的缺点2. 什么是wait/notify机制3. wait/notify机制原理4. wait/notify方法的基本用法5. 线程状态的切换6. interrupt()遇到方法wait()7. notify/notifyAll方法8. wait(long)介绍9. 生产者/消费者模式10. 管道机制11. 利用wait/notify实现…...

编程日记 2023/4/13 9:31:51

Three.js教程：旋转动画、requestAnimationFrame周期性渲染

推荐&#xff1a;将NSDT场景编辑器加入你3D工具链其他工具系列&#xff1a;NSDT简石数字孪生基于WebGL技术开发在线游戏、商品展示、室内漫游往往都会涉及到动画&#xff0c;初步了解three.js可以做什么&#xff0c;深入讲解three.js动画之前&#xff0c;本节课先制作一个简单的…...

编程日记 2023/4/13 9:26:50

租车自驾app开发有什么作用?租车便利出行APP开发

在线租车APP有哪些优势&#xff0c;租车APP开发的基本功能&#xff0c;租车自驾app开发有什么作用?租车便利出行APP开发&#xff0c;租车服务平台小程序有哪些功能&#xff0c;租车软件开发需要多少钱&#xff0c;租车app都有哪些&#xff0c;租车平台定制开发&#xff0c;租车…...

编程日记 2023/4/13 9:21:48

linux shell 文件分割

split 按照 10m 大小进行分割 split -b 10m large_file.bin new_file_prefix...

编程日记 2023/4/13 9:16:46

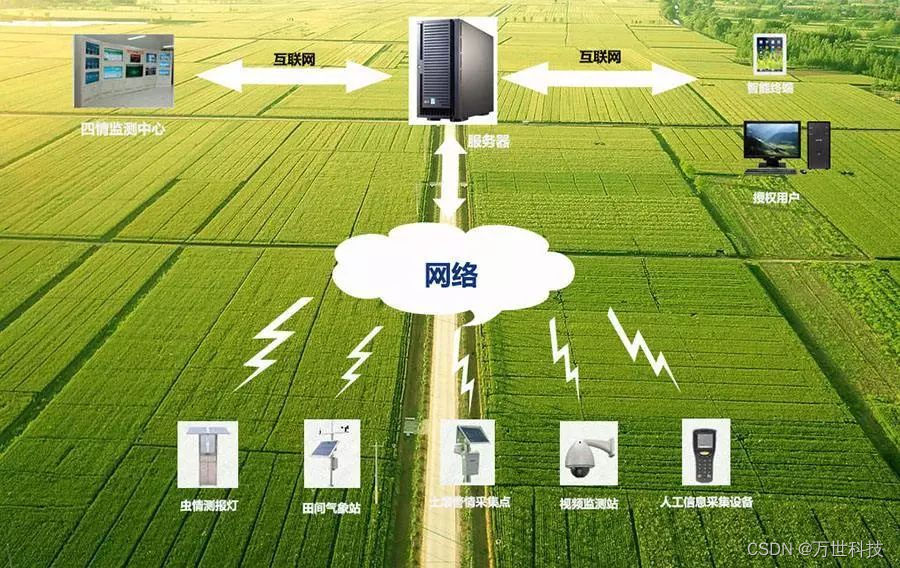
智慧农业系统开发功能有哪些？

农业从古至今都是备受关注的话题&#xff0c;新时代背景下农业发展已经融合了互联网&#xff0c;数字化技术等新型发展方式&#xff0c;形成了农业物联网管控系统&#xff0c;让农业生产更加科技化、智能化、高效化&#xff0c;对农业可持续发展有巨大的推动作用。所以&#xf…...

编程日记 2023/4/13 9:11:45

【C语言】 指针的进阶 看这一篇就够了

目录 1.字符指针 2.数组指针 3.指针数组 4.数组传参和指针传参 5.函数指针 6.函数指针数组 7.指向函数指针数组的指针 8.回调函数 9.qsort排序和冒泡排序 1.字符指针 让我们一起来回顾一下指针的概念&#xff01; 1.指针就是一个变量&#xff0c;用来存放地址&#xff0c;地址…...

编程日记 2023/4/13 9:06:44

redis set list

Listlist: 插入命令&#xff1a;lpush / rpush 查看list列表所有数据(-1 表示最后一个)&#xff1a;lrange key 0 -1 查看列表长度(key 不存在则长度返回0 ): llen key list长度 获取下表 为 0 的元素 修改下标为0的元素&#xff0c;改为haha 移除列表的第一个元素 或最后一…...

编程日记 2023/4/13 9:01:43

如何解决DNS劫持

随着互联网的不断发展&#xff0c;DNS(域名系统)成为了构建网络基础的重要组成部分。而DNS遭到劫持&#xff0c;成为一种常见的安全问题。那么DNS遭到劫持是什么意思呢?如何解决DNS劫持问题呢?下面就让小编来为您一一解答。 DNS遭到劫持是什么意思? DNS遭到劫持指的是黑客通…...

编程日记 2023/4/13 8:56:41

【LeetCode】剑指 Offer（28）

目录 题目&#xff1a;剑指 Offer 54. 二叉搜索树的第k大节点 - 力扣&#xff08;Leetcode&#xff09; 题目的接口&#xff1a; 解题思路&#xff1a; 代码&#xff1a; 过啦&#xff01;&#xff01;&#xff01; 题目&#xff1a;剑指 Offer 55 - I. 二叉树的深度 - 力…...

编程日记 2023/4/13 8:51:41

「ML 实践篇」模型训练

在训练不同机器学习算法模型时&#xff0c;遇到的各类训练算法大多对用户都是一个黑匣子&#xff0c;而理解它们实际怎么工作&#xff0c;对用户是很有帮助的&#xff1b; 快速定位到合适的模型与正确的训练算法&#xff0c;找到一套适当的超参数等&#xff1b;更高效的执行错…...

编程日记 2023/4/13 8:46:40

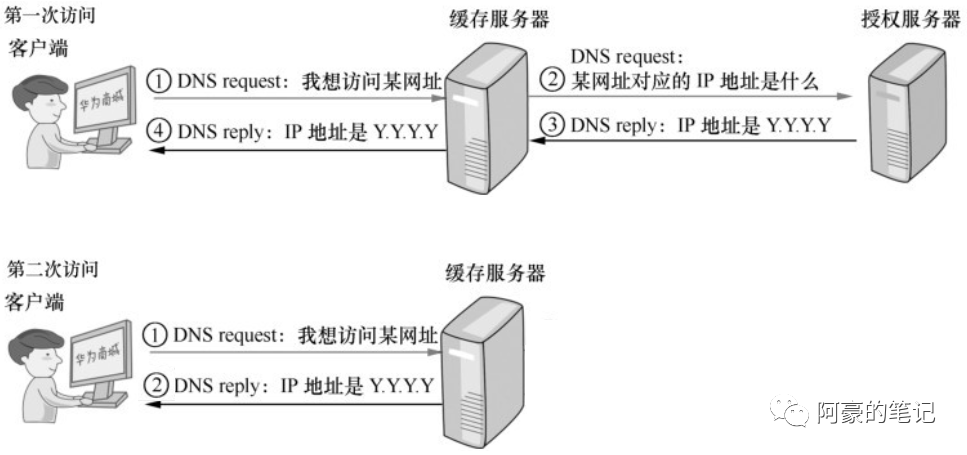
域名解析协议-DNS

DNS&#xff08;Domain Name System&#xff09;是互联网上非常重要的一项服务&#xff0c;我们每天上网都要依靠大量的DNS服务。在Internet上&#xff0c;用户更容易记住的是域名&#xff0c;但是网络中的计算机的互相访问是通过 IP 地址实现的。DNS 最常用的功能是给用户提供…...

编程日记 2023/4/13 8:41:39

分享：包括 AI 绘画在内的超齐全免费可用的API 大全

AI 绘画已经火出圈了&#xff0c;你还不知道哪里可以用嘛&#xff1f;我给大家整理了超级齐全的免费可用 API&#xff0c;包括 AI 绘画在内&#xff0c;有需要的小伙伴赶紧收藏了。 AI 绘画/AI 作画 类 AI 绘画&#xff1a;通过AI 生成图片&#xff0c;包括图生文、文生图等。…...

编程日记 2023/4/13 8:36:38

虹科新闻 | 虹科与Overland-Tandberg正式建立合作伙伴关系

虹科Overland-Tandberg 近日&#xff0c;虹科与美国Overland-Tandberg公司达成战略合作&#xff0c;虹科正式成为Overland-Tandberg公司在中国区域的认证授权代理商。未来&#xff0c;虹科将携手Overland-Tandberg&#xff0c;共同致力于提供企业数据管理和保护解决方案。 虹科…...

编程日记 2023/4/13 8:31:36

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

编程新知 2026/1/26 21:57:45

dedecms 织梦自定义表单留言增加ajax验证码功能

增加ajax功能模块&#xff0c;用户不点击提交按钮&#xff0c;只要输入框失去焦点&#xff0c;就会提前提示验证码是否正确。 一&#xff0c;模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

编程新知 2026/2/5 17:51:52

Nginx server_name 配置说明

Nginx 是一个高性能的反向代理和负载均衡服务器&#xff0c;其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机&#xff08;Virtual Host&#xff09;。 1. 简介 Nginx 使用 server_name 指令来确定…...

编程新知 2025/9/6 16:47:17

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现，论文初版实现

摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序&#xff0c;以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务&#xff0c;提供稳定高效的数据处理与业务逻辑支持&#xff1b;利用 uniapp 实现跨平台前…...

编程新知 2026/1/31 10:55:22

聊一聊接口测试的意义有哪些？

目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开&#xff0c;首…...

编程新知 2025/10/14 6:46:13

初学 pytest 记录

安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

编程新知 2026/2/8 21:57:26

ZYNQ学习记录FPGA(一)ZYNQ简介

一、知识准备 1.一些术语,缩写和概念&#xff1a; 1&#xff09;ZYNQ全称&#xff1a;ZYNQ7000 All Pgrammable SoC 2&#xff09;SoC:system on chips(片上系统)&#xff0c;对比集成电路的SoB&#xff08;system on board&#xff09; 3&#xff09;ARM&#xff1a;处理器…...

编程新知 2026/2/5 9:30:45

拟合问题处理

在机器学习中&#xff0c;核心任务通常围绕模型训练和性能提升展开&#xff0c;但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正&#xff1a; 一、机器学习的核心任务框架 机…...

编程新知 2025/9/6 11:47:54

VSCode 没有添加Windows右键菜单

关键字&#xff1a;VSCode&#xff1b;Windows右键菜单&#xff1b;注册表。 文章目录 前言一、工程环境二、配置流程1.右键文件打开2.右键文件夹打开3.右键空白处打开文件夹 三、测试总结 前言 安装 VSCode 时没有注意&#xff0c;实际使用的时候发现 VSCode 在 Windows 菜单栏…...

编程新知 2026/2/8 22:07:37

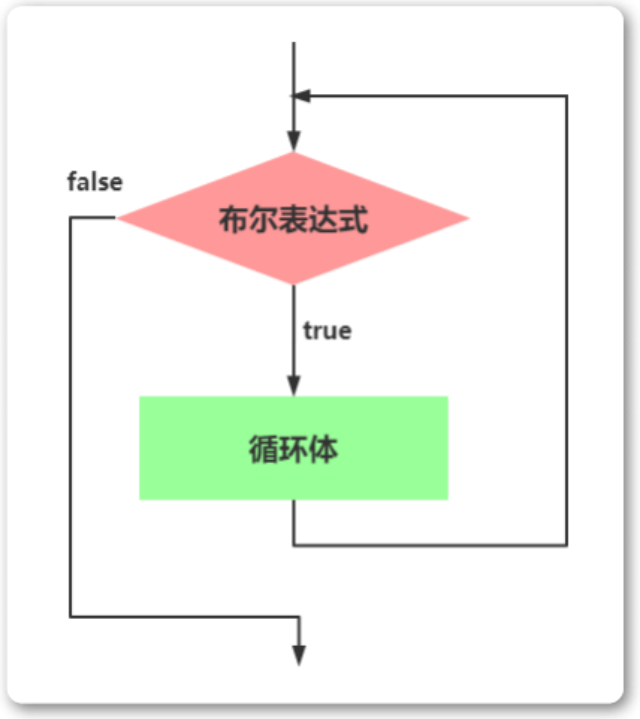
循环语句之while

While语句包括一个循环条件和一段代码块&#xff0c;只要条件为真&#xff0c;就不断 循环执行代码块。 1 2 3 while (条件) { 语句 ; } var i 0; while (i < 100) {console.log(i 当前为&#xff1a; i); i i 1; } 下面的例子是一个无限循环&#xff0c;因…...

编程新知 2026/1/27 2:45:27