当前位置： 首页 > news >正文

FTP-----局域网内部远程桌面

news 2026/2/10 1:50:06

此文包含详细的图文教程。有疑问评论区留言。博主第一时间解决。 

目录

一、被远程桌面的电脑

1.开启远程权限

2.添加账户，有本地账户跳过这步

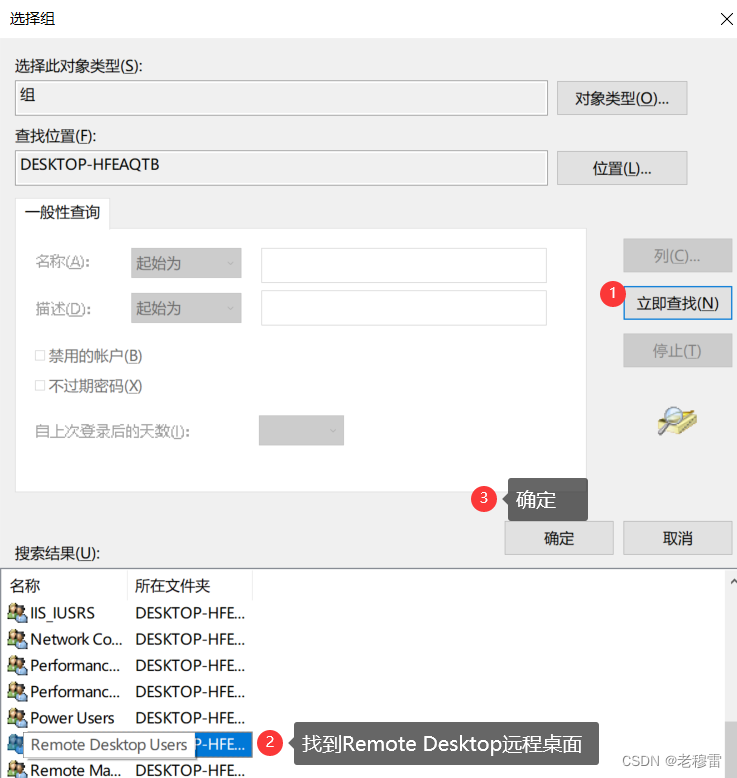
3.帐号隶属于  远程桌面 

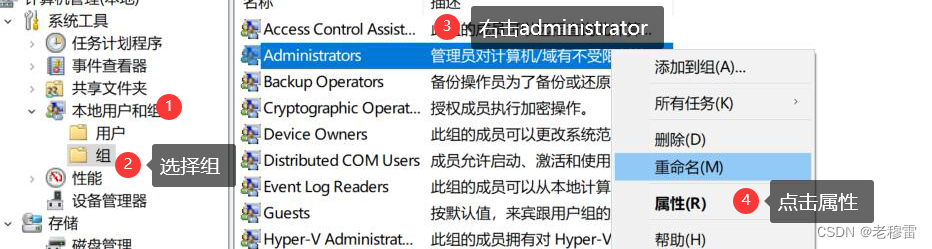
4.帐号隶属于  本地用户组

二、本地电脑连接远程桌面

前提条件：

                  1.两台电脑在同一局域网

                  2.两台电脑Windows版本都是专业版

模拟局域网： 手机开热点，两台电脑连接热点。

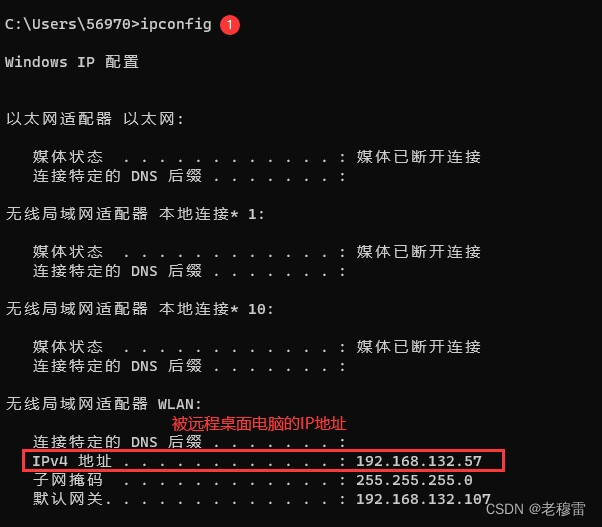
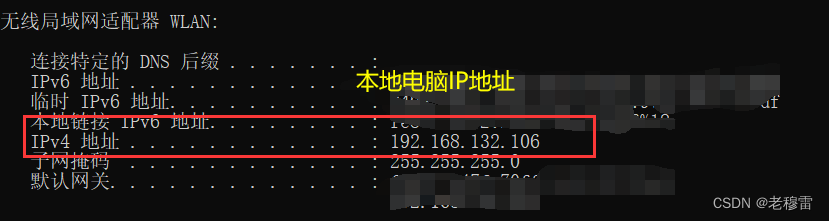
查看两台电脑的IP地址是否在同一网段 

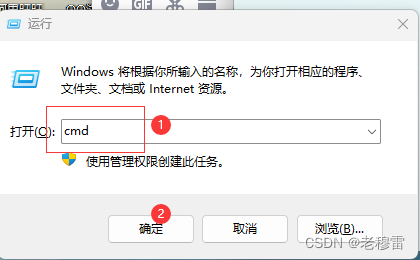
快捷键 win+R键-------输入cmd确认--------输入ipconfig回车

 

专业版才能打开远程桌面、

专业版windows10或者windows11

快捷键 win+R 键-------输入cmd 确认--------输入 wmic os get caption 回车

 

  获取windos专业版点击链接： 家庭版本升级为专业版

                                                        准备完毕，进入正题

一、被远程桌面的电脑

 

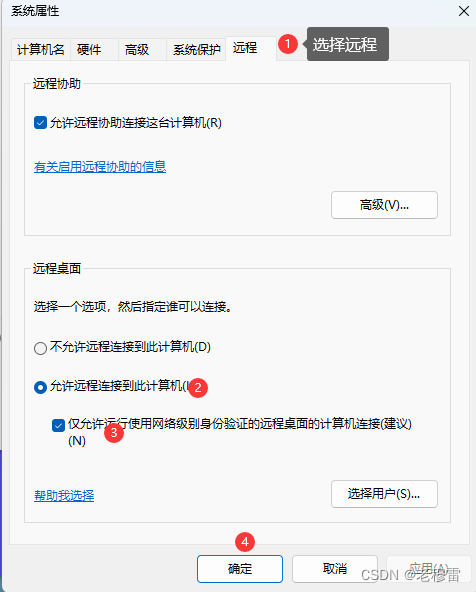
1.开启远程权限

快捷键 win+R 键-------输入 sysdm.cpl 确认

 

 

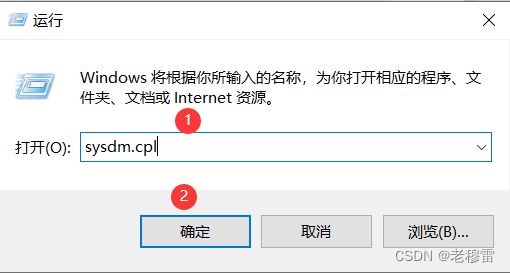
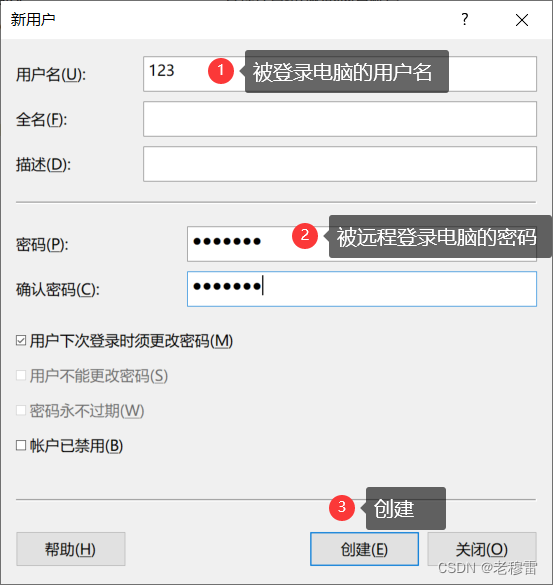
2.添加账户，有本地账户跳过这步

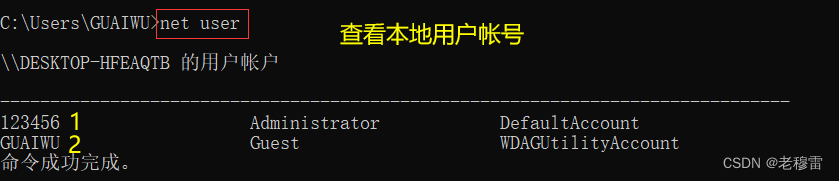
快捷键 win+R 键-------输入cmd 确认-------输入 net user 回车

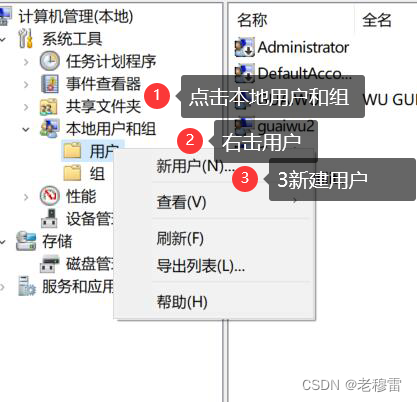
快捷键 win+R 键-------输入 Compmgmt.msc 确认

 

 

3.帐号隶属于  远程桌面 

 

 

 

最后点击 应用或者确定

 

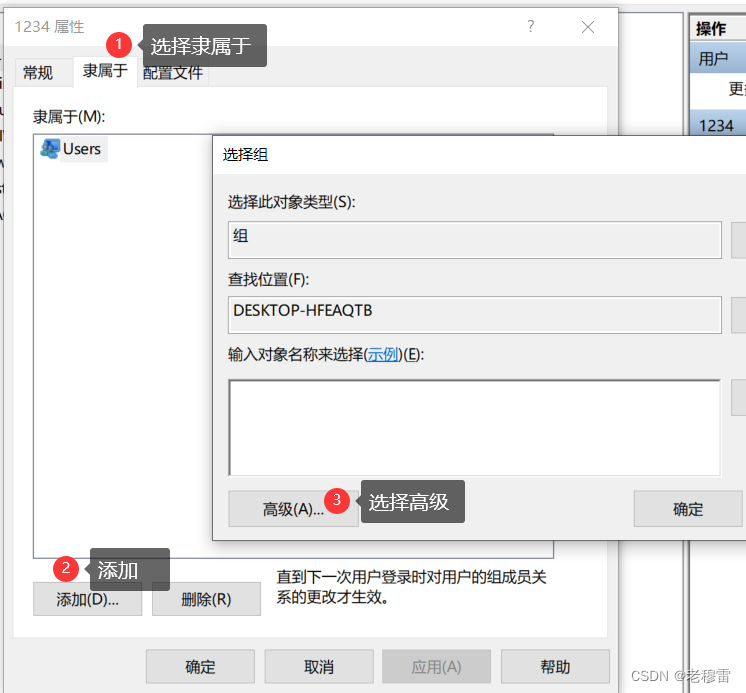
4.帐号隶属于  本地用户组

最后点击  应用或者确定

 

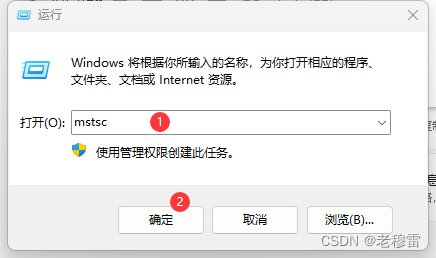
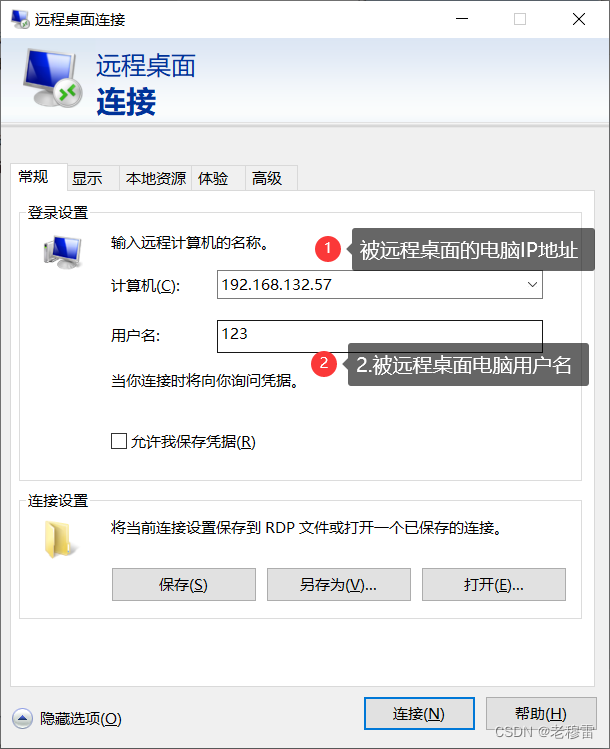
二、本地电脑连接远程桌面

 

快捷键 win+R键-------输入 mstsc 确认

 

参考资料：1.远程桌面提示要远程登录，你需要具有通过远程桌面服务进行登录的权限

                  2.远程桌面没有授权此用户账户进行远程登录怎么办？

                  3.windows开启远程桌面_哔哩哔哩_bilibili

相关文章：

FTP-----局域网内部远程桌面

此文包含详细的图文教程。有疑问评论区留言。博主第一时间解决。 目录 一、被远程桌面的电脑 1.开启远程权限 2.添加账户，有本地账户跳过这步 3.帐号隶属于 远程桌面 4.帐号隶属于 本地用户组 二、本地电脑连接远程桌面 前提条件： 1.两台电脑在…...

编程日记 2023/4/13 11:37:20

Learning C++ No.18【STL No.8】

引言： 北京时间：2023/3/18/21:47，周末，不摆烂，但是欠钱终于还是遭报应了，导致坐牢7小时（上午3.5，下午3.5），难受，充分意识到行哥是那么的和蔼可亲…...

编程日记 2023/4/13 11:32:19

pytorch搭建ResNet50实现鸟类识别

🍨 本文为🔗365天深度学习训练营 中的学习记录博客 🍦 参考文章地址： 365天深度学习训练营-第J1周：ResNet-50算法实战与解析 🍖 作者：K同学啊 理论知识储备 深度残差网络ResNet（dee…...

编程日记 2023/4/13 11:27:18

Node.js -- npm与包

1.包 Node.js中的第三方模块又叫做包 就像电脑和计算机指的是相同的东西，第三方模块和包指的是同一概念，只不过叫法不同。 包的来源： 包是由第三方或者个人团队开发出来的，免费供个人使用。 国外有一家IT 公司，叫做n…...

编程日记 2023/4/13 11:22:17

二 、Locust自定义用户（场景)

二 、自定义用户（场景） 一个用户类代表了你系统中的一种用户/场景。当你做一个测试运行时，你指定你想模拟的并发用户的数量，Locust将为每个用户创建一个实例。你可以给这些类/实例添加任何你喜欢的属性，但有一些属性对…...

编程日记 2023/4/13 11:17:15

1~3年的测试工程师薪资陷入了瓶颈期，如何突破自己实现涨薪？

对于技术人员而言，职业规划一般分为两个方向：做技术、做管理。进入软件测试行业的新人都会从最基础的执行开始，然后是基本的功能测试。 随后大家会根据个人职业发展来进一步细化，有的走管理路线，成为主管、经理、项目…...

编程日记 2023/4/13 11:12:14

springboot项目前端ajax 07进阶优化，使用jQuery的ajax

使用官网https://jquery.com/ 在下载那里，选择Download the compressed, production jQuery 3.6.4（版本不一样），而后在打开的网页中，选择另存为，就下载好了js文件。 > function doAjax(){ …...

编程日记 2023/4/13 11:07:13

东数西存场景的探索与实践

“东数西算”是通过构建数据中心、云计算、大数据一体化的新型算力网络体系，将东部算力需求有序引导到西部，对优化数据中心建设布局，提升国家整体算力水平，促进绿色发展，扩大有效投资，具有重要意义。 在实…...

编程日记 2023/4/13 11:02:12

[图神经网络]PyTorch简单实现一个GCN

Pytorch自带一个PyG的图神经网络库，和构建卷积神经网络类似。不同于卷积神经网络仅需重构__init__( )和forward( )两个函数，PyTorch必须额外重构propagate( )和message( )函数。 一、环境构建 ①安装torch_geometric包。 pip install torch_geometric …...

编程日记 2023/4/13 10:57:10

Elasticsearch(黑马)

初识elasticsearch ​​. 安装elasticsearch 1.部署单点es 1.1.创建网络 因为我们还需要部署kibana容器，因此需要让es和kibana容器互联。这里先创建一个网络： docker network create es-net 1.2.加载镜像 这里我们采用elasticsearch的7.12.1版本的…...

编程日记 2023/4/13 10:52:09

oracle数据库调整字段类型

oracle数据库更改字段类型比较墨迹，因为如果该字段有值，是不允许直接更改字段类型的。另外oralce不支持在指定的某个字段后面新增一个字段，但是mysql数据可以向指定的字段后面新增一个字段。 mysql向指定字段后面新增一个字段： al…...

编程日记 2023/4/13 10:47:07

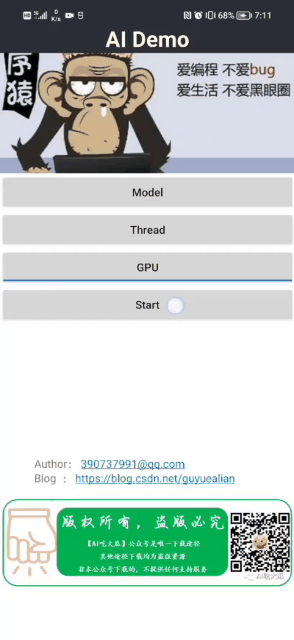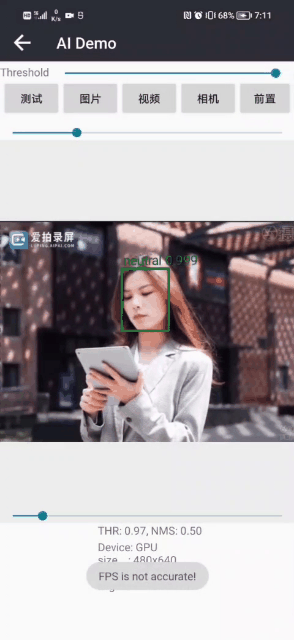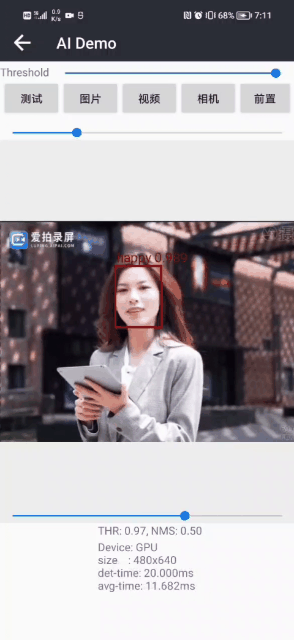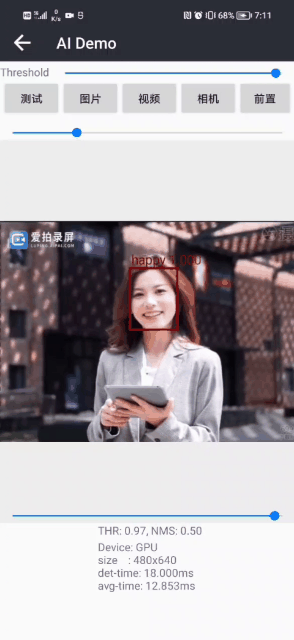
面部表情识别2：Pytorch实现表情识别(含表情识别数据集和训练代码)

面部表情识别2：Pytorch实现表情识别(含表情识别数据集和训练代码) 目录 面部表情识别2：Pytorch实现表情识别(含表情识别数据集和训练代码) 1.面部表情识别方法 2.面部表情识别数据集 （1）表情识别数据集说明 （2&…...

编程日记 2023/4/13 10:42:06

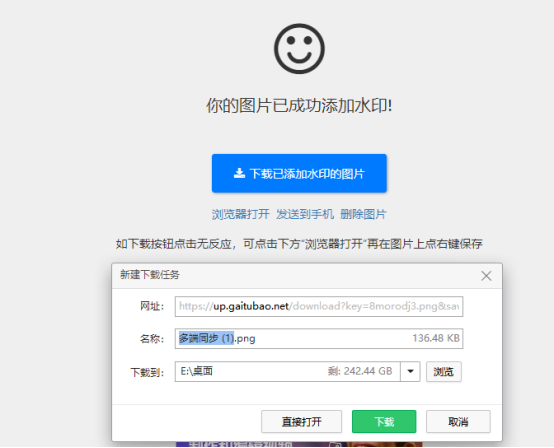
赛效：如何在线给图片加水印

学会给图片加水印是一个非常实用的技能，可以让你的图片更具保护性和个性化。说到加水印，很多人不知道怎么操作。其实，给图片加水印非常简单，不用下载任何程序，在线就能完成。今天，我将介绍如何使用改图宝在…...

编程日记 2023/4/13 10:37:05

动力节点杜老师Vue笔记——Vue程序初体验

一、Vue程序初体验 我们可以先不去了解Vue框架的发展历史、Vue框架有什么特点、Vue是谁开发的，这些对我们编写Vue程序起不到太大的作用，更何况现在说了一些特点之后，我们也没有办法彻底理解它，因此我们可以先学会用，使…...

编程日记 2023/4/13 10:32:04

ajax上传图片存入到指定的文件夹并回显

html代码&#xff1a; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><script src"js/jquery-2.1.0.js"></script> </head> <body> <form…...

编程日记 2023/4/13 10:27:03

cesium加载cesiumlab切的影像切片和标准TMS瓦片的区别

1.加载cesiumlab切的影像 var labImg viewer.scene.imageryLayers.addImageryProvider( new Cesium.UrlTemplateImageryProvider({url:http://192.168.1.25:8080/DOMtms/{z}/{x}/{y}.png,fileExtension : "png"})); 2.标准TMS瓦片 var labImg viewer.scene.im…...

编程日记 2023/4/13 10:22:02

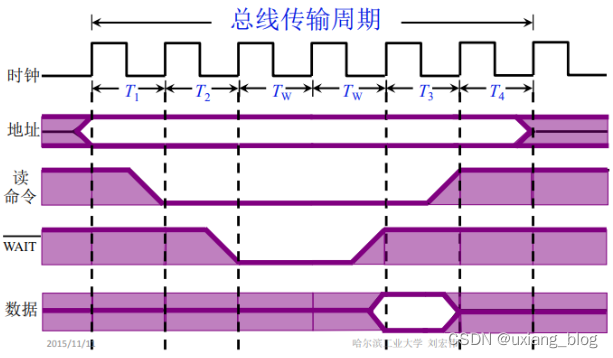
第二周P9-P22

文章目录第三章 系统总线3.1、总线的基本概念一、为什么要用总线二、什么是总线三、总线上信息的传送四、总线结构的计算机举例1、单总线结构框图2、面向CPU的双总线结构框图3、以存储器为中心的双总线结构图3.2、总线的分类1、片内总线2、系统总线3、通信走线3.3、总线特性及性…...

编程日记 2023/4/13 10:17:01

java反射

文章目录何为反射&#xff1f;反射的应用场景了解么&#xff1f;谈谈反射机制的优缺点优点缺点反射实战获取 Class 对象的四种方式1. 知道具体类的情况下可以使用TargetObject.class&#xff1a;2. 通过 Class.forName()传入类的全路径获取&#xff1a;3. 通过对象实例instance…...

编程日记 2023/4/13 10:11:59

307 Temporary Redirect 解决办法（临时重定向）

背景&#xff1a;java后台服务请求python服务端 java服务报错&#xff1a;Unexpected response status&#xff1a;307 python服务端报错&#xff1a;307 Temporary Redirect 解决&#xff1a;查了好久找不到什么原因&#xff0c;请求路径问题 请求url&#xff1a;http//:w…...

编程日记 2023/4/13 10:06:58

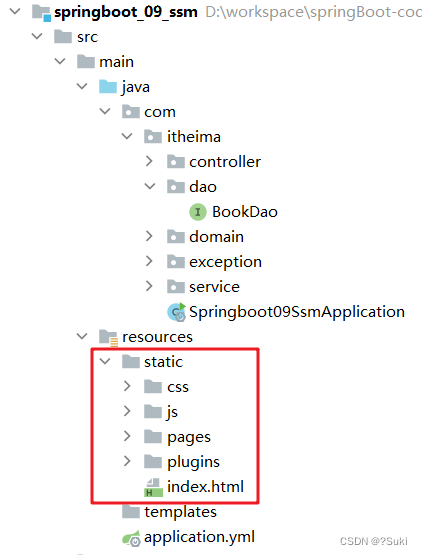
SpringBoot案例

SpringBoot案例5&#xff0c;案例5.1 创建工程5.2 代码拷贝5.3 配置文件5.4 静态资源目标 基于SpringBoot的完成SSM整合项目开发 5&#xff0c;案例 SpringBoot 到这就已经学习完毕&#xff0c;接下来我们将学习 SSM 时做的三大框架整合的案例用 SpringBoot 来实现一下。我们完…...

编程日记 2023/4/13 10:01:57

未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？

编辑&#xff1a;陈萍萍的公主一点人工一点智能 未来机器人的大脑&#xff1a;如何用神经网络模拟器实现更智能的决策&#xff1f;RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战&#xff0c;在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

编程新知 2026/2/7 23:18:28

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

使用VSCode开发Django指南

使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架&#xff0c;专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用&#xff0c;其中包含三个使用通用基本模板的页面。在此…...

编程新知 2026/2/8 16:24:38

基于服务器使用 apt 安装、配置 Nginx

&#x1f9fe; 一、查看可安装的 Nginx 版本 首先&#xff0c;你可以运行以下命令查看可用版本&#xff1a; apt-cache madison nginx-core输出示例&#xff1a; nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2026/1/9 12:53:59

ESP32读取DHT11温湿度数据

芯片&#xff1a;ESP32 环境&#xff1a;Arduino 一、安装DHT11传感器库 红框的库&#xff0c;别安装错了 二、代码 注意&#xff0c;DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

编程新知 2026/1/30 8:46:45

深入理解JavaScript设计模式之单例模式

目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式&#xff08;Singleton Pattern&#…...

编程新知 2026/1/31 17:09:43

零基础设计模式——行为型模式 - 责任链模式

第四部分&#xff1a;行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习&#xff01;行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想&#xff1a;使多个对象都有机会处…...

编程新知 2026/1/31 9:33:18

根据万维钢·精英日课6的内容，使用AI（2025）可以参考以下方法：

根据万维钢精英日课6的内容&#xff0c;使用AI&#xff08;2025&#xff09;可以参考以下方法&#xff1a; 四个洞见 模型已经比人聪明&#xff1a;以ChatGPT o3为代表的AI非常强大&#xff0c;能运用高级理论解释道理、引用最新学术论文&#xff0c;生成对顶尖科学家都有用的…...

编程新知 2026/1/10 1:08:51

JavaScript基础-API 和 Web API

在学习JavaScript的过程中&#xff0c;理解API&#xff08;应用程序接口&#xff09;和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能&#xff0c;使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

编程新知 2025/8/21 23:03:46

【C++特殊工具与技术】优化内存分配(一)：C++中的内存分配

目录 一、C 内存的基本概念​ 1.1 内存的物理与逻辑结构​ 1.2 C 程序的内存区域划分​ 二、栈内存分配​ 2.1 栈内存的特点​ 2.2 栈内存分配示例​ 三、堆内存分配​ 3.1 new和delete操作符​ 4.2 内存泄漏与悬空指针问题​ 4.3 new和delete的重载​ 四、智能指针…...

编程新知 2026/1/31 6:12:22