二叉树的后序遍历(力扣145)
目录
题目描述:
解法一:递归法
解法二:迭代法
解法三:Morris遍历
二叉树的后序遍历
题目描述:
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:

输入:root = [1,null,2,3] 输出:[3,2,1]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
- 树中节点的数目在范围
[0, 100]内 -100 <= Node.val <= 100
解法一:递归法
List<Integer> res = new ArrayList<>();public List<Integer> postorderTraversal(TreeNode root) {if(root == null){return res;}postorderTraversal(root.left);postorderTraversal(root.right);res.add(root.val);return res;}复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
- 空间复杂度:O(n)O(n),为递归过程中栈的开销,平均情况下为 O(\log n)O(logn),最坏情况下树呈现链状,为 O(n)O(n)。
解法二:迭代法
public List<Integer> postorderTraversal1(TreeNode root) {List<Integer> res = new ArrayList<>();if(root == null){return res;}Deque<TreeNode> stack = new ArrayDeque<>();TreeNode cur = root;TreeNode prev = null;while(cur!=null || !stack.isEmpty()){while(cur != null){stack.push(cur);cur = cur.left;}cur = stack.pop();if(cur.right==null || prev==cur.right){res.add(cur.val);prev = cur;cur = null;}else{stack.push(cur);cur = cur.right;}}return res;}复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
- 空间复杂度:O(n)O(n),为迭代过程中显式栈的开销,平均情况下为 O(\log n)O(logn),最坏情况下树呈现链状,为 O(n)O(n)。
解法三:Morris遍历
public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();if (root == null) {return res;}TreeNode p1 = root, p2 = null;while (p1 != null) {p2 = p1.left;if (p2 != null) {while (p2.right != null && p2.right != p1) {p2 = p2.right;}if (p2.right == null) {p2.right = p1;p1 = p1.left;continue;} else {p2.right = null;addPath(res, p1.left);}}p1 = p1.right;}addPath(res, root);return res;}public void addPath(List<Integer> res, TreeNode node) {int count = 0;while (node != null) {++count;res.add(node.val);node = node.right;}int left = res.size() - count, right = res.size() - 1;while (left < right) {int temp = res.get(left);res.set(left, res.get(right));res.set(right, temp);left++;right--;}}复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 是二叉树的节点数。没有左子树的节点只被访问一次,有左子树的节点被访问两次。
- 空间复杂度:O(1)O(1)。只操作已经存在的指针(树的空闲指针),因此只需要常数的额外空间。
相关文章:

二叉树的后序遍历(力扣145)
目录 题目描述: 解法一:递归法 解法二:迭代法 解法三:Morris遍历 二叉树的后序遍历 题目描述: 给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。 示例 1: 输入:root …...

《Effective C++》读书纪实 -- 诸君同享
文章目录《Effective C》是一本经典的C编程指南,共包含50条C编程的最佳实践。 确定你的构造函数的行为 在构造函数中,应该尽可能地避免调用虚函数、非静态成员函数和虚基类的函数。 尽量使用const、enum、inline替换#define 使用const、enum、inline可以…...

【云原生】K8S-ConfigMap 实现应用和配置分离
文章目录前言ConfigMap 背景ConfigMap 创建方式ConfigMap 的使用使用 ConfigMap 的注意事项总结前言 Kubernetes 是目前最流行的容器编排系统之一,它提供了丰富的功能来支持容器化应用程序的管理和部署。 ConfigMap 是 Kubernetes 中重要的资源对象,用…...
)
java -测距工具(经纬度)
代码 /*** 测距工具* author qb*/ public class DistanceUtils {/*** 赤道半径*/private static final double EARTH_RADIUS 6378.137;private static double rad(double d) {return d * Math.PI / 180.0;}/*** Description : 通过经纬度获取距离(单位:米)* Group…...

postgres分区表的创建-基于继承
参考文档: http://postgres.cn/docs/12/ddl-partitioning.html 创建基于继承的分区表的步骤 1 创建父表 2 创建子表,从父表继承过来 3 创建函数及触发器,使插入的数据根据规则,插入到对应的子表中 -- 创建父表 CREATE TABLE a…...
Docker应用部署
文章目录Docker 应用部署一、部署MySQL二、部署Tomcat三、部署Nginx四、部署RedisDocker 应用部署 一、部署MySQL 搜索mysql镜像 docker search mysql拉取mysql镜像 docker pull mysql:5.6创建容器,设置端口映射、目录映射 # 在/root目录下创建mysql目录用于存…...
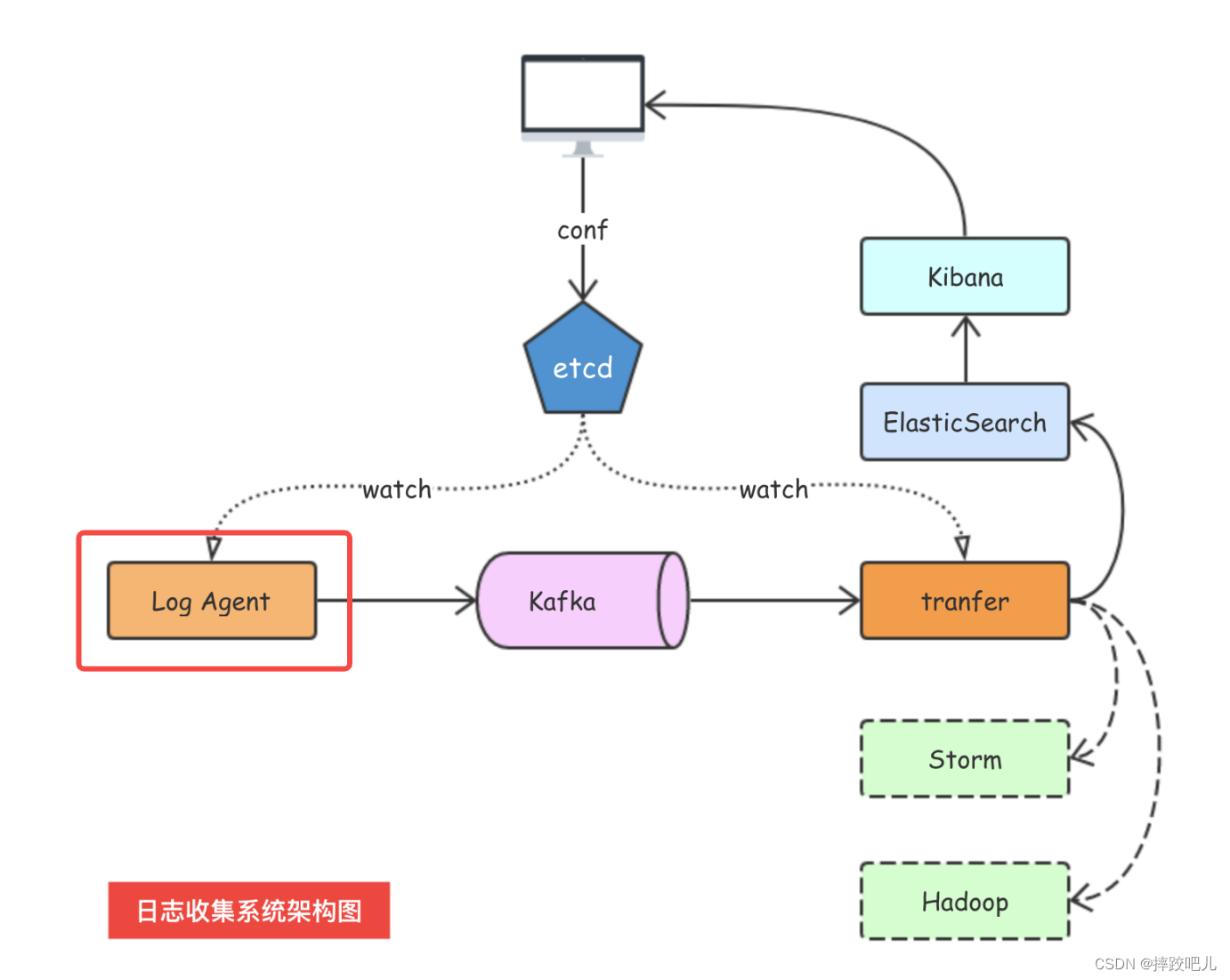
使用golang实现日志收集系统的logagent
整体架构 参考 七米老师的日志收集项目 主要用go实现logagent的部分,logagent的作用主要是实时监控日志追加的变化,并将变化发送到kafka中。 之前我们已经实现了 用go连接kafka并向其中发送数据,也实现了使用tail库监控日志追加操作。 我们…...

小红书点赞不显示怎么回事?小红书笔记评论被吞怎么办
小红书作为一个互联网产品,是一个软件。既然是软件就会有一定的程序漏洞,这是无法避免的。但是很多时候其实并不一定是漏洞的问题。今天就来和大家谈谈小红书点赞不显示怎么回事,小红书评论被吞又是怎么一回事,这些难道都是程序性…...

地址变换和缺页置换习题
1.设某进程页面的访问序列为4,3,2,1,4,3,5,4,3,2,1,5,当分配给该进程的内存页框数分别为3和4时,对于先进先出,最近最少使用,最佳页面置换算法,分别发生多少次缺页中断? 答: 分配的…...
)
PAT 乙级 1010 一元多项式求导(解题思路+AC代码)
题目: 设计函数求一元多项式的导数。(注:xn(n为整数)的一阶导数为nxn−1。) 输入格式: 以指数递降方式输入多项式非零项系数和指数(绝对值均为不超过 1000 的整数)。数字间以空格分…...

一维河流污染持续排放模拟(水污染扩散)
一、处理河道转换为geojson数据 以淮河为例处理示例数据: {"type": "FeatureCollection","features": [{"geometry": {"coordinates": [[[115.5803,34.4982],[115.5922,34.498],[115.6061,34.4994],[115.6203,…...
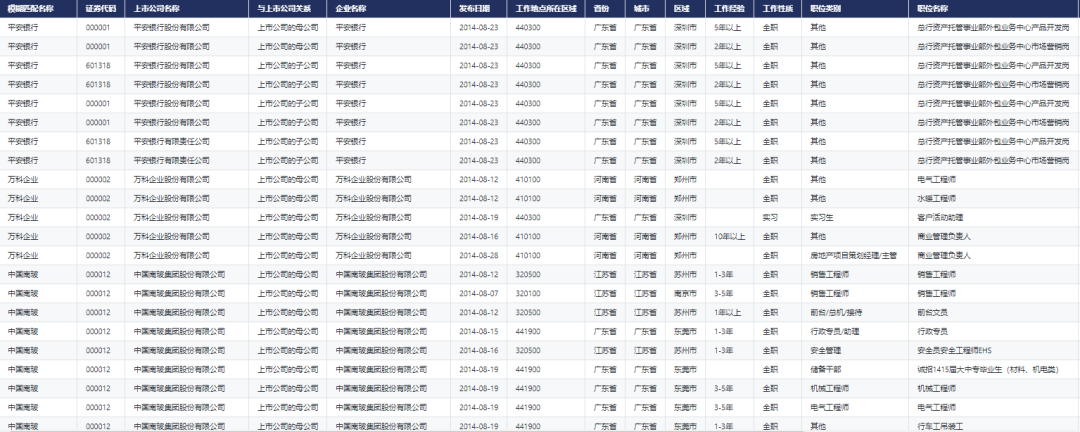
数据优化 | CnOpenDataA股上市公司招聘数据
就业是经济的“晴雨表”,更是社会的“稳定器”。稳定和扩大就业一直是国家宏观调控的重要目标,2021年中央经济工作会议八次提到“就业”这一关键词。在新冠肺炎疫情蔓延、世界经济下行及人口老龄化加快等多重因素的叠加之下,稳就业保民生成为…...
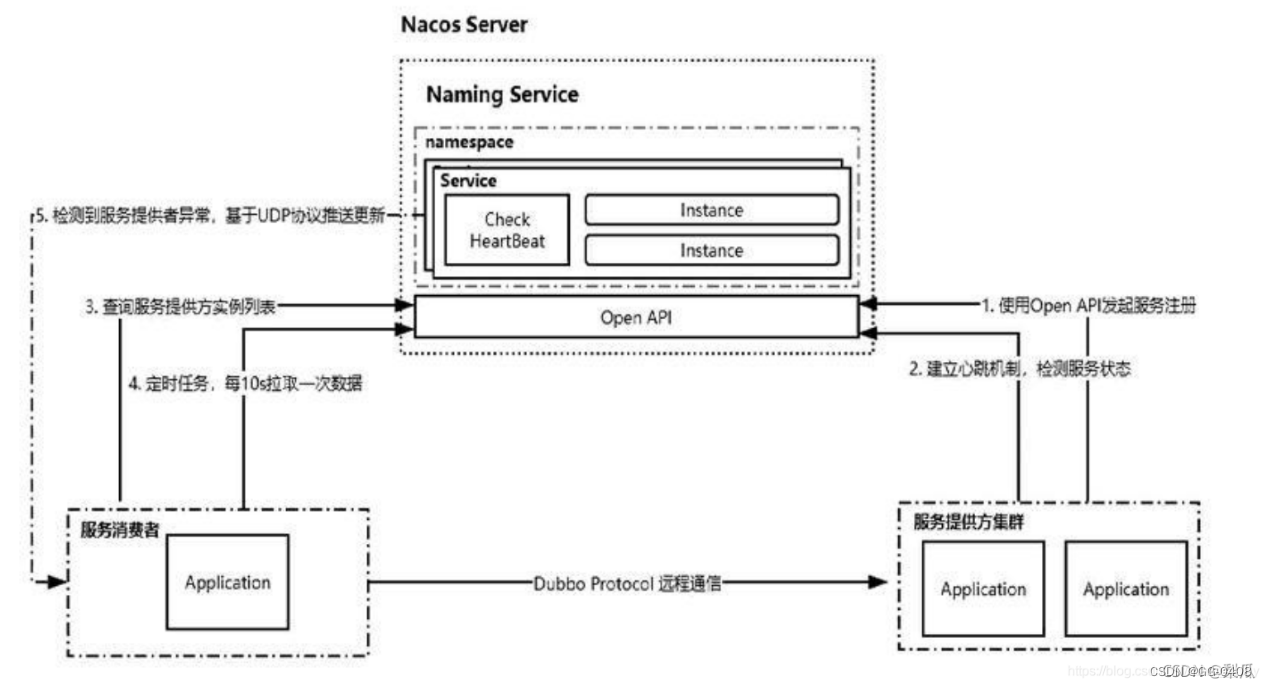
nacos和eureka的区别
nacos和eureka的区别 Eureka是什么 Eureka详解Nacos是什么 Nacos详解Nacos和Eureka的区别 CAP理论连接方式服务异常剔除操作实例方式自我保护机制 Eureka是什么 Eureka 是Spring Cloud 微服务框架默认的也是推荐的服务注册中心,由Netflix公司与2012将其开源出来,Eureka基于RE…...

canvas.toDataURL生成图片报错的解决方案
问题原因: toDataURL方法存在跨域限制,如果执行时dom内含有跨域的图片则浏览器执行时会报错。 这个根据不同的系统有不同的表现,例如:生成完毕但控制台有warning类型的警告,或者直接异常报error。 解决思路ÿ…...
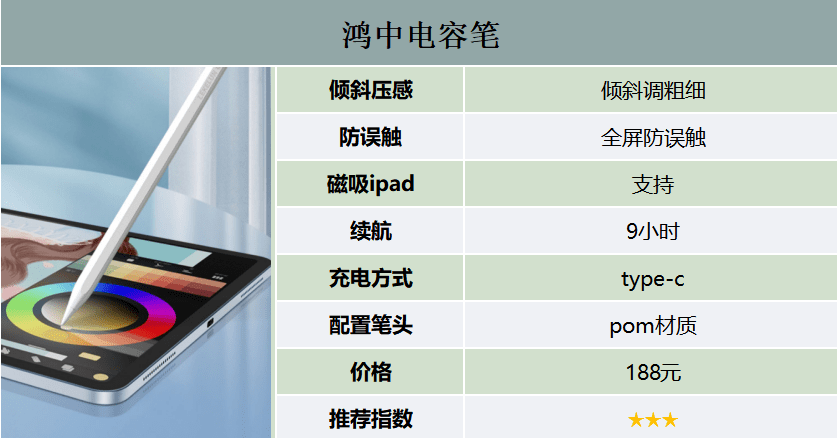
电容笔和Apple pencil的区别是什么?好用电容笔推荐
Apple Pencil与目前市场上常见的电容笔最大的不同之处在于,普通电容笔并不具备苹果Pencil特有的重力压感,而仅仅是一种倾斜的压感。不过,其在其它方面的表现也很出色,与Apple Pencil相似,而且价格仅为200元。现在&…...

关于onnx 转ncnn 的问题
文章目录修改模型Detect层设计转换后处理优质文章由于有些操作是没法支持的 如5维的操作: Unsupported slice axes ! Unsupported slice axes ! Unsupported slice axes ! Unsupported slice axes ! Unsupported slice axes ! Unsupported slice axes !参考&#…...

设计模式之《责任链模式》
------《责任链模式》责任链模式的概念为什么用责任链模式工作中用在哪里设计思路代码实现总结责任链模式的概念 责任链模式是一种行为型设计模式,它允许你将请求沿着处理链传递,直到有一个处理者能够处理该请求为止。 在责任链模式中,每个…...
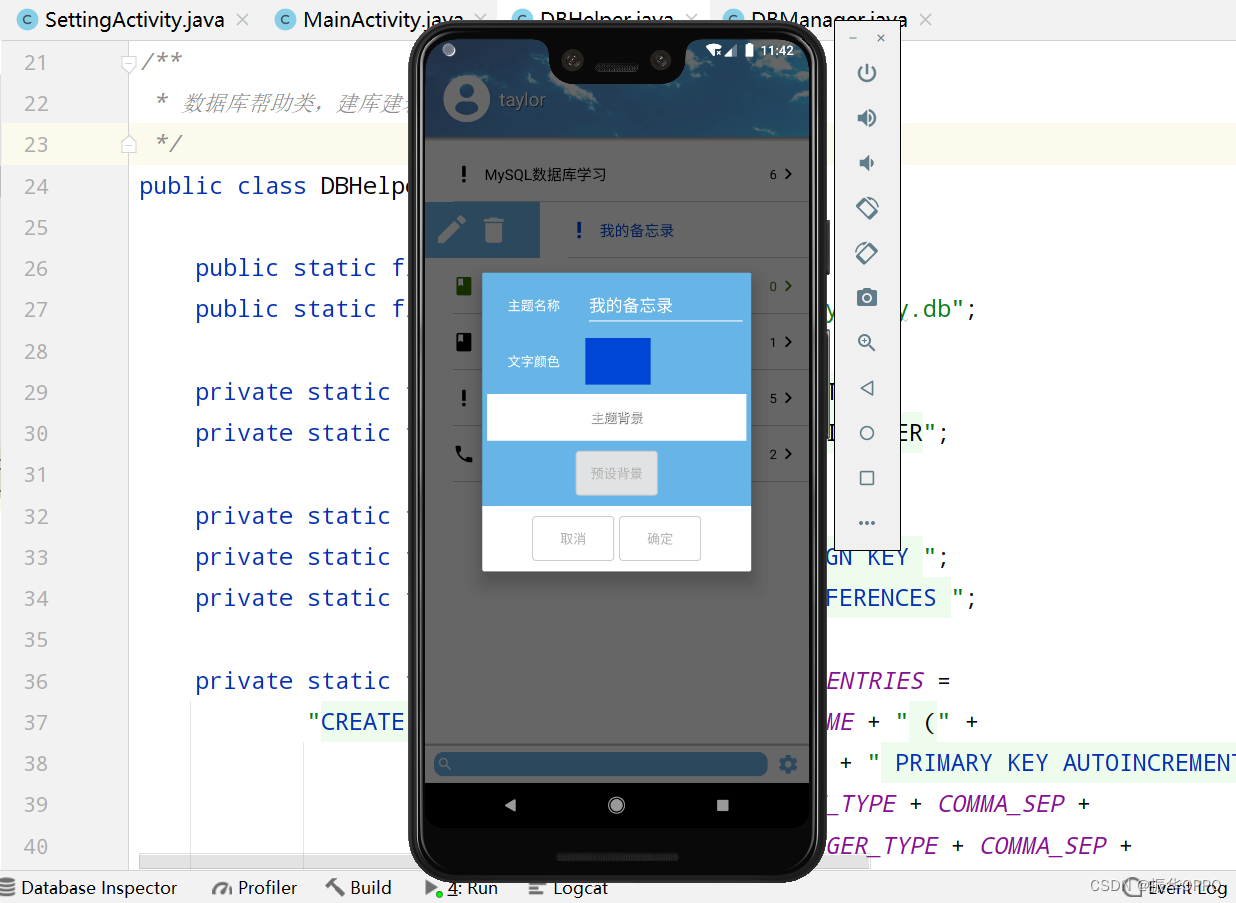
Android Studio实现多功能日记本
项目目录一、项目概述二、系统特点三、开发环境四、详细设计1、E-R图2、数据库3、系统设置五、运行演示一、项目概述 本次实现了功能实用且齐全的日记本,界面友好,使用便捷,采用MVC架构设计。使用SQLite数据库存储数据,数据表有主…...

只依赖Tensorrt和opencv的yolov5源代码
simple_yolo.hpp #ifndef SIMPLE_YOLO_HPP #define SIMPLE_YOLO_HPP/*简单的yolo接口,容易集成但是高性能 */#include <vector> #include <memory> #include <string> #include <future> #include <opencv2/opencv.hpp>namespace Si…...
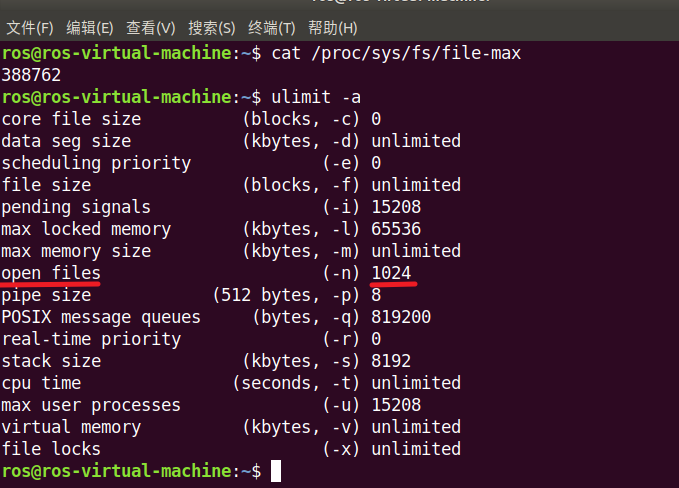
多路I/O转接 poll(了解)
poll() 的机制与 select() 类似,与 select() 在本质上没有多大差别,管理多个描述符也是进行轮询,根据描述符的状态进行处理,但是 poll() 没有最大文件描述符数量的限制(但是数量过大后性能也是会下降)。 p…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
