选择排序的简单理解
详细描述
选择排序的工作原理是:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾,以此类推,直到全部待排序的数据元素的个数为零。
选择排序详细的执行步骤如下:
- 初始状态:无序区为 R[1..n],有序区为空;
- 第 i 趟排序 (i=1,2,3…n-1) 开始时,当前有序区和无序区分别为 R[1...i-1] 和 R[i...n]。该趟排序从当前无序区中选出关键字最小的记录 R[k],将它与无序区的第 1 个记录 R 交换,使 R[1...i] 和 R[i+1...n] 分别变为记录个数增加 1 个的新有序区和记录个数减少 1 个的新无序区;
- 经过 n-1 趟,无序序列就有序化了。
算法图解
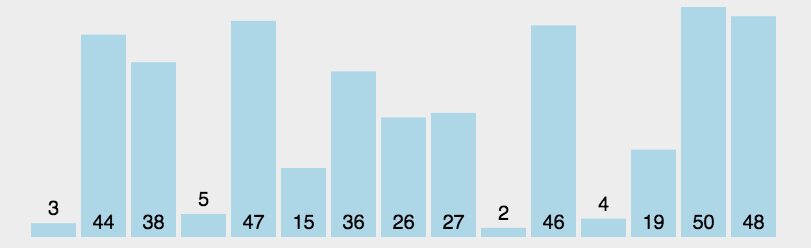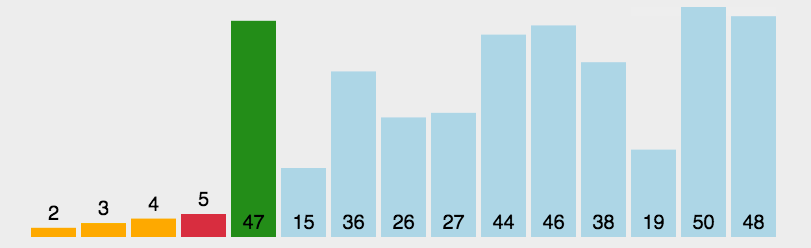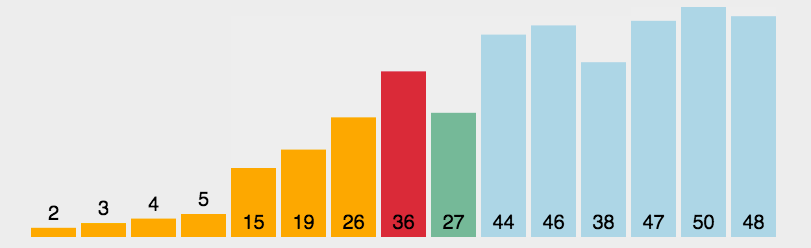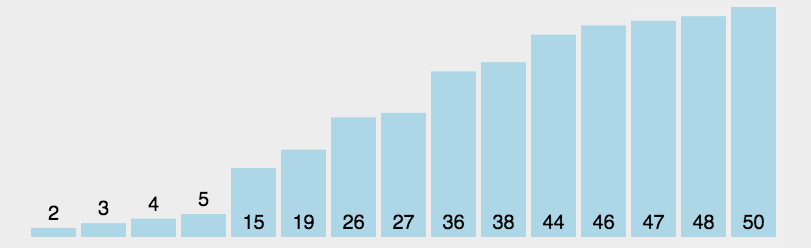
问题解疑
为什么选择排序是不稳定的?
虽然原理上存在有序区和无序区的区分,但是选择排序算法为了提高空间的使用率,使用的是原地交换方式。
与冒泡排序两两比较交换不同,选择排序算法是最小的元素与固定位置的元素进行交换,当这个固定位置的元素被交换到另一个位置之后,也就有可能导致相等的数字次序变化。
选择排序的时间复杂度是多少?
无论原序列是有序还是无序,选择排序都需要对序列做完整的遍历,即最好情况时间复杂度和最坏情况时间复杂度都是 O(n2);平均时间复杂度是 O(n2)。
代码实现
排序接口
package cn.fatedeity.algorithm.sort; | |
/** | |
* 排序接口 | |
*/ | |
public interface Sort { | |
int[] sort(int[] numbers); | |
} |
排序抽象类
package cn.fatedeity.algorithm.sort; | |
/** | |
* 排序抽象类 | |
*/ | |
public abstract class AbstractSort implements Sort { | |
protected void swap(int[] numbers, int src, int target) { | |
int temp = numbers[src]; | |
numbers[src] = numbers[target]; | |
numbers[target] = temp; | |
} | |
} |
选择排序类
package cn.fatedeity.algorithm.sort; | |
/** | |
* 选择排序类 | |
*/ | |
public class SelectionSort extends AbstractSort { | |
@Override | |
public int[] sort(int[] numbers) { | |
if (numbers.length <= 1) { | |
return numbers; | |
} | |
for (int i = 0; i < numbers.length - 1; i++) { | |
for (int j = i + 1; j < numbers.length; j++) { | |
// 选取到小的值做交换 | |
if (numbers[i] <= numbers[j]) { | |
continue; | |
} | |
this.swap(numbers, i, j); | |
} | |
} | |
return numbers; | |
} | |
} |
详细描述
选择排序的工作原理是:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾,以此类推,直到全部待排序的数据元素的个数为零。
选择排序详细的执行步骤如下:
- 初始状态:无序区为 R[1..n],有序区为空;
- 第 i 趟排序 (i=1,2,3…n-1) 开始时,当前有序区和无序区分别为 R[1...i-1] 和 R[i...n]。该趟排序从当前无序区中选出关键字最小的记录 R[k],将它与无序区的第 1 个记录 R 交换,使 R[1...i] 和 R[i+1...n] 分别变为记录个数增加 1 个的新有序区和记录个数减少 1 个的新无序区;
- 经过 n-1 趟,无序序列就有序化了。
算法图解

问题解疑
为什么选择排序是不稳定的?
虽然原理上存在有序区和无序区的区分,但是选择排序算法为了提高空间的使用率,使用的是原地交换方式。
与冒泡排序两两比较交换不同,选择排序算法是最小的元素与固定位置的元素进行交换,当这个固定位置的元素被交换到另一个位置之后,也就有可能导致相等的数字次序变化。
选择排序的时间复杂度是多少?
无论原序列是有序还是无序,选择排序都需要对序列做完整的遍历,即最好情况时间复杂度和最坏情况时间复杂度都是 O(n2);平均时间复杂度是 O(n2)。
代码实现
排序接口
package cn.fatedeity.algorithm.sort; | |
/** | |
* 排序接口 | |
*/ | |
public interface Sort { | |
int[] sort(int[] numbers); | |
} |
排序抽象类
package cn.fatedeity.algorithm.sort; | |
/** | |
* 排序抽象类 | |
*/ | |
public abstract class AbstractSort implements Sort { | |
protected void swap(int[] numbers, int src, int target) { | |
int temp = numbers[src]; | |
numbers[src] = numbers[target]; | |
numbers[target] = temp; | |
} | |
} |
选择排序类
package cn.fatedeity.algorithm.sort; | |
/** | |
* 选择排序类 | |
*/ | |
public class SelectionSort extends AbstractSort { | |
@Override | |
public int[] sort(int[] numbers) { | |
if (numbers.length <= 1) { | |
return numbers; | |
} | |
for (int i = 0; i < numbers.length - 1; i++) { | |
for (int j = i + 1; j < numbers.length; j++) { | |
// 选取到小的值做交换 | |
if (numbers[i] <= numbers[j]) { | |
continue; | |
} | |
this.swap(numbers, i, j); | |
} | |
} | |
return numbers; | |
} | |
} |
相关文章:

选择排序的简单理解
详细描述 选择排序的工作原理是:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾…...

使用js封装一个循环链表
直接不说废话,直接上代码,这里继承了单向链表的类LinkList ,可以查看之前的文章,点这里 class Node {constructor(element) {this.element element;this.next null;} }class CirularLinkedList extends LinkList {constructor(…...
NumPy 秘籍中文第二版:二、高级索引和数组概念
原文:NumPy Cookbook - Second Edition 协议:CC BY-NC-SA 4.0 译者:飞龙 在本章中,我们将介绍以下秘籍: 安装 SciPy安装 PIL调整图像大小比较视图和副本翻转 Lena花式索引位置列表索引布尔值索引数独的步幅技巧广播数…...

新品-图灵超频工作站GT430M介绍
曾经历史 UltraLAB GTxxxM系列是西安坤隆公司专注于超频高速计算应用的图形工作站。 2008年 获取排名第一、二的中国象棋软件均采用该机型。 2019年 推出采用Intel 超频Xeon(28核4.8GHz)显著提升电磁仿真频域算法求解、第一个解决8K视频解码与渲染。 今…...

js时间格式化精确到毫秒
/*** 数字前置补零* param value 值* param length 位数* returns {string}*/ export function digit(value, length 2) {if (typeof value "undefined" ||value null ||String(value).length > length) {return value;}return (Array(length).join("0&qu…...

QT样式表详解
本文详细介绍qt的样式表,包含样式表如何使用,常见语句和选择器。 背景说明 样式表用于设置外观,他是设置控件外观的方式之一。其他方式如下: 控件的成员函数,如QWidget::setBackground样式表调色板 优先级依次提高…...

最值得入手的好物有哪些,推荐几款实用的数码好物
随着科技的进步,越来越多的数码产品不断的出现在我们的生活中,这其中也不乏一些实用的数码产品,让我们可以享受更舒适的生活,提高我们的工作效率。下面就给大家分享几款我最近使用过的一些数码产品,它们不仅功能强大而…...
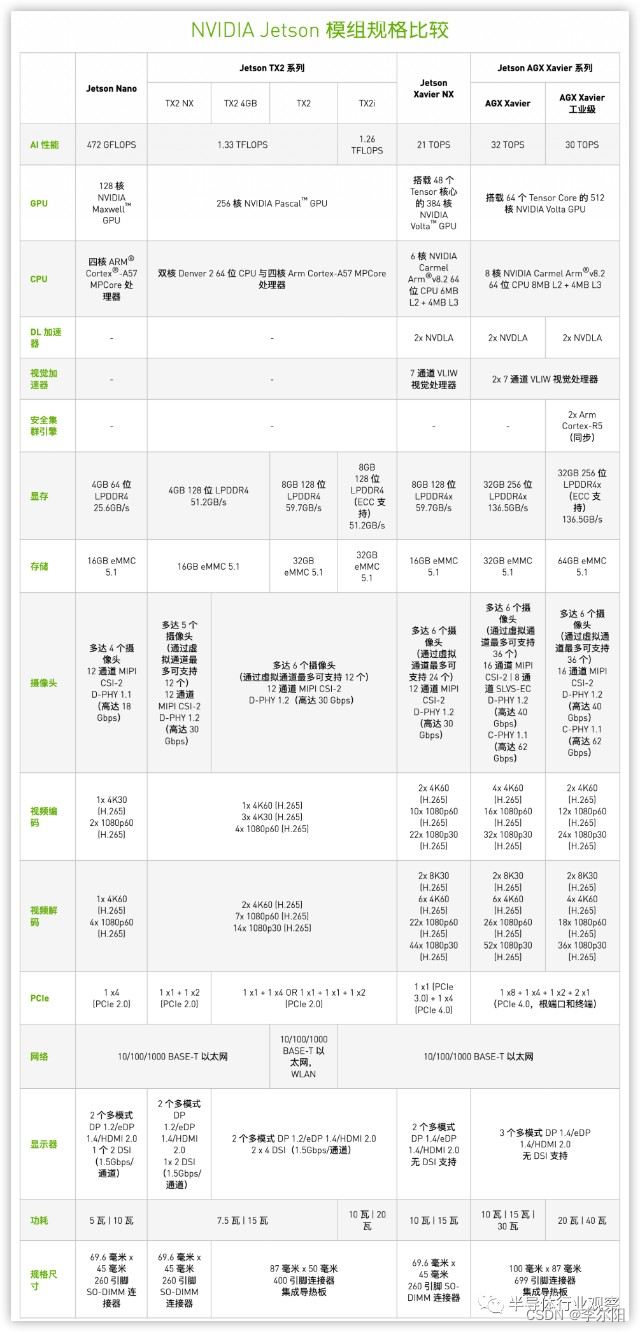
【20230407】NVIDIA显卡算力、Jetson比较
1 基本概念 1.1 算力单位 TOPS:指的是每秒钟可以执行的整数运算次数,它代表着计算机在处理图像、音频等任务时的处理能力。TOPS的单位是万亿次每秒(trillion operations per second)。一般是指整数运算能力INT8。 TFLOPS&#…...

dsl语法
查询 1.查询所有(默认有分页查询) #查询所有 GET /hotel/_search {"query": {"match_all": {}} } 2.match查询(条件查询)-----包含四川和外滩的信息,信息匹配度越高越靠前,两者存在一…...
不让CPU偷懒
文章资料摘自——《程序员的自我修养》 为了防止cpu执行完该程序后需要等待程序员手动加入下一个程序,才可以继续运行,这里大大浪费了cpu的效率,要知道cpu是十分昂贵的。 多道程序 在计算机发展的早期,CPU使用十分不方便&#x…...
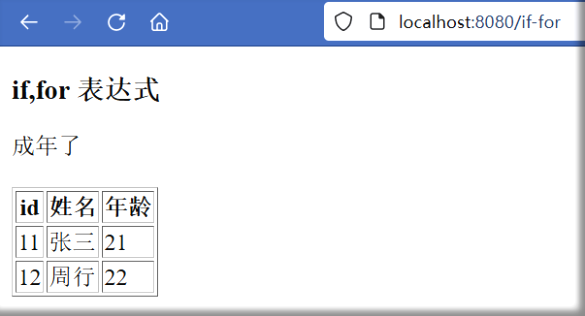
动力节点王鹤SpringBoot3笔记——第七章 视图技术Thymeleaf
目录 第七章 视图技术Thymeleaf 前言 7.1 表达式 7.2 if-for 第七章 视图技术Thymeleaf 前言 Thymeleaf 是一个表现层的模板引擎, 一般被使用在 Web 环境中,它可以处理 HTML, XML、 JS 等文档,简单来说,它可以将 JSP 作…...

从比特保存和信息保存看数字资源长期保存
引用IBM以色列海法实验室的观点,数字资源长期保存包含两个层面含义,即比特保存与信息保存。也就是说,要实现数字资源的长期保存,必须同时做到比特保存和信息保存。 一 概念 01 比特保存,也叫物理保存,主…...

兰伯特光照模型(Lambert Lighting)和半兰伯特光照模型(Half-Lanbert)
关于漫反射 光打到凹凸不平的平面上,光线会被反射到四面八方,被称为漫反射 关于这种模型,由于光线由于分散,所以进入人眼的光线强度和观察角度没有区别 在A点和B点接收到的光线强度是一样的 在漫反射下,光线强度只和光…...
Python 进阶指南(编程轻松进阶):二、环境配置和命令行
原文:http://inventwithpython.com/beyond/chapter2.html 环境配置是配置你的计算机环境,以便你写代码的过程。这包括安装任何必要的工具,配置它们,以及处理安装过程中的任何问题。没有一键配置这种傻瓜式操作过程,因为…...

求职半年,三月成功拿到阿里offer,分享一波面经...
前言 不论是校招还是社招都避免不了各种⾯试、笔试,如何去准备这些东⻄就显得格外重要。不论是笔试还是⾯试都是有章可循的,我这个“有章可循”说的意思只是说应对技术⾯试是可以提前准备,所谓不打无准备的仗就是这个道理。 以下为大家&…...

餐饮店的运营需要考虑哪些方面
餐饮店的运营需要多方面的考虑和规划,以下是传递宝APP上一些常用的餐饮店运营方法: 1.定位:明确餐饮店的定位和目标客户群体,针对不同的客户需求,提供个性化的服务和产品,比如是附近的上班族,还…...

Multi-modal Alignment using Representation Codebook
Multi-modal Alignment using Representation Codebook 题目Multi-modal Alignment using Representation Codebook译题使用表示代码集的多模态对齐期刊/会议CVPR 摘要:对齐来自不同模态的信号是视觉语言表征学习(representation learning)的…...

关于vector的emplace_back和push_back的区别
实验代码: class A { public:A(int x) {x x;cout << "construct A" << endl;}A(const A& a) {x a.x;cout << "copy construct A" << endl;}A(const A&& a) {cout << "Move construct A"…...

Vue——表单输入绑定
目录 基本用法 文本 多行文本 复选框 选择器 值绑定 复选框 单选按钮 选择器选项 修饰符 .lazy .number .trim 组件上的 v-model 在前端处理表单时,我们常常需要将表单输入框的内容同步给 JavaScript 中相应的变量。手动连接值绑定…...
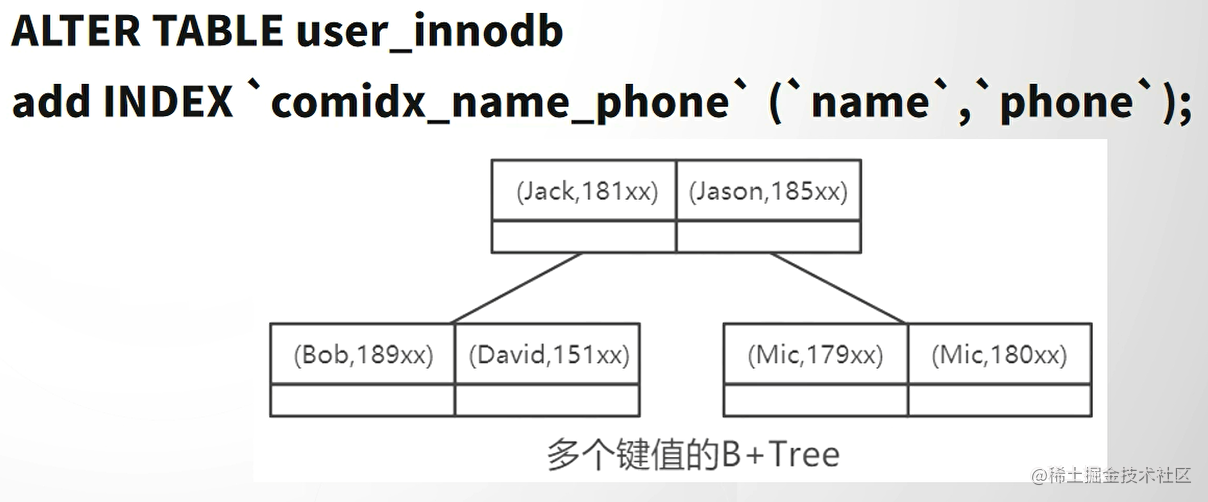
MySQL性能优化(二)索引
文章目录优化手段准备案例索引的本质索引的数据结构不同存储引擎中索引的实践MyIsam (索引没有主次之分、都存放在MYI文件)主键索引其他索引InnoDB(数据即索引、索引即数据)主键索引——聚集索引聚集索引其他索引没有主键的情况&a…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
