LC-1042. 不邻接植花(四色问题(染色法))
1042. 不邻接植花
难度中等198
有 n 个花园,按从 1 到 n 标记。另有数组 paths ,其中 paths[i] = [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中,你打算种下四种花之一。
另外,所有花园 最多 有 3 条路径可以进入或离开.
你需要为每个花园选择一种花,使得通过路径相连的任何两个花园中的花的种类互不相同。
以数组形式返回 任一 可行的方案作为答案 answer,其中 answer[i] 为在第 (i+1) 个花园中种植的花的种类。花的种类用 1、2、3、4 表示。保证存在答案。
示例 1:
输入:n = 3, paths = [[1,2],[2,3],[3,1]]
输出:[1,2,3]
解释:
花园 1 和 2 花的种类不同。
花园 2 和 3 花的种类不同。
花园 3 和 1 花的种类不同。
因此,[1,2,3] 是一个满足题意的答案。其他满足题意的答案有 [1,2,4]、[1,4,2] 和 [3,2,1]
示例 2:
输入:n = 4, paths = [[1,2],[3,4]]
输出:[1,2,1,2]
示例 3:
输入:n = 4, paths = [[1,2],[2,3],[3,4],[4,1],[1,3],[2,4]]
输出:[1,2,3,4]
提示:
1 <= n <= 1040 <= paths.length <= 2 * 104paths[i].length == 21 <= xi, yi <= nxi != yi- 每个花园 最多 有 3 条路径可以进入或离开
哈希表实现(染色法)
题解:https://leetcode.cn/problems/flower-planting-with-no-adjacent/solution/liang-chong-xie-fa-ha-xi-biao-shu-zu-wei-7hm8/
四色定理(世界近代三大数学难题之一),又称四色猜想、四色问题,是世界三大数学猜想之一。
四色问题的内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”也就是说在不引起混淆的情况下一张地图只需四种颜色来标记就行。
用数学语言表示即“将平面任意地细分为不相重叠的区域,每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。”这里所指的相邻区域是指有一整段边界是公共的。如果两个区域只相遇于一点或有限多点就不叫相邻的。
- 问题相当于用 4 种颜色给图中的每个节点染色,要求相邻节点颜色不同。而「所有花园最多有 3 条路径可以进入或离开」,这相当于图中每个点的度数至多为 3,那么只要选一个和邻居不同的颜色即可。
class Solution {public int[] gardenNoAdj(int n, int[][] paths) {List<Integer> g[] = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for(int[] e : paths){int x = e[0]-1, y = e[1]-1; // 编号改为从0开始g[x].add(y);g[y].add(x);}int[] color = new int[n];for(int i = 0; i < n; i++){// 至多有4种颜色,每个节点至多3个路径// 因此只要选与邻居不同的颜色即可boolean[] used = new boolean[5];for(int j : g[i]){used[color[j]] = true;}while(used[++color[i]]); // 找到一个邻居没有用过的颜色// for color[i]++; used[color[i]]; color[i]++ {}}return color;}
}
位运算实现
class Solution {public int[] gardenNoAdj(int n, int[][] paths) {List<Integer> g[] = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for(int[] e : paths){int x = e[0]-1, y = e[1]-1; // 编号改为从0开始g[x].add(y);g[y].add(x);}int[] color = new int[n];for(int i = 0; i < n; i++){int mask = 1; // 由于颜色是 1~4,把 0 加入 mask 保证下面不会算出 0for(int j : g[i]){mask |= 1 << color[j];}color[i] = Integer.numberOfTrailingZeros(~mask);// 一个数与它的相反数与运算-1可以得到末尾0的个数}return color;}
}
相关文章:
))
LC-1042. 不邻接植花(四色问题(染色法))
1042. 不邻接植花 难度中等198 有 n 个花园,按从 1 到 n 标记。另有数组 paths ,其中 paths[i] [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中,你打算种下四种花之一。 另外,所有花园 最多 有 3 条路径可以进入…...
)
python实战应用讲解-【numpy科学计算】scikits-learn模块(附python示例代码)
目录 Numpy 安装scikits-learn 准备工作 具体步骤 Numpy 加载范例数据集 具体步骤...

大数据开发必备面试题Spark篇01
1、Hadoop 和 Spark 的相同点和不同点? Hadoop 底层使用 MapReduce 计算架构,只有 map 和 reduce 两种操作,表达能力比较欠缺,而且在 MR 过程中会重复的读写 hdfs,造成大量的磁盘 io 读写操作,所以适合高时…...
SpringBoot整合xxl-job详细教程
SrpingBoot整合xxl-job,实现任务调度说明调度中心执行器调试整合SpringBoot说明 Xxl-Job是一个轻量级分布式任务调度平台,其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品线,开箱即用。Xxl-Job有…...
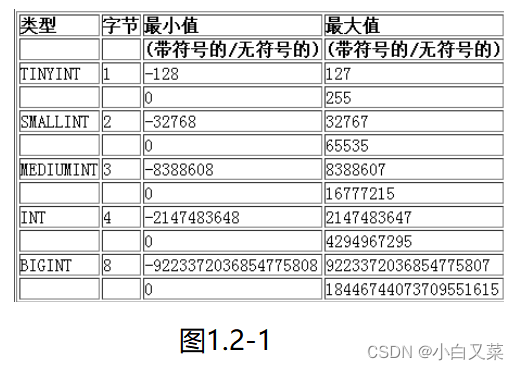
【MySQL--04】数据类型
文章目录1.数据类型1.1数据类型分类1.2数值类型1.2.1tinyint类型1.2.2bit类型1.2.3小数类型1.2.3.1 float1.2.3.2 decimal1.3字符串类型1.3.1 char1.3.2 varchar1.3.3char和varchar的比较1.4日期和时间类型1.5 enum和set1.5.1 enum1.5.2 set1.5.3 示例1.数据类型 1.1数据类型分…...

git 将其它分支的文件检出到工作区
主要是使用如下命令: git checkout [-f|--ours|--theirs|-m|--conflict<style>] [<tree-ish>] [--] <pathspec>…覆盖与 pathspec 匹配的文件的内容。当没有给出<tree-ish> (通常是一个commit)时,用 index 中的内容覆盖工作树…...

人工智能的最大危险是什么?
作者:GPT(AI智学习) 链接:https://www.zhihu.com/question/592107303/answer/2966857095 来源:知乎 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 首先:人工智能为人类带来了很多益处&…...
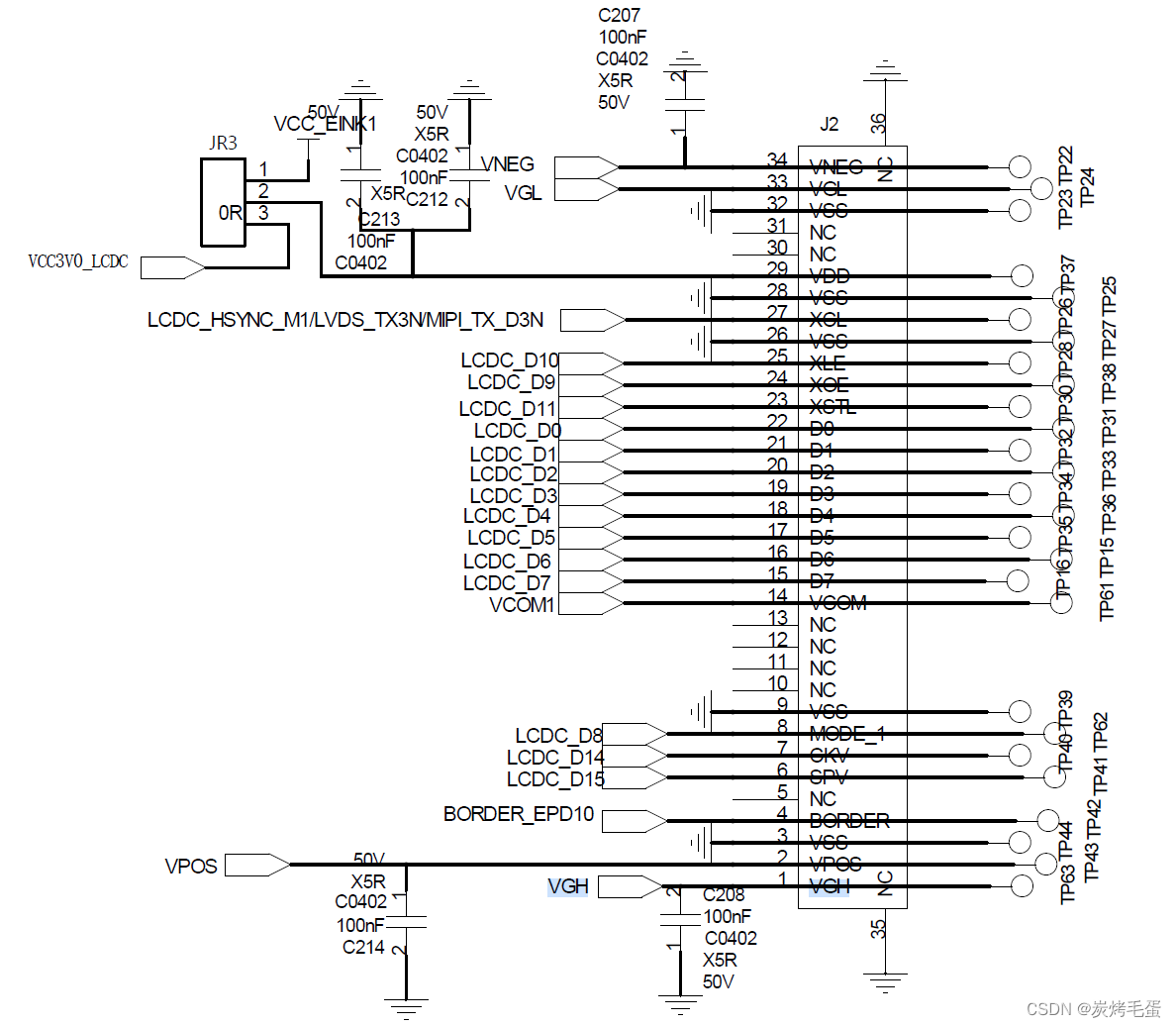
rk3568点亮E-ink
rk3568 Android11/12 适配 E-ink “EINK”是英语ElectronicInk的缩写。翻译成中文为“电子墨水”。电子墨水由数百万个微胶囊(Microcapsules)所构成,微胶囊的大小约等同于人类头发的直径。每个微胶囊里含有电泳粒子──带负电荷的白色以及带正电荷的黑色粒子&#…...
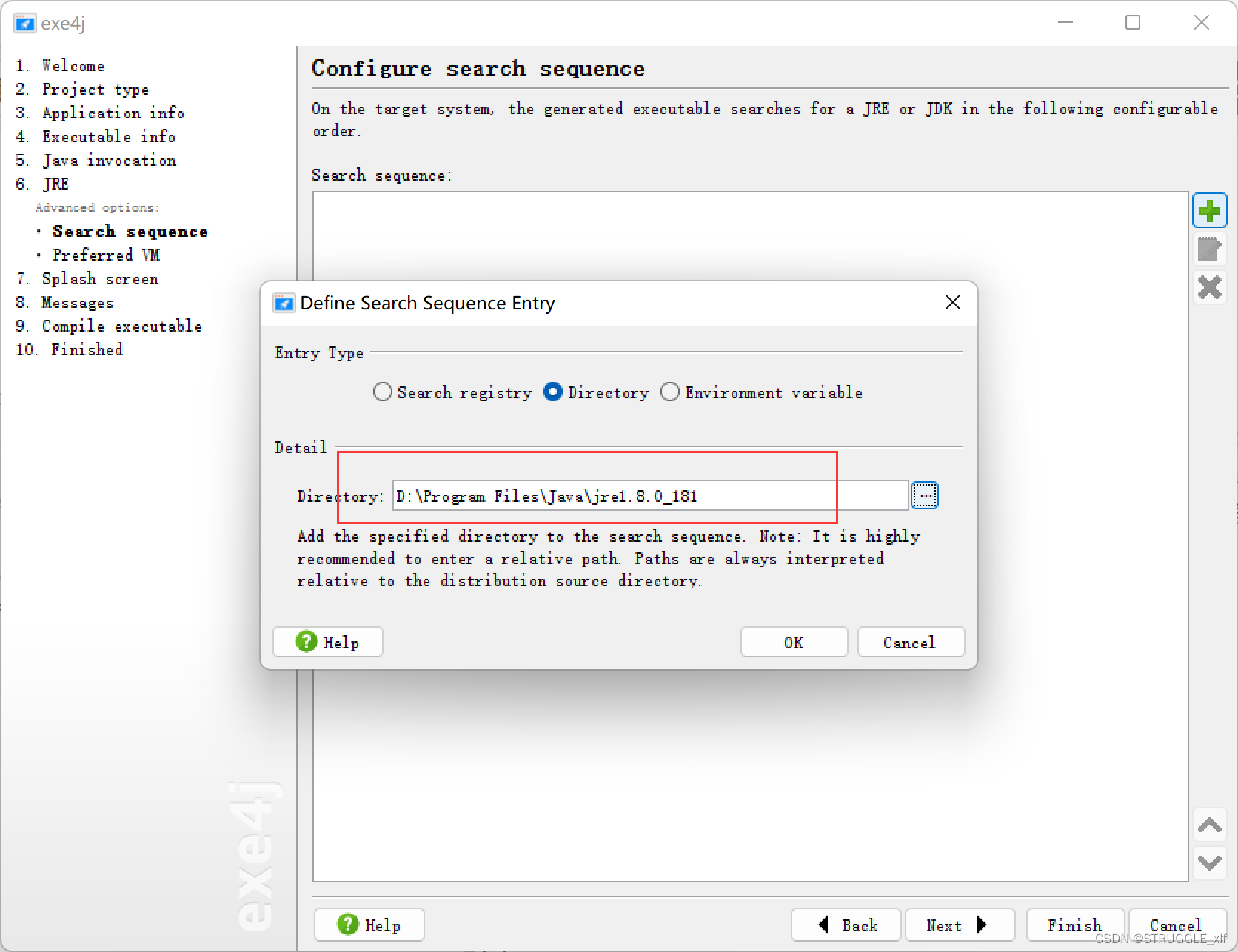
如何将Springboot项目通过IDEA打包成jar包,并且转换成可执行文件
首先在IDEA打开你的项目,需要确认项目可以正常运行,然后点击页面右侧的Maven,运行Lifecycle下的package, 此时在项目的target目录下就可以看到一个jar包 这个时候你可以在jar包所在目录下执行cmd窗口,运行 java -jar campus-market-0.0.1-S…...

总结:网卡
一、背景 经常听到eth0,bond0这些概念,好奇他们的区别,于是有了此篇文章记录下。 二、介绍 网卡:即网络接口板,又称网络适配器或NIC (网络接口控制器),是一块被设计用来允许计算机在计算机网络上进行通讯…...

Java这么卷,还有前景吗?
“Java很卷”、“大家不要再卷Java了”,经常听到同学这样抱怨。但同时,Java的高薪也在吸引越来越多的同学。不少同学开始疑惑:既然Java这么卷,还值得我入行吗? 首先先给你吃一颗定心丸:现在选择Java依然有…...
--gocron)
后端简易定时任务框架选择(Python/Go)--gocron
文章目录前言实现后语前言 在使用Python的web框架中,包括flask/Django,其中大量用到celery;celery作为异步任务使用的多,同时也会用celery来跑些定时任务,比如每晚定时跑脚本、跑数据统计等闲时任务。但随着任务量的增…...

【GStreamer学习】之GStreamer基础教程
目标 没有什么比在屏幕上打印出“Hello World”更能获得对软件库的第一印象了! 但是由于我们正在学习多媒体框架,所以我们将输出“Hello World!”改为播放视频。 不要被下面的代码量吓到:只有 4 行是真正需要的, 其…...

各类Round-Robin总结,含Verilog实现
1. Fixed Priority Arbitrary 固定优先级就是指每个req的优先级是不变的,即优先级高的先被处理,优先级低的必须是在没有更高优先级的req的时候才会被处理。所以转化为数学模型就是找出req序列中第一个为1的位置,然后将其转换为onehot。 例如: req[3:0] = 4b1100 ==> g…...

《软件设计师-知识点》
1、指令流水线 (一)一条指令的执行过程可分为三个阶段:取指、分析、执行。 取指:根据PC(程序计数器)内容访问主存储器,取出一条指令送到IR(指令寄存器)中。 分析&…...

mysql 同义词_数据库中的同义词synonym
一、Oracle数据只有一个实例(简单理解就是Oracle 只能建立一个数据库,不像MySQL,它下面可以创建N个库),那么Oracle是根据用户灵活去管理的;这点读起来、理解 起来也不那么难,但是除非自己亲自实现一把才理解深入点&…...
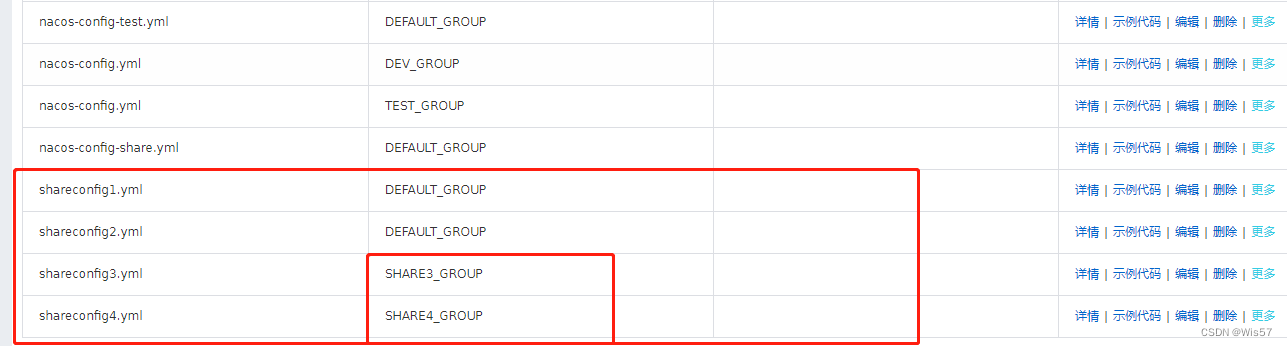
Nacos共享配置
本文介绍一下Nacos作为配置中心时,如何读取共享配置 我的环境 Windows10JDK8SpringCloud:Finchley.RELEASESpringBoot:2.0.4.RELEASEspring-cloud-alibaba-dependencies:0.2.2.RELEASENacos-server:1.0.1 本文的项目…...
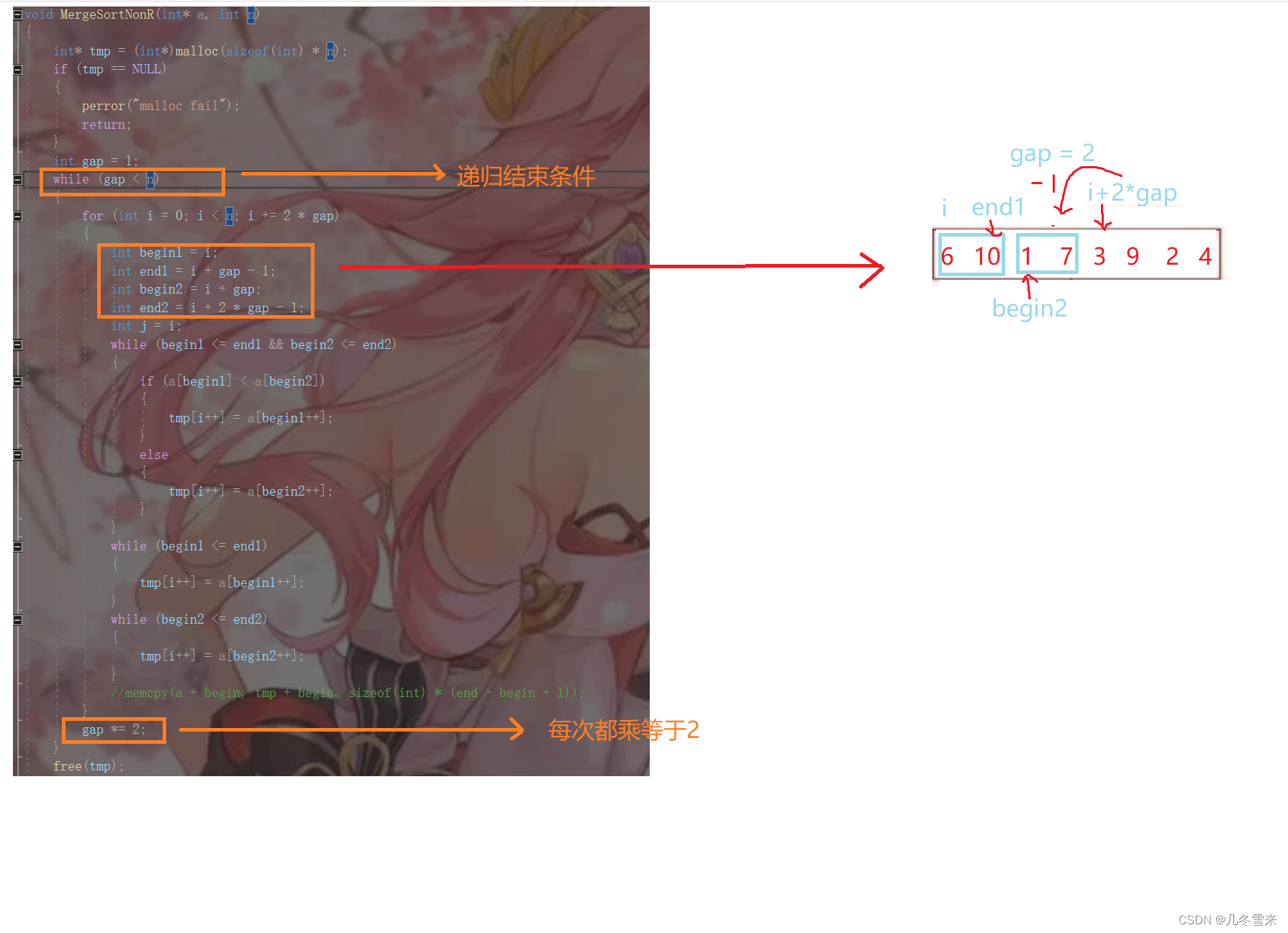
数据结构——排序(4)
作者:几冬雪来 时间:2023年4月12日 内容:数据结构排序内容讲解 目录 前言: 1.快速排序中的递归: 2.小区间优化: 3.递归改非递归: 4.归并排序: 5.归并排序的非递归形式&…...

C++13:搜索二叉树
目录 搜索二叉树概念 模拟实现搜索二叉树 插入函数实现 插入函数实现(递归) 查找函数实现 删除函数实现 删除函数实现(递归) 中序遍历实现 拷贝构造函数实现 析构函数实现 赋值重载 我们在最开始学习二叉树的时候,…...
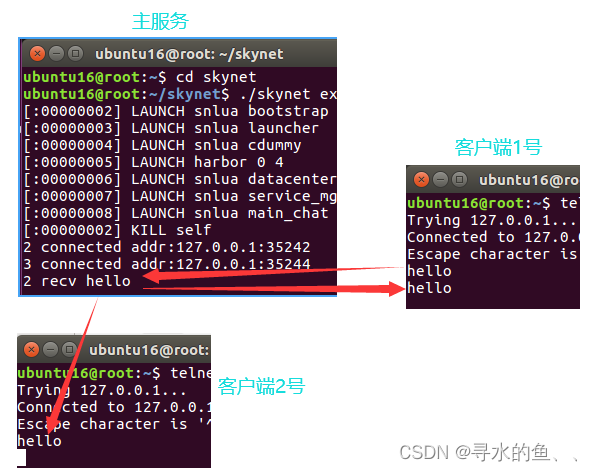
【从零开始学Skynet】基础篇(五):简易聊天室
在游戏中各玩家之间都可以进行聊天之类的交互,在这一篇中,我们就来实现一个简易的聊天室功能,这在上一篇代码的基础上很容易就能实现。1、功能需求 客户端发送一条消息,经由服务端转发,所有在线客户端都能收到…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
