C++13:搜索二叉树
目录
搜索二叉树概念
模拟实现搜索二叉树
插入函数实现
插入函数实现(递归)
查找函数实现
删除函数实现
删除函数实现(递归)
中序遍历实现
拷贝构造函数实现
析构函数实现
赋值重载
我们在最开始学习二叉树的时候,最开始接触的就是堆,但那个结构上并不是真正的二叉树,后来又借助链表实现了真正的结构上的二叉树,二叉树不仅仅只是在OJ题上刁难我们,其实当实现了一定的节点逻辑之后,也可以形成效率极高的数据结构,这个二叉树就是搜索二叉树。
搜索二叉树概念
对于一颗搜索二叉树来说,它的节点内存储的值遵循如下的规则
- 右子树节点的值一定大于当前节点的值
- 左子树节点的值一定小于当前节点的值
而对于其结构来说
- 搜索二叉树不允许已存在于二叉树内部的值再次插入
- 搜索二叉树的左右子树也必须是搜索二叉树
- 数据插入的顺序不同,搜索二叉树的形状也会不同
这样的结构让搜索二叉树的效率在平衡的情况下效率变得非常的高
- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log_2 N
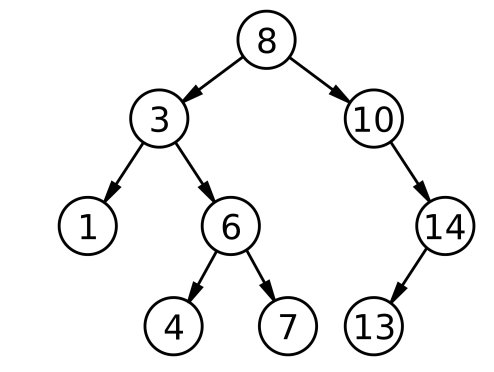
但是当插入数据是有序的时候,搜索二叉树会退化成单叉树
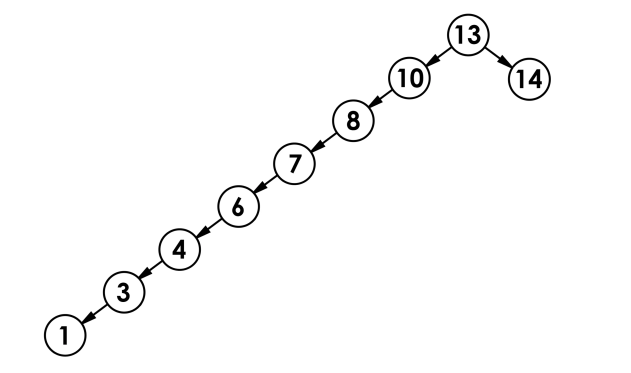
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N
其整体的树结构以及逻辑就差不多如上所述了,接下来就是模拟实现。
模拟实现搜索二叉树
插入函数实现
首先先定义一下节点的结构,我们加入模板。
template<class K>struct BSNode{BSNode<K>* _left;BSNode<K>* _right;K _key;BSNode(K val = K()):_left(nullptr), _right(nullptr), _key(val){}};接着我们实现插入函数,逻辑并不困难,总结如下:
- 树为空,则直接新增节点,赋值给root指针
- 树不空,按二叉搜索树性质查找插入位置,插入新节点
- 插入有成功与失败一说,假如插入的值已存在于树内,则插入失败
- 以K值为判定条件插入左子树或者右子树,比K大插右子树,比K小插左子树
- 需要额外创建一个父节点来链接节点。
//以K值为判定条件插入左子树或者右子树,比K大插右子树,比K小插左子树//若遇到相等的,插入失败,不插bool Insert(const K& val){if (_root == nullptr){_root = new Node(val);return true;}Node* cur = _root;Node* parent = cur;while (cur){//比K小,往左子树走if (val < cur->_key){parent = cur;cur = cur->_left;}//比K大,往右子树走else if (val > cur->_key){parent = cur;cur = cur->_right;}//相等,插入不了,返回一个falseelse{return false;}}//跳出while时,也就是遇到空了,新建一个节点赋值然后链接节点if (parent->_key < val)parent->_right = new Node(val);else if (parent->_key > val)parent->_left = new Node(val);return true;}插入函数实现(递归)
二叉树的插入也可以是递归,毕竟二叉树的结构本身就适合递归
递归的逻辑:
- 终止条件:遇到了空,那么就是到位了,或者说一个空节点,创建节点准备链接
- 本次递归应该做的事:检查当前插入的值是否大于K,大于走右树,小于走左树
- 返回的信息:同循环版本,返回true Or false
但是这里有个问题,想要在类内部实现递归轻而易举,直接传递根节点即可,但是它的访问限定符是私有,这意味着我们无法在类外部调用这个递归插入,所以我们还需要额外实现一个GetRoot或者是私有的内嵌递归函数来获取到根。
其中,传递的形参必须是引用,因为递归的栈帧问题,要 是想要在递归的途中链接节点之间的指针,还需要额外的parent的节点,但会让程序变得冗杂,一个引用则可以非常巧妙地解决问题,因为正好上一层传递下来的引用就是父节点的别名,直接链接即可。
同样的,借助二级指针也是可以实现的,但是完全比不上引用。
bool InsertR(const K& val){return _InsertR(_root, val);}private:bool _InsertR(Node*& root,const K& val){//假如走到了空,那么就是到位了,或者是一个空树,创建节点准备链接if (root == nullptr){root = new Node(val);return true;}//大于,向右走if (val > root->_key)return _InsertR(root->_right, val);else if (val < root->_key)return _InsertR(root->_left, val);elsereturn false;}查找函数实现
查找的逻辑同插入没什么区别,也可以实现递归版本,在这里就不列出逻辑了。
//查找函数,找到了返回true,找不到返回falsebool Find(const K& val){Node* cur = _root;while (cur){//大于就向右边找if (val > cur->_key)cur = cur->_right;//小于就向左边查找else if (val < cur->_key)cur = cur->_left;//相等就找着了elsereturn true;}//没找着return false; }删除函数实现
删除的情况较多且有些复杂,逻辑如下:
删除有三种情况
- 删一个有孩子的节点,若其左为空,把右边给父节点,
- 若右边为空,则把左边的孩子给父节点
- 删一个带有多个孩子的节点,比较复杂,需要替换删除,期间也需要注意删除根的情况,找右子树的最小节点,也就是右子树的最左边的节点与被删除的节点交换,然后删去右子树最左节点。
情况1,2 示意图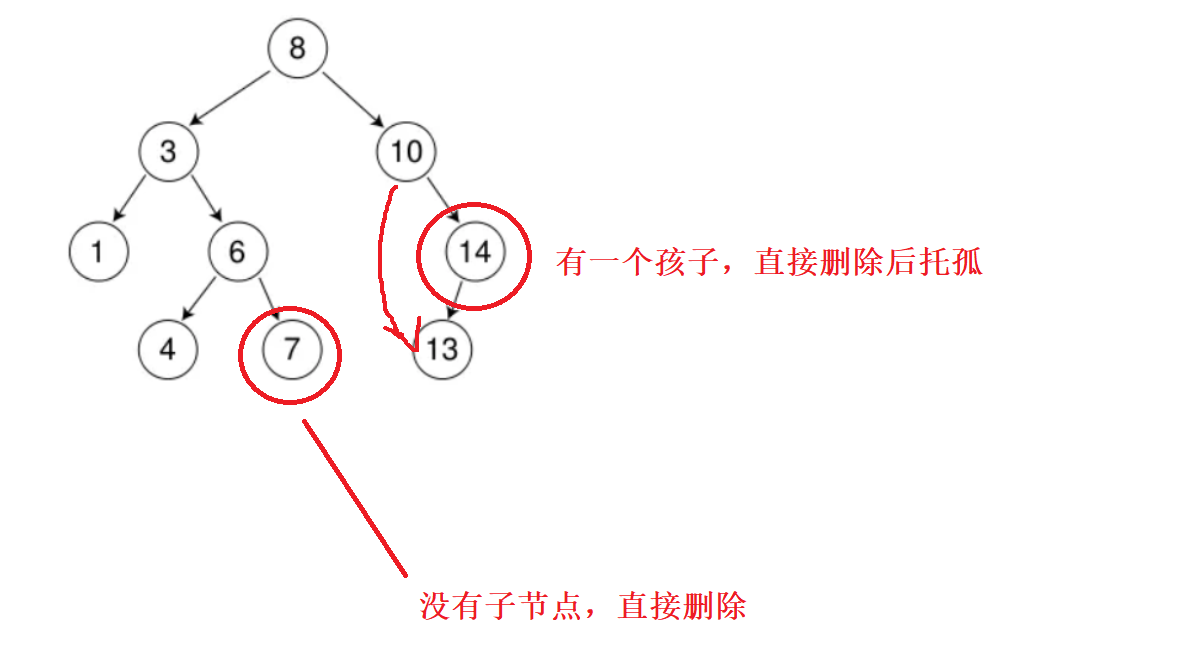
情况3示意图,图中示意为替换法逻辑,还需要额外处理删除根节点的情况。
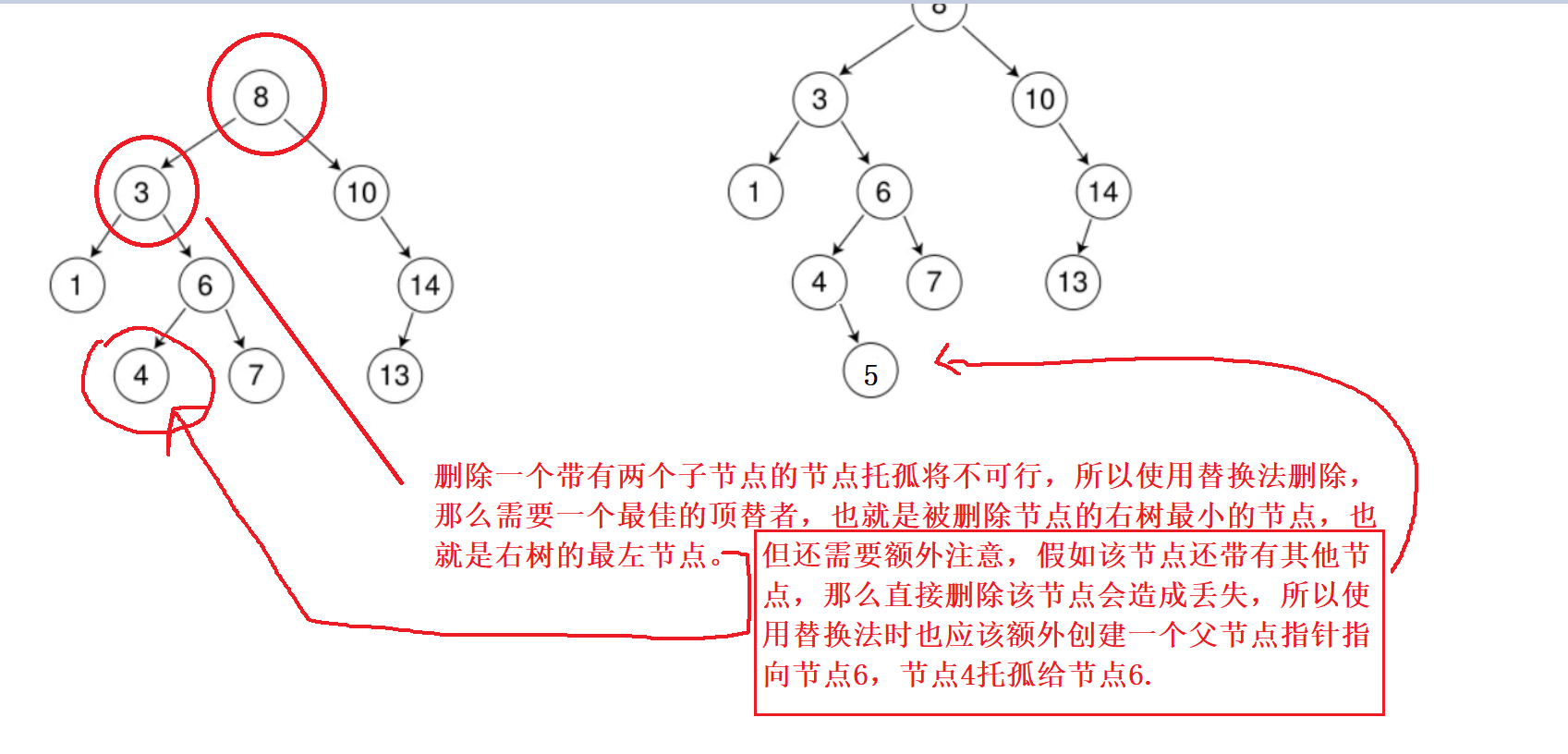
那么代码实现如下
bool erase(const K& val){Node* cur = _root;Node* parent = nullptr;while (cur){if (val > cur->_key){parent = cur;cur = cur->_right;}else if (val < cur->_key){parent = cur;cur = cur->_left;}//相等就找到了,找到后进行删除else{//左孩子为空,右孩子为空,以及左右都不为空,其中这三种情况下,还需要特殊处理删除根节点的时候//其中只有一个孩子的情况下,只需要托孤即可if (cur->_left == nullptr){//如果左孩子为空,那么先判断一下是不是根节点。if (cur == _root){//是根节点,直接让cur-的右边做根_root = cur->_right;}//删的不是根,直接托孤给parentelse{//需要被托孤的是到if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;cur = nullptr;}//有左孩子,没右孩子else if (cur->_right == nullptr){//如果是根,就把根给到左孩子if (cur == _root)_root = cur->_left;else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;cur = nullptr;}//左右孩子都不是空,需要替换删除,期间也需要注意删除根的情况else{//找右子树的最小节点,也就是右子树的最左边//先找最小值,有根判根//留一个parent,以防止min后面还有节点Node* minparent = cur;Node* min = cur->_right;while (min->_left){minparent = min;min = min->_left;}cur->_key = min->_key;//给完跟在删除min之前还要把min后面的节点都街上if (minparent->_left == min)minparent->_left = min->_right;elseminparent->_right = min->_right;delete min;min = nullptr;}return true;}}//没找着return false;}删除函数实现(递归)
主体逻辑同循环版本差不太多,需要注意的是替换法删除的部分,可以很巧妙的再次调用一次递归去删除被替换的节点。
bool _earseR(Node*& root, const K& val){if (root == nullptr)return false;if (root->_key > val){return _earseR(root->_left, val);}else if(root->_key < val){return _earseR(root->_right, val);}else//找到了{//叶子节点无需特殊处理,在处理单子树的过程中顺带解决了//没有左孩子,那么一定有右孩子,直接链接右孩子到父节点,这种情况是根节点的完全没有左子树,也就是直接更新根//用一个节点保存前根,Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else//交换,但是走的是递归,可以很巧妙的交换两个节点的值,然后再走递归去删掉替死鬼。{Node* min = root->_right;while (min->_left)min = min->_left;swap(root->_key, min->_key);return _earseR(root->_right, val);}delete del;del = nullptr;return true;}}Node* _root = nullptr;};中序遍历实现
这块就没啥好说的,除了记得需要额外内嵌一个递归函数。
void InOrder(){Node* root = GetRoot();_inorder(root);}void _inorder(Node* _root){if (_root == nullptr){return;}_inorder(_root->_left);cout << _root->_key << " ";_inorder(_root->_right);}拷贝构造函数实现
由于搜索二叉树的插入顺序会对形状产生影响,我们使用递归来对其节点挨个拷贝。
//拷贝构造//拷贝构造走一个前序遍历构建,走一个递归。每前序遍历一个节点就新建一个节点BSTree(const BSTree<K>& t2){_root = Copy(t2._root);}// 1.终止条件?走到空结束// 2.这次递归应该完成的任务?创建节点,// 3.返回的信息?返回节点的指针,空反指针并将节点链接起来//Node* Copy(Node* root){if (root == nullptr)return nullptr;//这层的任务,新建节点。Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}析构函数实现
//析构函数~BSTree(){Destory();_root = nullptr;}//销毁void Destory(){while (_root)erase(_root->_key);}
赋值重载
同vector一样,我们使用摇人打工法实现赋值重载。
BSTree<K>& operator = (const BSTree<K> t){if (t == this)return *this;swap(_root, t._root);return *this;}那么以上就是一个具有最基本功能的搜索二叉树了,接下来我们尝试实现一下其KV结构。
KV结构,也就是类似于Pair的结构,一个Key绑定对应的Val,通过对比Key来找到对应的Val。
template<class K, class V>class KVTree{public:typedef KVNode<K,V> Node;bool Insert(const K& key,const V& val){if (_root == nullptr){_root = new Node(key,val);return true;}Node* cur = _root;Node* parent = cur;while (cur){//比K小,往左子树走if (key < cur->_key){parent = cur;cur = cur->_left;}//比K大,往右子树走else if (key > cur->_key){parent = cur;cur = cur->_right;}//相等,插入不了,返回一个falseelse{return false;}}//跳出while时,也就是遇到空了,新建一个节点赋值然后链接节点if (parent->_key < key){parent->_right = new Node(key,val);}else if (parent->_key > key){parent->_left = new Node(key,val);}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){//大于就向右边找if (key > cur->_key){cur = cur->_right;}//小于就向左边查找else if (key < cur->_key){cur = cur->_left;}//相等就找着了else{return cur;}}//没找着return nullptr;}void InOrder(){Node* root = GetRoot();_inorder(root);}void _inorder(Node* _root){if (_root == nullptr)return;_inorder(_root->_left);cout << _root->_key << ":"<< _root->_val<<endl;_inorder(_root->_right);}private:Node* GetRoot(){return _root;}Node* _root = nullptr;};
借助一个统计水果出现的次数来测试一下
void TextKVtree1(){KVTree<string, int> KV;string str[] ={ "菠萝","荔枝","草莓","菠萝","菠萝" ,"西瓜" ,"草莓" ,"橙子" ,"荔枝" ,"牛油果" ,"西瓜" ,"西瓜" };for (auto& e : str){KVNode<string, int>* ret = KV.Find(e);if (ret){ret->_val++;}else{KV.Insert(e,1);}}KV.InOrder();}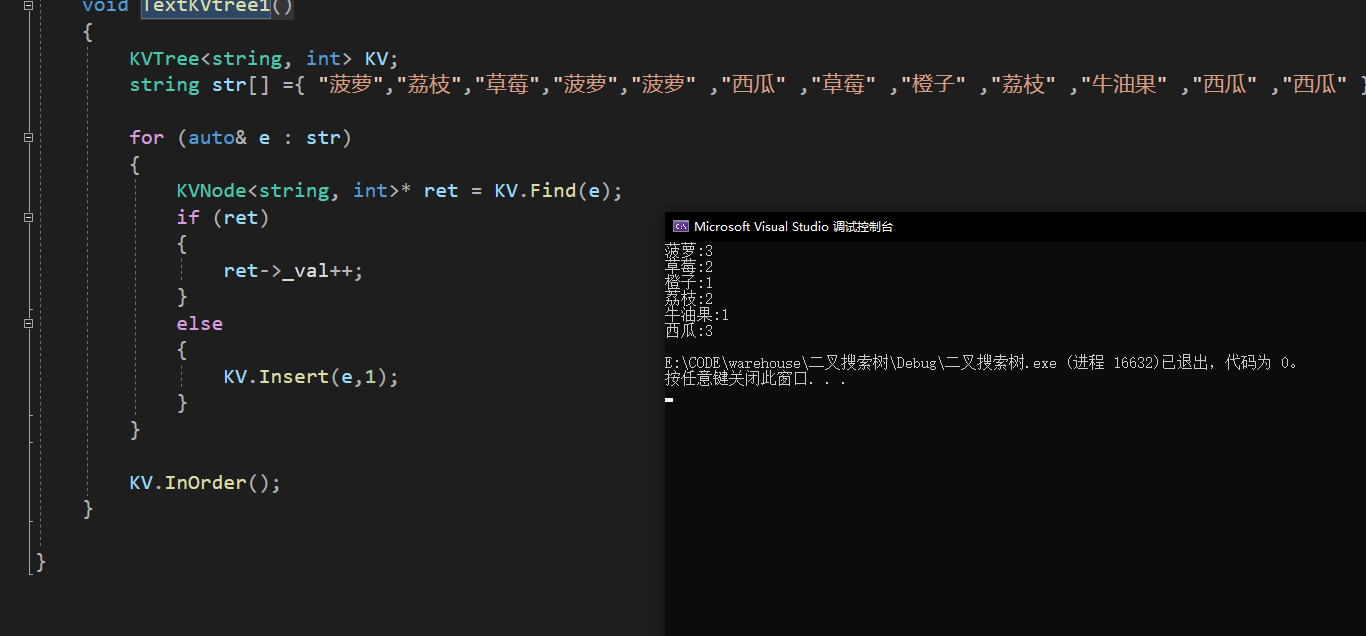
如上就是一个二叉搜索树的基本实现

相关文章:

C++13:搜索二叉树
目录 搜索二叉树概念 模拟实现搜索二叉树 插入函数实现 插入函数实现(递归) 查找函数实现 删除函数实现 删除函数实现(递归) 中序遍历实现 拷贝构造函数实现 析构函数实现 赋值重载 我们在最开始学习二叉树的时候,…...
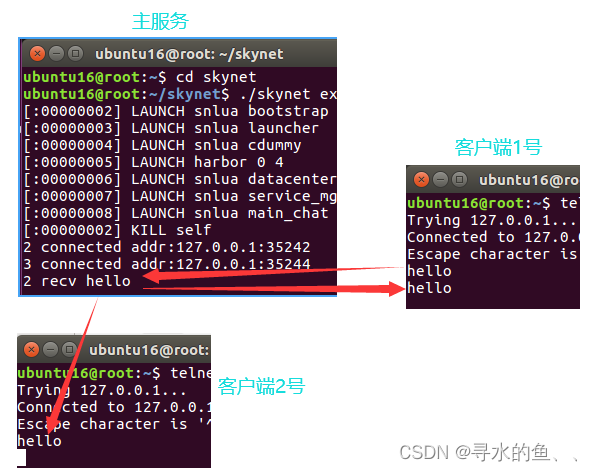
【从零开始学Skynet】基础篇(五):简易聊天室
在游戏中各玩家之间都可以进行聊天之类的交互,在这一篇中,我们就来实现一个简易的聊天室功能,这在上一篇代码的基础上很容易就能实现。1、功能需求 客户端发送一条消息,经由服务端转发,所有在线客户端都能收到…...
)
HDU - 2089 不要62(数位DP)
题目如下: 杭州人称那些傻乎乎粘嗒嗒的人为 626262(音:laoer)。 杭州交通管理局经常会扩充一些的士车牌照,新近出来一个好消息,以后上牌照,不再含有不吉利的数字了,这样一来&#x…...
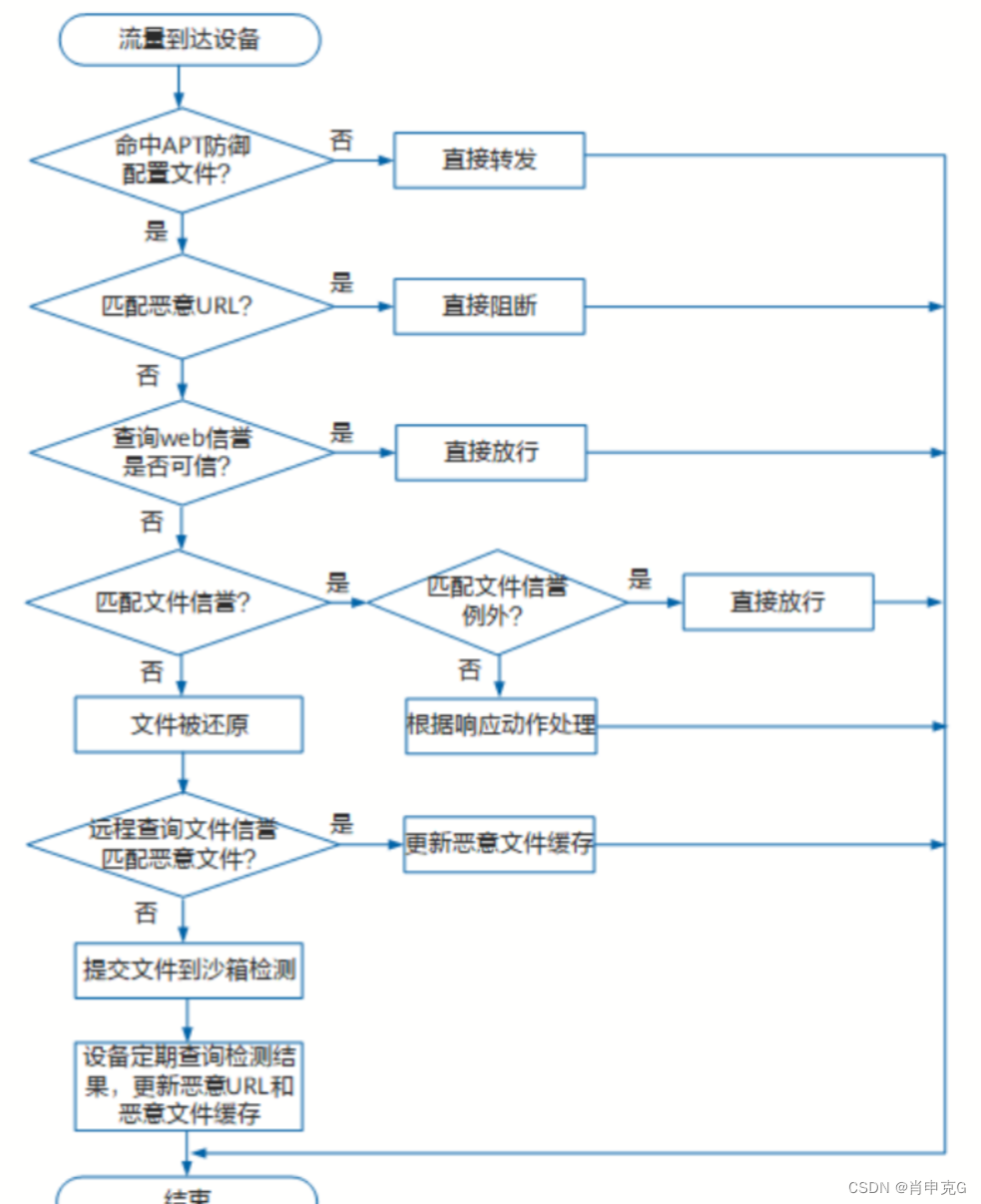
网络安全与防御
1. 什么是IDS? IDS(入侵检测系统):入侵检测是防火墙的合理补充,帮助系统对付网络攻击,扩展了系统管理员的安全管理能力,提高了信息安全基础结构的完整性。主要针对防火墙涉及不到的部分进行检测。 入侵检测主要面对的…...

【DT】蒸脱机的结构和工作原理
DT蒸脱机的结构和工作原理什么是DTDT结构图工作过程什么是DT DT 蒸脱机(DesolventazationerToaster),根据英文名可以看出来,他的作用是脱溶、烘烤。用于蒸脱湿豆粕中的溶剂。 大豆油生产工艺有2种:压榨油的加工工艺是…...

Docker管理软件
下面是一些常见的Docker管理软件 Portainer Portainer是一个轻量级的Docker管理界面,可以以用户友好的方式显示Docker环境的状态。它提供了仪表板、容器、镜像、卷、网络等功能。 Rancher Rancher是一个开源的Docker容器管理平台,支持多个主机和集群…...
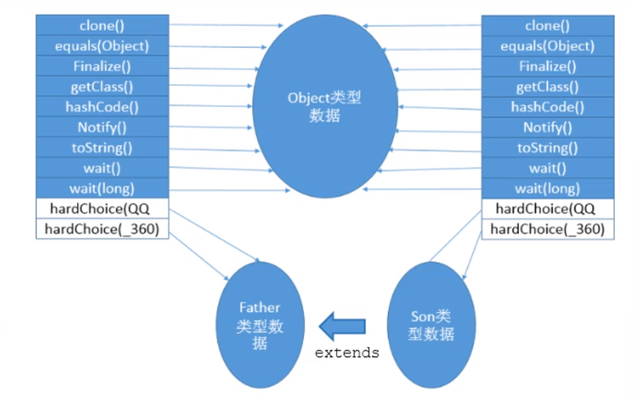
关于运行时内存数据区的一些扩展概念
栈顶缓存技术(Top-of-Stack Cashing) 前面提过,基于栈式架构的虚拟机所使用的零地址指令更加紧凑,但完成一项操作的时候必然需要使用更多的入栈和出栈指令,这同时也就意味着将需要更多的指令分派(instruction dispatc…...
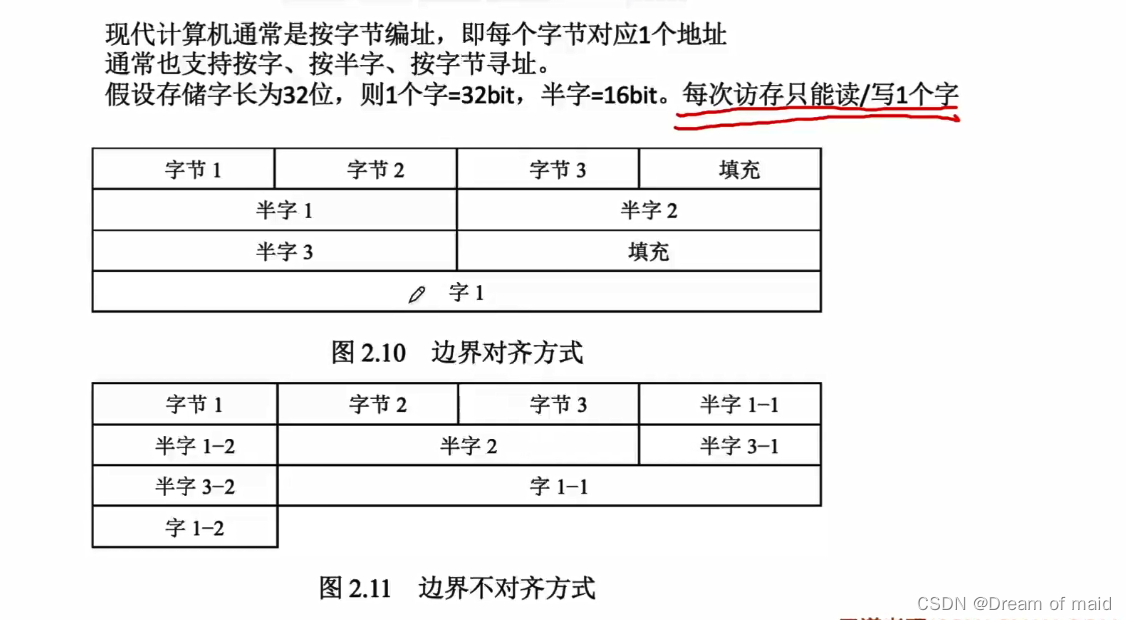
计算机组成原理第二章数据的表示与运算(中)
提示:且行且忘且随风,且行且看且从容 文章目录前言2.2.0 奇偶校验码(大纲已删)2.2.1 电路的基本原理 加法器设计2.2.2 并行进位加法器2.2.3 补码加减运算器2.2.4 标志位的生成2.2.5 定点数的移位运算2.2.62.2.6.1 原码的乘法运算2.2.6.2 补码的乘法运算2…...

我的第一台电脑的故事
第一台电脑啊,多么遥远的故事了,又似乎就在眼前。今天重回往事,就简单记录一下吧。 🌱缘起 那是初一,至今已13年,遂觉遥远,而又是立志我学习的起点,至今还在校园,又觉就…...

【1041. 困于环中的机器人】
来源:力扣(LeetCode) 描述: 在无限的平面上,机器人最初位于 (0, 0) 处,面朝北方。注意: 北方向 是 y 轴的正方向。南方向 是 y 轴的负方向。东方向 是 x 轴的正方向。西方向 是 x 轴的负方向。 机器人可…...

几何算法——4.交线(intersection curve)的表达与参数化、微分性质
几何算法——4.曲面求交的交线(intersection curve)的表达与参数化、微分性质1 关于曲面求交的交线表达2 交线的微分性质3 交线的参数化4 修正弦长参数化的微分性质1 关于曲面求交的交线表达 两个曲面求交,比较经典的方法是用跟踪法…...
【GPT】让你事半功倍特别好用的5个GPT工具
文章目录前言一、现在还能开通ChatGPT4.0吗?二、推荐五款与ChatGPT的相关实用工具1.一款浏览器插件:ChatGPT for Google2.一款生成图片的AI工具:midjourney3.推荐两款AI自动生成PPT:闪击PPT、mindshow4.识别PFD文件内容对话&#…...

人工智能大模型多场景应用原理解析
前言 在上篇文章《人工智能大模型之ChatGPT原理解析》中分享了一些大模型之ChatGPT的核心原理后,收到大量读者的反馈,诸如:在了解了核心原理后想进一步了解未来的发展趋势(比如生成式人工智能和元宇宙能擦出什么样的火花?),大模型…...
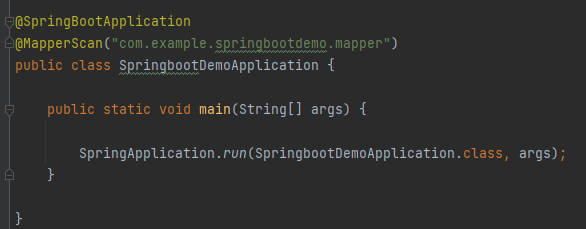
SpringBoot默认包扫描机制与默认配置文件
文章目录一、SpringBoot默认包扫描机制 - 示例二、SpringBoot默认扫描包机制 - 原理三、SpringBoot手动扫描包机制 - 原理&示例四、ComponentScan与MapperScan五、SpringBoot默认配置文件一、SpringBoot默认包扫描机制 - 示例 默认情况下,扫描启动类同级及其子…...
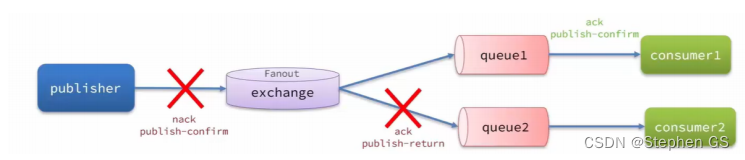
RabbitMq 消息可靠性问题(一) --- publisher发送时丢失
前言 消息从生产者发送到exchange, 再到 queue, 再到消费者。这个过程中有哪些有消息丢失的可能性呢? 发送时丢失: 生产者发送的消息未送达 exchange消息到达 exchange 后未到达 queue MQ 宕机,queue将消息丢失consumer 接收到消息后未消费…...

Java初识泛型
目录 一、包装类 1、基本数据类型和对应的包装类 2、装箱和拆箱 3、自动装箱和自动拆箱 二、什么是泛型 三、引出泛型 1、泛型的语法 四、泛型类的使用 1、语法 2、示例 3、类型推导(Type Inference) 六、泛型如何编译的 1、擦除机制 2、为什么不能实例化泛型类…...
寸照换底色技巧大全,超详细图文教程
在日常的设计工作中,我们常常需要将图片的背景色进行修改,以适应不同的场景和需求。其中最常用的方法就是寸照换底色技巧。本文将为大家介绍一些常见的寸照换底色技巧,并提供超详细的图文教程,帮助大家轻松完成这项任务。 一、使…...

这篇文章价值很大:股票历史分时成交数据怎么简单获取?【干货】
文章目录前言一、准备二、使用步骤1.引入库2,使用这个API查询历史分时数据:3.查询完整历史分时数据4.其他查询方法参数格式:[(市场代码, 股票代码), ...]参数:市场代码, 股票代码, 文件名, 起始位置, 数量参数:市场代码…...
muduo源码剖析--Buffer
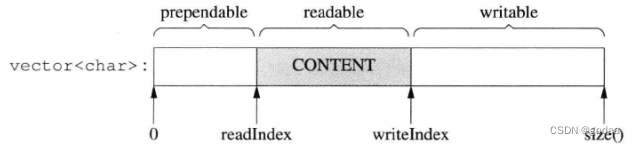
Buffer类 Buffer类是自定义处理数据输入缓冲的类,底层是vector< char >,通过readIdx和writeIdx将缓冲区分为3个部分,第一部分是预留的8字节已经读出的缓冲区字节数、第二部分是还未读出的部分、第三部分是可写的部分。 Buffer类的设计…...

AI人工智能简介和其定义
全称:人工智能(Artificial Intelligence) 缩写:AI / ai 人工智能研究 亦称智械、机器智能,指由人制造出来的可以表现出智能的机器。通常人工智能是指通过普通计算机程序来呈现人类智能的技术。该词也指出研究这样的智…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
