计算机组成原理第二章数据的表示与运算(中)
提示:且行且忘且随风,且行且看且从容
文章目录
- 前言
- 2.2.0 奇偶校验码(大纲已删)
- 2.2.1 电路的基本原理 加法器设计
- 2.2.2 并行进位加法器
- 2.2.3 补码加减运算器
- 2.2.4 标志位的生成
- 2.2.5 定点数的移位运算
- 2.2.6
- 2.2.6.1 原码的乘法运算
- 2.2.6.2 补码的乘法运算
- 2.2.7.1
- 原码的除法运算
- 2.2.7.2 补码的除法运算
- 2.2.8 c语言的类型转换
- 2.2.9 数据的存储和排列
前言
2.2.0 奇偶校验码(大纲已删)
在有效信息位的首部或者尾部加上一位奇偶校验位
奇校验码:整个校验码(有效信息位和校验位) 中“1”的个数为奇数个
偶校验码:整个校验码(有效信息位和校验位)中“1”的个数为偶数
其实也就是数给定的编码中1的个数, 若是奇校验码,其中有效信息码中1的个数为奇数个,则校验位添加0 若是有效信息码中1的个数为偶数个,则校验位添加1,
偶校验的硬件实现,各信息进行异或(模2加)运算,得到的结果即为偶校验位,然后进行偶校验(所有位进行异或,若结果为1,说明出错,但是若是同时有两个bit发生错误,则进行偶校验也是不能发现错误的)
2.2.1 电路的基本原理 加法器设计
这里主要讲三个部分,算数逻辑单元的作用,大致原理,电路基础知识,加法器的实现,与类似C语言&& 表达式Y=A*B “或”类似“||” 表示式Y=A+B,但是要注意优先级“与”是大于“或”的,同时满足分配律以及结合律如A(C+D)=AC+AD ,再如ABC=A(BC),异或相同是零,相异是一 同或 相同是一,相异是零,与异或正好相反
一位全加器两个本位和一个来自低位的进位可以确定本位的和并且也能确定应该向高位进一个什么样的值,
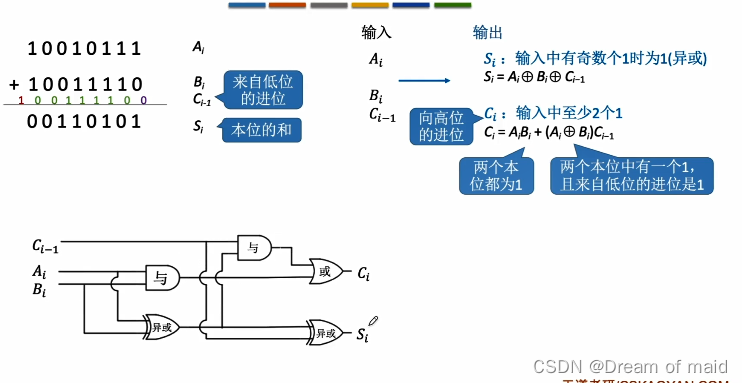
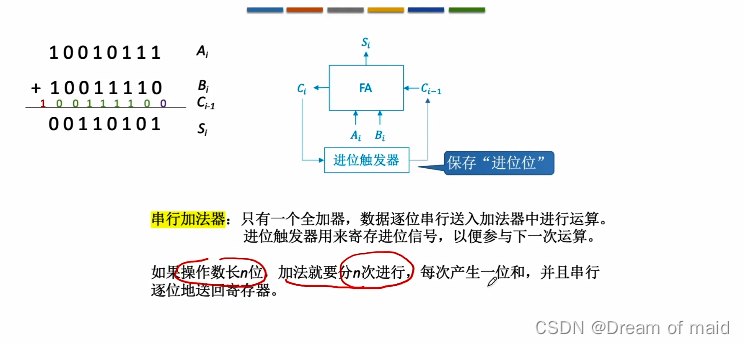
串行加法器
只有一个全加器,数据逐位串行送入加法器中进行运算,进行触发器用来寄存进位信号,以便参与下一次运算,如果操作数长n位,加法就要分n此进行,每次产生一位和,并且串行逐位地送回寄存器,所以这张串行加法器的效率较低
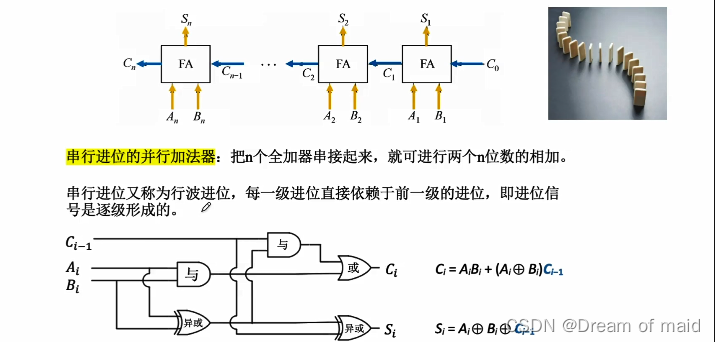
并行加法器
把n个全加器串联起来,就可以进行两个n位数的相加,串行又称为行波进位,每一级进行直接依赖于前一级的进位,既进行信号是逐级形成的,所以这种加法器的快慢却决于每一位进位的速度
本节总览
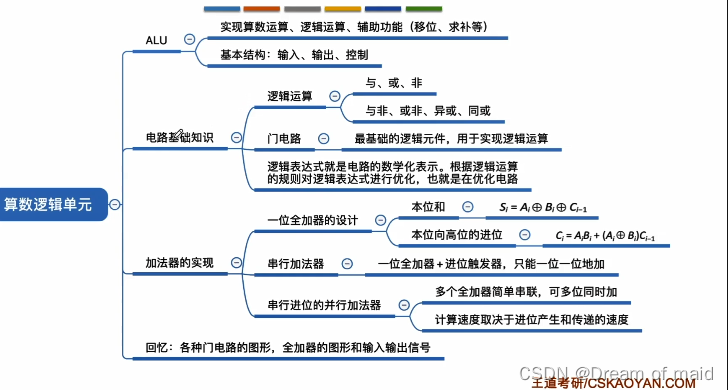
2.2.2 并行进位加法器
上述的时候我们讲过 速度很大程度上取决于进位的速度,这里我们可以发现进位的表达式又可以用更低一位的进位表达,这里也就是数学中的递推法 最终我们发现每一级是可以使用C0表示的,也就意味着我们可以直接算出每一个全加器的值,也就意味着每一个进位几乎都是同时产生的,但是这样也有一个缺点就是会导致设计的电路越来越复杂,所以通常是有四个全加器和一些运算逻辑组成
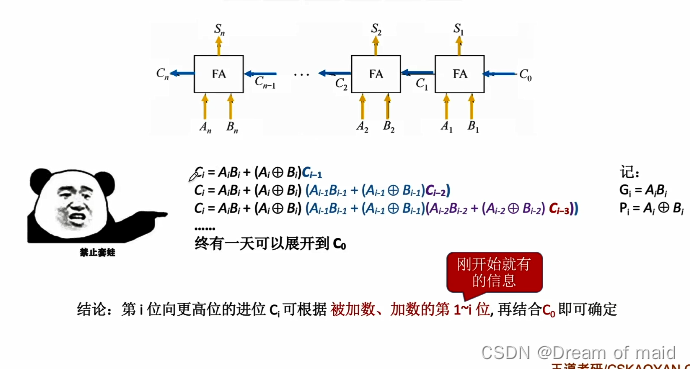
2.2.3 补码加减运算器
也就是从硬件的角度来看补码的加减运算是如何实现的,如下图,若是我们进行的是X+Y 则此时Sub也就是0 此时控制多路选择器 Y的值直接通过,若是X-Y 此时Sub也就是1,此时控制多路选择器打开1这个开关,而Y也要进行非操作,此时再加上sub 中的这个一,也就实现了减法变加法(全部位取反,末位值加一)
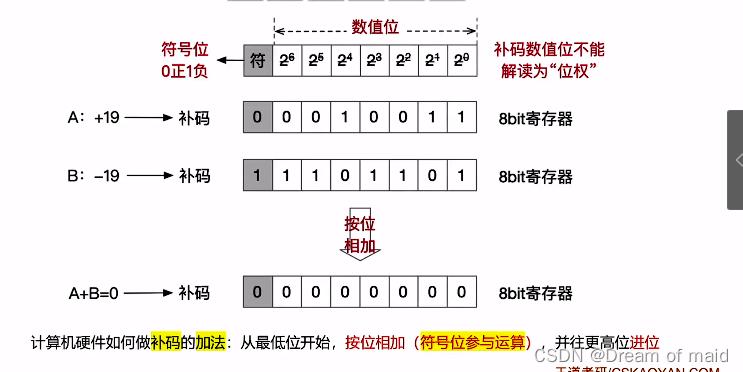
入下 计算机的底层逻辑在处理加法或者减法的时候是,无论是有符号数还是无符号数都是通过同一个电路来处理的,但是最后我们判断是否溢出的时候,有符号数的判断逻辑和无符号数的判断逻辑是存在显著的区别的


2.2.4 标志位的生成
两个nbit的数相加,除了生成一个nbit的值外 同时也会生成四个标志位如下

2.2.5 定点数的移位运算
移位:通过改变各个数码位和小数点的相对位置,从而改变数码位的位权,可用移位运算实现乘法和除法,原码的算数移位——符号位保持不变,仅对数值位进行移动,右移:高位补0,低位舍弃,若舍弃的位=0,则相当于/2 若舍弃的位!=0 则会丢失精度,其实这些也是可以理解的,原码到反码的过程中有一个是全部取反,自然左边高位是补一,而反码又要加一,自然作用到补码上低位也就是补零
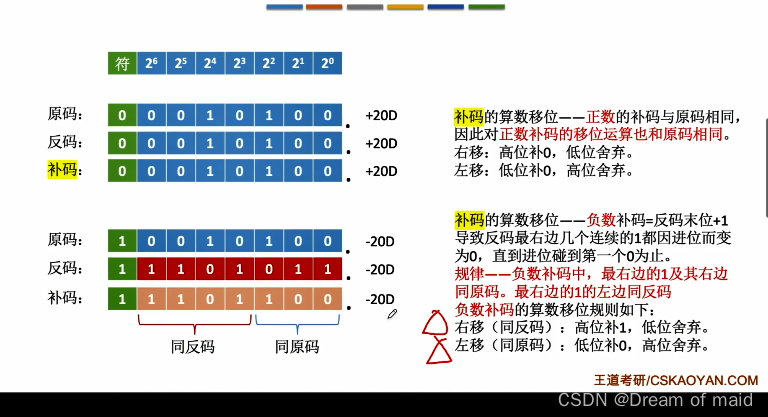
循环移位
不带进位位:用移出的位补上空缺,带进位位,移出的位放到进位位,原进位位补上空缺
2.2.6
2.2.6.1 原码的乘法运算
这节主要讲三个问题,乘法运算的实现思想,原码的一位乘法,补码的一位乘法
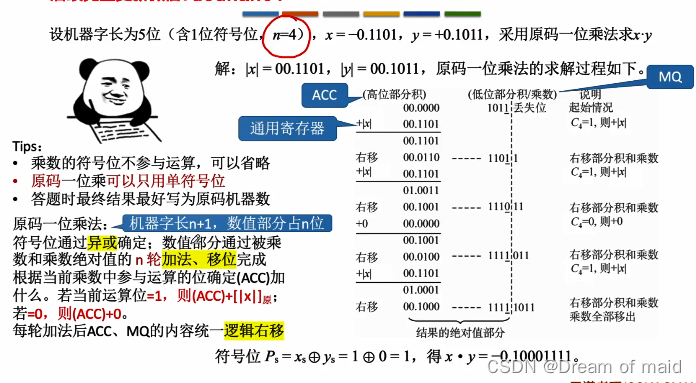
乘法运算的实现思想将乘数拆成多个数相加,再用被乘数分别与这些乘数进行相乘再相加,但是这里考虑到机器实现有三个问题,1,实际数字有正负,符号位如何处理?,2,乘积的位数扩大一倍,如何处理?,3,4个位积都要保存下来最后统一相加?
问题一:符号位单独处理,符号位=A异或B
问题二:先加法再移位 重复n次,当前位=1,则ACC加上被乘数,当前位=0,则ACC加上0,每次乘完之后 在进行移位,然后乘积高位往右移动,继续看乘数的乘低位,为1则与乘积高位相加,结果放在乘积高位中,在移动,再继续看乘积低位
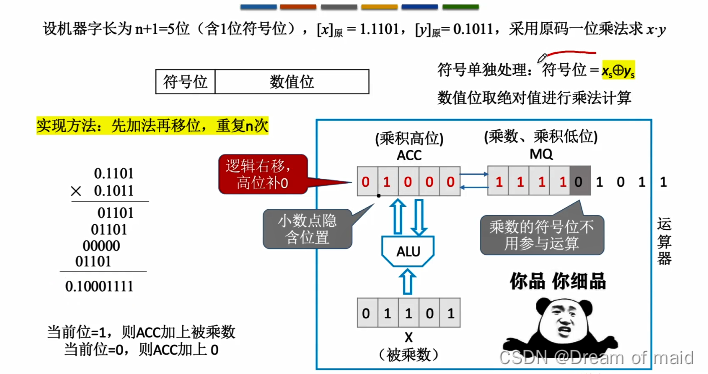 问题三:你会发现这里的结果不是每一个算出来 然后相加 而是一位算出来就放在ACC与MQ中了
问题三:你会发现这里的结果不是每一个算出来 然后相加 而是一位算出来就放在ACC与MQ中了
这里使用的是双符号位,但是使用单符号位也不会出错,至于这里为什么使用双符号位,可能是因为补码的乘法一定要使用双符号位,这里可能是与补码保持统一
2.2.6.2 补码的乘法运算
和原码的移位加法相似,但是还需要多来一次加法,最后的这一次加法会让乘数的符号位也参与运算,只有加法没有移位,如下图MQ红色部分既是这里所说的辅助位,所有寄存器的长度一般都是统一的,所以这里的补码采用的是双符号位的形式,
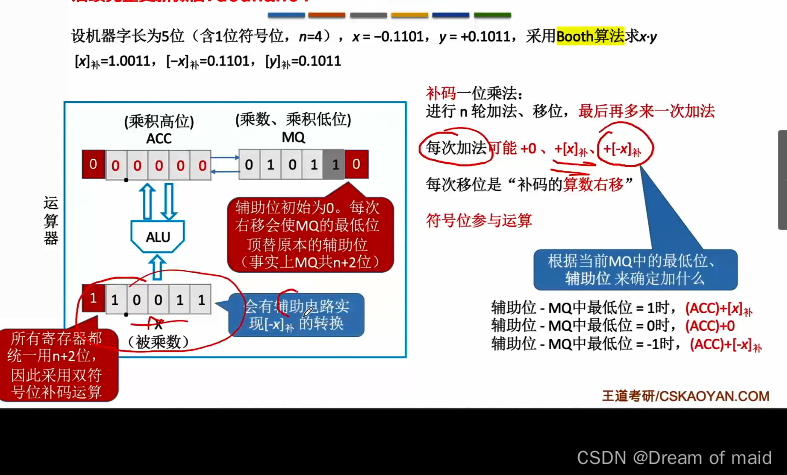
如对下图的解析,第一步的时候,辅助位-MQ中的最低位为-1,这个时候加上乘数的补码 然后ACC和MQ统一右移,符号位不动,数值位右移,正数右移补0 负数右移补1(符号位是啥就补啥),Y5是这里的辅助位,Y4是这里MQ中的最低位

知识点回顾

2.2.7.1
原码的除法运算
如下图ACC中保留的是被除数 MQ中保留的是商 通用寄存器中保留的是除数,本来我们的想法是比较ACC与通用寄存器中的值来确定商的值,但是计算机很傻,会先默认商一,若是检查到ACC中的符号位是1(负)此时也就会修改商上面的值让其为0 并且让ACC恢复原样,然后减去除数,ACC与MQ整体左移低位补零,然后依然是默认商1,若是最后一步商余数为负,也需要回复余数并商零
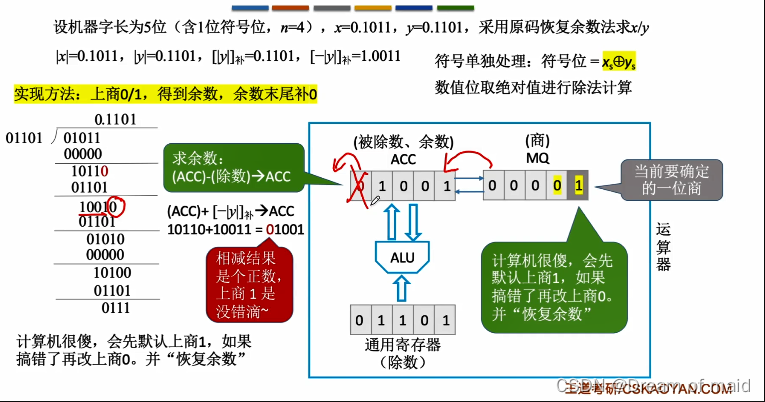
恢复余数法(手算)
根据所得余数的符号位的正负来确定商应该是0或者1
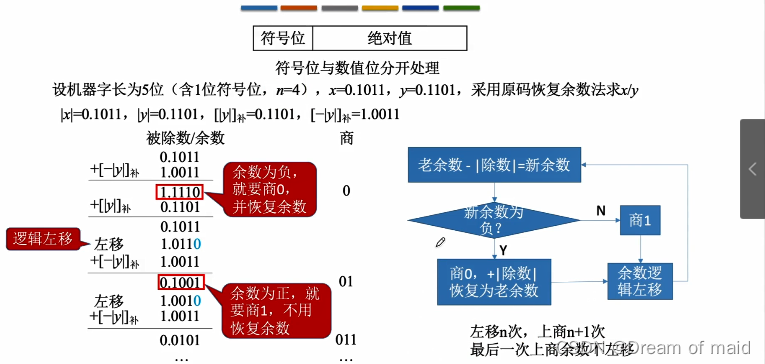
恢复余数法的改进
若余数为负,则可直接商0,并让余数左移一位再加上除数
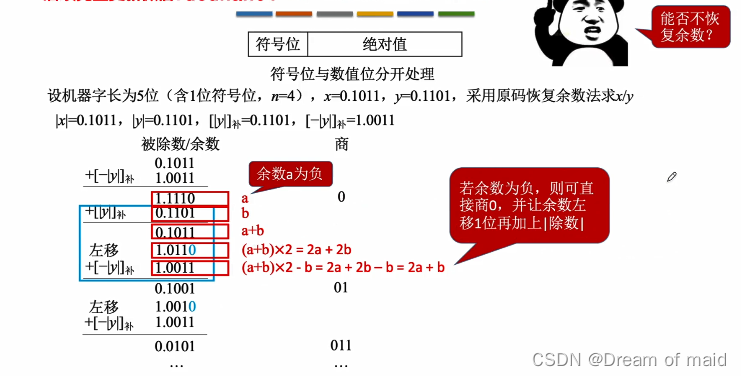
不恢复余数法(手算)
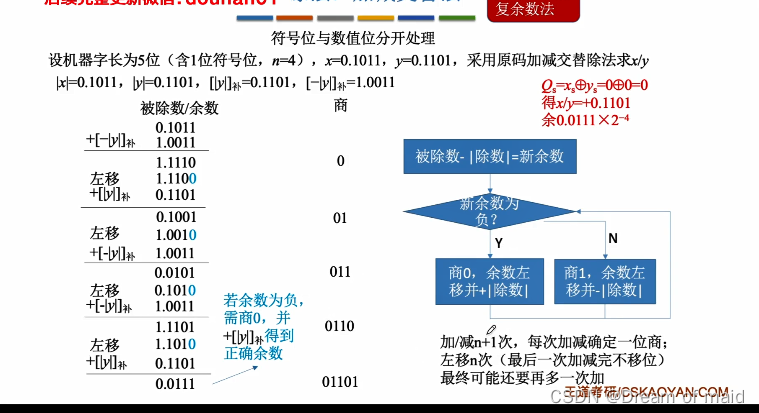
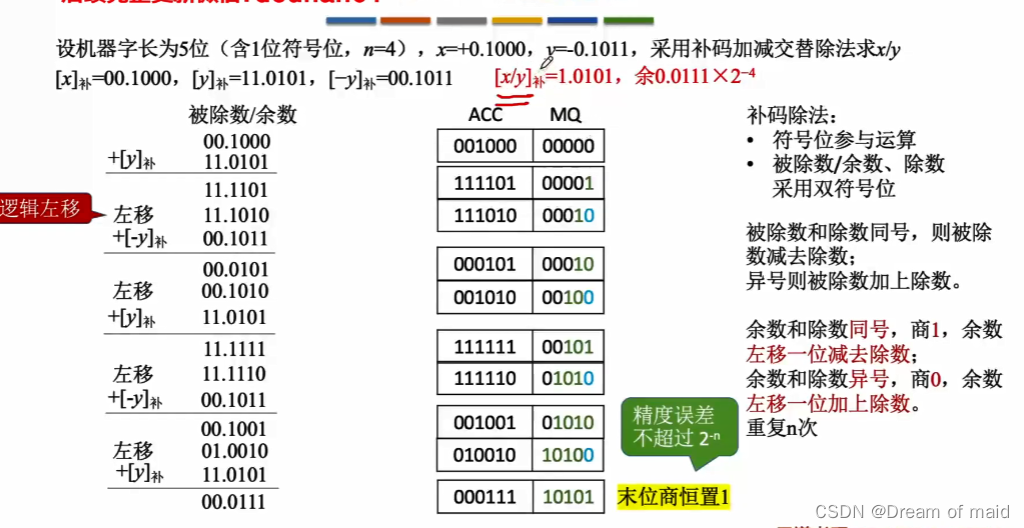
2.2.7.2 补码的除法运算
2.2.8 c语言的类型转换
C语言中定点整数是用“补码”存储的
所以进行强制转化的时候
无符号数和有符号数:不改变数据内容,改变解释方式
长整数变短整数:高位截断,保留低位
短整数变长整数:符号扩展
2.2.9 数据的存储和排列
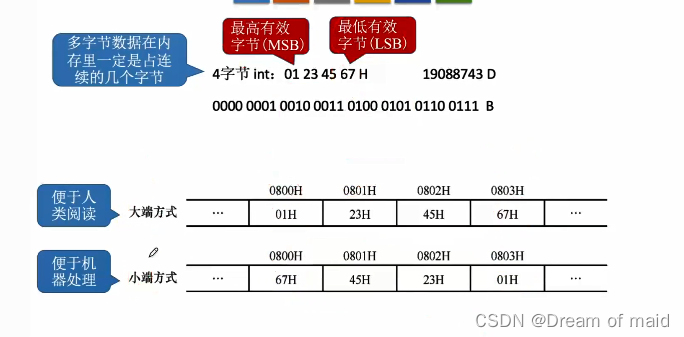
大小端模式
小段读取的方式更有利于机器的处理:计算机首先从计算机读入的最低有效字节 这样CUP在处理加法的时候,这样从低有效字节读入是有利于处理的
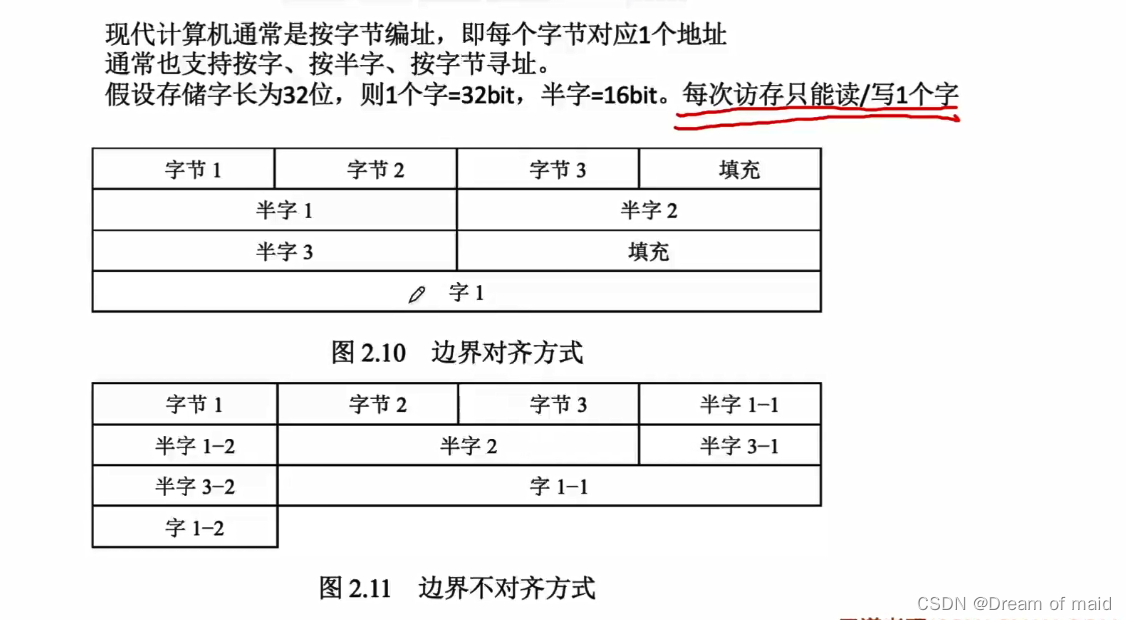
边界对齐
这个东西通常是结构体定义的时候,比如下图我们定义了三个char型变量 三个short型变量,还有一个short型变量,若是按照边界不对齐的方式,我们读取第一个short变量的时候需要两次访问并进行拼接,而上边界对齐则一次访问便可,且不需要拼接,一种空间换取时间的策略
相关文章:

计算机组成原理第二章数据的表示与运算(中)
提示:且行且忘且随风,且行且看且从容 文章目录前言2.2.0 奇偶校验码(大纲已删)2.2.1 电路的基本原理 加法器设计2.2.2 并行进位加法器2.2.3 补码加减运算器2.2.4 标志位的生成2.2.5 定点数的移位运算2.2.62.2.6.1 原码的乘法运算2.2.6.2 补码的乘法运算2…...

我的第一台电脑的故事
第一台电脑啊,多么遥远的故事了,又似乎就在眼前。今天重回往事,就简单记录一下吧。 🌱缘起 那是初一,至今已13年,遂觉遥远,而又是立志我学习的起点,至今还在校园,又觉就…...

【1041. 困于环中的机器人】
来源:力扣(LeetCode) 描述: 在无限的平面上,机器人最初位于 (0, 0) 处,面朝北方。注意: 北方向 是 y 轴的正方向。南方向 是 y 轴的负方向。东方向 是 x 轴的正方向。西方向 是 x 轴的负方向。 机器人可…...

几何算法——4.交线(intersection curve)的表达与参数化、微分性质
几何算法——4.曲面求交的交线(intersection curve)的表达与参数化、微分性质1 关于曲面求交的交线表达2 交线的微分性质3 交线的参数化4 修正弦长参数化的微分性质1 关于曲面求交的交线表达 两个曲面求交,比较经典的方法是用跟踪法…...
【GPT】让你事半功倍特别好用的5个GPT工具
文章目录前言一、现在还能开通ChatGPT4.0吗?二、推荐五款与ChatGPT的相关实用工具1.一款浏览器插件:ChatGPT for Google2.一款生成图片的AI工具:midjourney3.推荐两款AI自动生成PPT:闪击PPT、mindshow4.识别PFD文件内容对话&#…...

人工智能大模型多场景应用原理解析
前言 在上篇文章《人工智能大模型之ChatGPT原理解析》中分享了一些大模型之ChatGPT的核心原理后,收到大量读者的反馈,诸如:在了解了核心原理后想进一步了解未来的发展趋势(比如生成式人工智能和元宇宙能擦出什么样的火花?),大模型…...
SpringBoot默认包扫描机制与默认配置文件
文章目录一、SpringBoot默认包扫描机制 - 示例二、SpringBoot默认扫描包机制 - 原理三、SpringBoot手动扫描包机制 - 原理&示例四、ComponentScan与MapperScan五、SpringBoot默认配置文件一、SpringBoot默认包扫描机制 - 示例 默认情况下,扫描启动类同级及其子…...
RabbitMq 消息可靠性问题(一) --- publisher发送时丢失
前言 消息从生产者发送到exchange, 再到 queue, 再到消费者。这个过程中有哪些有消息丢失的可能性呢? 发送时丢失: 生产者发送的消息未送达 exchange消息到达 exchange 后未到达 queue MQ 宕机,queue将消息丢失consumer 接收到消息后未消费…...

Java初识泛型
目录 一、包装类 1、基本数据类型和对应的包装类 2、装箱和拆箱 3、自动装箱和自动拆箱 二、什么是泛型 三、引出泛型 1、泛型的语法 四、泛型类的使用 1、语法 2、示例 3、类型推导(Type Inference) 六、泛型如何编译的 1、擦除机制 2、为什么不能实例化泛型类…...
寸照换底色技巧大全,超详细图文教程
在日常的设计工作中,我们常常需要将图片的背景色进行修改,以适应不同的场景和需求。其中最常用的方法就是寸照换底色技巧。本文将为大家介绍一些常见的寸照换底色技巧,并提供超详细的图文教程,帮助大家轻松完成这项任务。 一、使…...

这篇文章价值很大:股票历史分时成交数据怎么简单获取?【干货】
文章目录前言一、准备二、使用步骤1.引入库2,使用这个API查询历史分时数据:3.查询完整历史分时数据4.其他查询方法参数格式:[(市场代码, 股票代码), ...]参数:市场代码, 股票代码, 文件名, 起始位置, 数量参数:市场代码…...
muduo源码剖析--Buffer
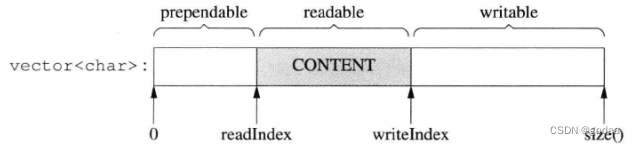
Buffer类 Buffer类是自定义处理数据输入缓冲的类,底层是vector< char >,通过readIdx和writeIdx将缓冲区分为3个部分,第一部分是预留的8字节已经读出的缓冲区字节数、第二部分是还未读出的部分、第三部分是可写的部分。 Buffer类的设计…...

AI人工智能简介和其定义
全称:人工智能(Artificial Intelligence) 缩写:AI / ai 人工智能研究 亦称智械、机器智能,指由人制造出来的可以表现出智能的机器。通常人工智能是指通过普通计算机程序来呈现人类智能的技术。该词也指出研究这样的智…...
python数据清洗
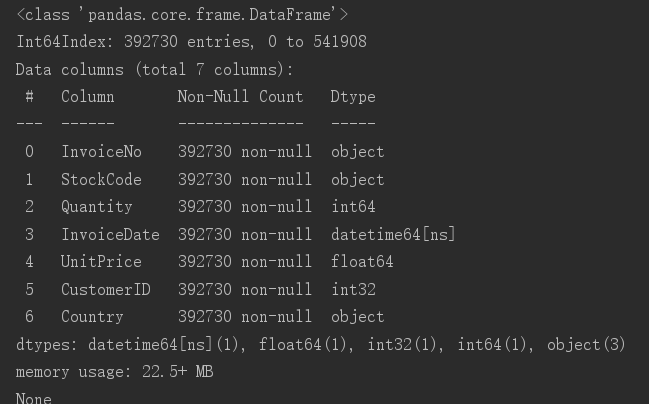
数据清洗包括:空值,异常值,重复值,类型转换和数据整合这里数据清洗需要用到的库是pandas库,下载方式还是在终端运行 : pip install pandas.首先我们需要对数据进行读取import pandas as pddata pd.read_cs…...
 方法、Python3 os.read() 方法)
Python3 os.makedirs() 方法、Python3 os.read() 方法
Python3 os.makedirs() 方法 概述 os.makedirs() 方法用于递归创建目录。像 mkdir(), 但创建的所有intermediate-level文件夹需要包含子目录。 语法 makedirs()方法语法格式如下: os.makedirs(path, mode0o777)参数 path -- 需要递归创建的目录。 mode -- 权限…...
【Linux安装数据库】Ubuntu安装mysql并连接navicat
Linux系统部署Django项目 文章目录Linux系统部署Django项目一、mysql安装二、mysql配置文件三、新建数据库和用户四、nivacat链接mysql一、mysql安装 linux安装mysql数据库有很多教程,根据安装方式不同,相关的步骤也不同。可以参考:【Linux安…...

GaussDB工作级开发者认证—第一章GaussDB数据库介绍
一. GaussDB概述 GaussDB是华为基于openGauss自研生态推出的企业级分布式关系型数据库。具备企业级复杂事物混合负载能力,同时支持分布式事务强一致性,同城跨AZ部署,数据0丢失,支持1000的计算节点扩展能力,4PB海量存储…...

阿里张勇:所有行业都值得用大模型重新做一遍!
数据智能产业创新服务媒体——聚焦数智 改变商业“2023阿里云峰会”于4月11日在北京国际会议中心隆重召开,本次峰会以" 与实俱进 为创新提速!"为主题,阿里巴巴集团董事会主席兼首席执行官张勇、阿里云智能集团首席技术官周靖人、…...
)
ES6(字符串的扩展与新增方法)
字符串的扩展与新增方法 1. 模板字符串 模板字符串解决了之前的字符串拼接 ESC下那个键:反引号()包裹>替换引号 ${变量名/表达式/函数}>替换引引加加导致的代码冗余 //ES5(引引加加) $(#result).append(There are <b> basket.c…...

rk3568点亮LCD(lvds)
rk3568 Android11/12 适配 lvds 屏 LVDS(Low Voltage Differential Signal)即低电压差分信号。1994年由美国国家半导体(NS)公司为克服以TTL电平方式传输宽带高码率数据时功耗大、电磁干扰大等缺点而研制的一种数字视频信号传输方…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
