数据结构——排序(4)
作者:几冬雪来
时间:2023年4月12日
内容:数据结构排序内容讲解
目录
前言:
1.快速排序中的递归:
2.小区间优化:
3.递归改非递归:
4.归并排序:
5.归并排序的非递归形式(框架):
结尾:
前言:
在前一篇博客中我们对快速排序的代码进行了一步优化,将它优化出来了3种方法——随机找key法,三数取中法和前后指针法。而在今天,我们则在已经优化过的基础上,对我们的代码进行进一步的优化。

1.快速排序中的递归:
在我们之前书写快速排序的时候,每次都是先写一趟快速排序,而后再使用递归的方法让我们的数组通过几次快速排序后一步步变得有序。而我们的这个递归的行为则类似我们的二叉树的操作,越往下走递归的次数越多。
而在我们二叉树的那个板块曾经就有说明过,当我们递归次数很多的时候,最后一层的递归出来的结果个数是我们总数的一半,往上到倒数第二层是1/4,再然后是1/8。
那么在这里就有人提了一个建议,就是在我们快速排序排到最后倒数第4层的时候我们就不再继续往下递归下去了,之后无序的数组我们用直接插入排序来将其变得有序,这样子做就可以大大的减少我们的递归的次数。
这种方法就被我叫做——小区间优化。
2.小区间优化:
最小区间法,顾名思义就是当我们的区间变得较小的时候,这里用其他的排序来代替我们的快速排序。那么在这里,我们就将它们的代码写出来。
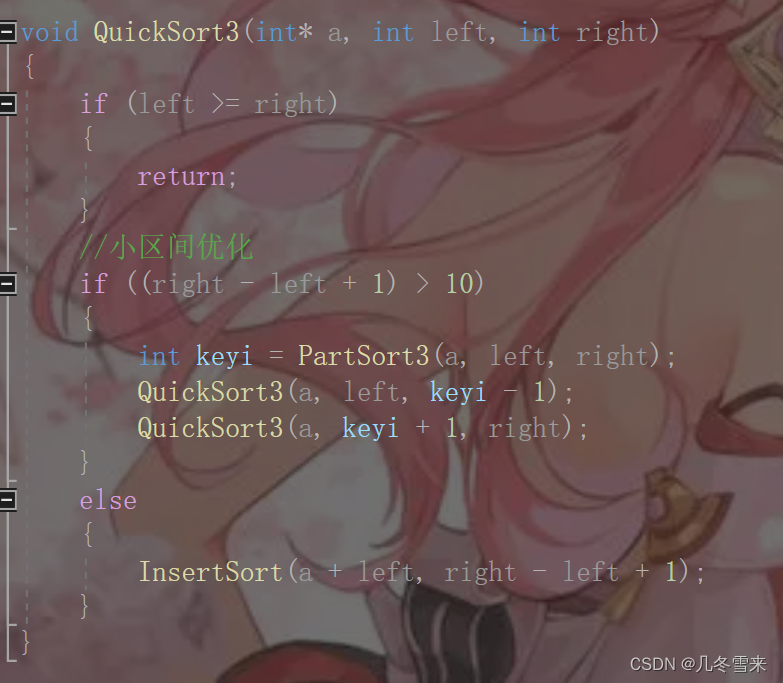
这里就是我们的小区间优化法,在这里我们有需要小心的地方,也存在着我们可以普及的内容,接下来我们就来一一细说一下。
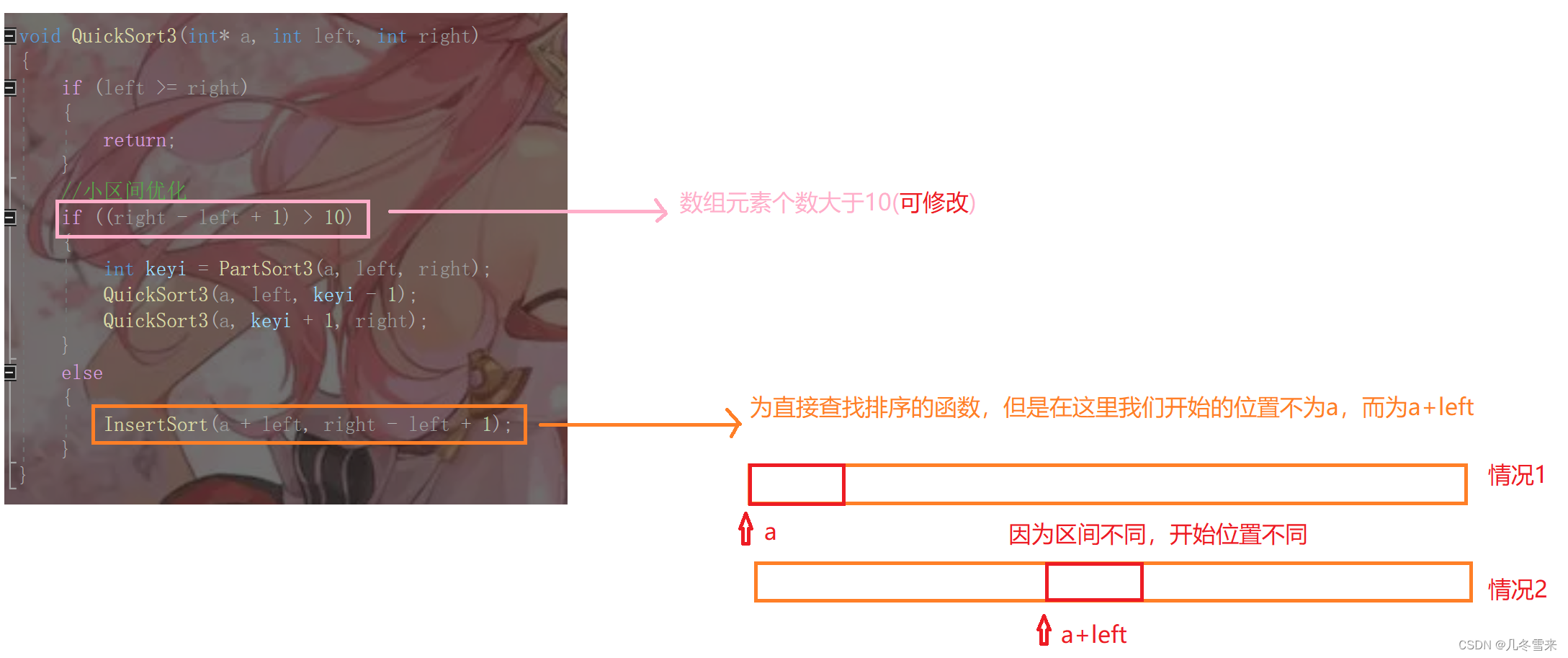
在这里我们的元素的个数是可以进行修改的。这里的大于10也可以修改为大于20或者是50,但是如果在这里进行了修改的话,我们的小区间优化法可能会适得其反。
这里要注意的是,如果区间个数过多,可能会导致这里小区间优化法的运行时间比没有小区间优化法的时间要长。且原数组元素个数少的话,小区间优化法的优化程度及其有限,当原数组的元素个数多的时候,小区间优化法才能更好的表现出来它的优势。
但是在这里我们不单单是讲小区间优化法的问题,我们是要依靠它来引出一个新的问题。
3.递归改非递归:
因为我们的快速排序所运用的方法是递归,所以这里就牵扯出来一个经典的问题——栈溢出。当我们的递归次数过多的时候,哪怕我们的代码是对的,但是它在debug中依旧也是跑不起来。栈的内存满了,我们的代码也会调试不起来,因此针对程序员而言,如果某个程序的递归没问题我们就不需要管它,相反如果出现问题的话,我们要学会将我们的递归改为非递归。
而在这里我们用到的知识则是栈板块的知识。
首先我们要把栈的头文件和.c文件一起复制到我们当前文件中。接下来就要开始我们非递归的操作了。这里要用循环来代替我们的递归,第一个要想到的是,在递归中我们递归的是什么东西,而在快排当中我们递归的对象是区间(对象不是数组因为数组不在栈中)。 因此我们的栈也要存区间。
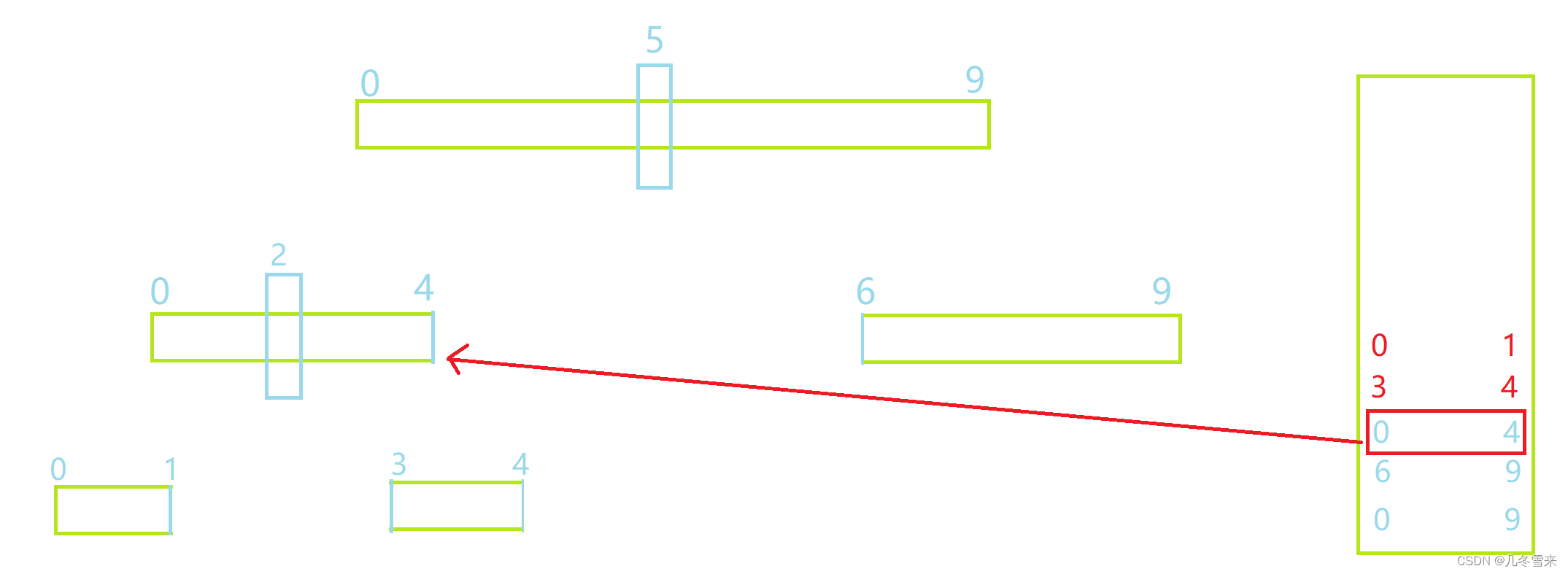
这就是我们非递归形式的快速排序的操作过程,第一次先将0和9存放到栈中,然后将其取出,找到我们的key后将其分为左右区间,接下来再把6和9先存放到栈中,而后存放0和4,下来我们继续以上的操作,直到最后我们的区间只剩下一个值或者不存在就结束。

知道这些操作之后下来就是书写我们的代码了。
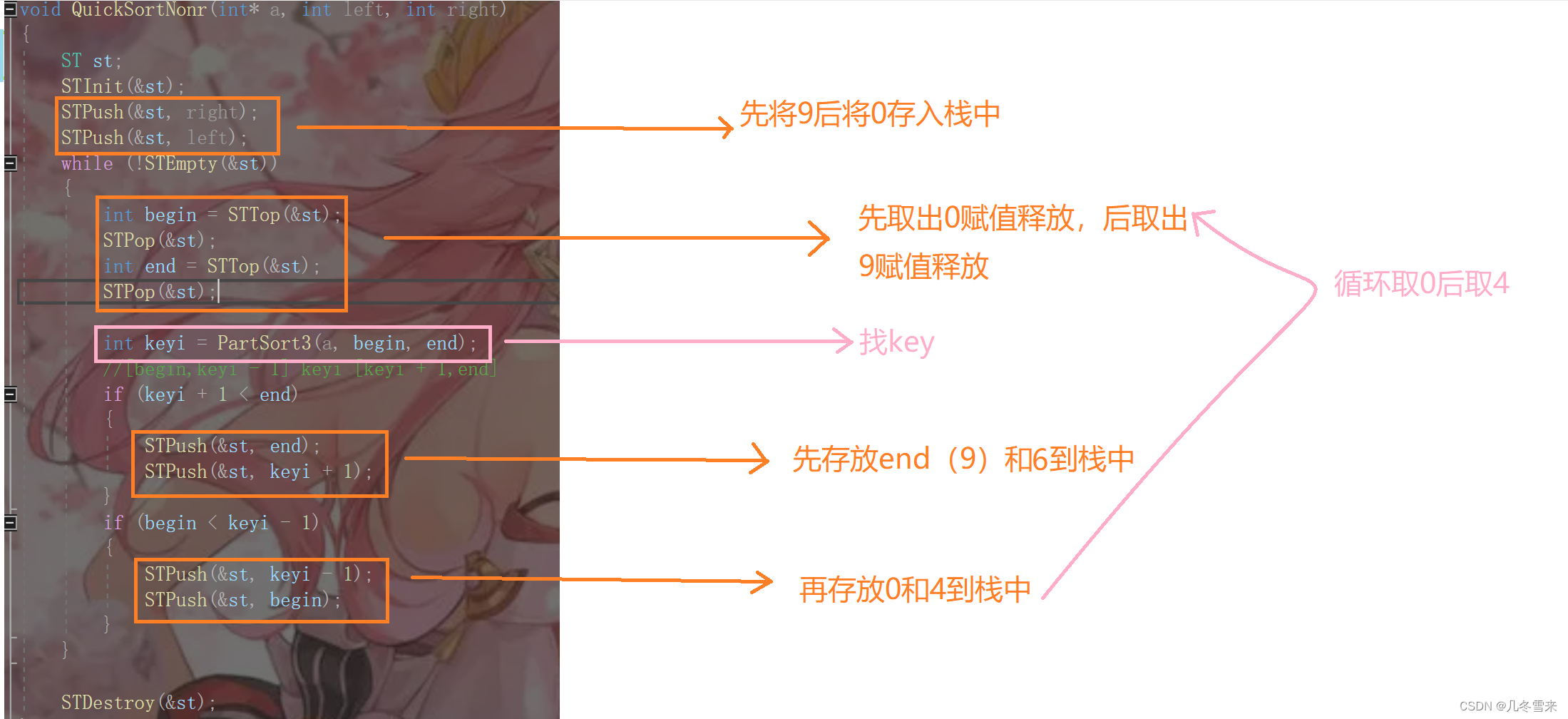
这就是我们的代码和它的讲解了,虽然这里我们的代码从递归形式改为非递归形式,但是实际上它的效率并没有什么提升,非递归形式只是防止栈溢出罢了。
4.归并排序:
接下来要讲解的排序是我们的归并排序,归并排序也是我们一种十分有效的排序方法。
接下来是我们归并排序的操作图。
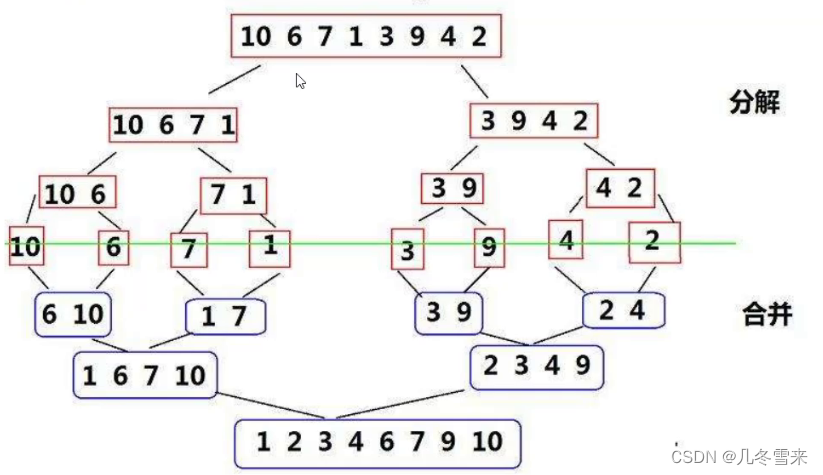
在这里我们将我们的数组拆为平均两个部分,然后判断两个部分是否有序,无序的话就继续往下拆分,直到我们拆分下最后一个数的时候,这里我们就开始回归,回归的时候我们的每个区间都会变得有序。
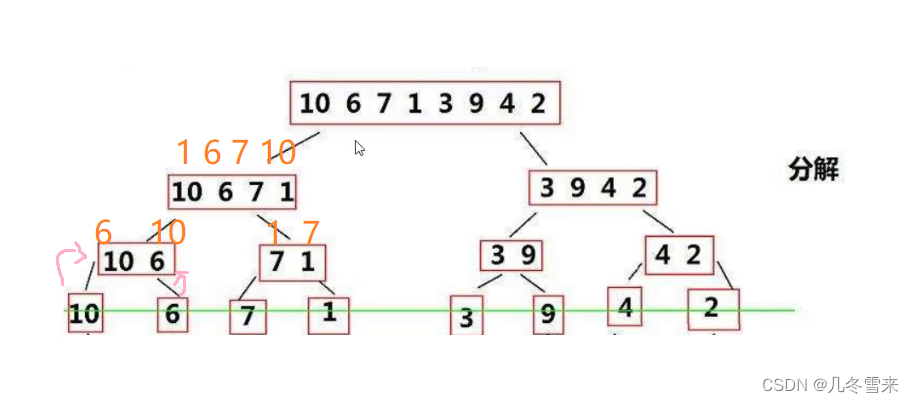
当最后我们合并剩下两个区间的时候,我们最后再把它们进行一次合并排序,最后我们的数组就可以变得有序起来了。
同样的在这里我们的归并排序的时间复杂度也为标准的O(N*logN)。因为在这里我们每层需要排序的个数都为N,并且每次排序都是将区间平均的一分为二,所以它的时间复杂度是logN。
在归并排序中有人看我们的这个图片,以为每次分解都要建立一个小数组,但是其实不是的。

在这里我们只需要一个临时数组来帮助我们进行排序,每次排序之后我们就要将我们的内容给拷贝出去。当最后归并到我们的左右都有序之后,将它拷贝回原数组中,它就有序了。接下来就是来书写我们的代码了和其解析。
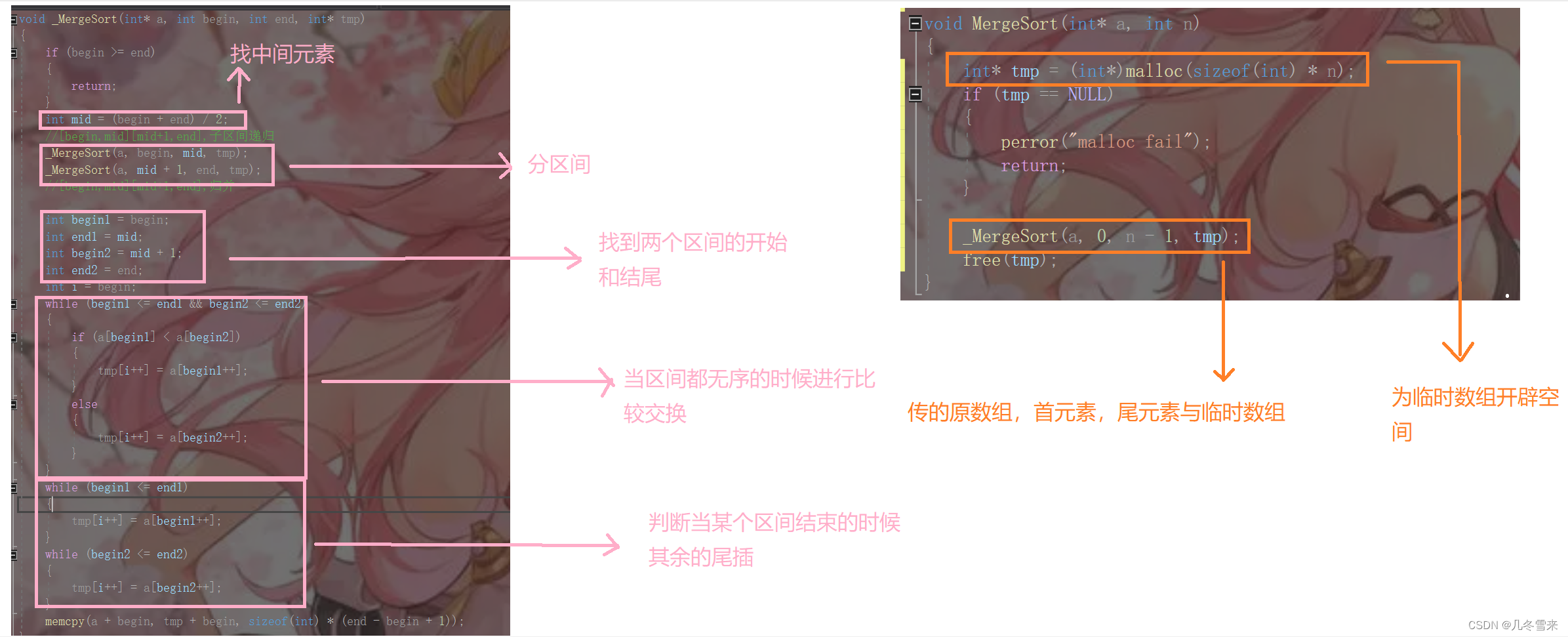
这就是我们的代码和它的解析了,这里需要注意的是,在这里我们每次递归都是要用到整个数组的元素,因此在判断那里我们需要用到等于号。
这里我们用的数组刚刚好可以被我们平均的拆分为2个大小相等的数组,如果这里数组中元素的个数是单数的话,我们的代码依旧可以跑起来吗?
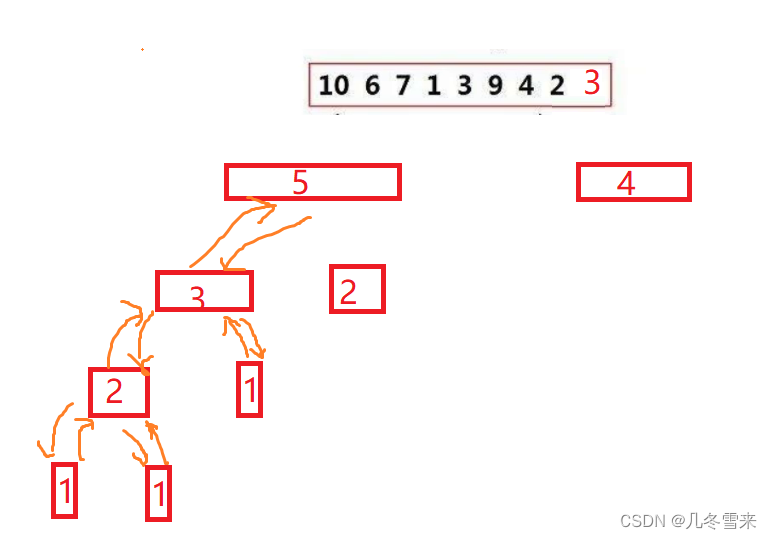
这里从结果中可以看出,哪怕我们的数组元素的个数是单数的,我们依旧可以通过这种方法对我们的数组进行排序,它并不影响我们排序的进行。
5.归并排序的非递归形式(框架):
同样的在这里,我们的归并排序也有它的非递归形式。在前面我们讲到,递归变循环我们又两种方法,一种的借助栈来进行修改,另外一种则是直接修改,而在这里归并排序的非递归形式是自己对其进行修改。
这里我们又一个方法。
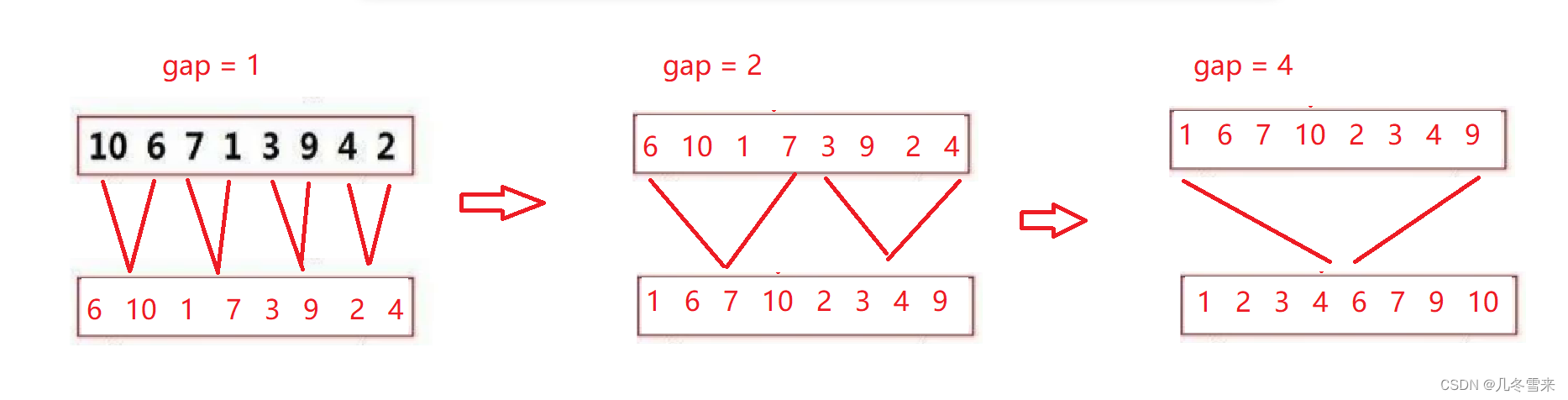
在这里我们取一个gap值,每次归并后我们的gap值增加,我们每次参与归并的元素个数也随之增加。 就类似我们上图这样,不过这种方法有需要修改的点,比如边界问题等,我们就留到下一篇博客来讲解了。
接下来我们就来浅浅的写一写我们的代码和它的解析。
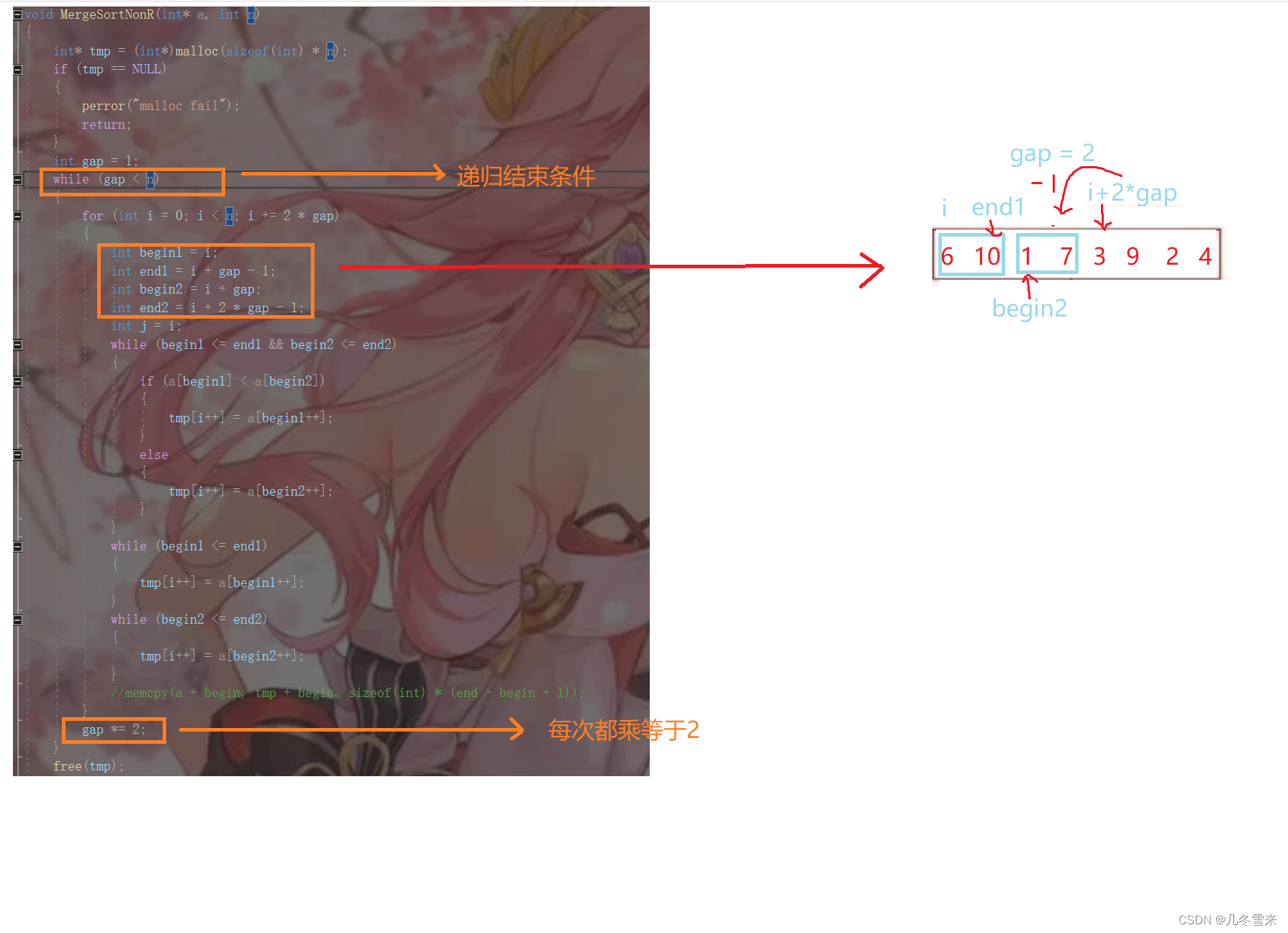
这就是我们归并排序非递归形式代码的一个大体的框架,这其中还存在着很多的问题。这些我们就留到下一篇博客再来讲解吧。
结尾:
到这里我们的数据结构的内容就再一次的讲解完毕了,很快的我们的数据结构排序板块的内容就要结束了,后面我们还要对我们的归并排序的非递归形式进行优化。最后希望这篇博客能为大家带来一点的帮助。
相关文章:

数据结构——排序(4)
作者:几冬雪来 时间:2023年4月12日 内容:数据结构排序内容讲解 目录 前言: 1.快速排序中的递归: 2.小区间优化: 3.递归改非递归: 4.归并排序: 5.归并排序的非递归形式&…...

C++13:搜索二叉树
目录 搜索二叉树概念 模拟实现搜索二叉树 插入函数实现 插入函数实现(递归) 查找函数实现 删除函数实现 删除函数实现(递归) 中序遍历实现 拷贝构造函数实现 析构函数实现 赋值重载 我们在最开始学习二叉树的时候,…...
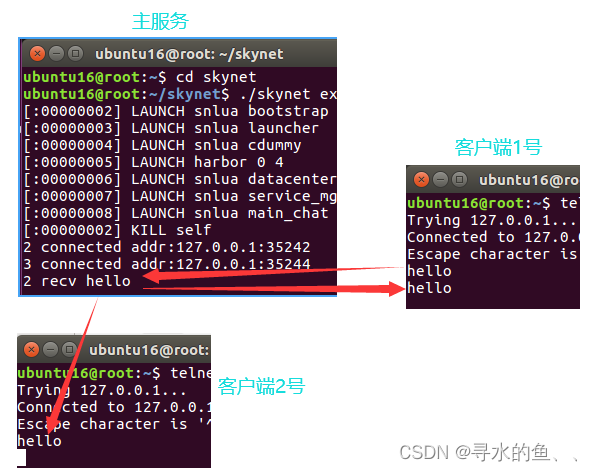
【从零开始学Skynet】基础篇(五):简易聊天室
在游戏中各玩家之间都可以进行聊天之类的交互,在这一篇中,我们就来实现一个简易的聊天室功能,这在上一篇代码的基础上很容易就能实现。1、功能需求 客户端发送一条消息,经由服务端转发,所有在线客户端都能收到…...
)
HDU - 2089 不要62(数位DP)
题目如下: 杭州人称那些傻乎乎粘嗒嗒的人为 626262(音:laoer)。 杭州交通管理局经常会扩充一些的士车牌照,新近出来一个好消息,以后上牌照,不再含有不吉利的数字了,这样一来&#x…...
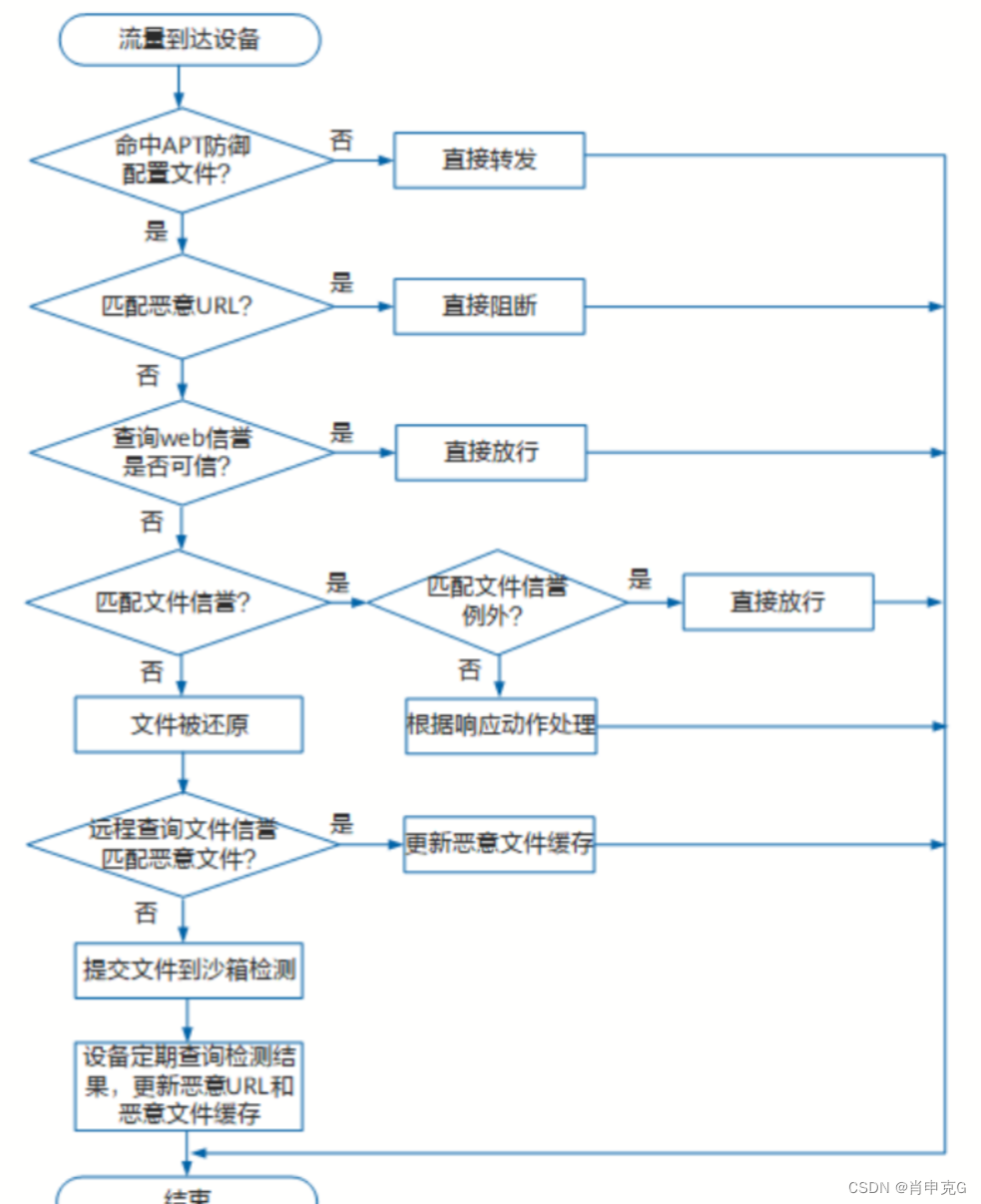
网络安全与防御
1. 什么是IDS? IDS(入侵检测系统):入侵检测是防火墙的合理补充,帮助系统对付网络攻击,扩展了系统管理员的安全管理能力,提高了信息安全基础结构的完整性。主要针对防火墙涉及不到的部分进行检测。 入侵检测主要面对的…...

【DT】蒸脱机的结构和工作原理
DT蒸脱机的结构和工作原理什么是DTDT结构图工作过程什么是DT DT 蒸脱机(DesolventazationerToaster),根据英文名可以看出来,他的作用是脱溶、烘烤。用于蒸脱湿豆粕中的溶剂。 大豆油生产工艺有2种:压榨油的加工工艺是…...

Docker管理软件
下面是一些常见的Docker管理软件 Portainer Portainer是一个轻量级的Docker管理界面,可以以用户友好的方式显示Docker环境的状态。它提供了仪表板、容器、镜像、卷、网络等功能。 Rancher Rancher是一个开源的Docker容器管理平台,支持多个主机和集群…...
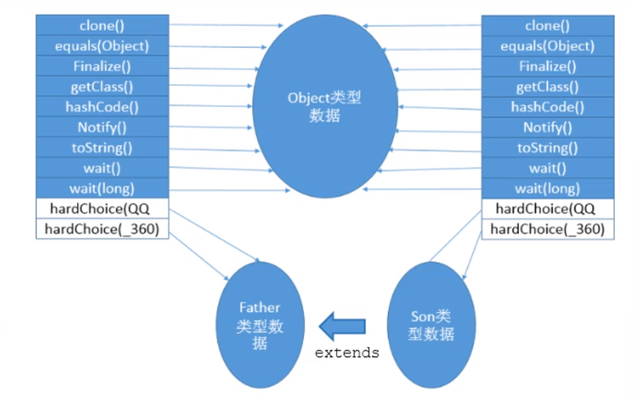
关于运行时内存数据区的一些扩展概念
栈顶缓存技术(Top-of-Stack Cashing) 前面提过,基于栈式架构的虚拟机所使用的零地址指令更加紧凑,但完成一项操作的时候必然需要使用更多的入栈和出栈指令,这同时也就意味着将需要更多的指令分派(instruction dispatc…...
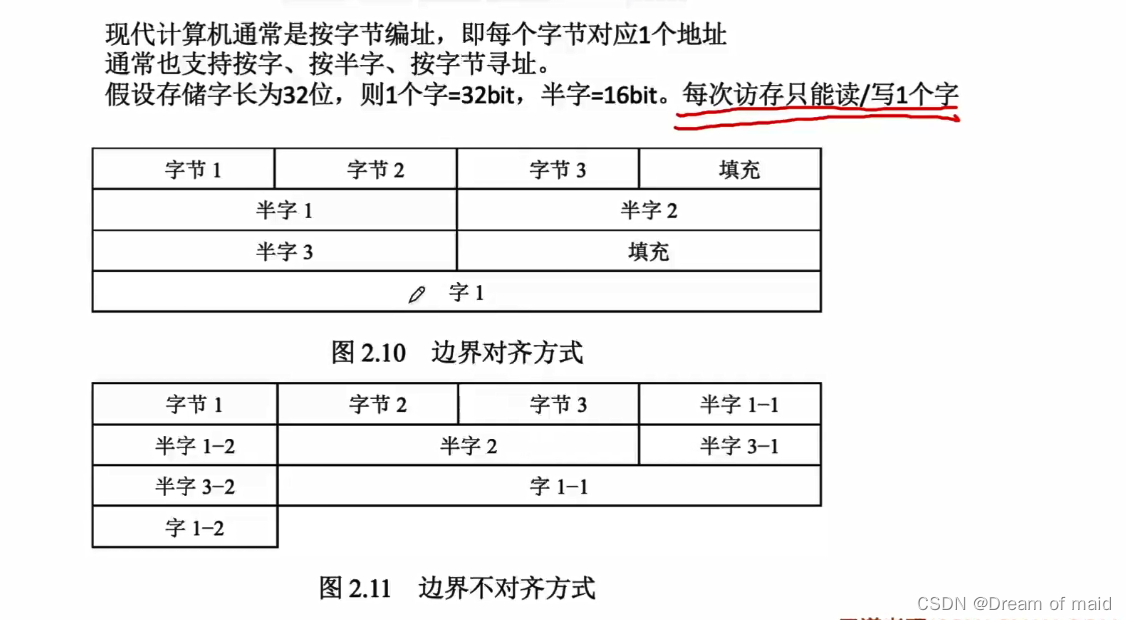
计算机组成原理第二章数据的表示与运算(中)
提示:且行且忘且随风,且行且看且从容 文章目录前言2.2.0 奇偶校验码(大纲已删)2.2.1 电路的基本原理 加法器设计2.2.2 并行进位加法器2.2.3 补码加减运算器2.2.4 标志位的生成2.2.5 定点数的移位运算2.2.62.2.6.1 原码的乘法运算2.2.6.2 补码的乘法运算2…...

我的第一台电脑的故事
第一台电脑啊,多么遥远的故事了,又似乎就在眼前。今天重回往事,就简单记录一下吧。 🌱缘起 那是初一,至今已13年,遂觉遥远,而又是立志我学习的起点,至今还在校园,又觉就…...

【1041. 困于环中的机器人】
来源:力扣(LeetCode) 描述: 在无限的平面上,机器人最初位于 (0, 0) 处,面朝北方。注意: 北方向 是 y 轴的正方向。南方向 是 y 轴的负方向。东方向 是 x 轴的正方向。西方向 是 x 轴的负方向。 机器人可…...

几何算法——4.交线(intersection curve)的表达与参数化、微分性质
几何算法——4.曲面求交的交线(intersection curve)的表达与参数化、微分性质1 关于曲面求交的交线表达2 交线的微分性质3 交线的参数化4 修正弦长参数化的微分性质1 关于曲面求交的交线表达 两个曲面求交,比较经典的方法是用跟踪法…...
【GPT】让你事半功倍特别好用的5个GPT工具
文章目录前言一、现在还能开通ChatGPT4.0吗?二、推荐五款与ChatGPT的相关实用工具1.一款浏览器插件:ChatGPT for Google2.一款生成图片的AI工具:midjourney3.推荐两款AI自动生成PPT:闪击PPT、mindshow4.识别PFD文件内容对话&#…...

人工智能大模型多场景应用原理解析
前言 在上篇文章《人工智能大模型之ChatGPT原理解析》中分享了一些大模型之ChatGPT的核心原理后,收到大量读者的反馈,诸如:在了解了核心原理后想进一步了解未来的发展趋势(比如生成式人工智能和元宇宙能擦出什么样的火花?),大模型…...
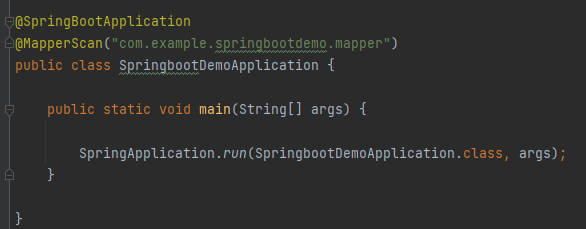
SpringBoot默认包扫描机制与默认配置文件
文章目录一、SpringBoot默认包扫描机制 - 示例二、SpringBoot默认扫描包机制 - 原理三、SpringBoot手动扫描包机制 - 原理&示例四、ComponentScan与MapperScan五、SpringBoot默认配置文件一、SpringBoot默认包扫描机制 - 示例 默认情况下,扫描启动类同级及其子…...
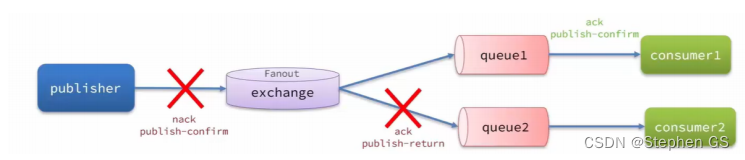
RabbitMq 消息可靠性问题(一) --- publisher发送时丢失
前言 消息从生产者发送到exchange, 再到 queue, 再到消费者。这个过程中有哪些有消息丢失的可能性呢? 发送时丢失: 生产者发送的消息未送达 exchange消息到达 exchange 后未到达 queue MQ 宕机,queue将消息丢失consumer 接收到消息后未消费…...

Java初识泛型
目录 一、包装类 1、基本数据类型和对应的包装类 2、装箱和拆箱 3、自动装箱和自动拆箱 二、什么是泛型 三、引出泛型 1、泛型的语法 四、泛型类的使用 1、语法 2、示例 3、类型推导(Type Inference) 六、泛型如何编译的 1、擦除机制 2、为什么不能实例化泛型类…...
寸照换底色技巧大全,超详细图文教程
在日常的设计工作中,我们常常需要将图片的背景色进行修改,以适应不同的场景和需求。其中最常用的方法就是寸照换底色技巧。本文将为大家介绍一些常见的寸照换底色技巧,并提供超详细的图文教程,帮助大家轻松完成这项任务。 一、使…...

这篇文章价值很大:股票历史分时成交数据怎么简单获取?【干货】
文章目录前言一、准备二、使用步骤1.引入库2,使用这个API查询历史分时数据:3.查询完整历史分时数据4.其他查询方法参数格式:[(市场代码, 股票代码), ...]参数:市场代码, 股票代码, 文件名, 起始位置, 数量参数:市场代码…...
muduo源码剖析--Buffer
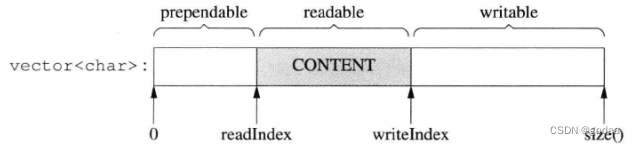
Buffer类 Buffer类是自定义处理数据输入缓冲的类,底层是vector< char >,通过readIdx和writeIdx将缓冲区分为3个部分,第一部分是预留的8字节已经读出的缓冲区字节数、第二部分是还未读出的部分、第三部分是可写的部分。 Buffer类的设计…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
