【离散数学】图论
1、有n个点没有边 零图
2、有1个点没有边 平凡图
3、含有平行边的图 多重图
4、简单图 不含有平行边和自回环的图
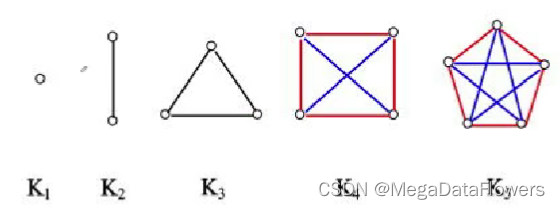
5、任意两个结点之间都有边 完全图
6、环贡献 两度
7、所有顶点的度数之和等于边数的两倍
8、在有向图中所有顶点的出度之和 或者 入度之和 等于边数
9、度数为奇数称为奇结点
10、度数为偶数称为偶结点
11、奇结点的个数为偶数
12、无向完全图
1 每个顶点的度数为n-1
2 无向完全图有n(n-1)/2条边
13、子图：点集与边集都是子集
14、生成子图：点集相等边集是子集
15、简单路：边互不相同的路
16、初级路：点互不相同的路
注意：
相关文章：
【离散数学】图论
1、有n个点没有边 零图 2、有1个点没有边 平凡图 3、含有平行边的图 多重图 4、简单图 不含有平行边和自回环的图 5、任意两个结点之间都有边 完全图 6、环贡献 两度 7、所有顶点的度数之和等于边数的两倍 8、在有向图中所有顶点的出度之和 或者 入度之和 等于边数 9、度数为…...
代码随想录算法训练营第三十七天-贪心算法6｜ 738.单调递增的数字 968.监控二叉树 总结
738.单调递增的数字 贪心算法 题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。 例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]--&#…...
【Linux】线程中的互斥锁、条件变量、信号量（数据安全问题、生产消费模型、阻塞队列和环形队列的实现）
文章目录1、线程互斥1.1 线程间频繁切换导致的问题1.2 使用互斥锁1.3 互斥锁的原理1.4 线程中的数据安全问题2、线程同步之条件变量2.1 生产消费模型2.2 条件变量概念和调用函数2.3 阻塞队列的实现3、线程同步之信号量3.1 理解信号量3.2 信号量接口3.3 环形队列的实现4、小结1、…...
MySQL8.0的安装和配置
🎉🎉🎉点进来你就是我的人了 博主主页：🙈🙈🙈戳一戳,欢迎大佬指点!人生格言：当你的才华撑不起你的野心的时候,你就应该静下心来学习! 欢迎志同道合的朋友一起加油喔🦾&am…...
LinuxGUI自动化测试框架搭建（三）-虚拟机安装（Hyper-V或者VMWare）
（三）-虚拟机安装（Hyper-V或者VMWare）1 Hyper-V安装1.1 方法一：直接启用1.2 方法二：下载安装1.3 打开Hyper-V2 VMWare安装注意：Hyper-V或者VMWare只安装一个，只安装一个，只…...
，包含copypaste、翻转、cutout等八种增强方式)
改进YOLO系列：数据增强扩充(有增强图像和标注)，包含copypaste、翻转、cutout等八种增强方式
这里写目录标题 一、简介二、数据增强方法介绍复制-粘贴（Copy-paste）翻转（Flip）Cutout加噪声（Noise）亮度调整（Brightness）平移（Shift）旋转（Rotation）裁剪（Crop）copy-paste的代码一、简介 数据增强是一种通过对原始数据进行随机变换、扰动等操作来生成新的训练样…...
c++11 标准模板（STL）（std::stack）（一）
定义于头文件 <stack> template< class T, class Container std::deque<T> > class stack;std::stack 类是容器适配器，它给予程序员栈的功能——特别是 FILO （先进后出）数据结构。 该类模板表现为底层容器的包装…...
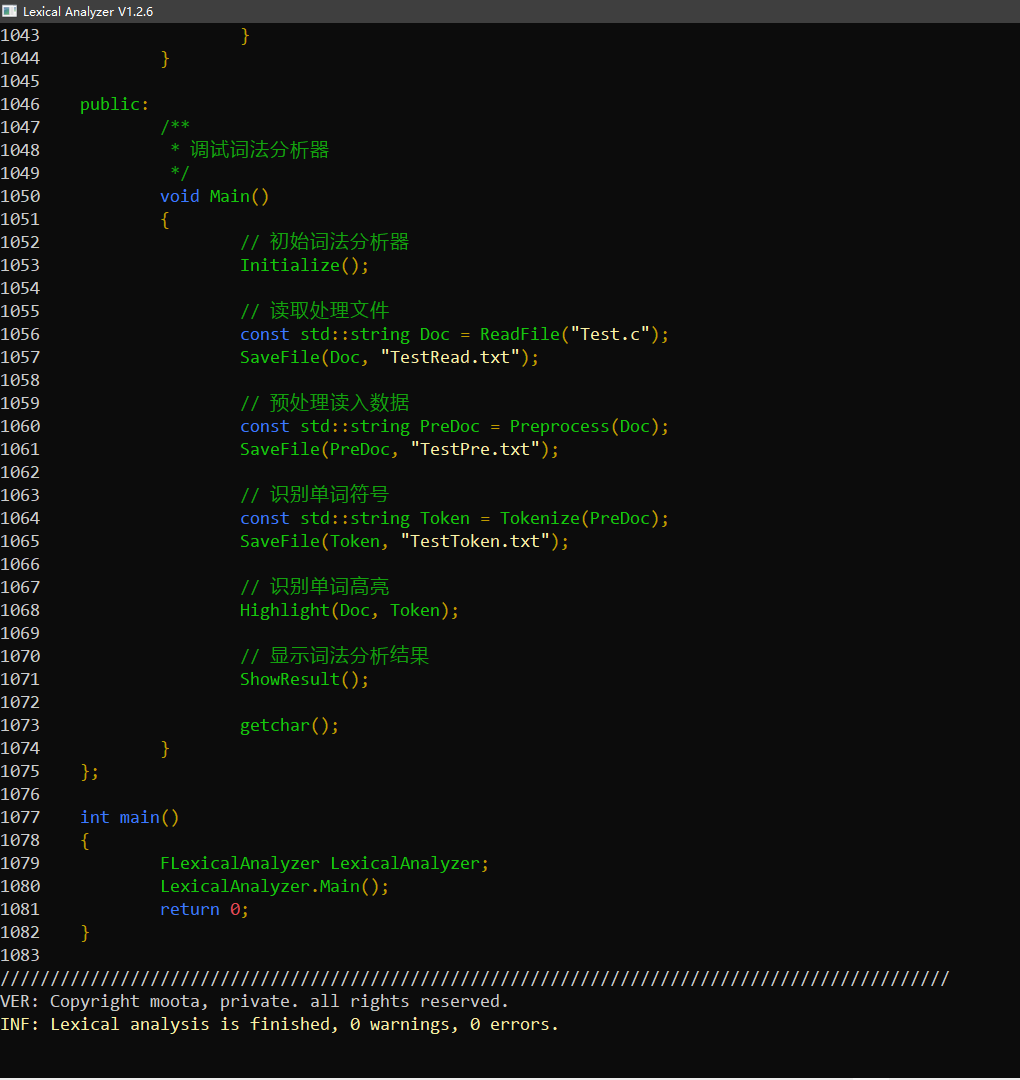
C++-c语言词法分析器
一、运行截图 对于 Test.c 的词法分析结果 对于词法分析器本身的源代码的分析结果 二、主要功能 经过不断的修正和测试代码，分析测试结果，该词法分析器主要实现了以下功能： 1. 识别关键字 实验要求：if else while do for main…...
Maven工具复习
Maven从入门到放弃Maven概述Maven 的配置Maven的基本使用IDEA 配置MAVENMaven坐标IDEA 创建MavenIDEA 导入Maven关于右侧Maven小标签(也就是Maven面板)找不到问题的解决办法关于不小心把IDEA主菜单搞消失的解决办法依赖管理Maven概述 Maven是一个工具提供了一套标准的项目结构…...
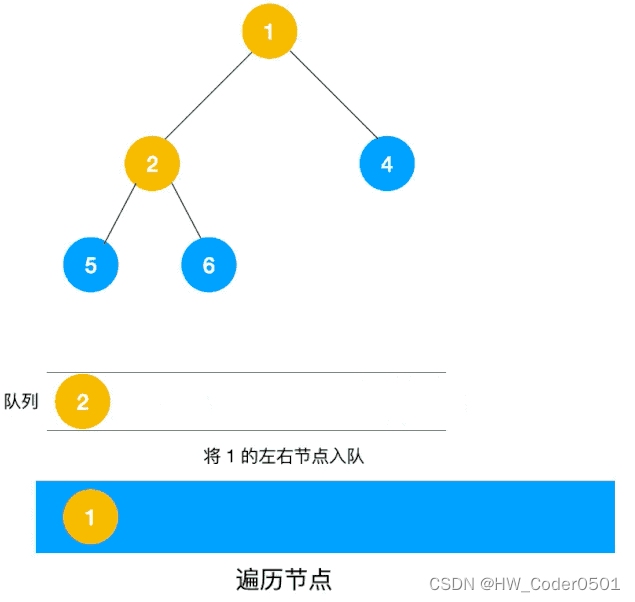
算法总结-深度优先遍历和广度优先遍历
深度优先遍历(Depth First Search，简称DFS) 与广度优先遍历(Breath First Search，简称BFS)是图论中两种非常重要的算法，生产上广泛用于拓扑排序，寻路(走迷宫)，搜索引擎，爬虫等。 一、深度优先遍历 深度优先…...
【Linux】Centos安装mvn命令（maven）
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区：运维交流社区 欢迎大家的加入！ 文章目录一、下载maven包方法一：官…...
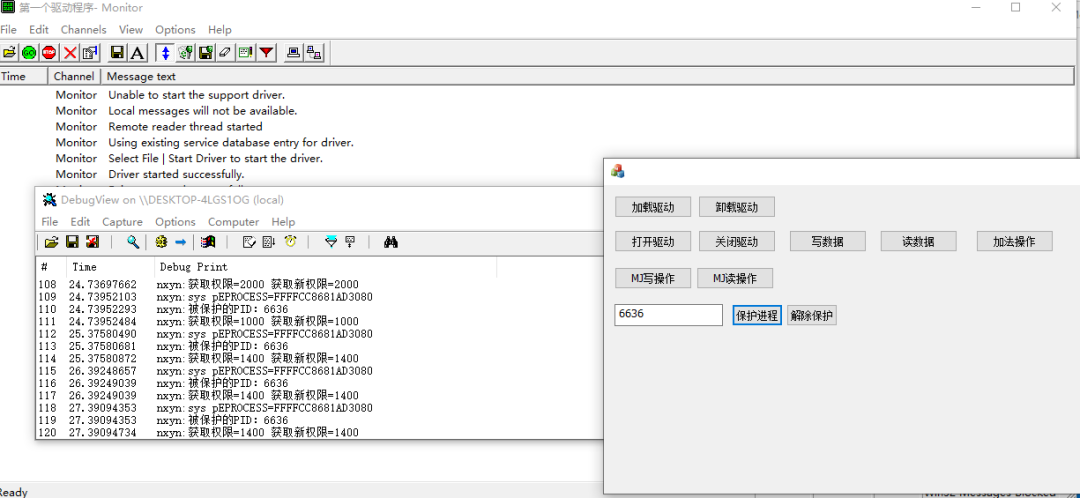
驱动保护 -- 通过PID保护指定进程
一、设计界面 1、添加一个编辑框输入要保护的进程PID，并添加两个按钮，一个保护进程，一个解除保护 2、右击编辑框，添加变量 二、驱动层代码实现 1、声明一个受保护的进程PID数组 static UINT32 受保护的进程PID[256] { 0 }; 2…...
spring常用注解（全）
一、前言 Spring的一个核心功能是IOC，就是将Bean初始化加载到容器中，Bean是如何加载到容器的，可以使用Spring注解方式或者Spring XML配置方式。 Spring注解方式减少了配置文件内容，更加便于管理，并且使用注解可以大大…...
Axios请求（对于ajax的二次封装）——Axios请求的响应结构、默认配置
Axios请求（对于ajax的二次封装）——Axios请求的响应结构、默认配置知识回调（不懂就看这儿！）场景复现核心干货axios请求的响应结构响应格式详解实际请求中的响应格式axios请求的默认配置全局axios默认值（了解…...
（三）【软件设计师】计算机系统—CPU习题联系
文章目录一、2014年上半年第1题二、2014年下半年第3题三、2017年上半年第1题四、2009年下半年第1题五、2010年上半年第5题六、2011年下半年第5题七、2011年下半年第6题八、2012年下半年第1题九、2019年上半年第1题十、2010年上半年第1题十一、2011年上半年第1题十二、2016年下半…...
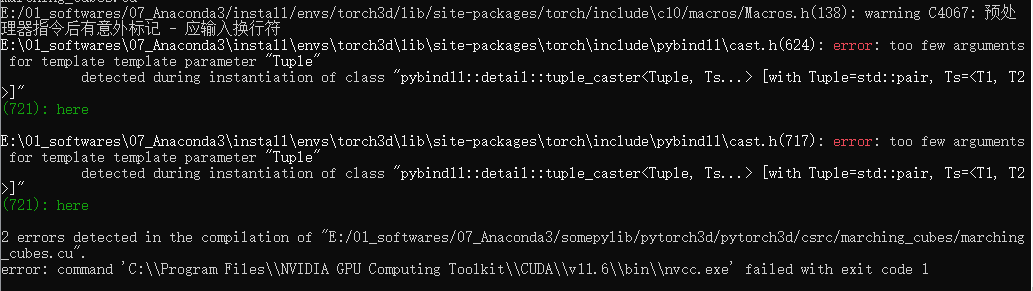
win下配置pytorch3d
一、配置好的环境：py 3.9 pytorch 1.8.0 cuda 11.1_cudnn 8_0 pytorch3d 0.6.0 CUB 1.11.0 你可能觉得pytorch3d 0.6.0版本有点低，但是折腾不如先配上用了，以后有需要再说。 （后话：py 3.9 pytorch 1.12.1 cuda …...
JS字符串对象
、 JS字符串对象 1.1 内置对象简介 在 JavaScript 中，对象是非常重要的知识点。对象可以分为两种:一种是“自定义对象”外一种是“内置对象”。自定义对象，指的是需要我们自己定义的对象，和“自定义函数”是一些道理;内置对象，…...
Linux系统对文件及目录的权限管理（chmod、chown）
1、身份介绍 在linux系统中，对文件或目录来说访问者的身份有三种： ①、属主用户，拥有者（owner）文件的创建者 ②、属组用户，和文件的owner同组的用户（group）； ③、其他用…...
半透明反向代理 (基于策略路由)
定义 半透明反向代理一般是指 代理本身对于客户端透明，对于服务端可见。 从客户端视角看，客户端访问的还是服务端，客户端不知道代理的存在。 从服务端视角看，服务端只能看到代理，看不到真实的客户端。 示意图 客户端…...
课前测5-超级密码
目录 课前测5-超级密码 程序设计 程序分析 课前测5-超级密码 【问题描述】 上次设计的“高级密码”被你们破解了，一丁小朋友很不服气！ 现在，他又设计了一套更加复杂的密码，称之为“超级密码”。 说实话，这套所谓的“超级密码”其实也并不难： 对于一个给定的字符…...
ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上，你可以使用apt包管理器来安装NFS服务器。打开终端并运行： sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享，例如/shared： sudo mkdir /shared sud…...
Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接：3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯，要想要能够将所有的电脑解锁&#x…...
深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式（Singleton Pattern&#…...
Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
是否存在路径（FIFOBB算法）
题目描述 一个具有 n 个顶点e条边的无向图，该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序，确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数，分别表示n 和 e 的值（1…...
Linux --进程控制
本文从以下五个方面来初步认识进程控制： 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程，创建出来的进程就是子进程，原来的进程为父进程。…...
服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行！ sudo su - 1. CentOS 系统： yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体（对象或容器）QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质（定义颜色、反光等）QFirstPersonC…...
【JVM】Java虚拟机（二）——垃圾回收
目录 一、如何判断对象可以回收 （一）引用计数法 （二）可达性分析算法 二、垃圾回收算法 （一）标记清除 （二）标记整理 （三）复制 （四ÿ…...
day36-多路IO复用
一、基本概念 （服务器多客户端模型） 定义：单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用：应用程序通常需要处理来自多条事件流中的事件，比如我现在用的电脑，需要同时处理键盘鼠标…...