当前位置： 首页 > news >正文

改进YOLO系列：数据增强扩充(有增强图像和标注)，包含copypaste、翻转、cutout等八种增强方式

news 2026/2/9 0:29:22

这里写目录标题

  • 一、简介
  • 二、数据增强方法介绍
    • 复制-粘贴（Copy-paste）
    • 翻转（Flip）
    • Cutout
    • 加噪声（Noise）
    • 亮度调整（Brightness）
    • 平移（Shift）
    • 旋转（Rotation）
    • 裁剪（Crop）
  • copy-paste的代码

一、简介

数据增强是一种通过对原始数据进行随机变换、扰动等操作来生成新的训练样本的技术，可以有效提高深度学习模型的泛化性能。在目标检测任务中，数据增强的作用尤为重要，因为目标检测涉及到对图像中目标位置、大小、姿态等多个因素的精确识别，需要对模型进行充分的训练以适应各种复杂情况。下面对常见的目标检测数据增强方法进行介绍。

二、数据增强方法介绍

复制-粘贴（Copy-paste）

Copy-p

相关文章：

改进YOLO系列：数据增强扩充(有增强图像和标注)，包含copypaste、翻转、cutout等八种增强方式

这里写目录标题 一、简介二、数据增强方法介绍复制-粘贴（Copy-paste）翻转（Flip）Cutout加噪声（Noise）亮度调整（Brightness）平移（Shift）旋转（Rotation）裁剪（Crop）copy-paste的代码一、简介 数据增强是一种通过对原始数据进行随机变换、扰动等操作来生成新的训练样…...

编程日记 2023/4/16 3:09:14

c++11 标准模板（STL）（std::stack）（一）

定义于头文件 <stack> template< class T, class Container std::deque<T> > class stack;std::stack 类是容器适配器&#xff0c;它给予程序员栈的功能——特别是 FILO &#xff08;先进后出&#xff09;数据结构。 该类模板表现为底层容器的包装…...

编程日记 2023/4/16 3:04:13

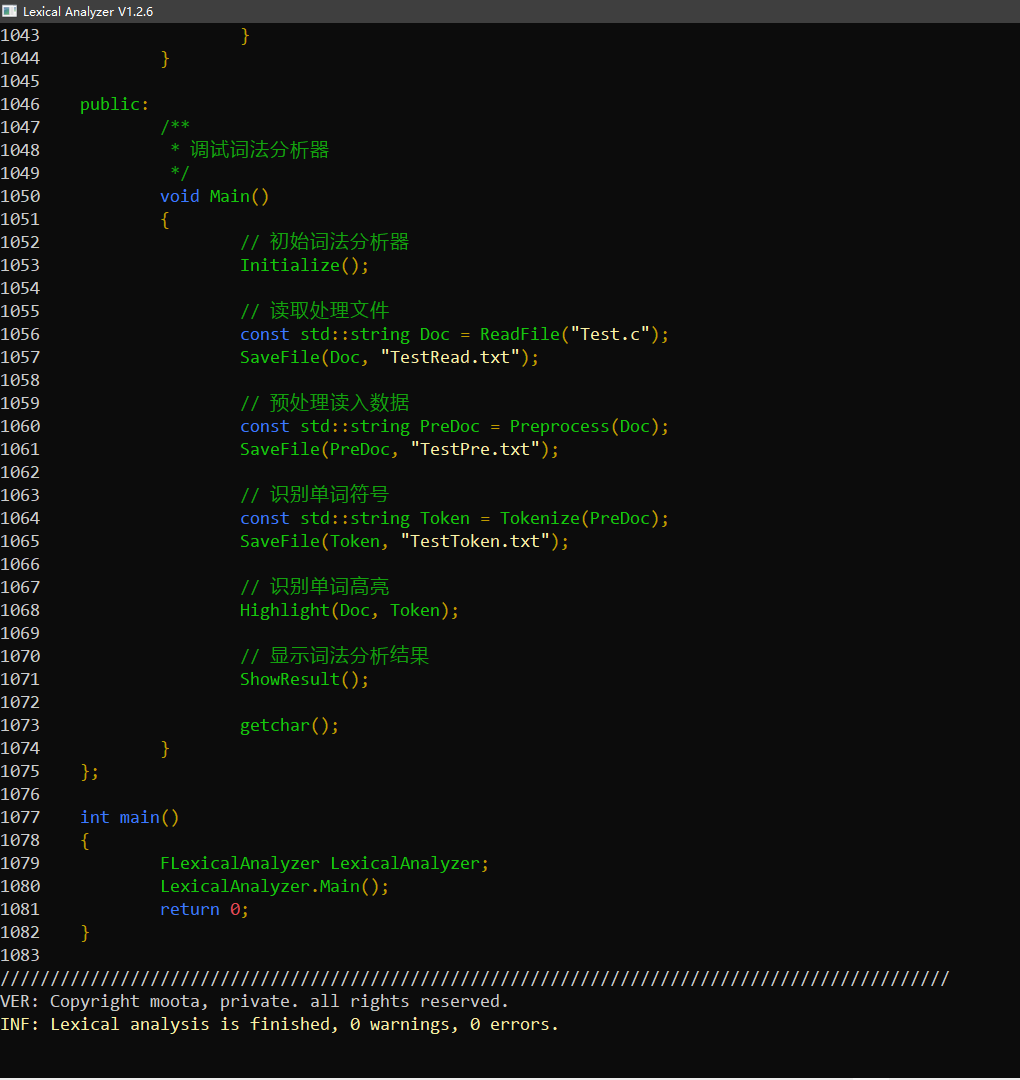
C++-c语言词法分析器

一、运行截图 对于 Test.c 的词法分析结果 对于词法分析器本身的源代码的分析结果 二、主要功能 经过不断的修正和测试代码&#xff0c;分析测试结果&#xff0c;该词法分析器主要实现了以下功能&#xff1a; 1. 识别关键字 实验要求&#xff1a;if else while do for main…...

编程日记 2023/4/16 2:59:12

Maven工具复习

Maven从入门到放弃Maven概述Maven 的配置Maven的基本使用IDEA 配置MAVENMaven坐标IDEA 创建MavenIDEA 导入Maven关于右侧Maven小标签(也就是Maven面板)找不到问题的解决办法关于不小心把IDEA主菜单搞消失的解决办法依赖管理Maven概述 Maven是一个工具提供了一套标准的项目结构…...

编程日记 2023/4/16 2:54:11

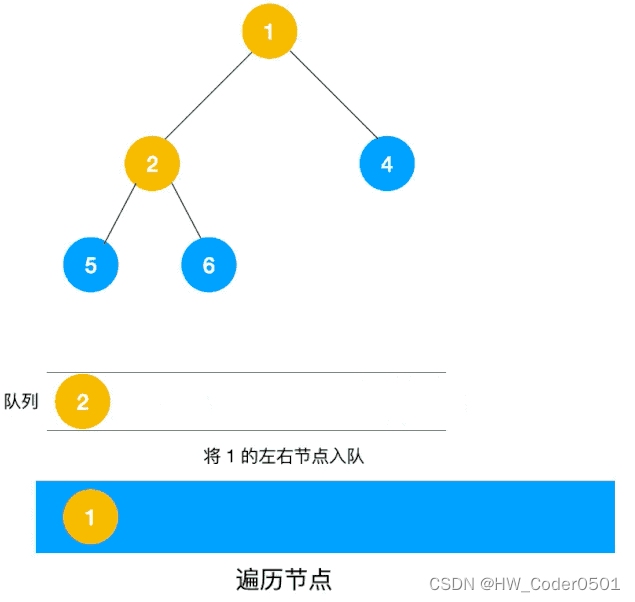
算法总结-深度优先遍历和广度优先遍历

深度优先遍历(Depth First Search&#xff0c;简称DFS) 与广度优先遍历(Breath First Search&#xff0c;简称BFS)是图论中两种非常重要的算法&#xff0c;生产上广泛用于拓扑排序&#xff0c;寻路(走迷宫)&#xff0c;搜索引擎&#xff0c;爬虫等。 一、深度优先遍历 深度优先…...

编程日记 2023/6/1 13:05:58

【Linux】Centos安装mvn命令（maven）

&#x1f341;博主简介 &#x1f3c5;云计算领域优质创作者   &#x1f3c5;华为云开发者社区专家博主   &#x1f3c5;阿里云开发者社区专家博主 &#x1f48a;交流社区&#xff1a;运维交流社区 欢迎大家的加入&#xff01; 文章目录一、下载maven包方法一&#xff1a;官…...

编程日记 2023/4/16 2:44:09

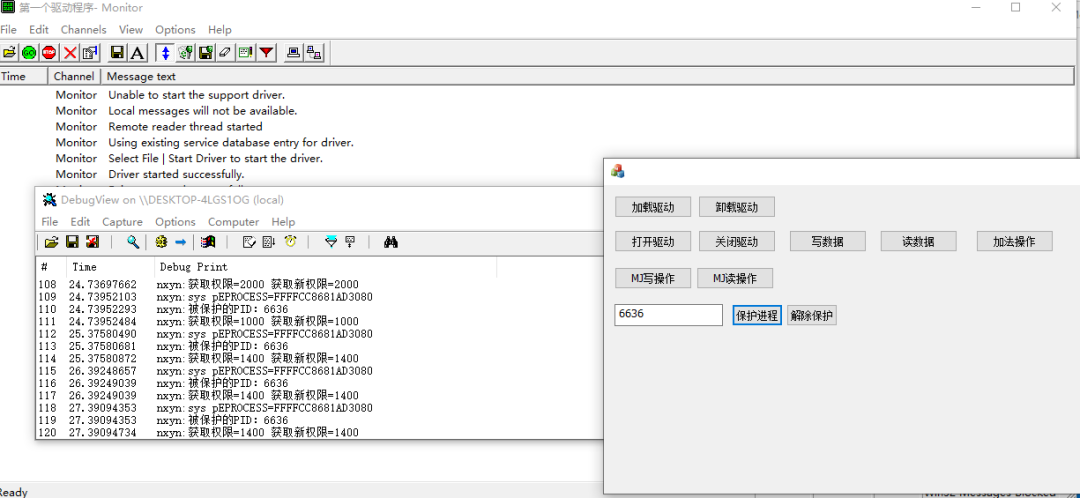
驱动保护 -- 通过PID保护指定进程

一、设计界面 1、添加一个编辑框输入要保护的进程PID&#xff0c;并添加两个按钮&#xff0c;一个保护进程&#xff0c;一个解除保护 2、右击编辑框&#xff0c;添加变量 二、驱动层代码实现 1、声明一个受保护的进程PID数组 static UINT32 受保护的进程PID[256] { 0 }; 2…...

编程日记 2023/4/16 2:39:07

spring常用注解（全）

一、前言 Spring的一个核心功能是IOC&#xff0c;就是将Bean初始化加载到容器中&#xff0c;Bean是如何加载到容器的&#xff0c;可以使用Spring注解方式或者Spring XML配置方式。 Spring注解方式减少了配置文件内容&#xff0c;更加便于管理&#xff0c;并且使用注解可以大大…...

编程日记 2023/4/16 2:34:06

Axios请求（对于ajax的二次封装）——Axios请求的响应结构、默认配置

Axios请求&#xff08;对于ajax的二次封装&#xff09;——Axios请求的响应结构、默认配置知识回调&#xff08;不懂就看这儿&#xff01;&#xff09;场景复现核心干货axios请求的响应结构响应格式详解实际请求中的响应格式axios请求的默认配置全局axios默认值&#xff08;了解…...

编程日记 2023/4/16 2:29:05

（三）【软件设计师】计算机系统—CPU习题联系

文章目录一、2014年上半年第1题二、2014年下半年第3题三、2017年上半年第1题四、2009年下半年第1题五、2010年上半年第5题六、2011年下半年第5题七、2011年下半年第6题八、2012年下半年第1题九、2019年上半年第1题十、2010年上半年第1题十一、2011年上半年第1题十二、2016年下半…...

编程日记 2023/4/16 2:24:04

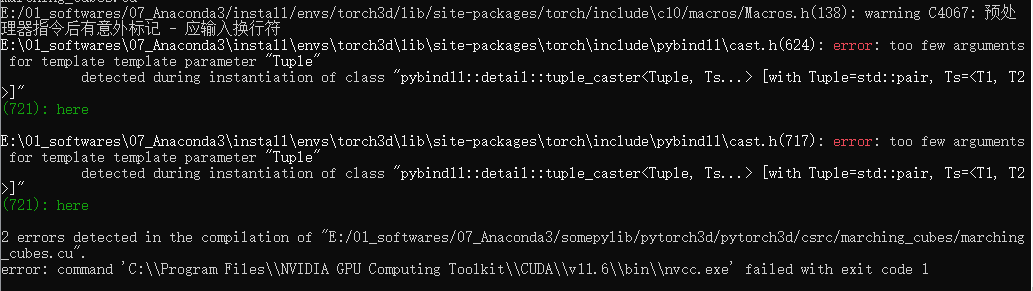
win下配置pytorch3d

一、配置好的环境&#xff1a;py 3.9 pytorch 1.8.0 cuda 11.1_cudnn 8_0 pytorch3d 0.6.0 CUB 1.11.0 你可能觉得pytorch3d 0.6.0版本有点低&#xff0c;但是折腾不如先配上用了&#xff0c;以后有需要再说。 &#xff08;后话&#xff1a;py 3.9 pytorch 1.12.1 cuda …...

编程日记 2023/4/16 2:19:03

JS字符串对象

、 JS字符串对象 1.1 内置对象简介 在 JavaScript 中&#xff0c;对象是非常重要的知识点。对象可以分为两种:一种是“自定义对象”外一种是“内置对象”。自定义对象&#xff0c;指的是需要我们自己定义的对象&#xff0c;和“自定义函数”是一些道理;内置对象&#xff0c;…...

编程日记 2023/4/16 2:14:02

Linux系统对文件及目录的权限管理（chmod、chown）

1、身份介绍 在linux系统中&#xff0c;对文件或目录来说访问者的身份有三种&#xff1a; ①、属主用户&#xff0c;拥有者&#xff08;owner&#xff09;文件的创建者 ②、属组用户&#xff0c;和文件的owner同组的用户&#xff08;group&#xff09;&#xff1b; ③、其他用…...

编程日记 2023/5/31 21:20:25

半透明反向代理 (基于策略路由)

定义 半透明反向代理一般是指 代理本身对于客户端透明&#xff0c;对于服务端可见。 从客户端视角看&#xff0c;客户端访问的还是服务端&#xff0c;客户端不知道代理的存在。 从服务端视角看&#xff0c;服务端只能看到代理&#xff0c;看不到真实的客户端。 示意图 客户端…...

编程日记 2023/4/16 2:04:00

课前测5-超级密码

目录 课前测5-超级密码 程序设计 程序分析 课前测5-超级密码 【问题描述】 上次设计的“高级密码”被你们破解了，一丁小朋友很不服气！ 现在，他又设计了一套更加复杂的密码，称之为“超级密码”。 说实话，这套所谓的“超级密码”其实也并不难： 对于一个给定的字符…...

编程日记 2023/4/16 1:58:59

QML控件--Menu

文章目录一、控件基本信息二、控件使用三、属性成员四、成员函数一、控件基本信息 二、控件使用 import QtQuick 2.10 import QtQuick.Window 2.10 import QtQuick.Controls 2.3ApplicationWindow{visible: true;width: 1280;height: 720;Button {id: fileButtontext: "Fi…...

编程日记 2023/4/16 1:53:58

002：Mapbox GL更改大气、空间及星星状态

第002个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中更改大气、空间及星星状态 。 直接复制下面的 vue+mapbox源代码，操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码（共71行）相关API参考：专栏目标示例效果 配置方式 1）查看基础设置：…...

编程日记 2023/4/16 1:48:56

2022年第十三届蓝桥杯题解（全）C/C++

A题就是一个简单的进制转化&#xff0c;代码实现如下&#xff1a; #include <bits/stdc.h>using namespace std;const int N 1e5 10;int main() {int x 2022;int a 1;int res 0;while(x) {res (x % 10) * a;a a * 9;x / 10;}cout << res;return 0; } B题有…...

编程日记 2023/4/16 1:43:55

【cmake学习】find_package 详解

find_package 主要用于查找指定的 package&#xff0c;主要支持两种搜索方法&#xff1a; Config mode&#xff1a;查找 xxx-config.cmake或 xxxConfig.cmake的文件&#xff0c;如OpenCV库的OpenCVConfig.cmakeModule mode&#xff1a;查找Findxxx.cmake文件&#xff0c;如Ope…...

编程日记 2023/4/16 1:38:53

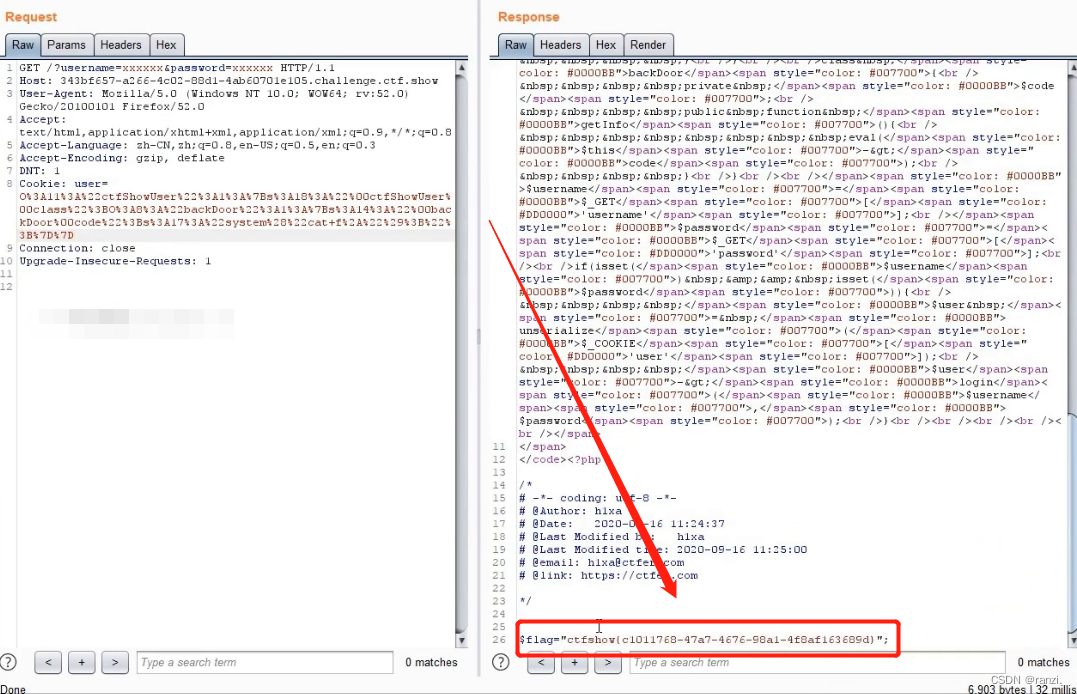
WEB攻防-通用漏洞PHP反序列化POP链构造魔术方法原生类

目录 一、序列化和反序列化 二、为什么会出现反序列化漏洞 三、序列化和反序列化演示 <演示一> <演示二> <演示二> 四、漏洞出现演示 <演示一> <演示二> 四、ctfshow靶场真题实操 <真题一> <真题二> <真题三> &l…...

编程日记 2023/5/31 14:18:41

云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？

大家好&#xff0c;欢迎来到《云原生核心技术》系列的第七篇&#xff01; 在上一篇&#xff0c;我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在&#xff0c;我们就像一个拥有了一块崭新数字土地的农场主&#xff0c;是时…...

编程新知 2025/12/14 22:32:59

DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径

目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

编程新知 2025/11/20 2:48:44

工业安全零事故的智能守护者：一体化AI智能安防平台

前言&#xff1a; 通过AI视觉技术&#xff0c;为船厂提供全面的安全监控解决方案&#xff0c;涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面&#xff0c;能够实现对应负责人反馈机制&#xff0c;并最终实现数据的统计报表。提升船厂…...

编程新知 2026/1/21 9:20:07

边缘计算医疗风险自查APP开发方案

核心目标：在便携设备（智能手表/家用检测仪）部署轻量化疾病预测模型，实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

编程新知 2026/1/28 10:02:54

【Linux】C语言执行shell指令

在C语言中执行Shell指令 在C语言中&#xff0c;有几种方法可以执行Shell指令&#xff1a; 1. 使用system()函数 这是最简单的方法&#xff0c;包含在stdlib.h头文件中&#xff1a; #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

编程新知 2025/11/20 18:42:48

深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法

深入浅出&#xff1a;JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中&#xff0c;随机数的生成看似简单&#xff0c;却隐藏着许多玄机。无论是生成密码、加密密钥&#xff0c;还是创建安全令牌&#xff0c;随机数的质量直接关系到系统的安全性。Jav…...

编程新知 2025/10/8 4:56:09

鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/

使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题&#xff1a;docker pull 失败 网络不同&#xff0c;需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

编程新知 2025/12/31 6:28:08

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的？

uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件&#xff0c;用于在原生应用中加载 HTML 页面&#xff1a; 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

编程新知 2025/8/6 2:19:46

中医有效性探讨

文章目录 西医是如何发展到以生物化学为药理基础的现代医学&#xff1f;传统医学奠基期&#xff08;远古 - 17 世纪&#xff09;近代医学转型期&#xff08;17 世纪 - 19 世纪末&#xff09;​现代医学成熟期&#xff08;20世纪至今&#xff09; 中医的源远流长和一脉相承远古至…...

编程新知 2026/1/23 7:56:54

七、数据库的完整性

七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

编程新知 2026/2/4 10:28:25