动态规划之01背包问题和完全背包问题
01背包的问题描述:(内容参考代码随想录)
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
问题示例:
背包最大重量为4。
重量 | 价值 | |
物品0 | 1 | 15 |
物品1 | 3 | 20 |
物品2 | 4 | 30 |
解法一:暴力求解
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是o(2^n),这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
解法二:二维dp数组01背包
1.确定dp数组以及下标的含义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2.确定递推公式
不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3.dp数组初始化
如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。

从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
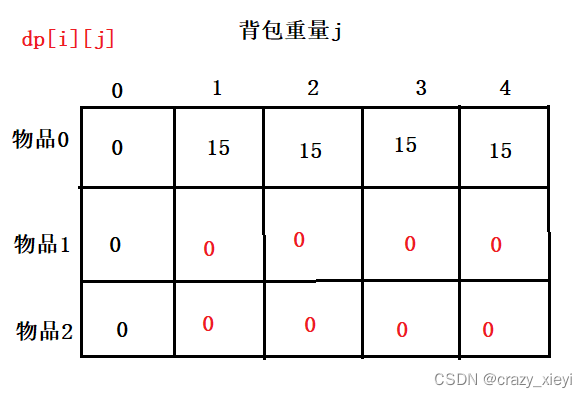
4.确定遍历顺序
虽然两个for循环遍历的次序不同,不管是先遍历背包还是先遍历物品,dp[i][j]所需要的数据就是左上角,根本是不影响结果的。
public static void main(String[] args) {int[] weight = {1,3,4};int[] value = {15,20,30};int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){// 创建dp数组int goods = weight.length; // 获取物品的数量int[][] dp = new int[goods][bagSize + 1];// 初始化dp数组// 创建数组后,其中默认的值就是0for (int j = weight[0]; j <= bagSize; j++) {dp[0][j] = value[0];}// 填充dp数组for (int i = 1; i < weight.length; i++) {for (int j = 1; j <= bagSize; j++) {if (j < weight[i]) {/*** 当前背包的容量都没有当前物品i大的时候,是不放物品i的* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值*/dp[i][j] = dp[i-1][j];} else {/*** 当前背包的容量可以放下物品i* 那么此时分两种情况:* 1、不放物品i* 2、放物品i* 比较这两种情况下,哪种背包中物品的最大价值最大*/dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);}}}// 打印dp数组for (int i = 0; i < goods; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println("\n");}}解法三:一维dp数组01背包
1.确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2.一维dp数组的递推公式
dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值。
3.一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
根据递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);所以在初始化的时候不能初始化较大的值,因为dp[j]是求最大值得出的,不然会影响结果,初始为非负数中最小的就行,初始化为0就合适。
4.一维dp数组遍历顺序
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。倒序遍历是为了保证物品i只被放入一次!因为一维数组的结果要依赖前一次的结果,所以如果正序遍历,那么就会造成前面的结果重复计算。所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
为什么二维dp数组历的时候不用倒序呢?因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
两个嵌套for循环的顺序,一定是先遍历物品嵌套遍历背包容量,不能颠倒。
public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWight = 4;testWeightBagProblem(weight, value, bagWight);}public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){int wLen = weight.length;//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值int[] dp = new int[bagWeight + 1];//遍历顺序:先遍历物品,再遍历背包容量for (int i = 0; i < wLen; i++){for (int j = bagWeight; j >= weight[i]; j--){dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}//打印dp数组for (int j = 0; j <= bagWeight; j++){System.out.print(dp[j] + " ");}}小结:
01背包问题,用二维数组dp[i][j]和一维数组dp[i]来求解,两者有很大区别。在dp数组的含义,dp数组的初始化,以及for循环嵌套顺序以及遍历顺序都是不同的。
完全背包问题
01背包和完全背包的区别在于,01背包的物品只能使用一次,而完全背包的物品可以无限次使用,所以在遍历顺序上是有区别的。01背包问题为了能让每个物品只使用一次,所以是倒序遍历背包,而完全背包就改为正序遍历了。很简单的理解啊,因为正序遍历,后一个背包状态要依赖前一个背包的状态,所以一个物品可以被加了多次,而倒序遍历,因为前面的背包状态是初始值,所以后一个背包加了前面的背包状态也是无效的。同样,跟01背包的dp二维数组一样,两层for循环也是可以颠倒的。
//先遍历物品,再遍历背包
private static void testCompletePack(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 0; i < weight.length; i++){ // 遍历物品for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量for (int j = 0; j < weight.length; j++){ // 遍历物品if (i - weight[j] >= 0){dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);}}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}相关文章:

动态规划之01背包问题和完全背包问题
01背包的问题描述:(内容参考代码随想录)有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。问题示例&#…...
)
MATLAB算法实战应用案例精讲-【图像处理】数字图像灰度化(附Java、python、matlab和opencv代码实现)
目录 前言 几个相关概念 1、RGB 2、ARGB 3、灰度化 4.图像点运算 5.线性点运算...
)
Linux(强大的yum命令)
yum 读 [jʌm] ,中文谐音: 样安ing。 yum( Yellow dog Updater, Modified)是一个在 Fedora 和 RedHat 以及 SUSE 中的 Shell 前端软件包管理器。 基于 RPM 包管理,能够从指定的服务器自动下载 RPM 包并且安装&#x…...

28.结语
文章目录28 Epilogue 结语28 Epilogue 结语 Don’t let it end like this. Tell them I said something. 不要让它就这样结束。 告诉他们我说了些什么 —Pancho Villa 您已到达旅程的尽头。 辛苦了 我们希望您能从本书中找到一些有价值的收获。 我们建议该列表应包括以下内…...

ICRS、GCRS、CIRS、TIRS和ITRS坐标系统简介
ICRS、GCRS、CIRS、TIRS和ITRS坐标系统简介1. 简介2. ICRS、GCRS、CIRS、TIRS和ITRS分别介绍2.1 ICRS详细说明2.2 GCRS详细说明2.3 CIRS详细说明2.4 TIRS详细说明2.5 ITRS 详细说明1. 简介 ICRS、GCRS、CIRS、TIRS和ITRS都是天文学中使用的坐标系统: ICRS (Intern…...
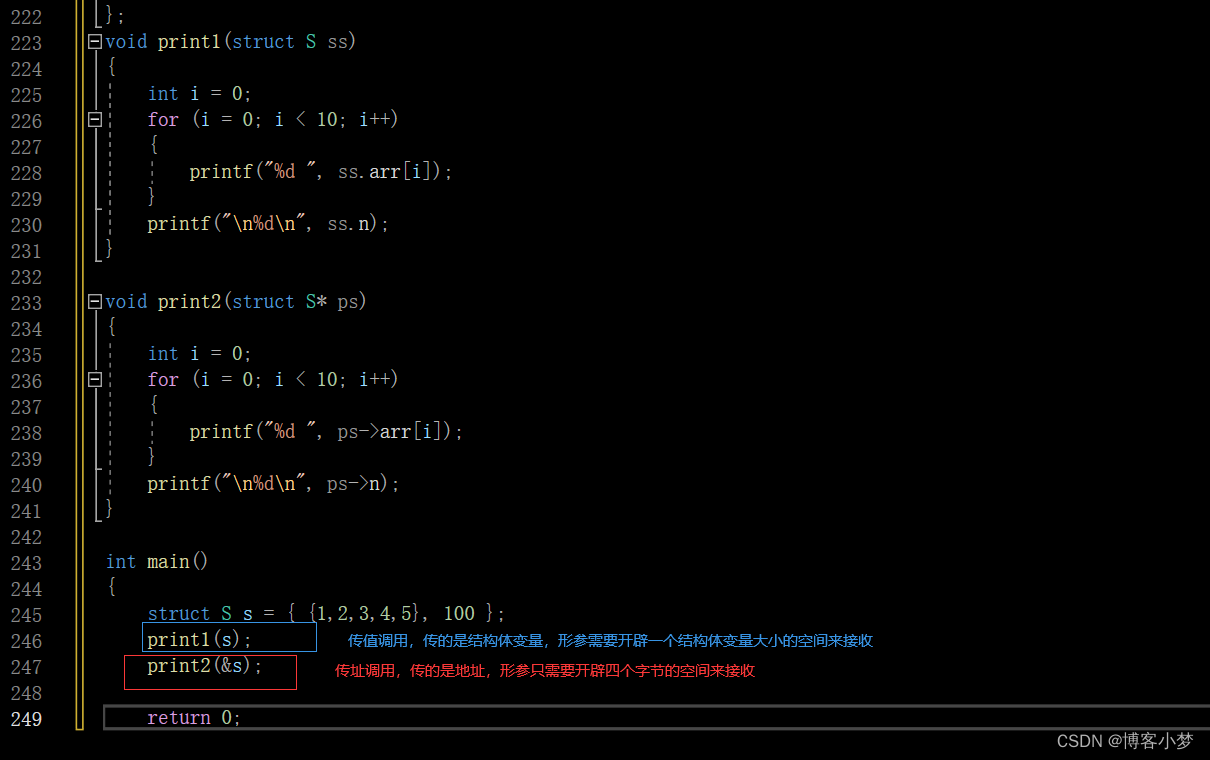
你是真的“C”——详解结构体知识点
你是真的“C”——详解结构体知识点😎前言🙌什么是结构体?🙌1. 结构体的声明🙌1.1 结构的基础知识1.2 结构的声明1.3 结构成员的类型1.4 结构体变量的定义和初始化2. 结构体成员的访问🙌3结构体传参&#x…...
 | 刷完必过)
2023新华为OD机试题 - 单词接龙(JavaScript) | 刷完必过
单词接龙 题目 单词接龙的规则是: 可用于接龙的单词,首字母必须要与前一个单词的尾字母相同; 当存在多个首字母相同的单词时,取长度最长的单词; 如果长度也相等,则取字典序最小的单词; 已经参与接龙的单词不能重复使用; 现给定一组全部由小写字母组成的单词数组, 并指…...

第一章 一般错误信息 - 错误代码 0 到 99
文章目录第一章 一般错误信息 - 错误代码 0 到 99一般错误信息错误代码 0 到 99第一章 一般错误信息 - 错误代码 0 到 99 一般错误信息 错误代码被报告为 ERROR #nnn。这些错误代码有时称为 %Status 错误代码。 可以使用 DisplayError() 和 Error() 方法确定指定错误代码的错…...
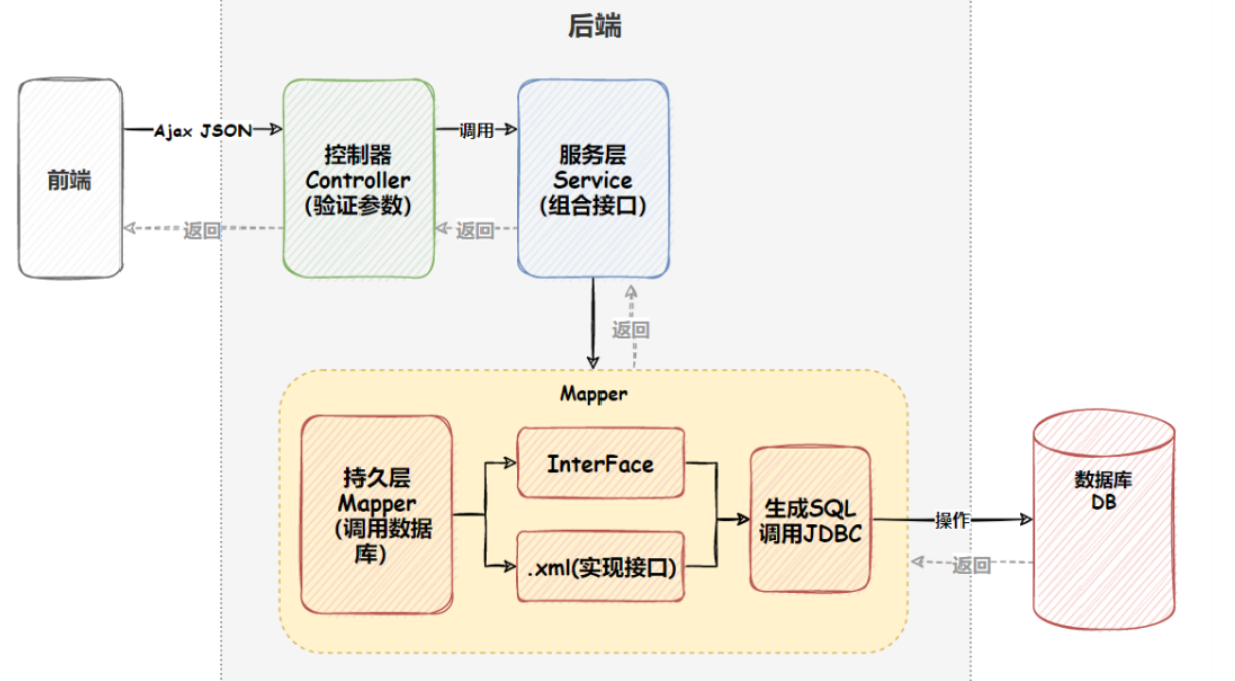
MyBatis 之一(概念、创建项目、操作模式、交互流程)
1. MyBatis 是什么MyBatis 是一款优秀的持久层框架MyBatis 也是一个 ORM (Object Relational Mapping)框架,即对象关系映射它支持自定义 SQL、存储过程以及高级映射MyBatis 去除了几乎所有的 JDBC 代码以及设置参数和获取结果集的工作MyBatis…...

学习笔记:文件
因为有的数据,数据量极大。或者是你想把编译输出的内容存储起来,就可以使用文件 读文件中内容具体操作 来自C语言详解 FILE文件操作 - 知乎 (zhihu.com) 写入文件具体操作 同样来自 C语言详解 FILE文件操作 - 知乎 (zhihu.com) 当文件关闭时,…...
)
高考结束了以后应该做的事情(个人经历的总结)
高考结束了以后应该做的事情 在本指导中,我总结了我大学期间我认为做的没有后悔,最正确的事情。同时,根据我的经历和我踩过的坑总结出来了这一份入学指南。 这个指导有点偏向于工科生,已经尽量偏向于所有专业了。对于所有专业的同…...

蓝桥杯:k倍区间
[蓝桥杯 2017 省 B] k 倍区间给定一个长度为 N 的数列,A1,A2,…AN,如果其中一段连续的子序列 Ai,Ai1,…Aj 之和是 K 的倍数,我们就称这个区间 [i,j] 是 K 倍区间。你能求出数列中总共有多少个 K 倍区间吗?输入格式第一行包含两个整…...
【思维模型】概率思维的价值:找到你的人生算法!打开你的人生格局!实现认知跃迁!
把同样公平的机会放在放在很多人面前,不同的人生算法,会得到迥然不同的结果。 概率思维是什么? 【ChatGPT】概率思维是一种通过使用数学模型来思考和评估不确定性事件的方法。它通过计算不同可能性的概率来预测事件的结果,并评估风险和机会。 概率思维的价值在于它可以帮…...

API文档自动生成工具
一、参考资料 从Python源码注释,自动生成API文档 二、问题引入 不管是开源还是闭源,要让所有人都能读懂你的代码这太难了,所以文档是很重要的。大部分情况,我们不希望维护一份代码再加上一份文档,这样做很容易造成文…...

7、MyBatis框架——MyBatis对一对一关系的处理、分步查询、MyBatis对一对多关系的处理
目录 一、项目框架搭建 二、在实体类中添加额外属性实现多表查询 1、mybatis两表关联查询 (1)实体类类型映射规则 (2)代码演示 2、分步查询 (1)autoMapping开启自动映射 (2)…...
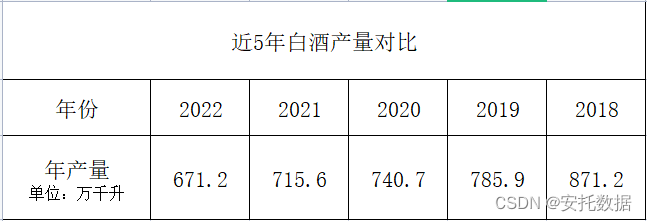
电商数据监测——中国白酒行业数据浅析
大国盛世酿,万家潭酒香。中国白酒是中国特色文化之一。 2022年,国内白酒总产量为671.2万千升,处于持续下滑的态势。 白酒产量不佳,但线上平台的销售情况却成绩优异。2022年,京东平台白酒的年度总销量超3500万件,同比去…...
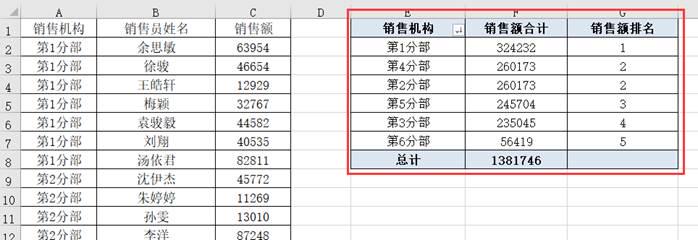
excel数据技巧:透视表快速统计年终业绩排名
年关了,各种数据多得要命,要汇总,要排名,这样才好颁奖发红包。今天,数据透视表出来为Excel人送温暖了,不用分两步做,鼠标拖两下,同步搞定业绩统计与排名。临近年末,各行各…...

TensorRT的Python接口解析
TensorRT的Python接口解析 文章目录TensorRT的Python接口解析4.1. The Build Phase4.1.1. Creating a Network Definition in Python4.1.2. Importing a Model using the ONNX Parser4.1.3. Building an Engine4.2. Deserializing a Plan4.3. Performing Inference点此链接加入…...

【信管11.5】合同、采购、招投标相关法规
合同、采购、招投标相关法规关于法律法规相关的内容,其实并没什么可以多说的,我也只是列出来,大家挑着背吧。当然,这里也不都是完完全全的法律条文,有一些也可能是一些归纳总结。更具体的内容大家可以参考教材以及查阅…...

使用 CSS 变量更改多个元素样式
使用 CSS 变量更改多个元素样式 var() 函数用于插入自定义的属性值,如果一个属性值在多处被使用,该方法就很有用。 custom-property-name 是必需的, 自定义属性的名称,必需以 – 开头。 value 可选。备用值,在属性不存在的时候使…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...
