R -- 用psych包做因子分析
因子分析
因子分析又称为EFA,是一系列用来发现一组变量的潜在结构的办法。它通过寻找一组更小的,潜在的结构来解释已观测到的显式的变量间的关系。这些虚拟的、无法观测的变量称为因子(每个因子被认为可以解释多个观测变量间共有的方差)
人话版:开豪宅,住豪车,戴名表 可以归因为 有钱(当然有钱还可以继续归因)。
开豪宅,住豪车,戴名表 这些变量是显式的,而有钱是潜在的隐式的可以解释显式变量的因子。
因子分析和主成分分析有什么区分嘛
个人觉得:因子分析和主成分分析很相似
有人说:原理不同,线性表示方向不同;假设条件不同;求解方法不同;主成分和因子的变化不同;因子数量与主成分的数量;解释重点不同;算法上的不同;优点不同;应用场景不同。
那用因子分析对“有人说的话”进行分析,可以得到潜在的因子,比如解决问题的出发点不同
主成分分析的出发点是将相关变量 打包成一个新变量称为PC ==> 多(变量) 到 (组合)一(主成分),线性组合
因子分析的出发点是 找出引起相关变量变异的共同原因 ==> 一(因子) 到(引发) 多(变量),拆开然后归纳的过程
brief
模型可以用如下方式表达:

判断需要提取的因子数
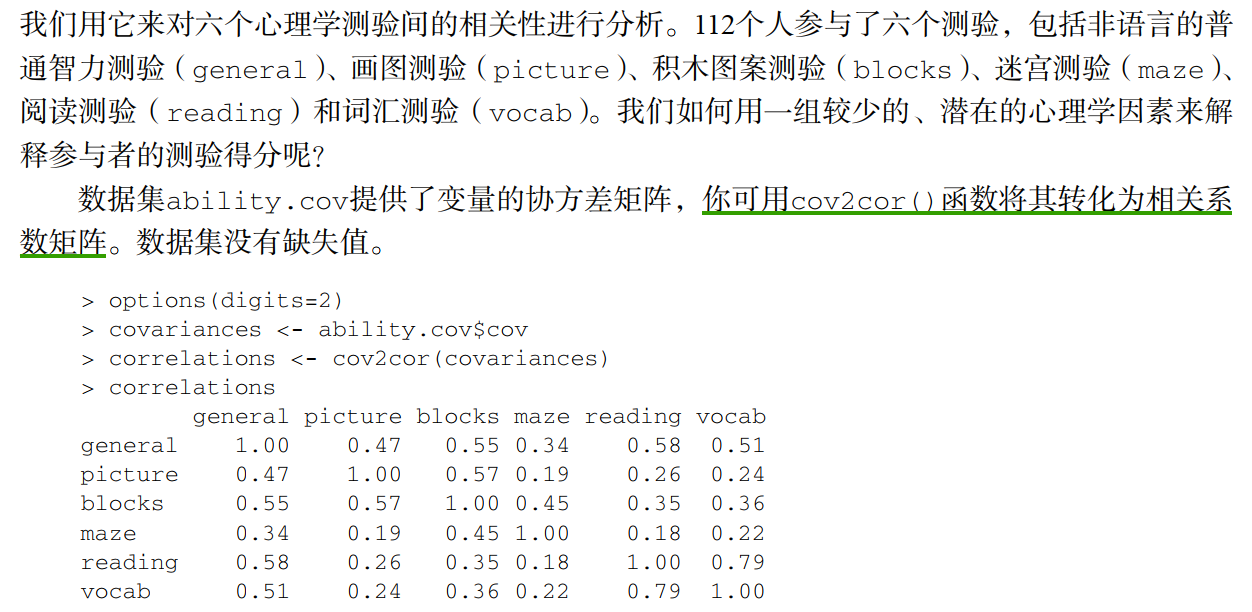
fa.parallel()函数可以判断提取的因子数
library(psych)
options(digits=2)
covariances <- ability.cov$cov
correlations <- cov2cor(covariances)
correlationsfa.parallel(correlations, n.obs=112, fa="both", n.iter=100,main="Scree plots with parallel analysis") # fa="both" 同时显示主成分和因子分析的结果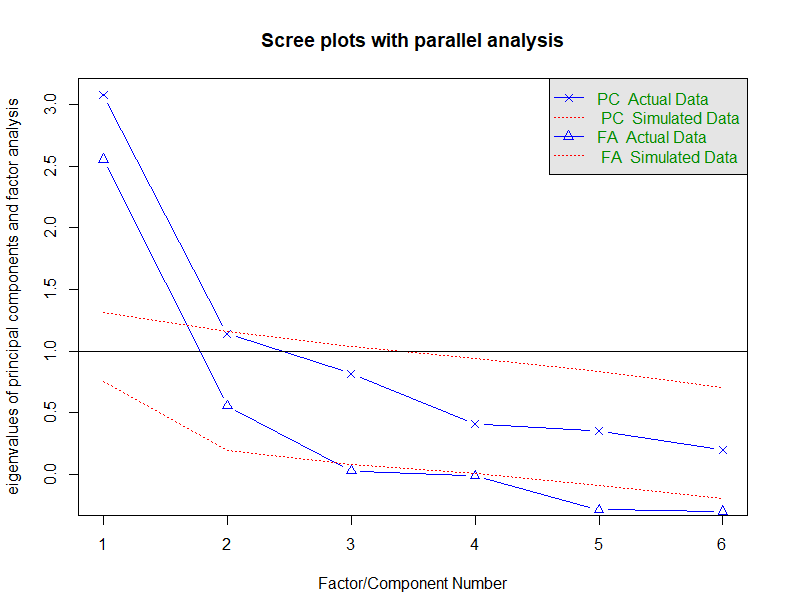
碎石图显示拐点在2/3个因子处
平行分析(红色虚线)显示三个因子时真实数据的特征值小于模拟数据的特征值
综合来看选择2个因子
提取公共因子


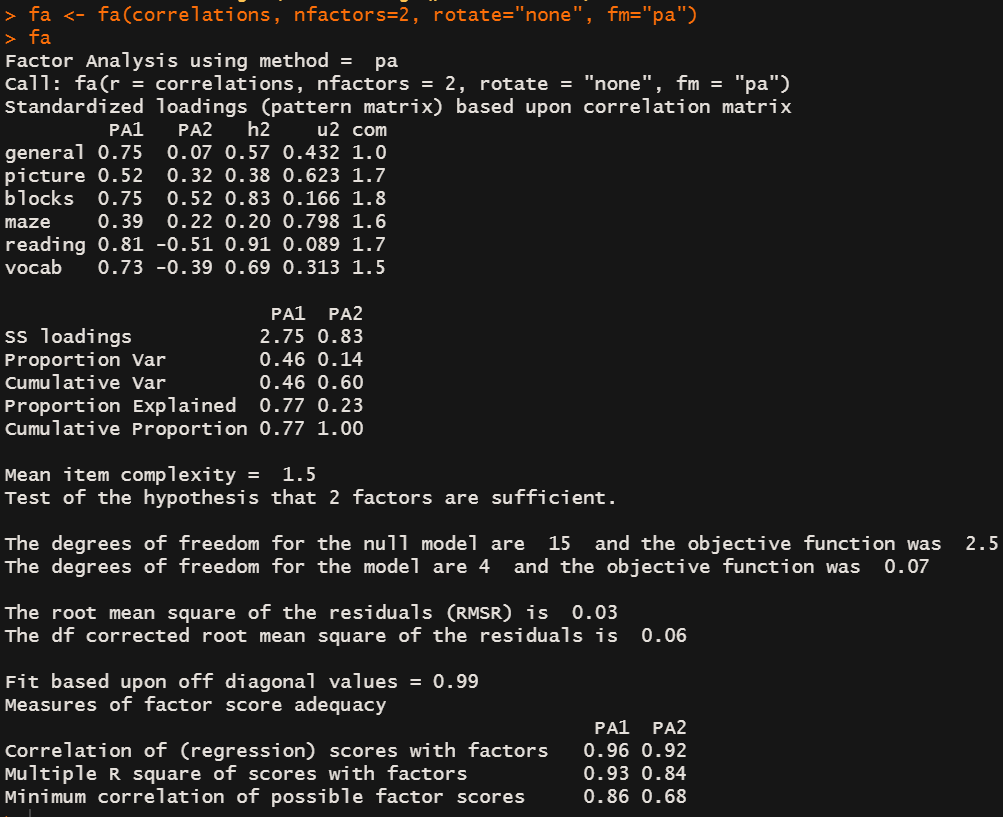
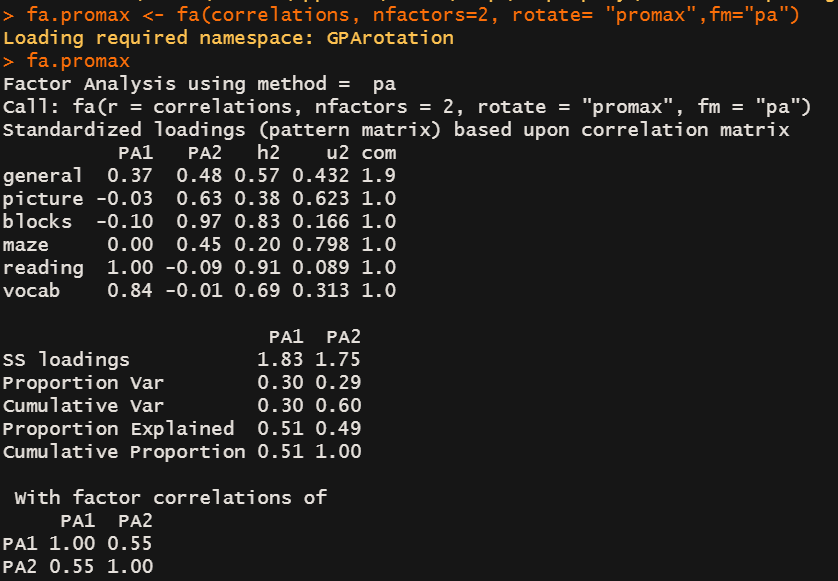
比如 Xvocab = 0.73PA1 - 0.39PA2 + Uvocab 解释
PA1 + PA2累积可以解释数据60%的变异
因子旋转
-
正交旋转
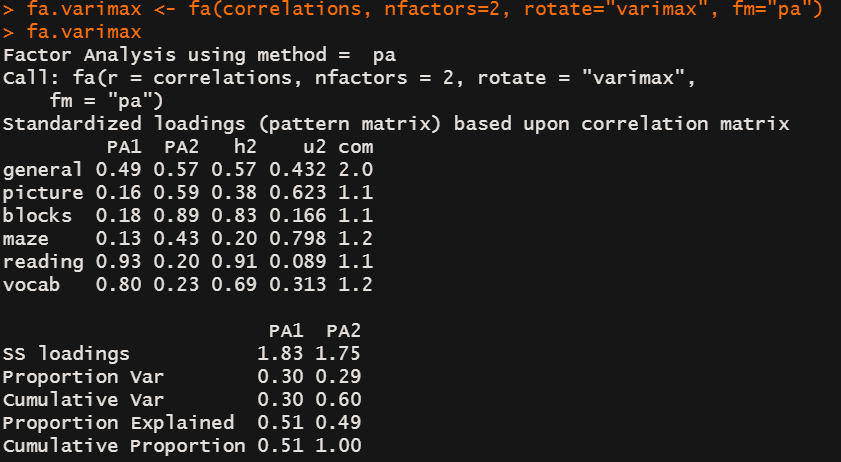
正交就是让PA1 与PA2不相关
现在PA1可以更多解释reading 和 vocab
PA2可以更好的解释picture blocks,但是累积解释方差不变。 -
斜交旋转
-
可视化方法
factor.plot(fa.varimax, labels=rownames(fa.varimax$loadings))
fa.diagram(fa.promax, simple=FALSE)
提取因子得分

相关文章:

R -- 用psych包做因子分析
因子分析 因子分析又称为EFA,是一系列用来发现一组变量的潜在结构的办法。它通过寻找一组更小的,潜在的结构来解释已观测到的显式的变量间的关系。这些虚拟的、无法观测的变量称为因子(每个因子被认为可以解释多个观测变量间共有的方差&…...

既然操作系统层已经提供了page cache的功能,为什么还要在应用层加缓存?
Page Cache是一种在操作系统内核中实现的缓存机制,用于缓存文件系统中的数据块。当一个进程请求读取一个文件时,操作系统会首先在Page Cache中查找数据块,如果找到了相应的数据块,则直接返回给进程;如果没有找到&#…...
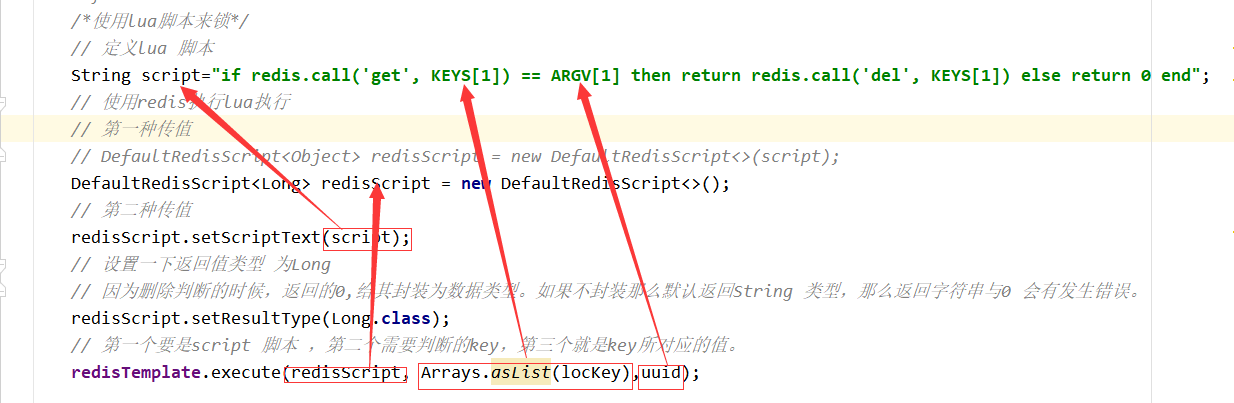
Redis应用问题解决
16. Redis应用问题解决 16.1 缓存穿透 16.1.1 问题描述 key对应的数据在数据源并不存在,每次针对此key的请求从缓存获取不到,请求都会压到数据源,从而可能压垮数据源。比如用一个不存在的用户id获取用户信息,不论缓存还是数据库…...

Qemu虚拟机读取物理机的物理网卡的流量信息方法
项目背景: 比如我有三个项目 A,B,C;其中A项目部署在物理机上,B,C项目部署在 虚拟机V1,V2中,三个项目接口需要相互调用。 需要解决的问题点: 1,因为A,B&#x…...
面试题之vue的响应式
文章目录前言一、响应式是什么?二、Object.defineProperty二、简单模拟vue三、深度监听四、监听数组总结前言 为了应对面试而进行的学习记录,可能不够有深度甚至有错误,还请各位谅解,并不吝赐教,共同进步。 一、响应式…...

聚焦弹性问题,杭州铭师堂的 Serverless 之路
作者:王彬、朱磊、史明伟 得益于互联网的发展,知识的传播有了新的载体,使用在线学习平台的学生规模逐年增长,越来越多学生在线上获取和使用学习资源,其中教育科技企业是比较独特的存在,他们担当的不仅仅是…...
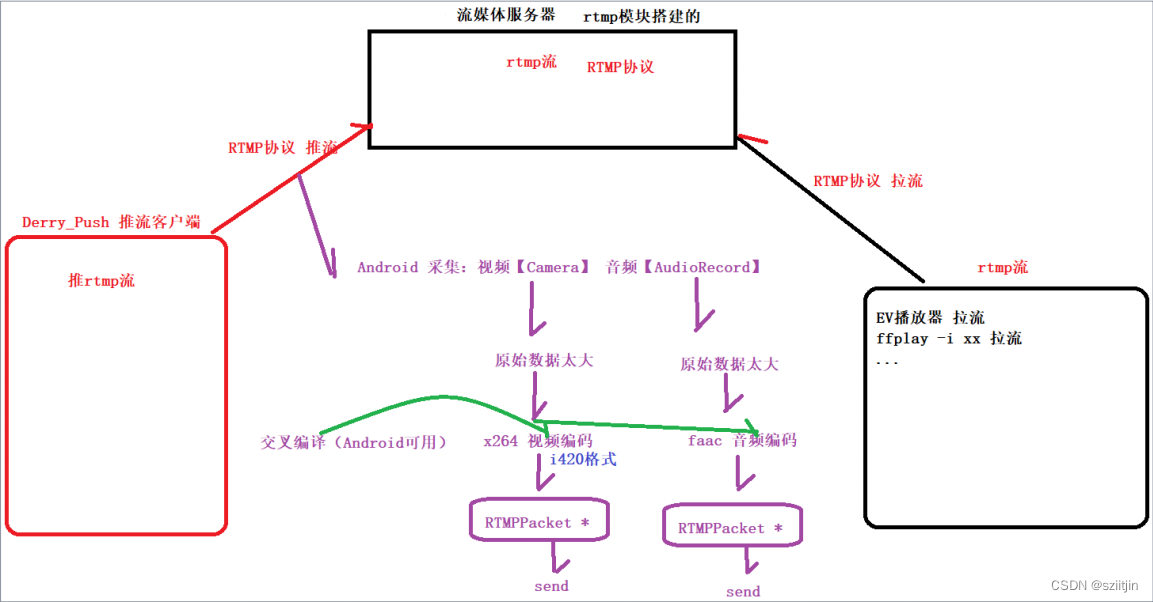
NDK RTMP直播客户端二
在之前完成的实战项目【FFmpeg音视频播放器】属于拉流范畴,接下来将完成推流工作,通过RTMP实现推流,即直播客户端。简单的说,就是将手机采集的音频数据和视频数据,推到服务器端。 接下来的RTMP直播客户端系列ÿ…...

Python3--垃圾回收机制
一、概述 Python 内部采用 引用计数法,为每个对象维护引用次数,并据此回收不在需要的垃圾对象。由于引用计数法存在重大缺陷,循环引用时由内存泄露风险,因此Python还采用 标记清除法 来回收在循环引用的垃圾对象。此外,…...
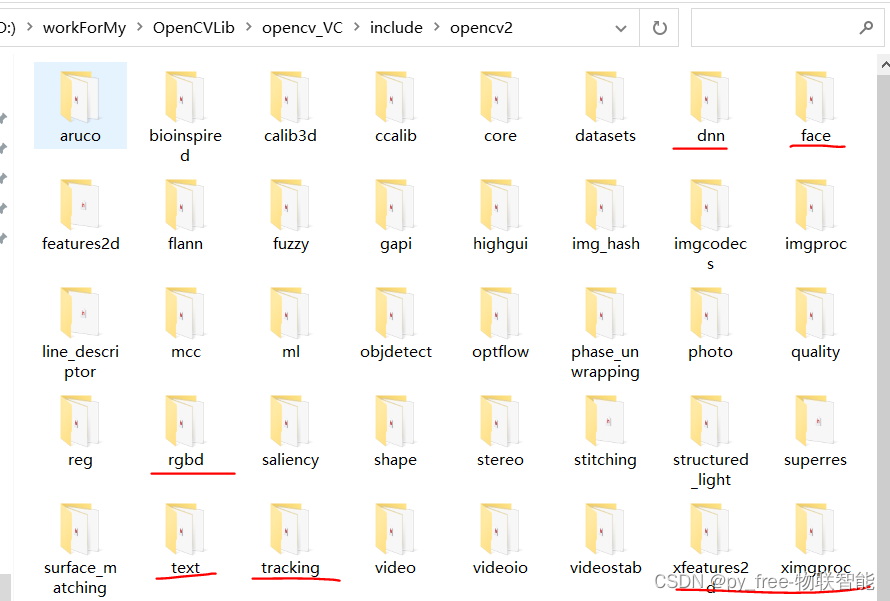
C/C++开发,认识opencv各模块
目录 一、opencv模块总述 二、opencv主要模块 2.1 opencv安装路径及内容 2.2 opencv模块头文件说明 2.3 成熟OpenCV主要模块 2.4 社区支持的opencv_contrib扩展主要模块 2.5 关于库文件的引用 一、opencv模块总述 opencv的主要能力在于图像处理,尤其是针对二维图…...
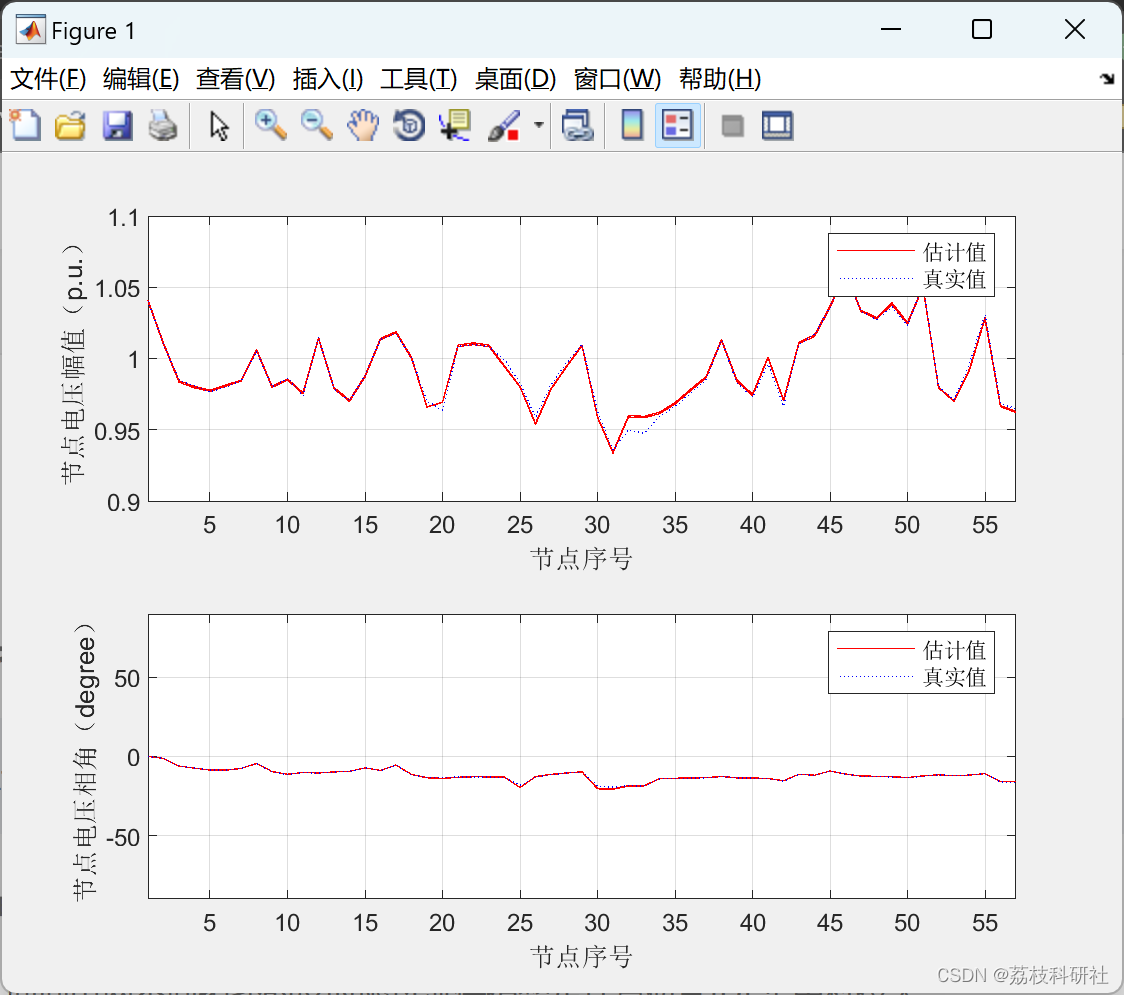
【WLSM、FDM状态估计】电力系统状态估计研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

准备2023(2024)蓝桥杯
前缀和 一维前缀和 s[i]s[i-1]a[i]二维前缀和(子矩阵的和) s[i][j]s[i-1][j]s[i][j-1]-s[i-1][j-1]a[i][j] 差分 一维数组 //b是差分数组b[i]c;b[j1]-c;例题 #include<iostream> using namespace std; int n,m; int b[100002],a[100002]; vo…...

剑指 Offer 60. n个骰子的点数
剑指 Offer 60. n个骰子的点数 难度:middle\color{orange}{middle}middle 题目描述 把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。 你需要用一个浮点数数组返回答案,其中第 i 个…...

阿里巴巴-淘宝搜索排序算法学习
模型效能:模型结构优化 模型效能:减枝 FLOPS:每秒浮点运算的次数 模型效能:量化 基于统计阈值限定,基于学习阈值限定。 平台效能:一站式DL训练平台 平台效能:搜索模型的系统流程 协同关系…...

〖Python网络爬虫实战⑮〗- pyquery的使用
订阅:新手可以订阅我的其他专栏。免费阶段订阅量1000python项目实战 Python编程基础教程系列(零基础小白搬砖逆袭) 说明:本专栏持续更新中,目前专栏免费订阅,在转为付费专栏前订阅本专栏的,可以免费订阅付费…...
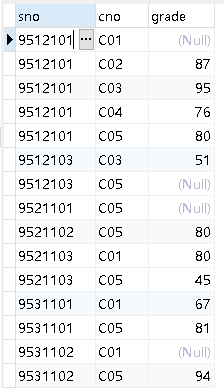
SQL综合查询下
SQL综合查询下 目录SQL综合查询下18、查询所有人都选修了的课程号与课程名题目代码题解19、SQL查询:查询没有参加选课的学生。题目代码20、SQL查询:统计各门课程选修人数,要求输出课程代号,课程名,有成绩人数ÿ…...

全连接层FC
lenet结构: 输入层(Input Layer):接收手写数字的图像数据,通常是28x28的灰度图像。 卷积层1(Convolutional Layer 1):对输入图像进行卷积操作,提取低级别的特征,使用 6 个大小为 5x5 的卷积核进行卷积,得到 6 个输出特征图,激活函数为 Sigmoid。 平均池化层1(Aver…...

图的遍历及连通性
文章目录 图的遍历及连通性程序设计程序分析图的遍历及连通性 【问题描述】 根据输入的图的邻接矩阵A,判断此图的连通分量的个数。 【输入形式】 第一行为图的结点个数n,之后的n行为邻接矩阵的内容,每行n个数表示。其中A[i][j]=1表示两个结点邻接,而A[i][j]=0表示两个结点无…...
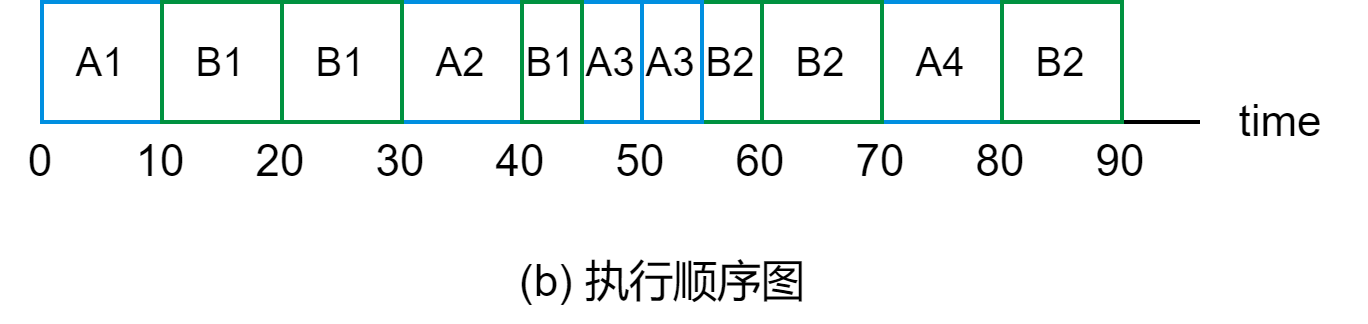
DJ3-4 实时调度
目录 3.4.1 实现实时调度的基本条件 1. 提供必要的信息 2. 系统的处理能力强 3. 采用抢占式调度机制 4. 具有快速切换机制 3.4.2 实时调度算法的分类 1. 非抢占式调度算法 2. 抢占式调度算法 3.4.3 常用的几种实时调度算法 1. 最早截止时间优先 EDF(Ea…...
)
Oracle之PL/SQL游标练习题(三)
游标练习题目1、定义游标:列出每个员工的姓名部门名称并编程显示第10个到第20个记录2、定义游标:从雇员表中显示工资大于3000的记录,只要姓名、部门编号和工资,编程显示其中的奇数记录3、用游标显示所有部门编号与名称,…...
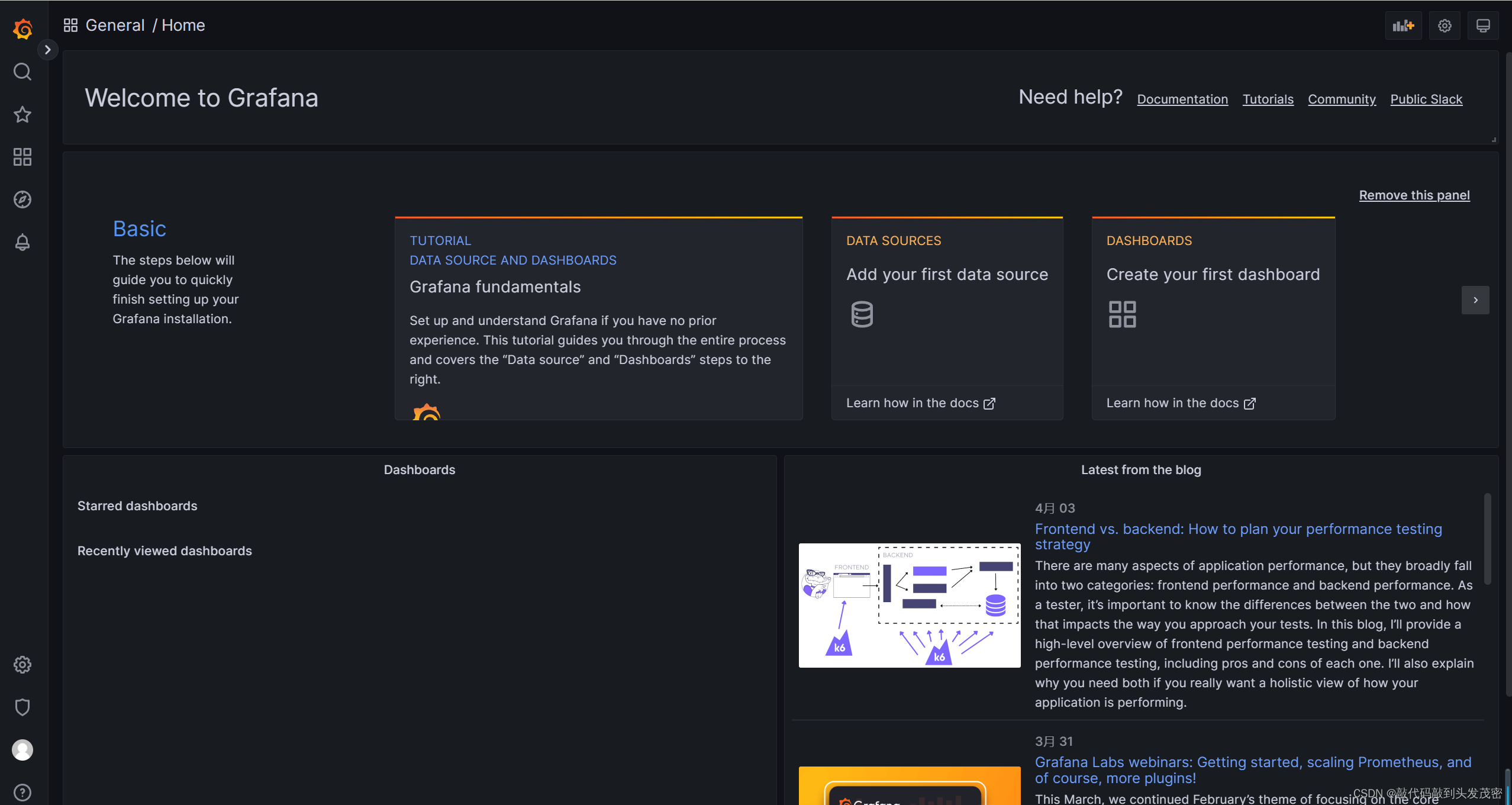
docker运行服务端性能监控系统Prometheus和数据分析系统Grafana
文章目录一、Prometheus的安装和运行1、使用docker拉取镜像2、创建prometheus.yml文件3、启动容器4、查看启动是否成功5、记录安装过程中出现的错误二、Grafana的安装和运行1、使用docker拉取镜像2、创建grafana3、运行grafana4、查看grafana运行日志5、登录grafana一、Prometh…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
