C++回溯算法---图的m着色问题01
C++回溯算法---图的m着色问题
图的m着色问题是指给定一个图以及m种不同的颜色,尝试将每个节点涂上其中一种颜色,使得相邻的节点颜色不相同。这个问题可以转化为在解空间树中寻找可行解的问题,其中每个分支结点都有m个儿子结点,最底层有m的n次方个叶子结点。算法的思路是在解空间树中做深度优先搜索,并使用约束条件来剪枝优化搜索。
代码:
#include <iostream>
#include <cstring>
/*
* 图的m着色问题
*/
using namespace std;const int maxn = 1005;
int G[maxn][maxn], color[maxn];//用于存储图中的边--用于存储每个节点的颜色
int n, m; //n表示图中节点的数量,m表示可供选择的颜色数目。bool ok(int u, int c) {for (int i = 1; i <= n; i++) {if (G[u][i] == 1 && color[i] == c)return false;}return true;
}bool dfs(int u) {if (u > n)return true;for (int i = 1; i <= m; i++) {if (ok(u, i)) {color[u] = i;if (dfs(u + 1))return true;color[u] = 0;}}return false;
}int main() {memset(G, 0, sizeof(G));//初始化邻接矩阵为0memset(color, 0, sizeof(color));//初始化颜色为0int e;//e表示图中边的数量cin >> n >> e >> m;for (int i = 0; i < e; i++) {int u, v;cin >> u >> v;G[u][v] = G[v][u] = 1;}if (dfs(1)) {cout << "Yes" << endl;for (int i = 1; i <= n; i++) {cout << "结点 " << i << " 的颜色为: " << color[i] << endl;}}else {cout << "No" << endl;}return 0;
}
分析:
这个算法的实现包括两个主要步骤:
- 判断颜色是否符合要求
对于每个节点 u,如果它与另一个节点 v 有边相连,且这两个节点颜色相同,那么就不能把节点 u 涂为该颜色。因此,需要定义一个函数
ok()来判断某个节点染上某种颜色是否符合要求。具体来说,ok(u, c)函数返回值为true表示节点 u 可以涂上颜色 c,否则返回false。2.使用深度优先搜索
使用深度优先搜索(DFS)从解空间树的根节点开始搜索,并在每个分支结点处调用
ok()函数来剪枝。如果在整棵解空间树中找到了一组可行解,那么算法就停止搜索并输出结果。如果找不到任何一个可行解,则算法输出无解信息。具体实现过程:
首先,需要定义一个二维数组 G[ ][ ],用于存储图中的边。其中,G[u][v] == 1 表示节点 u 和节点 v 之间有边相连,反之为 0。同时,还需要定义一个一维数组 color[ ],用于存储每个节点的颜色。
首先将所有边权赋值为 0,即不存在边。然后,读入所有边,将对应的边权赋值为 1。读入颜色数 m,并从节点 1 开始做深度优先搜索,依次尝试给每个节点涂上不同的颜色。在每个分支结点处,使用
ok()函数来判断是否符合要求。如果染色成功,则继续对下一个节点做深度优先搜索。如果找到了一组可行解,则输出结果。
运行结果:
问题描述
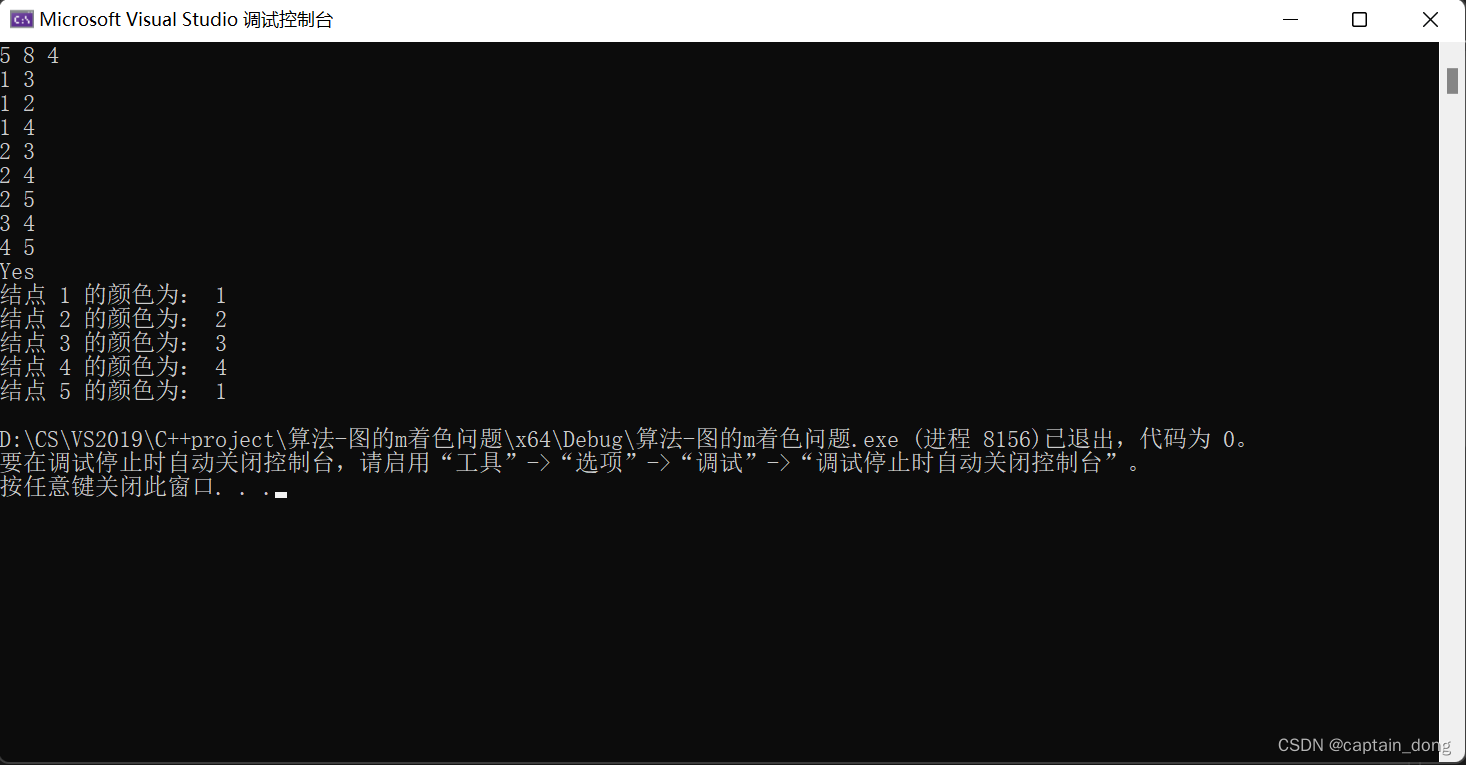
给定无向连通图G=(V, E)和m种不同的颜色,用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中相邻的两个顶点有不同的颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的两个顶点着不同颜色,则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
例如:点个数n=7,颜色m=3的涂色方案
算法设计
一般连通图的可着色问题,不仅限于可平面图。
给定图G=(V,E)和m种颜色,如果该图不是m可着色,给出否定回答;若m可着色,找出所有不同着色方法。
算法思路
设图G=(V, E), |V|=n, 颜色数= m, 用邻接矩阵a表示G, 用整数1, 2…m来表示
m种不同的颜色。顶点i所着的颜色用x[i]表示。
问题的解向量可以表示为n元组x={ x[1],…,x[n] }. x[i]∈{1,2,…,m},
解空间树为排序树,是一棵n+1层的完全m叉树.
在解空间树中做深度优先搜索, 约束条件:如果a[j][i]=1 , x[i] ≠ x[j]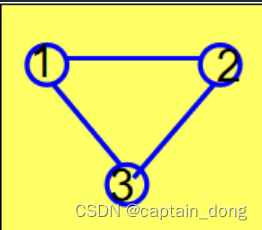

m=3,n=3时的解空间树
再举个例子
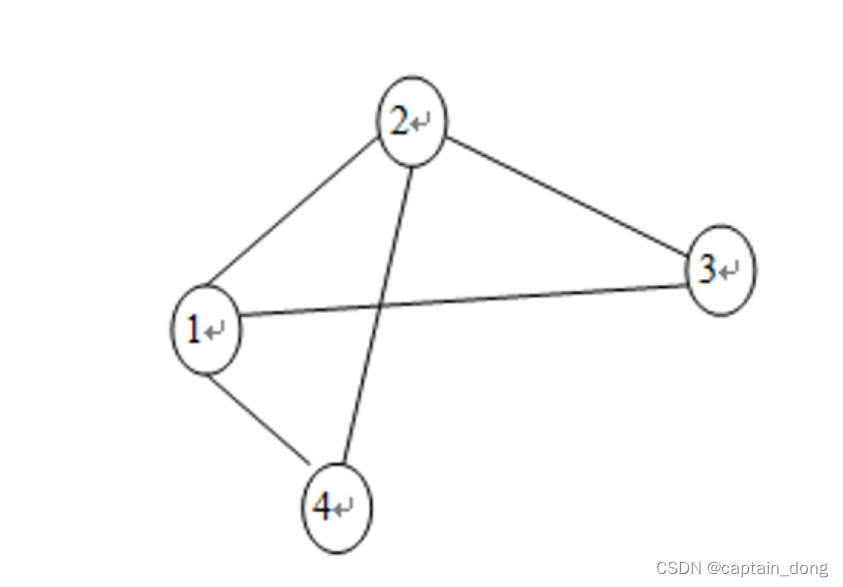
对于下图,写出图着色算法得出一种着色方案的过程。
顶点数量n=4, 色数:m=3
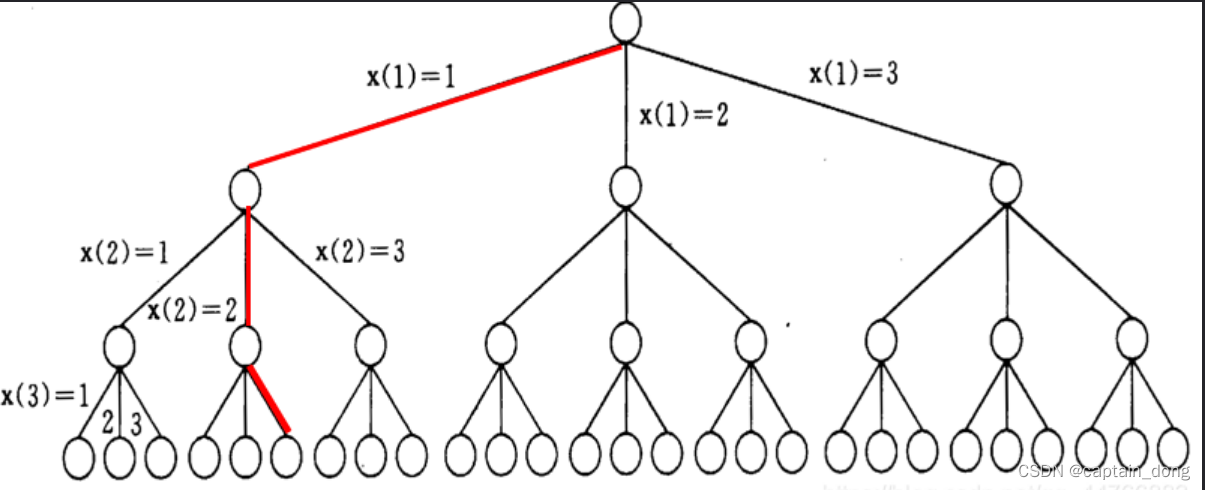
m=4,n=3时的解空间树
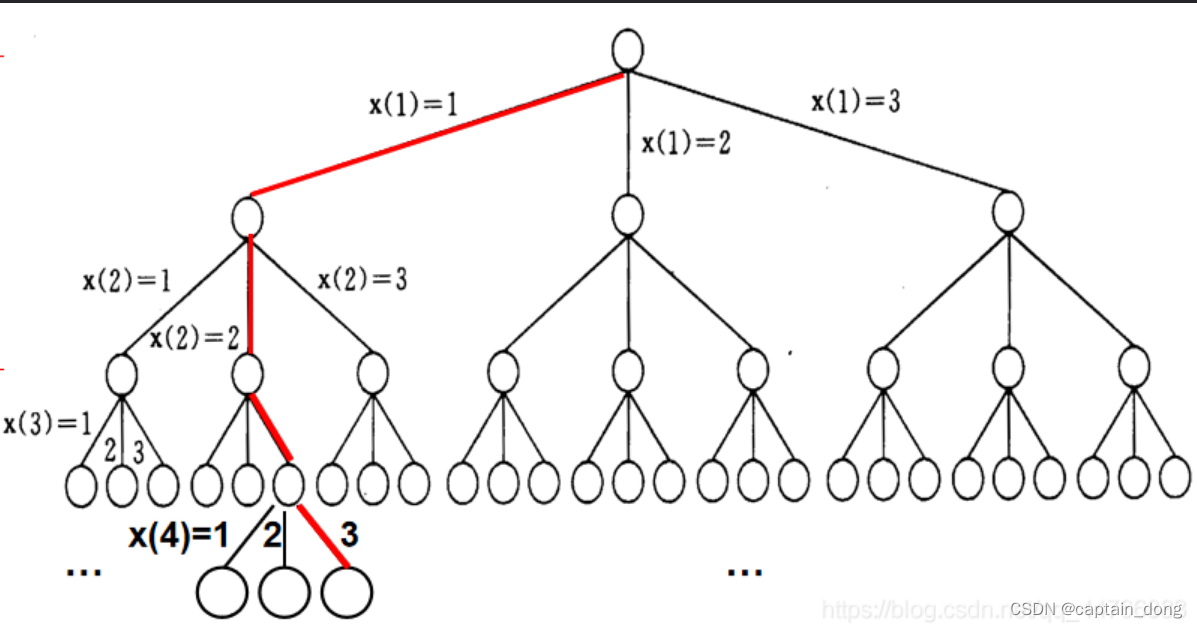
X[1]←1 , 返回 true
X[2]←1, 返回false; X[2]←2, 返回 true
X[3]←1 ,返回false; X[3]←2, 返回false;X[3]←3, 返回 true
X[4]←1, 返回false; X[4]←2, 返回false;X[4]←3, 返回 true
着色方案:(1,2,3,3)
复杂度分析
图m可着色问题的解空间树中,内结点个数是:
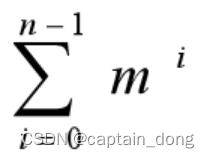
对于每一个内结点,在最坏情况下,用ok检查当前扩展结点每一个儿子的颜色可用性需耗时O(mn)。
因此,回溯法总的时间耗费是
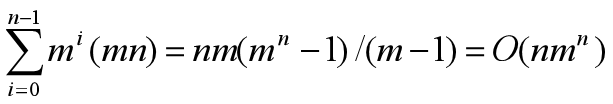
#include"图的着色.h"const int NUM = 100;
int n;//顶点数
int m;//颜色数
int a[NUM][NUM];//图的邻接矩阵
int x[NUM];//当前的解向量
int sum = 0;//解的数量bool same(int t) {int i;for (i = 1; i < n; i++) {//修正同色判断函数的循环范围if ((a[t][i] == 1) && (x[i] == x[t]))return false;}return true;
}void BackTrack(int t) {int i;if (t > n) {sum++;cout << "解" << sum << ":" << endl;//输出当前解的编号for (i = 1; i <= n; i++) {cout << x[i] << " ";//按照节点顺序输出颜色}cout << endl;}else{for (i = 1; i <= m; i++) {x[t] = i;if (same(t))BackTrack(t + 1);x[t] = 0;}}
}int main() {cin >> n >> m;//初始化邻接矩阵为0for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {a[i][j] = 0;}}//读入边,构建邻接矩阵int u, v;while (cin >> u >> v) {if (u < 1 || u > n || v < 1 || v > n) {//判断输入是否合法cout << "输入不合法!" << endl;continue;}a[u - 1][v - 1] = 1;a[v - 1][u - 1] = 1;}BackTrack(1);//从第1个节点开始cout << "一共有" << sum << "个解。" << endl;//输出解的数量return 0;
}
相关文章:
C++回溯算法---图的m着色问题01
C回溯算法---图的m着色问题 图的m着色问题是指给定一个图以及m种不同的颜色,尝试将每个节点涂上其中一种颜色,使得相邻的节点颜色不相同。这个问题可以转化为在解空间树中寻找可行解的问题,其中每个分支结点都有m个儿子结点,最底层…...
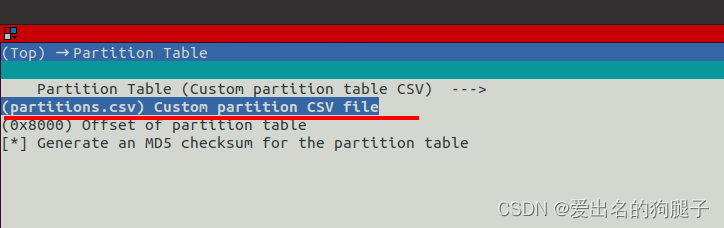
ESP32 分区表
ESP32 分区表 1. 分区表概述 ESP32 针对 flash 进行划分,划分为不同的区域用作不同的功能,并在flash的 0x8000 位置处烧写了一张分区表用来描述分区信息。 分区表可以根据自己的需要进行配置,每一个分区都有其特定的作用,可根据…...

JJJ-2 init_IRQ
void __init init_IRQ(void) {int ret;if (IS_ENABLED(CONFIG_OF) && !machine_desc->init_irq)irqchip_init();else // init_irq成员定义为imx6ul_init_irq,会走这个分支machine_desc->init_irq(); if (IS_ENABLED(CONFIG_OF) && IS_ENABLED…...

【NLP实战】基于Bert和双向LSTM的情感分类【下篇】
文章目录前言简介第一部分关于pytorch lightning保存模型的机制关于如何读取保存好的模型完善测试代码第二部分第一次训练出的模型的过拟合问题如何解决过拟合后记前言 本文涉及的代码全由博主自己完成,可以随意拿去做参考。如对代码有不懂的地方请联系博主。 博主…...

程序设计方法学
体育竞技分析 问题分析 体育竞技分析 需求:毫厘是多少? 如何科学分析体育竞技比赛? 输入:球员的水平 输出:可预测的比赛成绩 体育竞技分析:模拟N场比赛 计算思维:抽象 自动化 模拟&am…...

Hadoop之Yarn篇
目录 编辑 Yarn的工作机制: 全流程作业: Yarn的调度器与调度算法: FIFO调度器(先进先出): 容量调度器(Capacity Scheduler): 容量调度器资源分配算法࿱…...

Spring Cloud Nacos使用总结
目录 安装Nacos服务器 服务发现与消费 服务发现与消费-添加依赖 服务发现-配置文件 服务发现-注解 服务发现-Controller 服务消费-配置文件 服务消费-注解与Ribbon消费代码 服务消费-运行 配置管理 配置管理-添加依赖 配置管理-配置文件 配置管理-注解 配置管理-…...

目标检测框架yolov5环境搭建
目前,目标检测框架中,yolov5 是很火的,它基于pytorch框架,集成opencv等框架,项目地址:https://github.com/ultralytics/yolov5,对我来说,机器学习、深度学习才开始接触,本…...
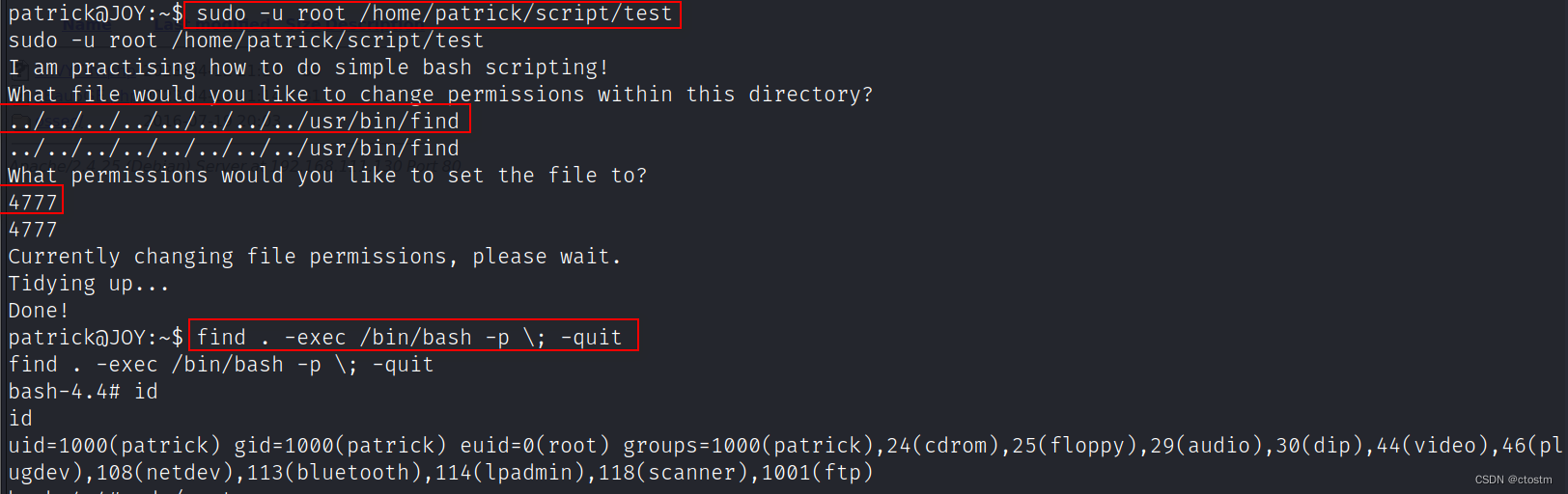
Vulnhub:Digitalworld.local (JOY)靶机
kali:192.168.111.111 靶机:192.168.111.130 信息收集 端口扫描 nmap -A -v -sV -T5 -p- --scripthttp-enum 192.168.111.130 使用enum4linux枚举目标smb服务,发现两个系统用户 enum4linux -a 192.168.111.130 ftp可以匿名登陆ÿ…...

STL源码剖析-六大部件, 部件的关系,复杂度, 区间表示
C标准库-体系结构与内核分析 根据源代码来分析 介绍 自学C侯捷老师的STL源码剖析的个人笔记,方便以后进行学习,查询。 为什么要学STL?按侯捷老师的话来说就是:使用一个东西,却不明白它的道理,不高明&…...

总有一个可用的连接,metaIPC1.2进入智能连接新时代
概述 metaIPC有1.0和2.0两个产品系列,2.0版本是可视对讲IPC,1.0新版本1.2在全面兼容ICE规范基础上进行了扩展,使metaIPC1.2进入智能化连接新时代。 metaIPC1.2在host/stun/turn/srs/zlm/janus/freeswitch等p2p/sfu/mcu进行全方位连通测试&a…...

棋盘问题c
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。 Input …...

华纳云:Linux系统下怎么创建普通用户并更改用户组
本篇内容主要讲解“Linux系统下怎么创建普通用户并更改用户组”,感兴趣的朋友不妨来看看。本文介绍的方法操作简单快捷,实用性强。下面就让小编来带大家学习“Linux系统下怎么创建普通用户并更改用户组”吧! 要求 项目做权限管理,不用root部…...

「她时代」背后的欧拉力量
2018年大热电视剧《北京女子图鉴》,讲述了一群在北京打拼的职业女性,她们背井离乡,被现实包裹,被压力、责任困扰,但依旧用倔强的个性、不屈的进取心和深厚的知识技能努力营造、交织出一片励志的天空,既激昂…...

kubespray v2.21.0 在线部署 kubernetes v1.24.0 集群【2】
文章目录创建 虚拟机模板虚拟机名称配置静态地址配置代理yum 配置配置主机名安装 git安装 docker安装 ansible配置内核参数安装 k8s定制安装新增节点配置主机名配置代理配置互信更新 inventory报错kubespray v2.21.0 部署 kubernetes v1.24.0 集群 【1】在 Rocky linux 8.7 使用…...

聚焦运营商信创运维,美信时代监控易四大亮点值得一试!
2021年11月《“十四五”信息通信行业发展规划》提出,到2025年,我国将建立高速泛在、集成互联、智能绿色、安全可靠的新型数字基础设施体系。 此《规划》让我国运营商信创进一步加速,中国移动、中国电信、中国联通等都先后加入信创大军&#x…...

[python刷题模板] 博弈入门-记忆化搜索/dp/打表
[python刷题模板] 博弈入门-记忆化搜索/dp/打表 一、 算法&数据结构1. 描述2. 复杂度分析3. 常见应用4. 常用优化二、 模板代码1. 打表贪心的博弈2. 464. 我能赢吗3. Nim游戏--最最基础版n1。三、其他四、更多例题五、参考链接一、 算法&数据结构 1. 描述 博弈一直没…...
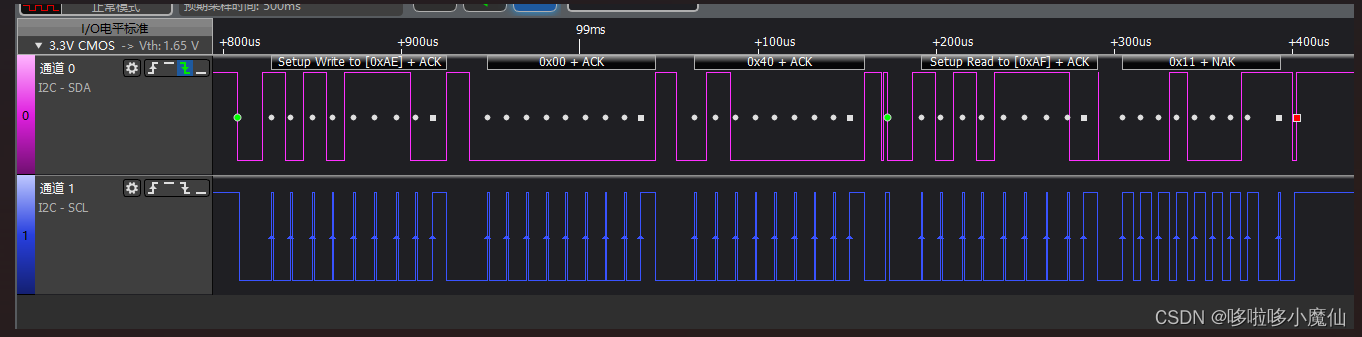
I2C通信
一、理论上了解I2C时序 I2C写数据时序如图: 通过解析器解析I2C通信如上图(SCL和SDA反了)。 1---起始信号 2、3---应答信号ACK 5---停止信号 起始信号:SCL线是高电平时,SDA线从高电平向低电平切换。 停…...
【Linux】man什么都搜不了,No manual entry for xxx的解决方案
本文首发于 慕雪的寒舍 man什么都搜不了,No manual entry for xxx的解决方案 系统 CentOS 7.6 1.问题描述 今天查手册的时候,发现man什么都查不了。不管是系统接口还是函数,都显示没有入口文档(No manual entry for)…...

STM32 库函数 GPIO_SetBits、GPIO_ResetBits、GPIO_WriteBit、GPIO_Write 区别
问题:当我使用STM32库函数对 I/O 口进行赋值时,在头文件中发现有四个相关的函数可以做这个操作,那么它们有什么区别呢? 一、GPIO_SetBits //eg: GPIO_SetBits(GPIOA, GPIO_Pin_1 | GPIO_Pin_2);解释:置位(置1)选择的数…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
