【Leetcode】消失的数字 [C语言实现]

👻内容专栏:《Leetcode刷题专栏》
🐨本文概括: 面试17.04.消失的数字
🐼本文作者:花 碟
🐸发布时间:2023.4.10
目录
思想1:先排序再查找
思想2:异或运算
代码实现:
思想3:等差数列求和相减
代码实现:
点击跳转到Leetcode的OJ平台 17.04 消失的数字
题目:
数组
nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?int missingNumber(int* nums, int numsSize);
示例1:
示例2:
分析:
1.数组中经过排列后是一串有序列的整数,只不过序列中缺失了一个整数,题目需要让你找出这个缺失的数字。
2.时间复杂度要求允许在O(n)范围内。
思想1:先排序再查找
首先,我们就可以想到将数组nums里的元素进行排序,然后进行依次查找,如果下一个数不是上一个数+1得到的,那么上一个数+1就是我们要找的消失的数字。这题,按道理可以这么去写。
但是,观察各类常见的排序算法的时间复杂度详解图,最坏情况达不到我们该题要求的时间复杂度之内,在这里我们去运用排序,并不太合适。
| 类别 | 排序方法 | 时间复杂度 | ||
|---|---|---|---|---|
| 平均情况 | 最好情况 | 最坏情况 | ||
| 插入排序 | 直接插入 | O(n²) | O(n) | O(n²) |
| 希尔排序 | O(n¹·³) | O(n) | O(n²) | |
| 选择排序 | 直接排序 | O(n²) | O(n²) | O(n²) |
| 堆排序 | O(nlog₂n) | O(nlog₂n) | O(nlog₂n) | |
| 交换排序 | 冒泡排序 | O(n²) | O(n) | O(n²) |
| 快速排序 | O(nlog₂n) | O(nlog₂n) | O(n²) | |
| 归并排序 | O(nlog₂n) | O(nlog₂n) | O(nlog₂n) | |
| 基数排序 | O(d(r+n)) | O(d(n+rd)) | O(d(r+n)) | |
| 注:基数排序的复杂度中,r代表关键字的基数,d代表长度,n代表关键字的个数 | ||||
接下来,我们寻找其他方法击破此题。
思想2:异或运算
我们利用异或运算的规则(相同为0,相异为1),我可以先让一个变量x,初始值为0,与数组nums中numSize个元素进行异或运算,最后再与0 ~ numSize循环遍历的值进行异或,就能够得到是一个落单的数字,也就是我们最后要找的“消失的数字”
代码实现:
int missingNumber(int* nums, int numsSize){int i = 0;int x = 0;for(i = 0;i < numsSize;i++){x ^= nums[i];}for(i = 0;i <= numsSize;i++){x ^= i;}return x;
}思想3:等差数列求和相减
我们可以写一个循环计算0~numSize所有数字之和,0到numSize个数字本质也是一个等差数列,也可以使用等差数列求和公式,得出一个sum1值。继续求出nums数组中所有整数之和,得出一个sum2值。sum1减去sum2得到的数字就是“消失的数字”
代码实现:
int missingNumber(int* nums, int numsSize){int i = 0;int sum1 = (1 + numsSize)*numsSize / 2;int sum2 = 0;for(i = 0;i < numsSize;i++){sum2 += nums[i];}return sum1 - sum2;
}🤗🤗 好啦,本篇文章的创作就到此为止啦,如有不当,还请私信我纠正哦~
相关文章:

【Leetcode】消失的数字 [C语言实现]
👻内容专栏:《Leetcode刷题专栏》 🐨本文概括: 面试17.04.消失的数字 🐼本文作者:花 碟 🐸发布时间:2023.4.10 目录 思想1:先排序再查找 思想2:异或运算 代…...

SpringBoot接口 - 如何实现接口限流之单实例
在以SpringBoot开发Restful接口时,当流量超过服务极限能力时,系统可能会出现卡死、崩溃的情况,所以就有了降级和限流。在接口层如何做限流呢? 本文主要回顾限流的知识点,并实践单实例限流的一种思路。 SpringBoot接口 …...

【花雕学AI】深度挖掘ChatGPT角色扮演的一个案例—CHARACTER play : 莎士比亚
CHARACTER play : 莎士比亚 : 52岁,男性,剧作家,诗人,喜欢文学,戏剧,爱情 : 1、问他为什么写《罗密欧与朱丽叶》 AI: 你好,我是莎士比亚,一位英国的剧作家和诗人。我很高兴你对我的…...

腾讯云物联网开发平台 LoRaWAN 透传接入 更新版
前言 之前有一篇文章介绍LoRaWAN透传数据,不过还是用物模型云端数据解析脚本,不是真正的透传。腾讯云物联网开发平台也支持对LoRaWAN原始数据的透传、转发。今天来介绍下。腾讯云 IoT Explorer 是腾讯云主推的一站式物联网开发平台,IoT 小能手…...

4.6--计算机网络之TCP篇之TCP的基本认识--(复习+深入)---好好沉淀,加油呀
1.TCP 头格式有哪些? 序列号: 在建立连接时由计算机生成的随机数作为其初始值,通过 SYN 包传给接收端主机,每发送一次数据,就「累加」一次该「数据字节数」的大小。 用来解决网络包乱序问题。 确认应答号: …...
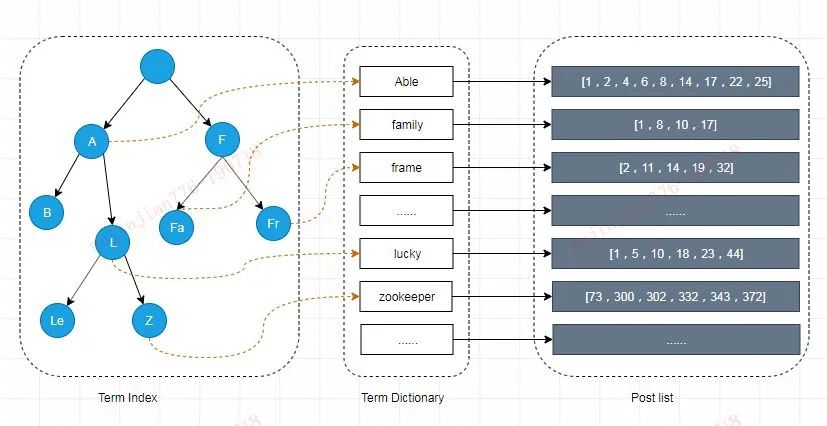
一文吃透Elasticsearch
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址 如果访问不了Github,…...
CPU占用率高怎么办?正确解决方法在这里!
案例:CPU占用率高怎么解决 【各位朋友,我的电脑现在运行太慢了,同事说可能是CPU占用率太高了,但对本电脑小白来说,完全不知道怎么处理,大家有什么好的方法可以解决这个问题吗?】 在计算机中&a…...

ChatGPT实现用C语言写一个学生成绩管理系统
随着ChatGPT爆火,大家都在使用ChatGPT来帮助自己提高效率,对于程序员来说使用它来写代码怎么样呢?今天尝试让ChatGPT,写了一个学生成绩管理系统。 问题是:使用C语言写一个学生成绩管理系统,要求使用链表&a…...

Swagger文档注释
本文以DRF框架为例使用 为什么要接口文档注释 一. 方便后端调试与后续接口更新; 二. 对于大型前后端分离项目,前后端人员是分开开发的,甚至前端的人你都不知道远在何处,这时候接口文档的重要性就太重要了。 三. 接口注释文档常用…...
pdf怎么转换ppt格式,两个方法转换
PDF作为一种常用的文件格式,被大众所熟悉。虽然PDF具备的稳定性,安全性,以及很强的兼容性可以让我们更方便顺畅的阅读PDF文件,但若是有需要展示PDF文件内容的时候,其优点就没有那么凸显了,这时还是将pdf转换…...

深度学习编译器相关的优秀论文合集-附下载地址
公司排名不分先后 目前在AI芯片编译器领域,有很多大公司在进行研究和开发。以下是一些主要的公司和它们在该领域的研究时间: 英伟达(NVIDIA):英伟达是一家全球知名的图形处理器制造商,其在AI芯片编译器领域…...
vue全局使用svg
1、安装依赖 npm install svg-sprite-loader2、配置选项 在vue.config.js的chainWebpack里配置下面代码 解释:config.module.rule是一个方法,用来获取某个对象的规则。.exclude.add(文件a)是往禁用组添加文件a,就是对文…...

每天一点C++——杂记
结构体的深拷贝和浅拷贝 浅拷贝就是只拷贝指针,并不拷贝指针所指向的内容,深拷贝则会对指针的内容进行拷贝。浅拷贝会在一些场景下出现问题,看下面的例子: struct s {char * name;int age; };如果我定义 一个对象s1,…...

Document Imaging SDK 11.6 for .NET Crack
Document Imaging SDK for .NET View, Convert, Annotate, Process,Edit, Scan, OCR, Print 基本上被认为是一种导出 PDF 解决方案,能够为用户和开发人员提供完整且创新的 PDF 文档处理属性。它具有提供简单集成的能力,可用于增强用户 .NET 的文档成像程…...
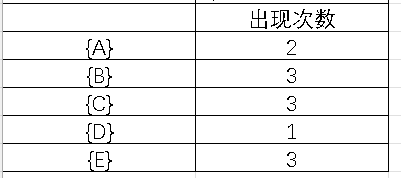
数据挖掘(3.1)--频繁项集挖掘方法
目录 1.Apriori算法 Apriori性质 伪代码 apriori算法 apriori-gen(Lk-1)【候选集产生】 has_infrequent_subset(c,Lx-1)【判断候选集元素】 例题 求频繁项集: 对于频繁项集L{B,C,E},可以得到哪些关联规则: 2.FP-growth算法 FP-tre…...

2023年信息安全推荐证书
随着网络安全行业的不断升温,相关的认证数量也不断增加,对于在网络安全行业发展的人才来说,提升职业竞争力最有效的办法之一,就是取得权威认证。 那么如何从繁多的适合网络安全从业者的证书中选择含金量高、发展潜力大的证书&…...

基于ArcGIS、ENVI、InVEST、FRAGSTATS等多技术融合提升环境、生态、水文、土地、土壤、农业、大气等领域应用
【自选】 时间地点:2023年7月22日-28日【乌鲁木齐】时间地点:2023年8月12日-18日【福建泉州】 【六天实践教学、提供全部资料】 专题一、空间数据获取与制图 1.1 软件安装与应用讲解 1.2 空间数据介绍 1.3海量空间数据下载 1.4 ArcGIS软件快速入门…...
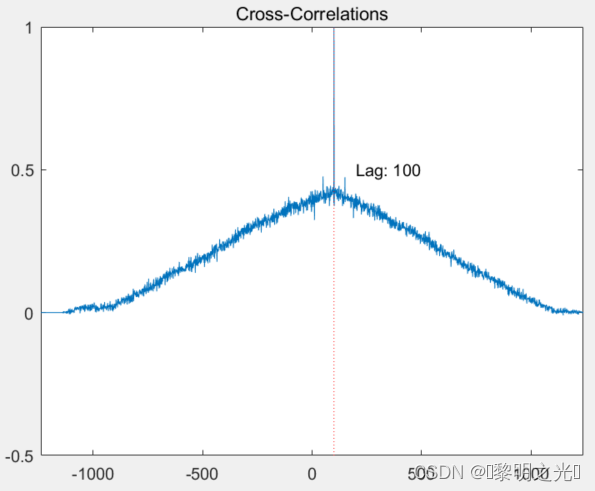
基于ZC序列的帧同步
Zadoff-Chu序列是一种特殊的序列,具有良好的自相关性和很低的互相关性,这种性能可以被用来产生同步信号,作为对时间和频率的相关运算在TD-LTE系统中,Zadoff-Chu(ZC)序列主要应用于上行RS序列生成、PRACH前导序列生成以及主同步信号…...

配置NFS服务器-debian
NFS(Network Files System)是网络文件系统的英文缩写,由Sun公司于1980年开发,用于在UNIX操作系统间实现磁盘文件共享。在Linux操作系统出现后,NFS被Linux继承,并成为文件服务的一种标准。 通过网络,NFS可以在不同文件…...

正点原子STEMWIN死机
在用正点原子STM32F4开发板,搭配对应的button历程时,发现运行一会,button都无法使用了,以为是emwin死机了,但是看到Led还在闪烁,排除系统死机问题。那就是emwin的任务没有运行起来,但是打断点后…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
