216、组合总数III
难度:中等
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
var combinationSum3 = function(k, n) {var result = []var path = []var backTracking = function(startIndex,sum){ //sum为收集的元素的和if(sum>n){ //剪枝条件1:sum>nreturn}if(path.length==k){if(sum==n){result.push(Array.from(path))//或result.push([...path]) 解构赋值}return}for(let i=startIndex;i<=9-(k-path.length)+1;i++){ //剪枝条件2:i<9-(k-path.length)+1 path.push(i)backTracking(i+1,sum+i) //i+1保证下一个选择的元素不会和已选择的元素重复path.pop()}}backTracking(1,0) //初始值从1开始加,sum初始值为0return result
};
相关文章:

216、组合总数III
难度:中等 找出所有相加之和为 n 的 k 个数的组合,且满足下列条件: 只使用数字1到9 每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 示例 1: 输入: k 3, n 7…...

简单的重装系统教程
郁闷,最近电脑一直蓝屏重启,用 2 分钟就蓝屏一次,遂产生重装系统的想法。 准备 U盘(8G或以上) PE 工具: 微PE工具箱快速指引 | 微PE优盘使用说明书 (wepe.com.cn) 系统镜像: 官网 Windows 10 官网 Windows 11 M…...

机器学习---集成学习报告
1.原理以及举例 1.1原理 集成学习(Ensemble Learning)是一种机器学习策略,它通过结合多个基学习器(base learners)的预测来提高模型的性能。集成学习的目标是创建一个比单个基学习器更准确、更稳定的最终预测模型。这…...
教你如何将PDF文件转换成PPT演示文稿
在工作和学习中,我们可能需要将一些PDF文件转换成PPT演示文稿,以便于更好地展示和分享。虽然PPT和PDF是两种不同的文档格式,但是我们可以使用一些专业的软件或在线工具来实现这种转换。下面就让我们来教你如何将PDF文件转换成PPT演示文稿。 …...

涨点技巧: 谷歌强势推出优化器Lion,引入到Yolov5/Yolov7,内存更小、效率更高,秒杀Adam(W)
1.Lion优化器介绍 论文:https://arxiv.org/abs/2302.06675 代码:automl/lion at master google/automl GitHub 1.1 简单、内存高效、运行速度更快 1)与 AdamW 和各种自适应优化器需要同时保存一阶和二阶矩相比,Lion 只需要动量,将额外的内存占用减半; 2)由于 Lion…...
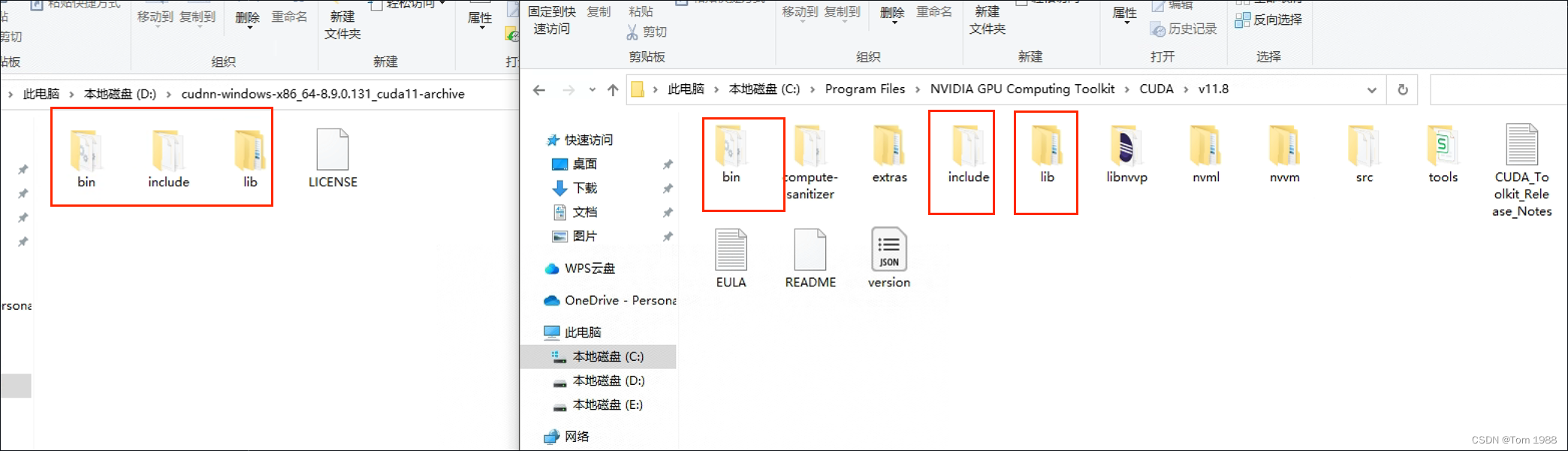
Windows GPU版本的深度学习环境安装
本文记录了cuda、cuDNN的安装配置。 参考文章: cuda-installation-guide-microsoft-windows 12.1 documentation Installation Guide :: NVIDIA cuDNN Documentation 一、cuda安装 注意事项: 1、cuda安装最重要的是查看自己应该安装的版本。 表格…...
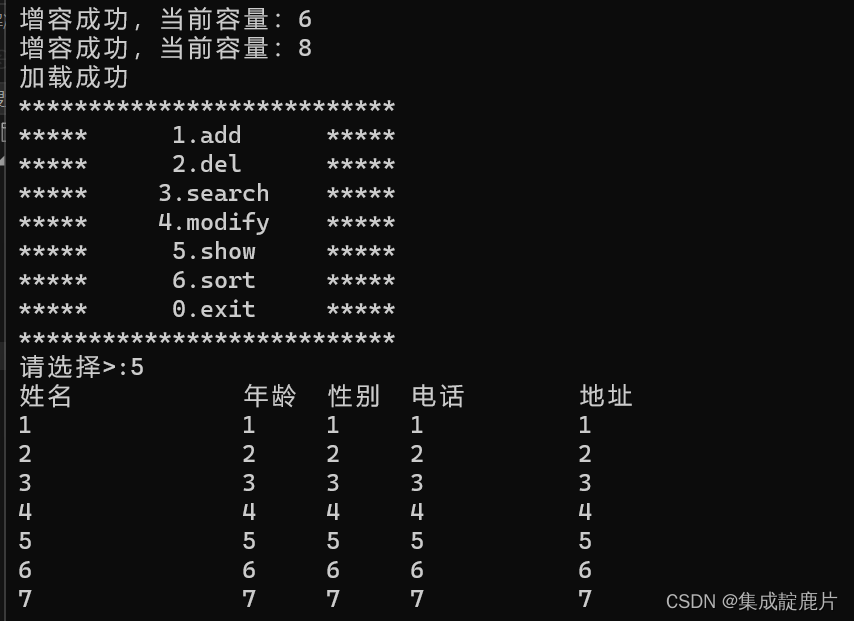
C语言实践——通讯录(3)(文件版)
首先感谢上一篇博客的大佬们的点赞,非常感谢!!! 目录 前言 一、需要添加的功能 1.增加保存数据函数——可以保存数据到文件中 主要逻辑: 注意事项: 代码实现: 2.修改初始化函数——新…...

GPT撑腰,微软再战谷歌 | 大厂集体抢滩ChatGPT:谁真的有实力,谁在试点商业化?
国内互联网大厂已经很久没有这样的盛况了! 在各自领域成长为头部的互联网大厂们,近年来正在向“自留地”的纵深发展,正面交锋的机会并不多。直到大洋彼岸传来GPT的声音后,一下子抓住了大厂们的G点,他们仿佛听到了新一轮…...
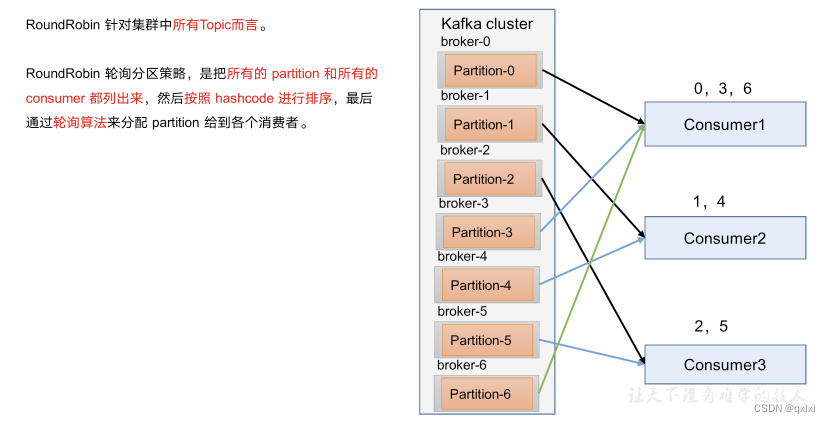
【消息队列】细说Kafka消费者的分区分配和重平衡
消费方式 我们直到在性能设计中异步模式,一般要么是采用pull,要么采用push。而两种方式各有优缺点。 pull :说白了就是通过消费端进行主动拉去数据,会根据自身系统处理能力去获取消息,上有Broker系统无需关注消费端的…...
——打印输出(详细语法参考 + 参数说明 + 具体示例)| 附:Python输出表情包)
【Python从入门到人工智能】14个必会的Python内置函数(7)——打印输出(详细语法参考 + 参数说明 + 具体示例)| 附:Python输出表情包
你仔细想想,你和谁在一起的时候,最放得开、最自然、最舒服,又毫无顾忌,可以做回真实的你。那个人才是你心里最特别,最重要的人。 🎯作者主页: 追光者♂🔥 🌸个人简介: 💖[1] 计算机专业硕士研究生💖 🌟[2] 2022年度博客之星人工智能领域TOP4�…...
为什么要创建FAQ?这篇文章告诉你
什么是FAQ 通过上述的引入大家应该也了解到了,FAQ是为了“解决问题”而存在的。FAQ是英文Frequently Asked Questions的缩写,中文意思就是“经常问到的问题”,或者更通俗地叫做“常见问题解答”。FAQ是当前网络上提供在线帮助的主要手段&…...

基于html+css的盒子展示1
准备项目 项目开发工具 Visual Studio Code 1.44.2 版本: 1.44.2 提交: ff915844119ce9485abfe8aa9076ec76b5300ddd 日期: 2020-04-16T16:36:23.138Z Electron: 7.1.11 Chrome: 78.0.3904.130 Node.js: 12.8.1 V8: 7.8.279.23-electron.0 OS: Windows_NT x64 10.0.19044 项目…...
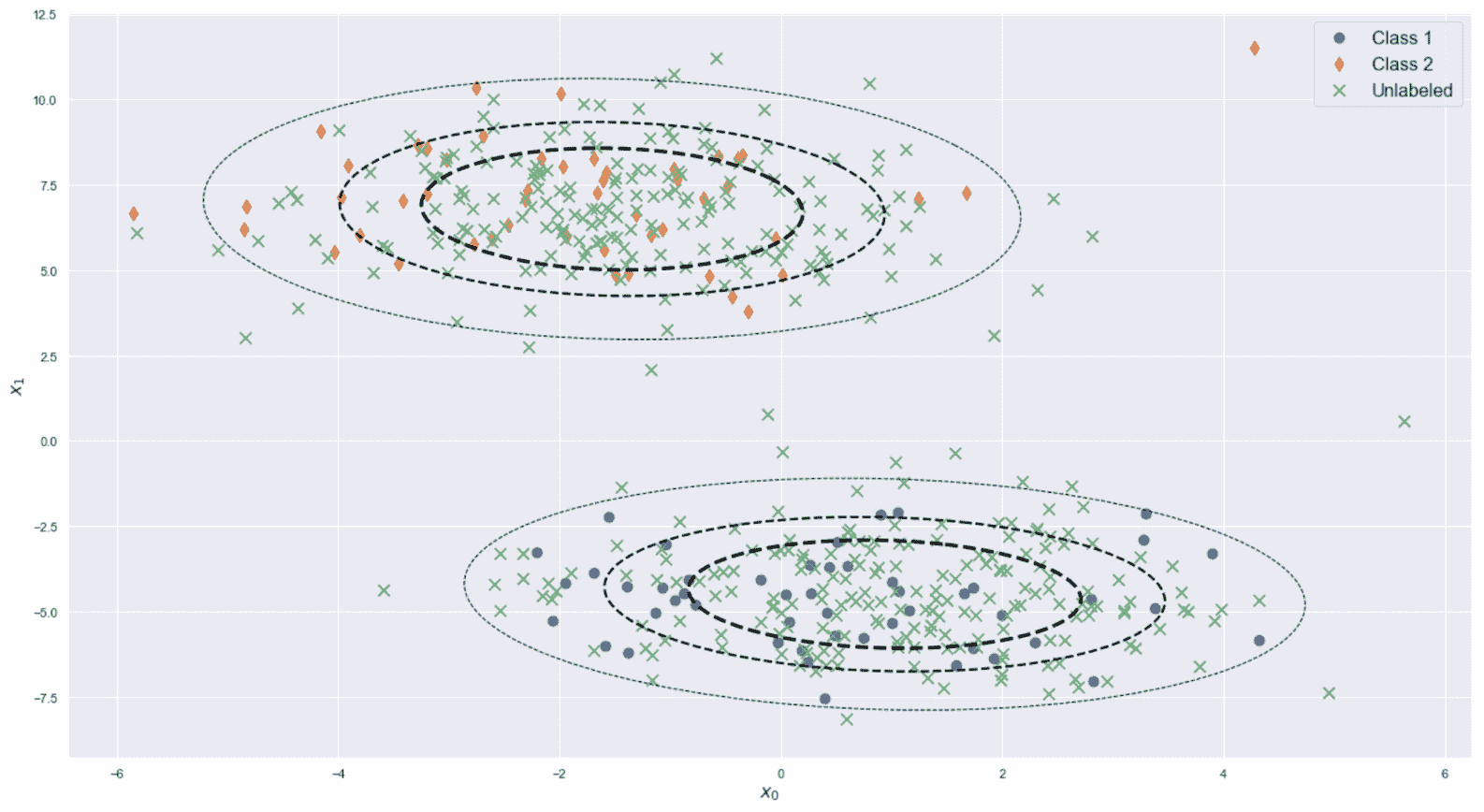
Python 无监督学习实用指南:1~5
原文:Hands-on unsupervised learning with Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关…...

2023 腾讯暑期实习申请经验分享
首先要向还在等我出 CMU 15-445 后面实验的同学们说声抱歉,这个系列可能暂时要停更啦。 一方面是博主最近课程和实验室方面的任务比较多,另一方面是有幸拿下了今年腾讯 WXG 后端开发的暑期实习 Offer,后面可能要提前学习一些工作中用到的框架…...

Protocol Buffers 介绍
Protocol Buffers Protocol Buffers ,协议缓冲区。什么是Protocol Buffers呢?或者我们简称PB 吧。那么Protocol Buffers 是一种与语言无关、与平台无关的可扩展机制,用于序列化结构化的数据。 example message Person {optional string nam…...

【模电实验】基尔霍夫定律、叠加定理和戴维南定理验证实验
实验目的 验证基尔霍夫电流定律(KCL)和电压定律(KVL)加深对该定理的理解验证叠加定理,加深对该定理的理解验证戴维南定理,掌握有源二端口网络的开路电压,短路电流和入端等效电阻的测定方法通过实…...

java某百货店POS积分管理系统_积分点更新生成以及通票回收处理
百货店是生活中不可缺少的一部分,为了给顾客提供更方便的服务平台以及更好的服务质量,而设计了POS积分管理系统。百货店通过点积分的管理获得顾客更好的信誉,增加客户流量,获得更多的利益。在百货店经营的过程中,每天的…...

Flutter 常用指令
1.flutter create app_01 :创建一个新的Flutter项目 2.flutter run:运行应用程序 3.flutter run -d <deviceId>:运行指定模拟器或者真机 4.flutter devices:查看计算机上的真机设备和IOS模拟器 5.flutter emulators&…...

定义全局变量property与getprop
authordaisy.skye的博客_CSDN博客-Qt,嵌入式,Linux领域博主 adb调试 adb shell getprop .adb logcat 报错 init: sys_prop: permission denied uid:1006 name:ro.camera.gc02m1 在linux驱动中查找 find ./ -name *.c | xargs grep -n "property_set" find ./ -n…...

双目三维测距(python)
文章目录 1. 双目检测1.1 调用相机1.2 分割画面 2. 双目标定2.1 相机标定2.2 获取参数 3. 双目测距3.1 立体校正3.1.1 校正目的3.1.2 校正方法3.1.2 相关代码 3.2 立体匹配和视差计算3.3 深度计算3.4 注意事项 4. 完整代码 代码打包下载: 链接1:https://…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

RFID推动新能源汽车零部件生产系统管理应用案例
RFID推动新能源汽车零部件生产系统管理应用案例 一、项目背景 新能源汽车零部件场景 在新能源汽车零部件生产领域,电子冷却水泵等关键部件的装配溯源需求日益增长。传统 RFID 溯源方案采用 “网关 RFID 读写头” 模式,存在单点位单独头溯源、网关布线…...

SpringSecurity+vue通用权限系统
SpringSecurityvue通用权限系统 采用主流的技术栈实现,Mysql数据库,SpringBoot2Mybatis Plus后端,redis缓存,安全框架 SpringSecurity ,Vue3.2Element Plus实现后台管理。基于JWT技术实现前后端分离。项目开发同时采 …...

compose 组件 ---无ui组件
在 Jetpack Compose 中,确实存在不直接参与 UI 渲染的组件,它们主要用于逻辑处理、状态管理或副作用控制。这些组件虽然没有视觉界面,但在架构中扮演重要角色。以下是常见的非 UI 组件及其用途: 1. 无 UI 的 Compose 组件分类 (…...
