机器学习---集成学习报告
1.原理以及举例
1.1原理
集成学习(Ensemble Learning)是一种机器学习策略,它通过结合多个基学习器(base learners)的预测来提高模型的性能。集成学习的目标是创建一个比单个基学习器更准确、更稳定的最终预测模型。这种方法可以减少过拟合、提高泛化能力,并在很多情况下,显著提高预测性能。
集成学习的主要原理包括:
多样性(Diversity):基学习器应该在某种程度上具有差异,从而降低它们共同犯错的概率。多样性可以通过使用不同的训练数据、不同的基学习算法或不同的参数设置来实现。
结合策略(Combining Strategy):集成学习需要一个合适的策略来结合基学习器的预测结果。常见的结合策略包括投票法(Majority Voting,用于分类任务)、平均法(Averaging,用于回归任务)和加权法(Weighted Voting/Averaging,根据基学习器的性能分配权重)。
集成学习的常见方法包括:
Bagging(Bootstrap Aggregating):通过自助采样(Bootstrap Sampling)的方法从原始数据集中抽取多个子集,并训练多个基学习器。最终预测结果通过投票(分类任务)或平均(回归任务)得到。
Boosting:Boosting 是一种迭代方法,每个基学习器在训练时对前一个学习器犯错的样本进行加权,从而关注这些难以分类或预测的样本。预测结果通过加权投票(分类任务)或加权平均(回归任务)得到。常见的 Boosting 算法包括 AdaBoost、Gradient Boosting 和 XGBoost。
Stacking(Stacked Generalization):训练多个基学习器,然后使用一个新的学习器(称为元学习器或次级学习器)将基学习器的输出作为输入进行训练。元学习器负责将这些基学习器的预测结果进行组合,生成最终预测结果。
通过这些方法,集成学习可以提高模型的预测性能、减少过拟合,并提高泛化能力。
1.2举例
假设我们有一个二分类问题,数据集包含以下数据:

我们将使用Bootstrap Aggregating(Bagging)方法结合3个决策树分类器(DT1,DT2,DT3)来解决这个问题。
对于每个基分类器,我们从原始数据集中随机抽样(有放回)一定数量的样本,形成新的训练集。例如,每个基分类器的训练集可能如下:
DT1 训练集: (1, 2, A), (2, 4, A), (3, 1, B), (3, 3, B)
DT2 训练集: (1, 4, A), (2, 4, A), (3, 3, B), (4, 2, B)
DT3 训练集: (1, 2, A), (1, 4, A), (3, 1, B), (4, 2, B)
使用这些新训练集分别训练3个决策树分类器。
对于新的未知数据点,例如(2, 3),我们使用这3个分类器进行预测,然后根据它们的输出进行投票:
DT1 预测:A
DT2 预测:A
DT3 预测:B
结果是类别 A 获得了2票,类别 B 获得了1票。因此,Bagging 预测该数据点属于类别 A。
通过这种方法,Bagging结合了多个基分类器的预测,降低了单个分类器的过拟合风险,并提高了整体模型的泛化能力。
2.设计思路以及代码
2.1设计思路
我们将使用scikit-learn库实现一个Bagging分类器。我们将:
(1)从scikit-learn库中导入所需的工具和数据集。
(2)实现一个Bagging分类器,其中基分类器为决策树。
(3)使用三个不同的数据集对分类器进行评估。
2.2代码实现
import numpy as np
from sklearn.datasets import load_iris, load_wine, load_breast_cancer
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载数据集
datasets = {
'Iris': load_iris(),
'Wine': load_wine(),
'Breast Cancer': load_breast_cancer()
}
# 初始化决策树和Bagging分类器
base_classifier = DecisionTreeClassifier()
bagging_classifier = BaggingClassifier(base_estimator=base_classifier, n_estimators=10, random_state=42)
# 评估Bagging分类器在不同数据集上的性能
results = {}
for dataset_name, dataset in datasets.items():
X_train, X_test, y_train, y_test = train_test_split(dataset.data, dataset.target, test_size=0.3, random_state=42)
bagging_classifier.fit(X_train, y_train)
y_pred = bagging_classifier.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
results[dataset_name] = accuracy
print("Bagging分类器在不同数据集上的准确率:")
for dataset_name, accuracy in results.items():
print(f"{dataset_name}: {accuracy:.4f}")
3.测试结果

根据测试结果,我们可以看到Bagging分类器在这三个数据集上的表现都非常好。这表明Bagging方法可以有效地减少过拟合,提高模型的泛化能力。
相关文章:

机器学习---集成学习报告
1.原理以及举例 1.1原理 集成学习(Ensemble Learning)是一种机器学习策略,它通过结合多个基学习器(base learners)的预测来提高模型的性能。集成学习的目标是创建一个比单个基学习器更准确、更稳定的最终预测模型。这…...
教你如何将PDF文件转换成PPT演示文稿
在工作和学习中,我们可能需要将一些PDF文件转换成PPT演示文稿,以便于更好地展示和分享。虽然PPT和PDF是两种不同的文档格式,但是我们可以使用一些专业的软件或在线工具来实现这种转换。下面就让我们来教你如何将PDF文件转换成PPT演示文稿。 …...

涨点技巧: 谷歌强势推出优化器Lion,引入到Yolov5/Yolov7,内存更小、效率更高,秒杀Adam(W)
1.Lion优化器介绍 论文:https://arxiv.org/abs/2302.06675 代码:automl/lion at master google/automl GitHub 1.1 简单、内存高效、运行速度更快 1)与 AdamW 和各种自适应优化器需要同时保存一阶和二阶矩相比,Lion 只需要动量,将额外的内存占用减半; 2)由于 Lion…...
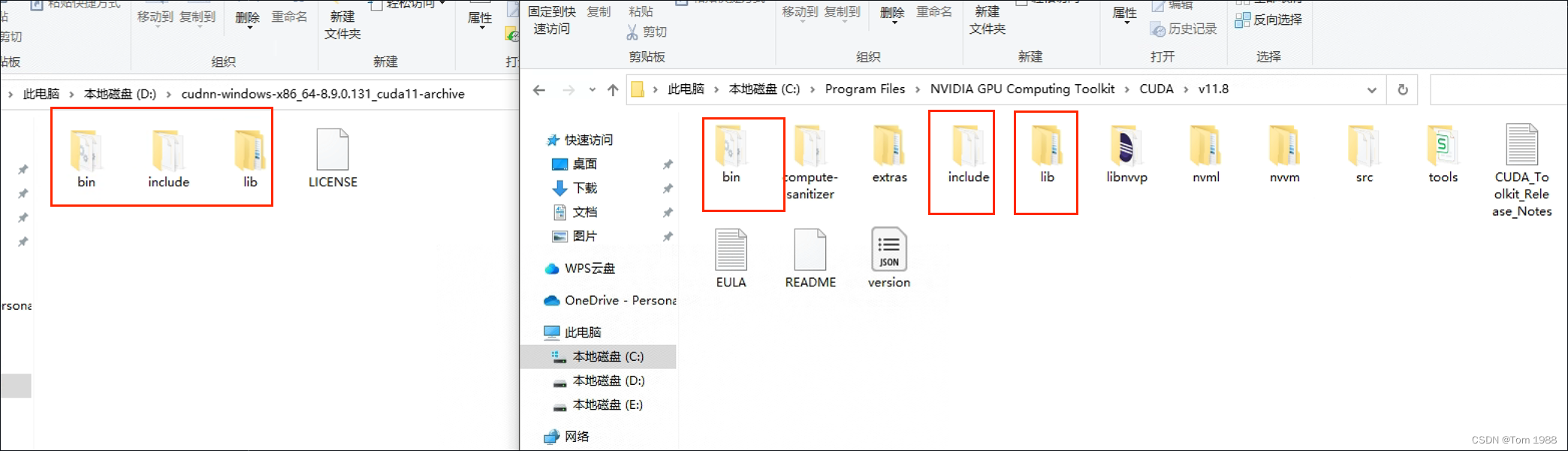
Windows GPU版本的深度学习环境安装
本文记录了cuda、cuDNN的安装配置。 参考文章: cuda-installation-guide-microsoft-windows 12.1 documentation Installation Guide :: NVIDIA cuDNN Documentation 一、cuda安装 注意事项: 1、cuda安装最重要的是查看自己应该安装的版本。 表格…...
C语言实践——通讯录(3)(文件版)
首先感谢上一篇博客的大佬们的点赞,非常感谢!!! 目录 前言 一、需要添加的功能 1.增加保存数据函数——可以保存数据到文件中 主要逻辑: 注意事项: 代码实现: 2.修改初始化函数——新…...

GPT撑腰,微软再战谷歌 | 大厂集体抢滩ChatGPT:谁真的有实力,谁在试点商业化?
国内互联网大厂已经很久没有这样的盛况了! 在各自领域成长为头部的互联网大厂们,近年来正在向“自留地”的纵深发展,正面交锋的机会并不多。直到大洋彼岸传来GPT的声音后,一下子抓住了大厂们的G点,他们仿佛听到了新一轮…...
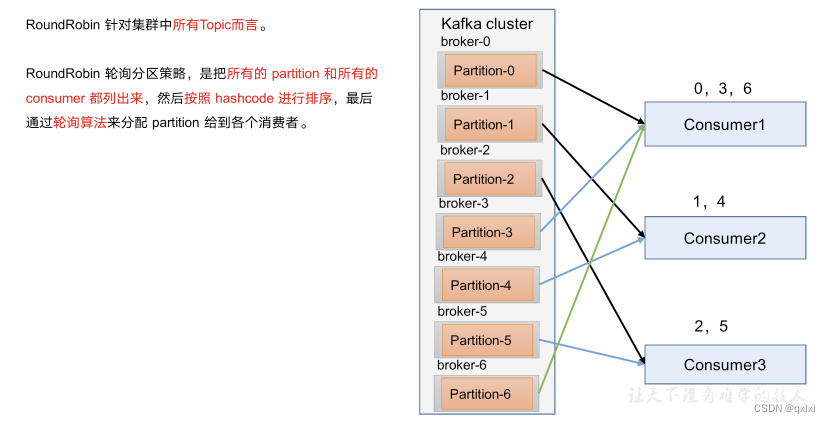
【消息队列】细说Kafka消费者的分区分配和重平衡
消费方式 我们直到在性能设计中异步模式,一般要么是采用pull,要么采用push。而两种方式各有优缺点。 pull :说白了就是通过消费端进行主动拉去数据,会根据自身系统处理能力去获取消息,上有Broker系统无需关注消费端的…...
——打印输出(详细语法参考 + 参数说明 + 具体示例)| 附:Python输出表情包)
【Python从入门到人工智能】14个必会的Python内置函数(7)——打印输出(详细语法参考 + 参数说明 + 具体示例)| 附:Python输出表情包
你仔细想想,你和谁在一起的时候,最放得开、最自然、最舒服,又毫无顾忌,可以做回真实的你。那个人才是你心里最特别,最重要的人。 🎯作者主页: 追光者♂🔥 🌸个人简介: 💖[1] 计算机专业硕士研究生💖 🌟[2] 2022年度博客之星人工智能领域TOP4�…...
为什么要创建FAQ?这篇文章告诉你
什么是FAQ 通过上述的引入大家应该也了解到了,FAQ是为了“解决问题”而存在的。FAQ是英文Frequently Asked Questions的缩写,中文意思就是“经常问到的问题”,或者更通俗地叫做“常见问题解答”。FAQ是当前网络上提供在线帮助的主要手段&…...

基于html+css的盒子展示1
准备项目 项目开发工具 Visual Studio Code 1.44.2 版本: 1.44.2 提交: ff915844119ce9485abfe8aa9076ec76b5300ddd 日期: 2020-04-16T16:36:23.138Z Electron: 7.1.11 Chrome: 78.0.3904.130 Node.js: 12.8.1 V8: 7.8.279.23-electron.0 OS: Windows_NT x64 10.0.19044 项目…...
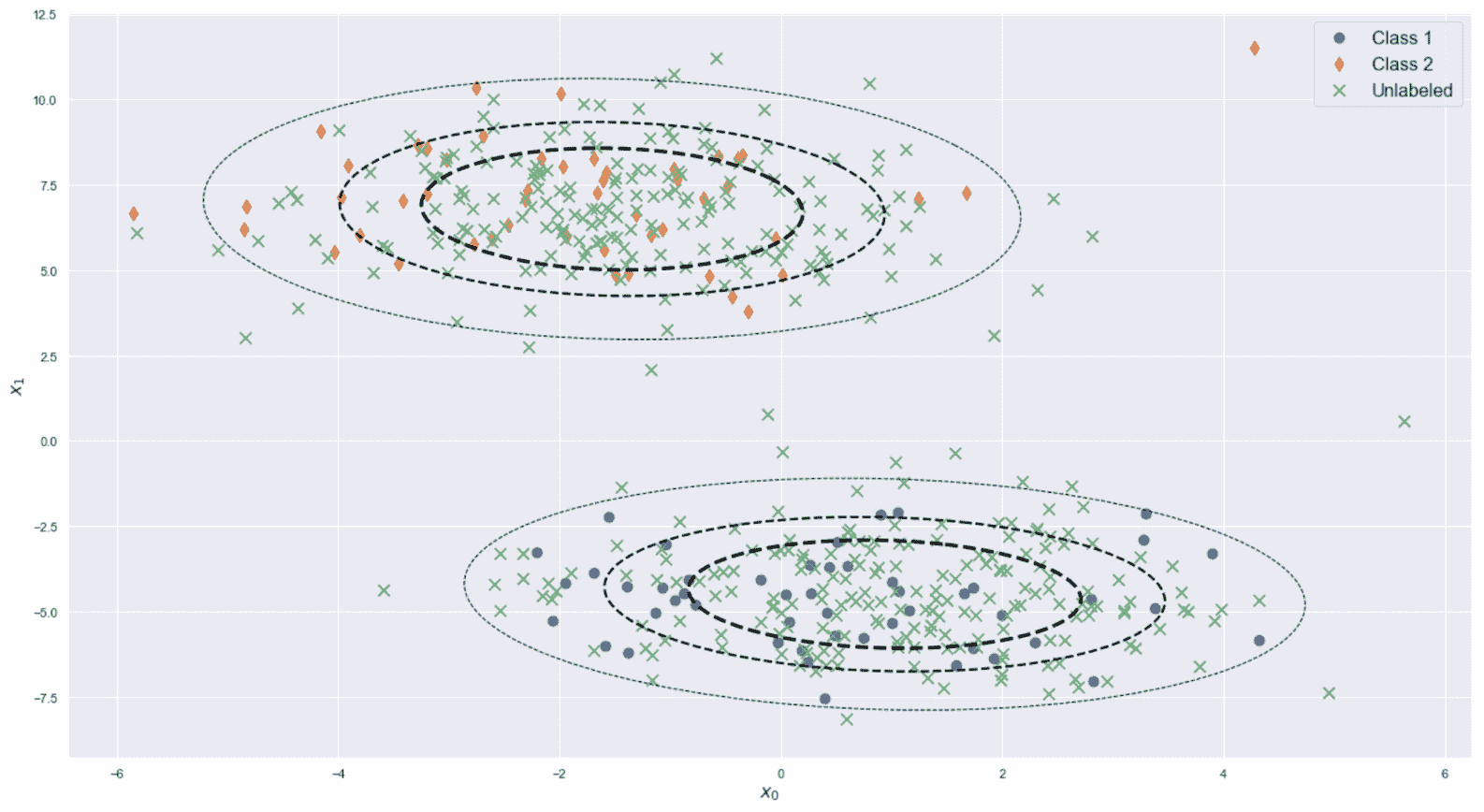
Python 无监督学习实用指南:1~5
原文:Hands-on unsupervised learning with Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关…...

2023 腾讯暑期实习申请经验分享
首先要向还在等我出 CMU 15-445 后面实验的同学们说声抱歉,这个系列可能暂时要停更啦。 一方面是博主最近课程和实验室方面的任务比较多,另一方面是有幸拿下了今年腾讯 WXG 后端开发的暑期实习 Offer,后面可能要提前学习一些工作中用到的框架…...

Protocol Buffers 介绍
Protocol Buffers Protocol Buffers ,协议缓冲区。什么是Protocol Buffers呢?或者我们简称PB 吧。那么Protocol Buffers 是一种与语言无关、与平台无关的可扩展机制,用于序列化结构化的数据。 example message Person {optional string nam…...

【模电实验】基尔霍夫定律、叠加定理和戴维南定理验证实验
实验目的 验证基尔霍夫电流定律(KCL)和电压定律(KVL)加深对该定理的理解验证叠加定理,加深对该定理的理解验证戴维南定理,掌握有源二端口网络的开路电压,短路电流和入端等效电阻的测定方法通过实…...

java某百货店POS积分管理系统_积分点更新生成以及通票回收处理
百货店是生活中不可缺少的一部分,为了给顾客提供更方便的服务平台以及更好的服务质量,而设计了POS积分管理系统。百货店通过点积分的管理获得顾客更好的信誉,增加客户流量,获得更多的利益。在百货店经营的过程中,每天的…...

Flutter 常用指令
1.flutter create app_01 :创建一个新的Flutter项目 2.flutter run:运行应用程序 3.flutter run -d <deviceId>:运行指定模拟器或者真机 4.flutter devices:查看计算机上的真机设备和IOS模拟器 5.flutter emulators&…...

定义全局变量property与getprop
authordaisy.skye的博客_CSDN博客-Qt,嵌入式,Linux领域博主 adb调试 adb shell getprop .adb logcat 报错 init: sys_prop: permission denied uid:1006 name:ro.camera.gc02m1 在linux驱动中查找 find ./ -name *.c | xargs grep -n "property_set" find ./ -n…...

双目三维测距(python)
文章目录 1. 双目检测1.1 调用相机1.2 分割画面 2. 双目标定2.1 相机标定2.2 获取参数 3. 双目测距3.1 立体校正3.1.1 校正目的3.1.2 校正方法3.1.2 相关代码 3.2 立体匹配和视差计算3.3 深度计算3.4 注意事项 4. 完整代码 代码打包下载: 链接1:https://…...

数据结构|二叉树的三种遍历方式,你掌握了几种?
目录 1、遍历方式 2、前序遍历 3、中序遍历 1、遍历方式 学习二叉树的结构,最简单的方式就是遍历二叉树。遍历二叉树就是通过某条线路对二叉树的各个结点进行一次访问,访问的方法有三种分为前序遍历、中序遍历、后续遍历,层序遍历它们的遍…...

Direct3D 12——灯光——法向量
a:平面法线着色 b:顶点法线着色 c:像素着色 平面法线(face normal,由于在计算机几何学中法线是有方向的向量,所以也有将normal译作法向量) 是 一种描述多边形朝向(即正交于多边形上所有点)的单位向量。 曲面法线&a…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
