Direct3D 12——灯光——法向量
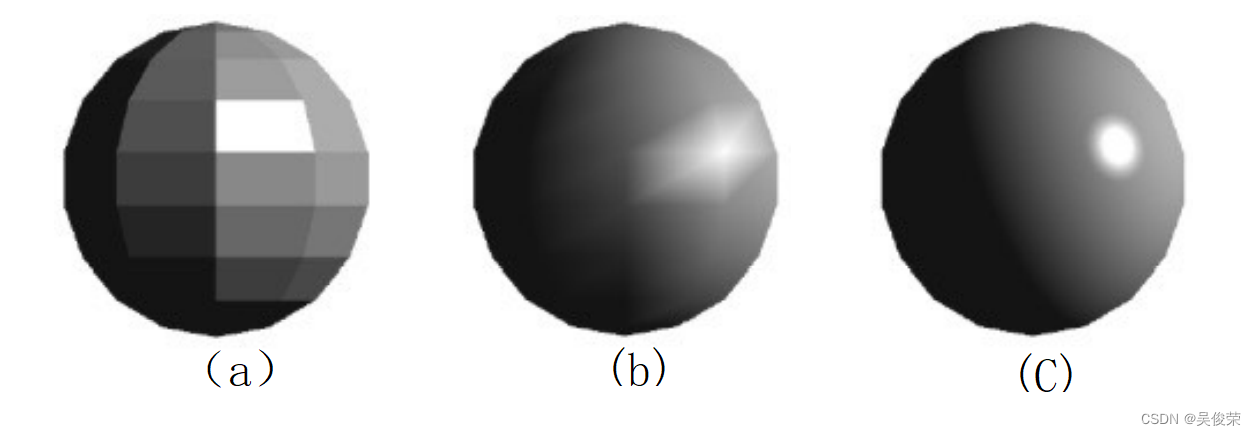
a:平面法线着色
b:顶点法线着色
c:像素着色
平面法线(face normal,由于在计算机几何学中法线是有方向的向量,所以也有将normal译作法向量)
是 一种描述多边形朝向(即正交于多边形上所有点)的单位向量。
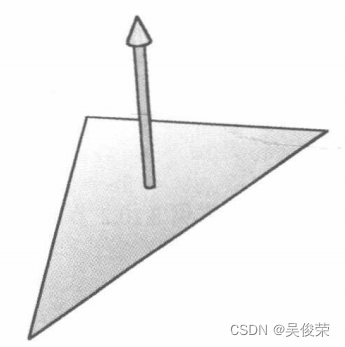
曲面法线(surface normal)
是 一种垂直于曲面上一点处切平面(有文献强调还要满足曲面发现经过该点这一条件件)的单位向量

对于光照计算来说,我们需要通过三角形网格曲面上每一点处的曲面法线来确定光线照到对应点上 的角度。为了求出曲面法线,我们仅先指定位于网格顶点处的曲面法线(所以也将之称作顶点法线,vertex normal )。接下来,为取得三角形网格曲面上每个点处的近似曲面法线,在三角形进行光栅化过程的中对 这些顶点法线进行插值计算
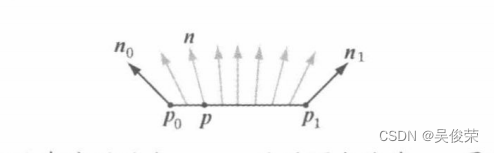
n0与n1分别是定义在线段端点p0、p1处的顶点法线。n是经此线段端点向量插值(加权平均值)所得到的点p处的法向量。即n=n0+t(n1-n0),这里的,满足p = p0+t(p1-p0)。
计算法向量
为了找到三角形Δp0p1p2的平面法线,我们首先计算位于三角形边上的两个向量:
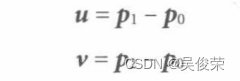 那么,此三角形的平面法线即为:
那么,此三角形的平面法线即为:
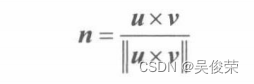
对于可微的光滑曲面而言,我们可以利用微积分方面的知识来 求出曲面点处的法线。但问题在于,三角形网格运用一种被称为求 顶点法线平均值(vertex normal averaging )的计算方法。此方法通过 对网格中共享顶点 v 的多边形的平面法线求取平均值,从而获得网 格中任意顶点 v 处的顶点法线n。例如,在图中,
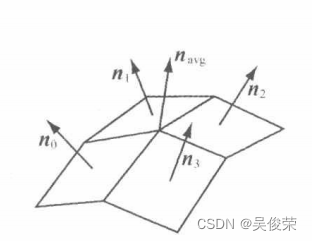
位于中间的顶点被四个多边形所共用,所以可通过计算这4个多边形平面法线的平均值来求取中间顶点处的近似法线
网格中的四个 多边形共用顶点v ,因此,v 处的顶点法线求法如下:
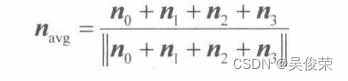
在上面这个例子中,由于我们对求和的结果已进行了规范化处 理,因此便无需像往常求算术平均值那样再除以4。注意,为了得 到更为精准的结果,我们还可以釆用更加复杂的求平均值方法,比如说,根据多边形的面积来确定权 重(如面积大的多边形的权重要大于面积小的多边形),以求取加权平均值。
变换法向量
思考图a。图中,切向量(tangent vector ) u=V1-V0 正交于法向量(normal vector ) n 。如果对此 应用一个非等比缩放变换A,则可从图b看到,变换后的切向量uA =v1A-V0A没能继续保持与变换 后法向量nA的正交性。
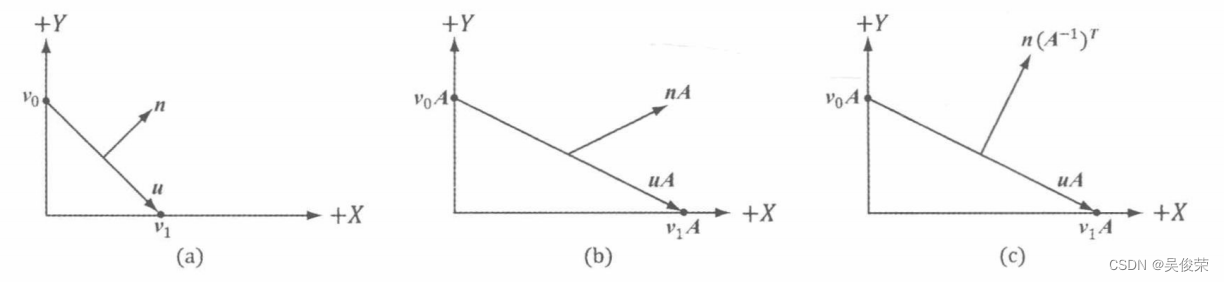
(a )切向量与法向量在变换前的正交关系
(b )经过在x轴正方向放大两倍的处理后,法向量
不再与切向量保持正交关系
(c)通过对法向量进行图b中缩放变换的逆转置矩阵运算后,法向量与切向量重归正交关系
所以,我们现在所面对的问题是,若给定一个用于变换点与向量(非法线)的变换矩阵A,如何能 够求出这样一个变换矩阵B:通过它来变换法向量,使经矩阵A变换后的切向量与法向量重归正交的关 系(即uA•nB=0 )。为此,我们首先从已知的信息着手,如果法向量n正交于切向量u则有:




尽管运用了逆转置变换,但法向量仍可能会失去其单位长度。所以在变换完成后,可能需 对它再次进行规范化处理。
相关文章:

Direct3D 12——灯光——法向量
a:平面法线着色 b:顶点法线着色 c:像素着色 平面法线(face normal,由于在计算机几何学中法线是有方向的向量,所以也有将normal译作法向量) 是 一种描述多边形朝向(即正交于多边形上所有点)的单位向量。 曲面法线&a…...
)
软考-信息系统工程(五)
信息系统工程 Garlan和Shaw对通用软件架构风格进行了分类,他们将软件架构分为:(曾经考过1分选择题 区分) 数据流风格:数据流风格包括批处理序列和管道/过滤器两种风格。调用/返回风格:调用/返回风格包括主程序/子程序、数据抽象和面向对象,以及层次结构…...
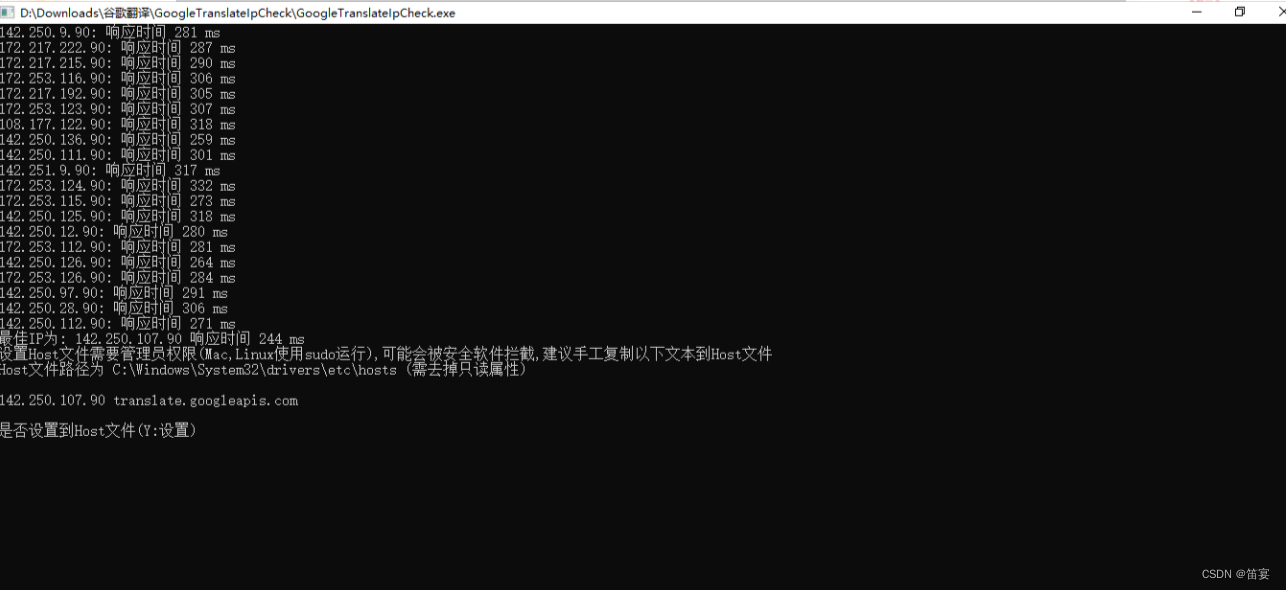
解决谷歌翻译不能使用的问题
今天登录国外网站,发现谷歌翻译已无法正常使用,网上最多的方法就是更改host文件,在host内增加ip地址,但是经常失效,经常手动更改增加ip着实烦恼,还有可能有别的错误。 最终解决方式是:登录GitH…...
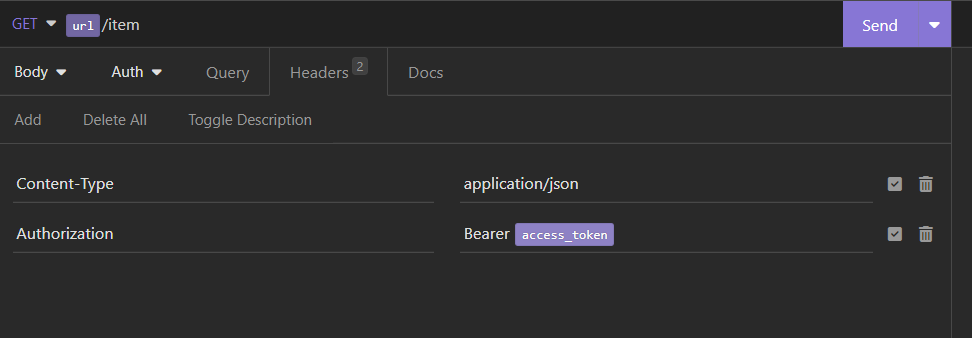
Insomnia 简单使用方法
文章目录 1. 新建工程2. 新建若干文件夹3. 设置环境变量4. 授权以及进行请求的链式调用 (chaining requests)4. 1 解决办法 14. 2 解决办法 2 Insomnia 同 Postman, 用于测试后端 endpoint,很容易使用。 使用步骤如下: 1. 新建工程 2. 新建若…...

2023接口自动化测试,完整入门篇
1. 什么是接口测试 顾名思义,接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程,以及相互逻辑依赖关系。其中接口协议分为HTTP,WebService,Dubbo,Thrift,Socket等类型,测试类型又主…...
2023年股票代持行业研究报告
第一章 股票代持概述 1.1 基本概念 股票代持,或称委托持股,是指实际出资人与名义出资人达成以下约定:名义出资人作为名义股东,在股东名册等公司工商登记信息上出现,而实际上由实际出资人出资并享有投资权益。 股票代…...
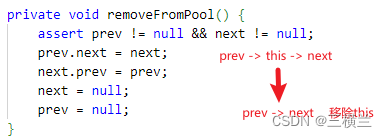
《Netty》从零开始学netty源码(三十九)之PoolSubPage的内存分配
目录 PoolSubPage.allocategetNextAvail方法toHandle方法removeFromPool方法 PoolSubPage.allocate 上一篇我们介绍了PoolSubPage的简单知识,当我们需要PoolSubPage的内存时可调用allocate方法查找可分配二进制的位置,具体的源码过程如下: …...

【目标检测论文阅读笔记】Reducing Label Noise in Anchor-Free Object Detection
(Augmentation for small object detection) Abstract 当前的 anchor-free无锚目标检测器 将空间上落在真值框预定义中心区域内的所有特征标记为正。这种方法会在训练过程中产生 标签噪声,因为这些 正标记的特征中的一些 可能位于背景或遮挡…...

金融数字新型基础设施创新开放联合体今日成立
4月18日,“金融数字新型基础设施创新开放联合体”(以下简称:联合体)在上海成立。联合体由上海银行、复旦大学金融科技研究院、中电金信共同发起,首批成员单位汇聚产业链与供给侧的中坚力量:国泰君安证券、太…...

编程语言的发展史
编程语言处在不断的发展和变化中,从最初的机器语言发展到如今的2500种以上的高级语言,每种语言都有其特定的用途和不同的发展轨迹。编程语言并不像人类自然语言发展变化一样的缓慢而又持久,其发展是相当快速的,这主要是计算机硬件…...

巧用千寻位置GNSS软件|点测量采集技巧
点测量是测量中重要的节点,在测量工作的信息处理分析中发挥着重要作用。本期将给各位带来使用千寻位置GNSS软件采集地形点、控制点、快速点、连续点、房角点和倾斜点的操作技巧。 地形点 地形点的设置如图 5.1-9所 示,每次采集一个点,该点需要…...
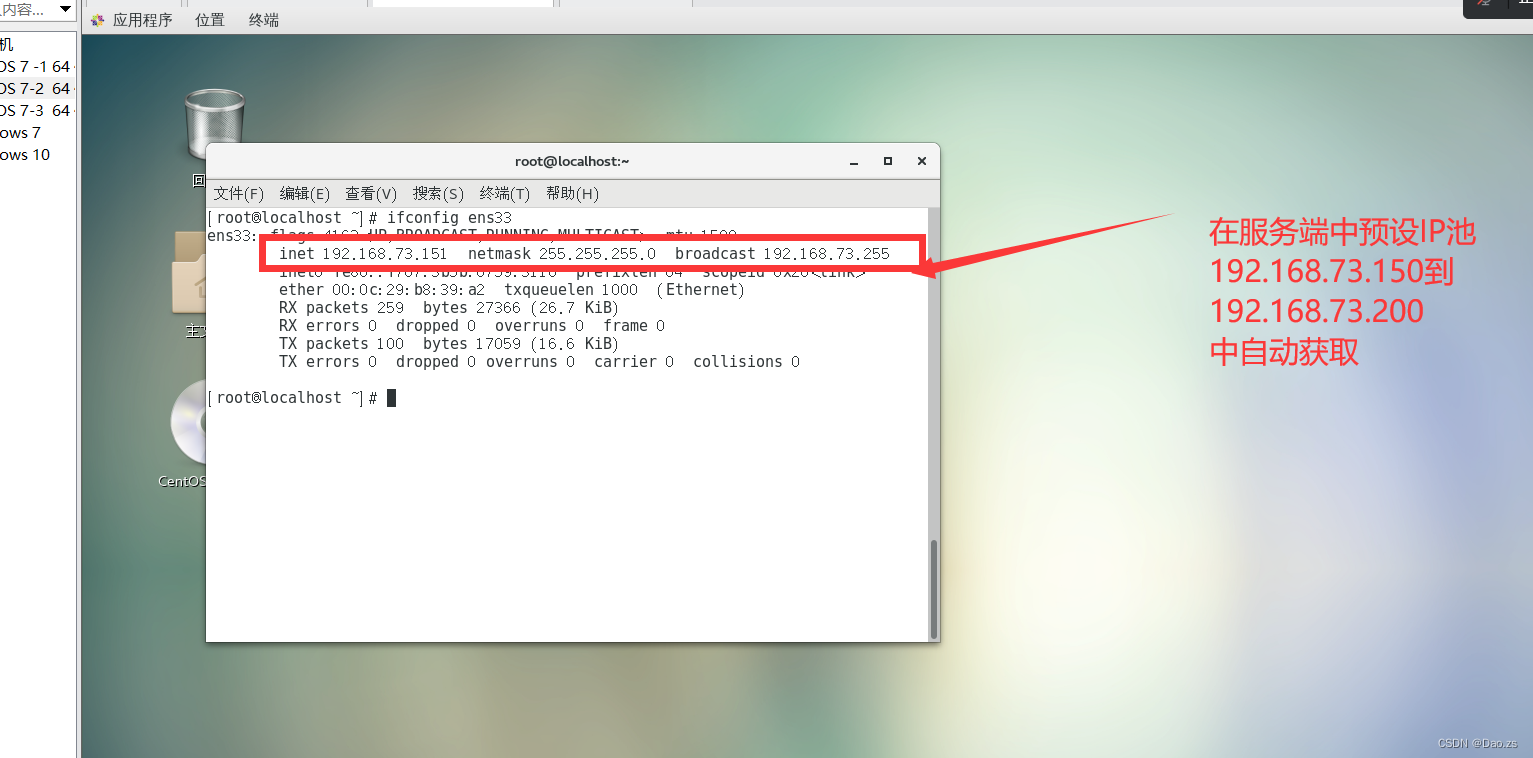
DHCP原理与配置
目录 一、DHCP工作原理 1)了解DHCP服务 使用DHCP的好处 DHCP的分配方式 2)DHCP的租约过程 分为四个步骤 二、DHCP服务器的配置 1)检查并且安装dhcp有关软件包 2)查看系统的配置文件,并且利用好官方给的参考案…...

软件测试今天你被内卷了吗?
认识一个人,大专学历非计算机专业的,是前几年环境好的时候入的行,那时候软件测试的要求真的很低,他那时好像是报了个班,然后入门的,但学的都是些基础,当时的他想的也简单,反正也能拿…...

做完自动化测试,但别让不会汇报毁了你...
pytest 是一个成熟的全功能Python测试工具,可以帮助您编写更好的程序。它与 python 自带的 unittest 测试框架类似,但 pytest 使用起来更简洁和高效,并且兼容 unittest 框架。pytest 能够支持简单的单元测试和复杂的功能测试,pyte…...
企业级信息系统开发讲课笔记2.4 利用MyBatis实现条件查询
文章目录 零、本节学习目标一、查询需求二、打开MyBatisDemo项目三、对学生表实现条件查询(一)创建学生映射器配置文件(二)配置学生映射器文件(三)创建学生映射器接口(四)测试学生映…...
)
【天梯赛—不想坑队友系列】L2-003 月饼(java)
目录 第一题: L2-003 月饼 输入格式: 输出格式: 输入样例: 输出样例: 题目分析 题目代码 第二题:德才论 输入格式: 输出格式: 输入样例: 输出样例ÿ…...
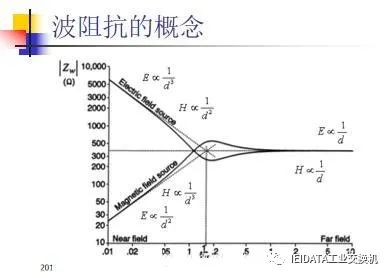
电磁兼容(EMC)的标准与测试内容
在国际范围上,电磁兼容标准的制定已经有了70多年的发展历程,最早为了保护无线电通信和广播,国际无线电干扰特别委员会(CISPR)对各种用电设备和系统提出了相关的电磁干扰发射限值和测量方法。到了20世纪60~7…...

滑动平均算法
class Solution { public static int[] maxSlidingWindow(int[] nums, int k) { int right 0; int[] res new int[nums.length -k 1]; int index0; LinkedList<Integer> list new LinkedList<>(); // 开始构造窗口 …...

个人职业发展
职业的本质就是人和社会的交换关系。选择什么职业,等于选择了用什么方式和世界交换。 比如,快递员、小时工靠“体力”;大多数打工者靠“体力智力”;网红靠“资源、平台”;各领域的大神、科学家、艺术家靠“天赋”。 这…...
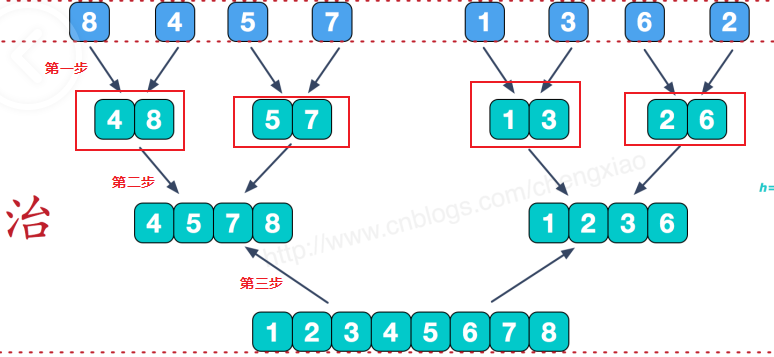
剑指 Offer 51. 数组中的逆序对
剑指 Offer 51. 数组中的逆序对 难度:hard\color{red}{hard}hard 题目描述 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。 示例 1: 输入: [7…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
