【模电实验】基尔霍夫定律、叠加定理和戴维南定理验证实验
- 实验目的
- 验证基尔霍夫电流定律(KCL)和电压定律(KVL)加深对该定理的理解
- 验证叠加定理,加深对该定理的理解
- 验证戴维南定理,掌握有源二端口网络的开路电压,短路电流和入端等效电阻的测定方法
- 通过实验加强对参考方向的掌握和运用的能力
- 实验原理与说明
1.叠加定理:
对于一个具有唯一解的线性电路,由几个独立电源共同作用所形成的各支路电流或电压,是各个独立电源分别单独作用时在各相应支路中形成的电流或电压的叠加。

图1-1所示实验电路中有一个电压源Us及一个电流源Is。 设Us和Is共同作用在电阻RL、R3上产生的电流分别为IAB、IDB,如图1-1(a)所示。为了验证叠加原理令电压源和电流源分别作用。当电压源Us不作用,即Us=0时,在Us处用短路线代替;当电流源Is不作用,即Is=0时,在Is处用开路代替;而电源内阻都必须保留在电路中。
- 设电压源Us单独作用时(电流源支路开路)在电阻RL、R3上产生的电流分别为IAB‘、IDB‘
 ,如图1-1(b)所示。
,如图1-1(b)所示。 - 设电流源单独作用时(电压源支路短路)在电阻RL、R3上产生的电流分别为IAB‘’、IDB‘’
 ,如图1-1(c)所示。
,如图1-1(c)所示。
这些电流的参考方向均已在图中标明。验证叠加定理,即验证式(1-1)成立。 IAB![]() = IAB‘+ IAB‘’
= IAB‘+ IAB‘’![]()
IDB![]() = IDB ‘+ IDB‘’
= IDB ‘+ IDB‘’![]() 式(1-1)
式(1-1)
2.基尔霍夫定律
1)基尔霍夫电流定律(KCL)
在任一时刻,流出(或流入)集中参数电路中任一节点的电流的代数和恒等于零,即: ΣI=0 或 ΣI入=ΣI出 式(1-2)
此时,若取流出节点的电流为正,则流入节点的电流为负。它反映了电流的连续性。说明了节点上各支路电流的约束关系,它与电路中元件的性质无关。
图1-1所示实验电路中要验证基尔霍夫电流定律,可选一电路节点B,按图中电流的参考方向测定出各支路电流值,并约定流出该节点的电流为正,反之取负号。将测得的各电流代入式(1-2),即:IS-IAB-IDB=0或IS=IAB+IDB加以验证。
2)基尔霍夫电压定律(KVL)
按约定的参考方向,在任一时刻,集中参数电路中任一回路上全部元件两端电压代数和恒等于零,即:ΣU=0 式(1-3)
它说明了电路中各段电压的约束关系,它与电路中元件的性质无关。式(1-3)中,通常规定凡支路或元件电压的参考方向与回路绕行方向一致者取正号,反之取负号。
图1-1所示实验电路中要验证基尔霍夫电压定律,可选电路右边回路,回路绕行方向为顺时针,按图中的参考方向测定出回路中各元件电压值,并约定与回路绕行方向一致者取正号,反之取负号,将测得的各电压代入式(1-3),,即:UAB+UBC+UCA=0加以验证。
3.电压、电流的实际方向与参考方向的对应关系
参考方向是为了分析、计算电路而人为设定的,如下图1-2所示。实验中测量的电压、电流的实际方向,由电压表、电流表的“正”端所标明。在测量电压、电流时,若电压表、电流表的“正”端与参考方向的“正”方向一致,则该测量值为正值,否则为负值。

4.戴维南定理
一个含独立电源,受控源和线性电阻的二端口网络,其对外作用可以用一个电压源串联电阻的等效电源代替,其等效源电压等于此二端口网络的开路电压,其等效内阻是二端口网络内部各独立电源置零后所对应的不含独立源的二端口网络的输入电阻(或称等效电阻)如图1-3所示。
5. 诺顿定理
一个含独立电源,受控源和线性电阻的二端口网络,其对外作用可以用一个电流源并联电阻的等效电源代替,其等效源电流等于此二端口网络的短路电流,其等效内阻是二端口网络内部各独立电源置零后所对应的不含独立源的二端口网络的输入电阻(或称等效电阻)如图1-4所示。

6. 有源二端网络等效参数的测量方法-----开路电压、短路电流法:
在有源二端网络输出端开路时,用电压表直接测量其输出端的开路电压Uoc,然后将输出端短路,用电流表测量其短路电流Isc,则等效电阻为
![]()
- 实验设备
名称 数量 型号
- 双路可调直流电源 1块 30121046
- 直流电压电流表 1块 30111047
- 电阻 4只 10W*1 330W*1 510W*2
- 测电流插孔 3只
- 电流插孔导线 3条
- 短接桥和连接导线 若干 P8-1和50148
- 实验用9孔插件方板 1块 300mm×298mm
- 可调电阻 1只 1000W*1
- 实验步骤
1. 实验电路如下图1-5所示,其中R1=330欧,R2= R3=510欧, R4=10欧, RL=400欧,稳压源的输出Es=12V,恒流源的输出Is=10mA。注意:应将稳压源调出相应的值再接入电路。恒流源接入电路中再调出相应的值。
分以下3种情况分别测量 Uab ,Ubc , Uca, Iab, Idb。将结果填入下表, 注意每次测量,读取数据时各支路电流及支路电压取关联参考方向。
1)令电压源、电流源共同作用。
2)令电压源单独作用。
3)令电流源单独作用

a.叠加原理的验证
根据表1-1测量的数据,通过计算分别验证Uab ,Ubc , Uca, Iab, Idb的值满足下面的叠加原理公式:
Y电压源、电流源共同作用=Y电压源单独作用+Y电流源单独作用
b. 基尔霍夫定律的验证
1)根据表1-1测量的数据,通过计算验证节点B的KCL方程: ΣI=0
2)根据表1-1测量的数据,通过计算验证回路ABC的KVL方程: ΣU=0

2. 戴维南、诺顿定理的验证
验证戴维南、诺顿定理的一个有源二端网络,如下图1-6(a)中虚线所示,其中R1=330欧,R2= R3=510欧, R4=10欧,用开路电压、短路电流法,测量该有源二端网络的开路电压Uoc和短路电流Isc,并计算R0,数据记录于表2中

(1)测量有源二端网络的外特性
在图1-6(a)所示电路中接入负载电阻RL(RL是由可变电阻组成的,使用前要先找准其零位,即RL=0的位置),改变RL的值,测量其两端电压和通过的电流,数据记录于表3中。
表3
| RL(Ω) | 0 | 200 | 400 | 600 | 800 | 1000 | ∞ |
| U(V) | |||||||
| I(mA) |
(2)测量戴维南等效电路的外特性
构成戴维南等效电路如图1-6(b)所示(图中电压源Uoc和内阻R0为表2中测得的值,根据内阻R0的大小用实验箱中的510Ω、1Ω、2.2Ω、5.1Ω,10Ω等电阻串联在一起尽量接近R0的值(要求误差小于1Ω),;负载电阻RL仍用可变电阻器,改变RL的值,测量其两端电压和通过的电流,数据记录于表4中。
表4
| RL(Ω) | 0 | 200 | 400 | 600 | 800 | 1000 | ∞ |
| U(V) | |||||||
| I(mA) |
(3) 测量诺顿等效电路的外特性
构成诺顿等效电路如图1-4(b)所示,图中电压源Isc和等效电阻R0为表2中测得的值,根据等效电阻Ro的大小用实验箱中的510Ω、1Ω、2.2Ω、5.1Ω,10Ω等电阻串联在一起, 尽量接近Ro的值(要求误差小于1Ω);负载电阻RL仍用可变电阻器),改变RL的值,测量其两端电压和通过的电流,数据记录于表5中。
表5
| RL(Ω) | 0 | 200 | 400 | 600 | 800 | 1000 | ∞ |
| U(V) | |||||||
| I(mA) |
- 注意事项
- 测量电压、电位、电流时,不但要读出数值来,还要判断实际方向,并与设定的参考方向进行比较,若不一致,则该数前加“-”号。
- 注意稳压电源的输出端切勿短路,恒流源不可开路。
- 换接线路时,必须先关断电源。
- 实验完毕,须将导线、仪表归位,恢复到待使用状态。
- 分析和讨论
- 测量电压、电流时,如何判断数据前的正负号?负号的意义是什么?
- 电位出现负值,其意义是什么?
- 叠加原理、基尔霍夫定律和戴维南、诺顿定律分别在什么条件下成立?
- 在实验中,处理电压源和电流源的具体步骤和注意事项是什么?为什么?
- 实验报告要求
1.根据表1-1的测量数据,通过计算验证叠加定理和基尔霍夫定律的正确性。
2.电阻元件所消耗的功率能否用叠加原理计算而得,用实验数据通过计算结果说明。
3.根据表3、4、5的测量数据,在同一坐标纸上绘出各自的伏安特性曲线,比较其结果,以验证戴维南、诺顿定理及其等效变换的正确性。
4. 分析实验误差,总结实验收获和体会。
实验数据(仅供参考)





相关文章:

【模电实验】基尔霍夫定律、叠加定理和戴维南定理验证实验
实验目的 验证基尔霍夫电流定律(KCL)和电压定律(KVL)加深对该定理的理解验证叠加定理,加深对该定理的理解验证戴维南定理,掌握有源二端口网络的开路电压,短路电流和入端等效电阻的测定方法通过实…...

java某百货店POS积分管理系统_积分点更新生成以及通票回收处理
百货店是生活中不可缺少的一部分,为了给顾客提供更方便的服务平台以及更好的服务质量,而设计了POS积分管理系统。百货店通过点积分的管理获得顾客更好的信誉,增加客户流量,获得更多的利益。在百货店经营的过程中,每天的…...

Flutter 常用指令
1.flutter create app_01 :创建一个新的Flutter项目 2.flutter run:运行应用程序 3.flutter run -d <deviceId>:运行指定模拟器或者真机 4.flutter devices:查看计算机上的真机设备和IOS模拟器 5.flutter emulators&…...

定义全局变量property与getprop
authordaisy.skye的博客_CSDN博客-Qt,嵌入式,Linux领域博主 adb调试 adb shell getprop .adb logcat 报错 init: sys_prop: permission denied uid:1006 name:ro.camera.gc02m1 在linux驱动中查找 find ./ -name *.c | xargs grep -n "property_set" find ./ -n…...

双目三维测距(python)
文章目录 1. 双目检测1.1 调用相机1.2 分割画面 2. 双目标定2.1 相机标定2.2 获取参数 3. 双目测距3.1 立体校正3.1.1 校正目的3.1.2 校正方法3.1.2 相关代码 3.2 立体匹配和视差计算3.3 深度计算3.4 注意事项 4. 完整代码 代码打包下载: 链接1:https://…...

数据结构|二叉树的三种遍历方式,你掌握了几种?
目录 1、遍历方式 2、前序遍历 3、中序遍历 1、遍历方式 学习二叉树的结构,最简单的方式就是遍历二叉树。遍历二叉树就是通过某条线路对二叉树的各个结点进行一次访问,访问的方法有三种分为前序遍历、中序遍历、后续遍历,层序遍历它们的遍…...

Direct3D 12——灯光——法向量
a:平面法线着色 b:顶点法线着色 c:像素着色 平面法线(face normal,由于在计算机几何学中法线是有方向的向量,所以也有将normal译作法向量) 是 一种描述多边形朝向(即正交于多边形上所有点)的单位向量。 曲面法线&a…...
)
软考-信息系统工程(五)
信息系统工程 Garlan和Shaw对通用软件架构风格进行了分类,他们将软件架构分为:(曾经考过1分选择题 区分) 数据流风格:数据流风格包括批处理序列和管道/过滤器两种风格。调用/返回风格:调用/返回风格包括主程序/子程序、数据抽象和面向对象,以及层次结构…...
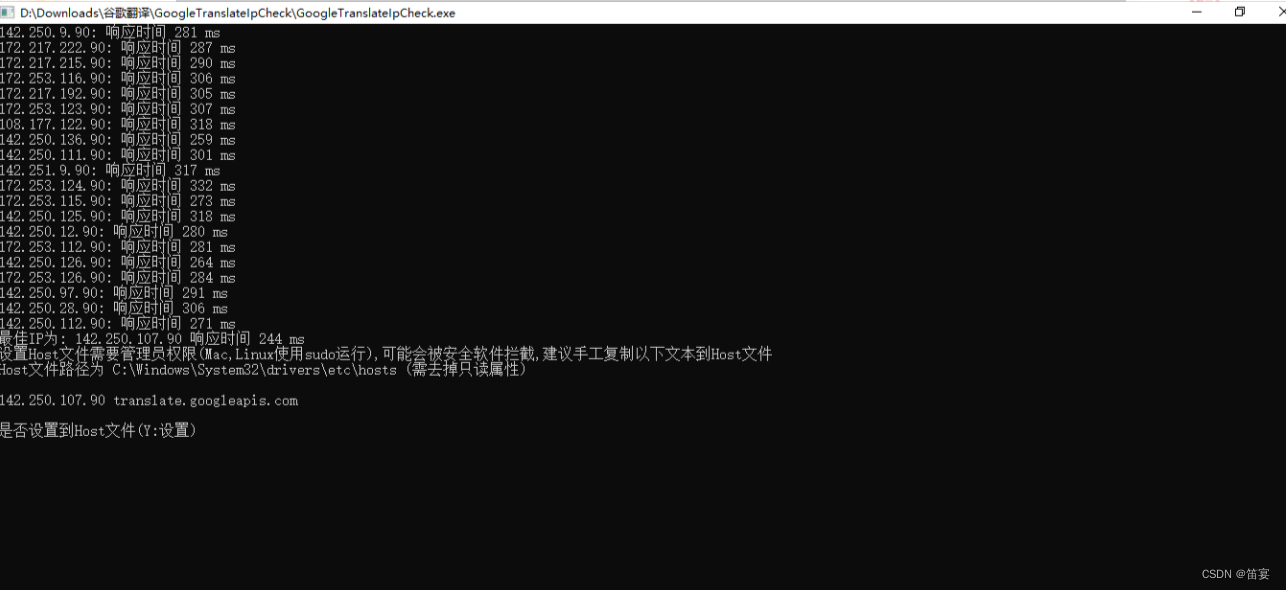
解决谷歌翻译不能使用的问题
今天登录国外网站,发现谷歌翻译已无法正常使用,网上最多的方法就是更改host文件,在host内增加ip地址,但是经常失效,经常手动更改增加ip着实烦恼,还有可能有别的错误。 最终解决方式是:登录GitH…...
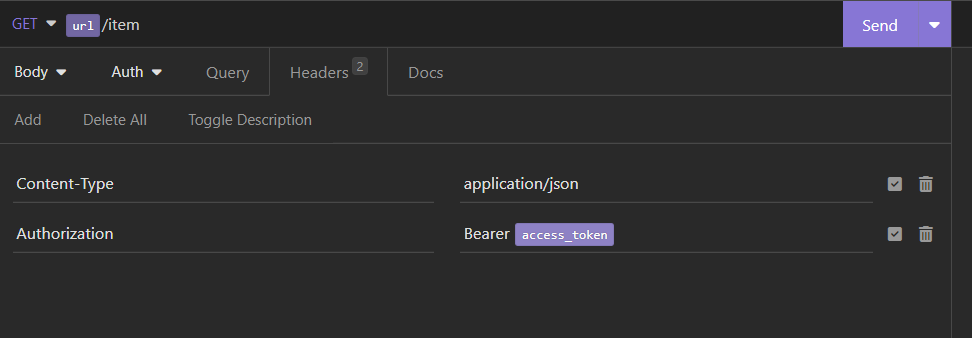
Insomnia 简单使用方法
文章目录 1. 新建工程2. 新建若干文件夹3. 设置环境变量4. 授权以及进行请求的链式调用 (chaining requests)4. 1 解决办法 14. 2 解决办法 2 Insomnia 同 Postman, 用于测试后端 endpoint,很容易使用。 使用步骤如下: 1. 新建工程 2. 新建若…...

2023接口自动化测试,完整入门篇
1. 什么是接口测试 顾名思义,接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程,以及相互逻辑依赖关系。其中接口协议分为HTTP,WebService,Dubbo,Thrift,Socket等类型,测试类型又主…...
2023年股票代持行业研究报告
第一章 股票代持概述 1.1 基本概念 股票代持,或称委托持股,是指实际出资人与名义出资人达成以下约定:名义出资人作为名义股东,在股东名册等公司工商登记信息上出现,而实际上由实际出资人出资并享有投资权益。 股票代…...
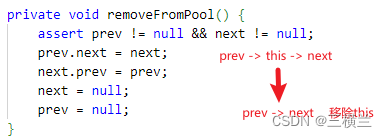
《Netty》从零开始学netty源码(三十九)之PoolSubPage的内存分配
目录 PoolSubPage.allocategetNextAvail方法toHandle方法removeFromPool方法 PoolSubPage.allocate 上一篇我们介绍了PoolSubPage的简单知识,当我们需要PoolSubPage的内存时可调用allocate方法查找可分配二进制的位置,具体的源码过程如下: …...

【目标检测论文阅读笔记】Reducing Label Noise in Anchor-Free Object Detection
(Augmentation for small object detection) Abstract 当前的 anchor-free无锚目标检测器 将空间上落在真值框预定义中心区域内的所有特征标记为正。这种方法会在训练过程中产生 标签噪声,因为这些 正标记的特征中的一些 可能位于背景或遮挡…...

金融数字新型基础设施创新开放联合体今日成立
4月18日,“金融数字新型基础设施创新开放联合体”(以下简称:联合体)在上海成立。联合体由上海银行、复旦大学金融科技研究院、中电金信共同发起,首批成员单位汇聚产业链与供给侧的中坚力量:国泰君安证券、太…...

编程语言的发展史
编程语言处在不断的发展和变化中,从最初的机器语言发展到如今的2500种以上的高级语言,每种语言都有其特定的用途和不同的发展轨迹。编程语言并不像人类自然语言发展变化一样的缓慢而又持久,其发展是相当快速的,这主要是计算机硬件…...

巧用千寻位置GNSS软件|点测量采集技巧
点测量是测量中重要的节点,在测量工作的信息处理分析中发挥着重要作用。本期将给各位带来使用千寻位置GNSS软件采集地形点、控制点、快速点、连续点、房角点和倾斜点的操作技巧。 地形点 地形点的设置如图 5.1-9所 示,每次采集一个点,该点需要…...
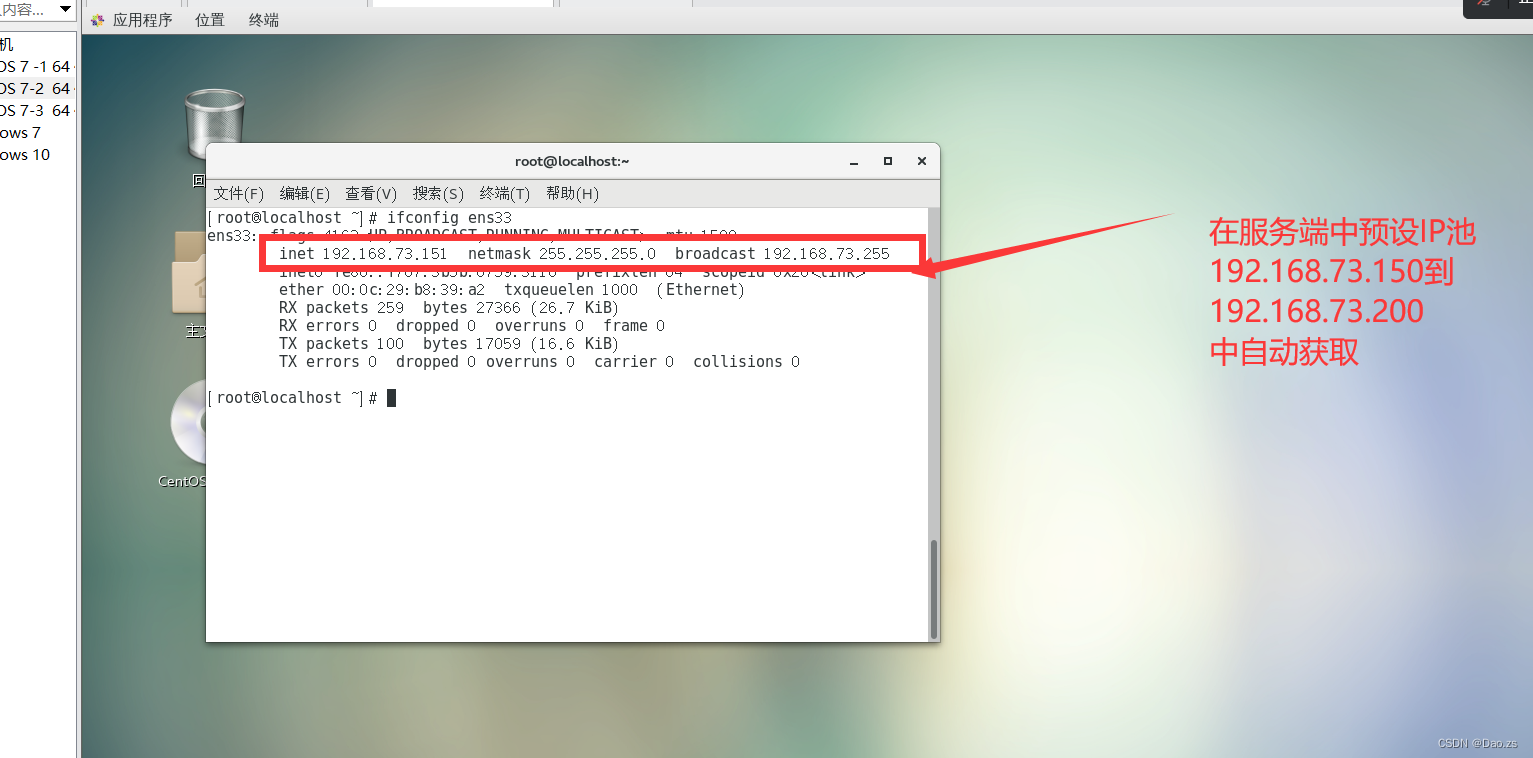
DHCP原理与配置
目录 一、DHCP工作原理 1)了解DHCP服务 使用DHCP的好处 DHCP的分配方式 2)DHCP的租约过程 分为四个步骤 二、DHCP服务器的配置 1)检查并且安装dhcp有关软件包 2)查看系统的配置文件,并且利用好官方给的参考案…...

软件测试今天你被内卷了吗?
认识一个人,大专学历非计算机专业的,是前几年环境好的时候入的行,那时候软件测试的要求真的很低,他那时好像是报了个班,然后入门的,但学的都是些基础,当时的他想的也简单,反正也能拿…...

做完自动化测试,但别让不会汇报毁了你...
pytest 是一个成熟的全功能Python测试工具,可以帮助您编写更好的程序。它与 python 自带的 unittest 测试框架类似,但 pytest 使用起来更简洁和高效,并且兼容 unittest 框架。pytest 能够支持简单的单元测试和复杂的功能测试,pyte…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
