数据结构|二叉树的三种遍历方式,你掌握了几种?

目录
1、遍历方式
2、前序遍历
3、中序遍历

1、遍历方式
学习二叉树的结构,最简单的方式就是遍历二叉树。遍历二叉树就是通过某条线路对二叉树的各个结点进行一次访问,访问的方法有三种分为前序遍历、中序遍历、后续遍历,层序遍历它们的遍历顺序如下所示:
- 前序遍历:根节点=》根节点的左子树=》根节点的右子树
- 中序遍历:根节点的左节点=》根节点=》根节点的右子树
- 后续遍历:根节点的左节点=》根节点的右节点=》根节点
在二叉树的遍历中,遍历的开始是从头节点开始的遍历的结束也是从头节点结束的。
有一个二叉树,它有六个节点ABCDEF其值为123456。对应的结构为:
- A为根节点时,A的左子树是D,A的右子树是E,A的值为1。
- B为根节点时,B的左子树是D,B的右子树是E,B的值为2。
- C为根节点时,C的左子树是null,C的右子树是F,C的值为3。
- D为根节点时,D的左子树是null,F的右子树是null,的值为4。
- E为根节点时,E的左子树是null,F的右子树是null,的值为5。
- F为根节点时,F的左子树是null,F的右子树是null,的值为6。
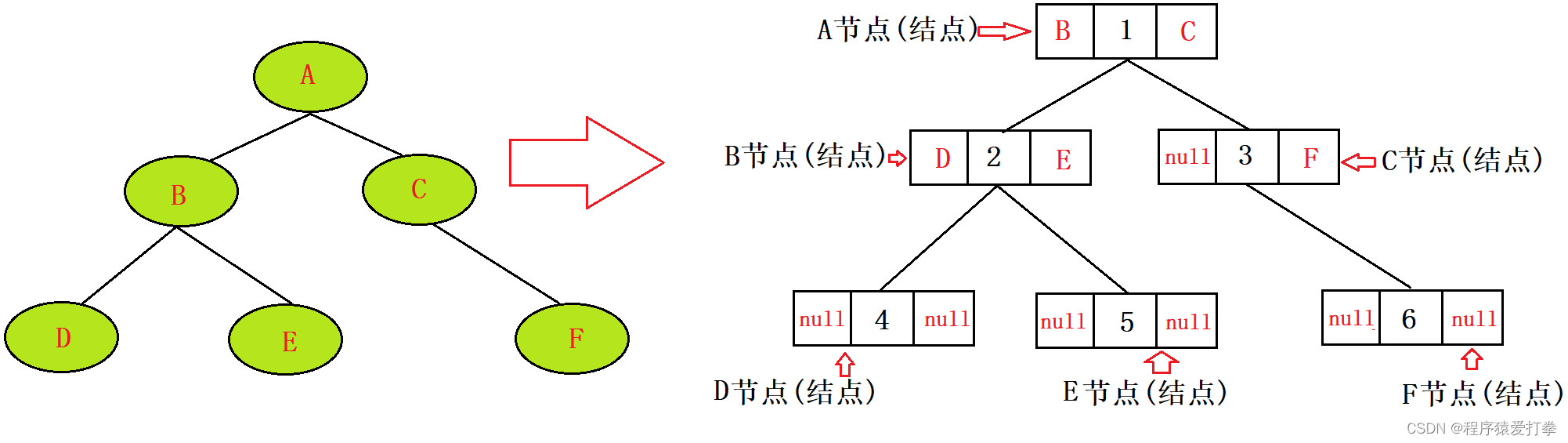
本期博文所演练的遍历方式,均以上图中的二叉树进行展示。
2、前序遍历
前序遍历,我们在上方已经了解到了它的遍历顺序为:根节点=》根节点的左子树=》根节点的右子树。因此前序遍历上述的定义好的二叉树的顺序应为:ABDECF得到的值也应该为124536。具体实现方式看下方讲解:
第一步,获取根节点A。判断A节点是否有左子树。有则往下一个左子树遍历。没有则遍历右子树,右子树也没有则返回父节点。如果无父节点则程序结束!
此步骤往A的左子树进行遍历,首先获取A节点,发现A存在左子树,则往下遍历A的左子树节点。此时遍历到节点为:A、元素为:1。
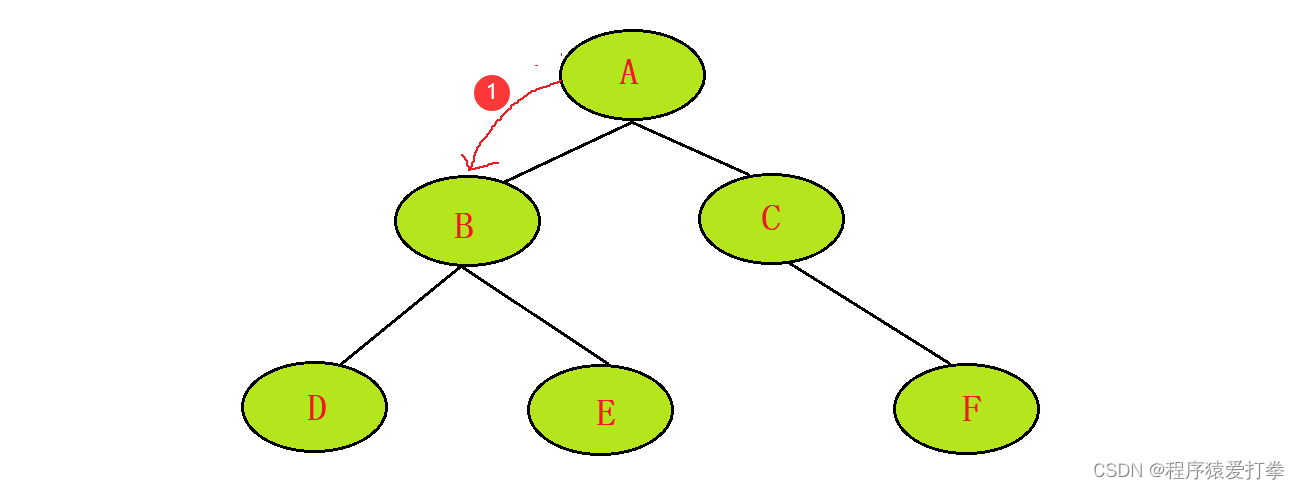
第二步,来到B节点,获取B节点。判断B节点是否有左子树。有则往下一个左子树遍历。没有则遍历右子树,右子树也没有则返回父节点。如果无父节点则程序结束!
此步骤往B的左子树进行遍历,发现B存在左子树,则往下遍历B的左子树节点。此时遍历到的节点为AB、元素为:12。
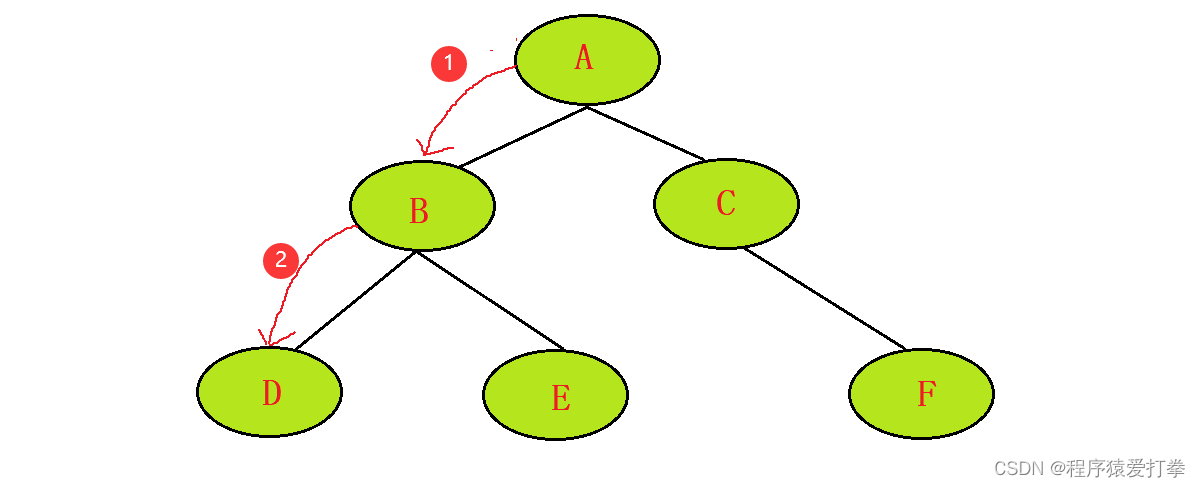
第三步,来到D节点,获取D节点。然后判断D节点是否有左子树有则往下一个节点遍历。没有则遍历右子树,右子树也没有则返回父节点。
此时发现D没有左子树,遍历D的右子树发现右子树也没有,返回到B节点,并且往B节点的右子树进行遍历。 此时遍历到的节点为:ABD、元素为:124。
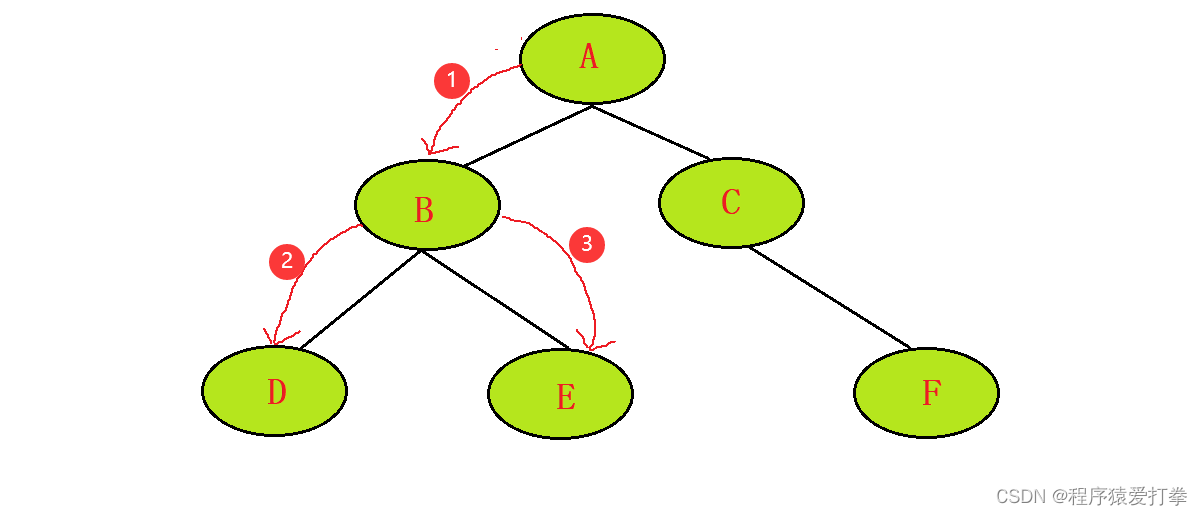
第四步,来到E节点,获取E节点。判断E是否有左子树。有则往下一个节点遍历。没有则遍历右子树,右子树也没有则返回父节点。
此时,发现E节点没有左右子树,则返回到B节点,B节点再返回到A节点,A节点再遍历到C节点,此时遍历到的节点为:ABDE、元素为:1245。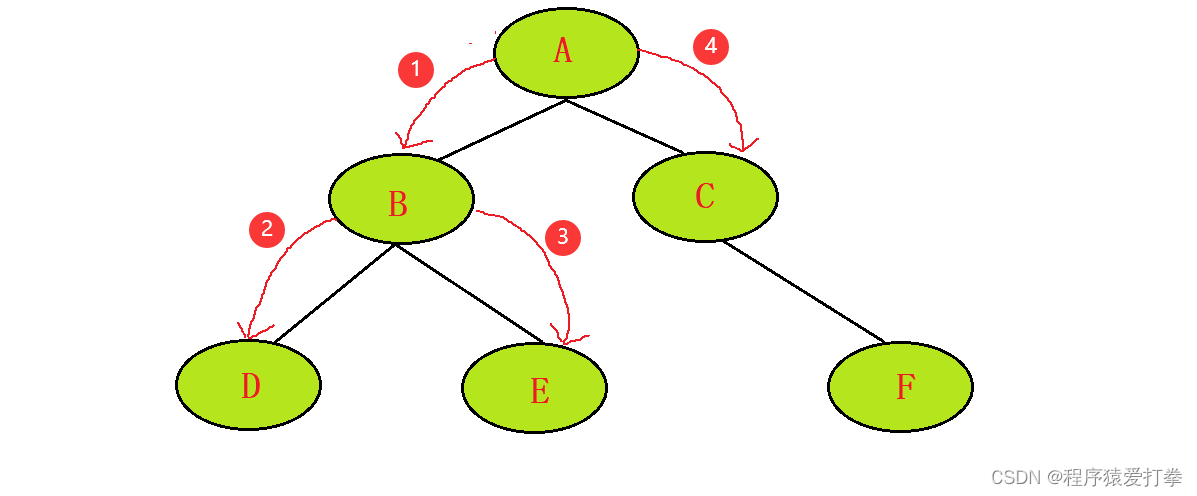
第五步,来到C节点,获取C节点。判断C是否有左子树。有则往下一个节点遍历。没有则遍历右子树,右子树也没有则返回父节点。
此时发现,C节点没有左子树,则访问C节点右子树F节点获取F节点的根节点。往F的左子树进行遍历,此时获取到的节点为:ABDEC,元素为:12453。
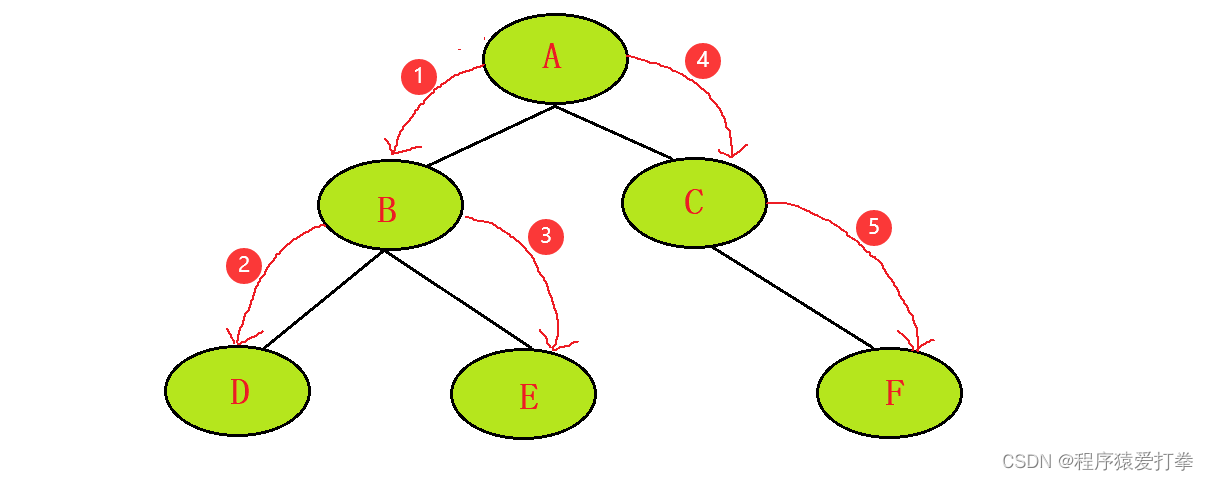
最后一步,来到F节点,获取F节点。F节点没有左右子树,返回F节点的父节点C节点,C节点再返回到C的父节点A节点。最后发现A没有父节点,程序结束。此时获取到的节点为:ABDECF,元素为:124536。
以上就是对前序遍历步骤的一个详细讲解,下面我们来看代码的实现:
//MyBinaryTree.java文件下
public class MyBinaryTree {//静态内部类BinaryTreestatic class BinaryTree {public int val;public BinaryTree left;public BinaryTree right;public BinaryTree(int val) {this.val = val;}}//根节点public BinaryTree root;//创建一个二叉树public void initBinaryTree() {BinaryTree A = new BinaryTree(1);BinaryTree B = new BinaryTree(2);BinaryTree C = new BinaryTree(3);BinaryTree D = new BinaryTree(4);BinaryTree E = new BinaryTree(5);BinaryTree F = new BinaryTree(6);A.left = B;A.right = C;B.left = D;B.right = E;C.right = F;root = A;}//前序遍历二叉树public void preOrder(BinaryTree tree) {if( tree == null) {return;}//节点的元素System.out.print(tree.val+" ");//节点的左子树preOrder(tree.left);//节点的右子树preOrder(tree.right);}
}//Test.java文件下
public class Test {public static void main(String[] args) {MyBinaryTree myBinaryTree = new MyBinaryTree();myBinaryTree.initBinaryTree();myBinaryTree.preOrder(myBinaryTree.root);}
}
运行后输出:

我们可以运行后的结果与上述演练的最终结果是一致的。通过程序我们也不难看出二叉树的遍历是一种递归思想,它的终止条件就是节点本身不为空。另外细心的朋友可以发现前序遍历得到的首结果就是这个二叉树的头节点,因为头节点是第一个被遍历的。
3、中序遍历
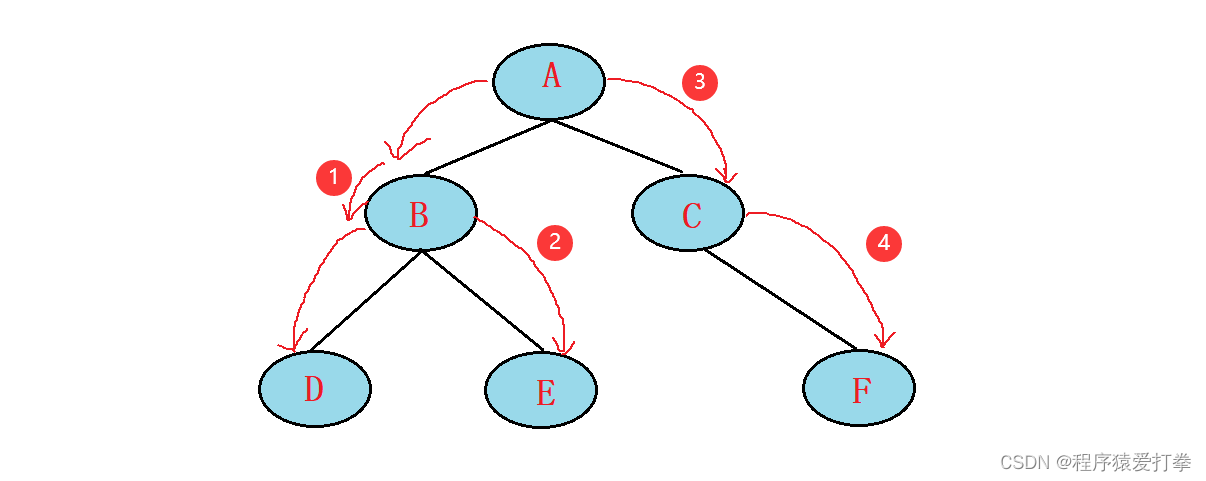
中序遍历的顺序为:根节点的左节点=》根节点=》根节点的右节点。因此,中序遍历本期二叉树得到的根节点顺序为:DBEACF、根节点元素为:425136。
第一步,遍历A的左节点。如果A节点有左节点往A的左节点遍历,不存在则获取A节点,并往A节点的右节点遍历,如果右节点也为空则返回父节点。此时,遍历到了B节点。以下的每个节点也是同此步骤进行的。
第二步,遍历来到B节点。判断B节点的左节点不为空。遍历来到D节点,判断D节点的左子树为空,获取D节点,访问D的右子树为空返回父节点B,获取B节点的根节点。此时遍历到的节点为:DB,元素为:42。
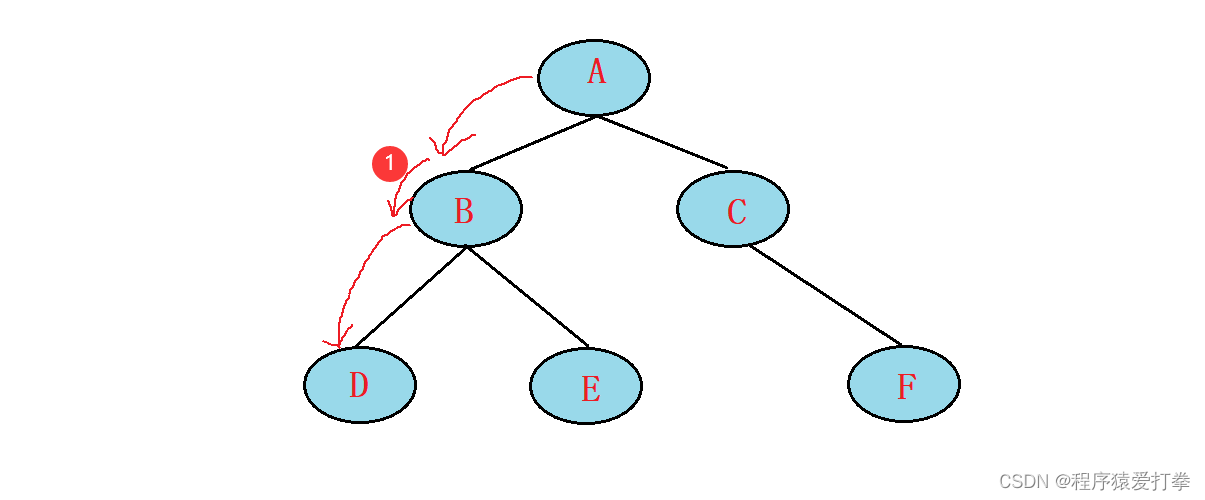
第三步,遍历来到E节点。E节点的左子树为空,获取E节点,右子树也是空返回父节点B,B节点返回父节点A,获取A节点的根节点。此时遍历到的节点为:DBEA,元素为:4251。
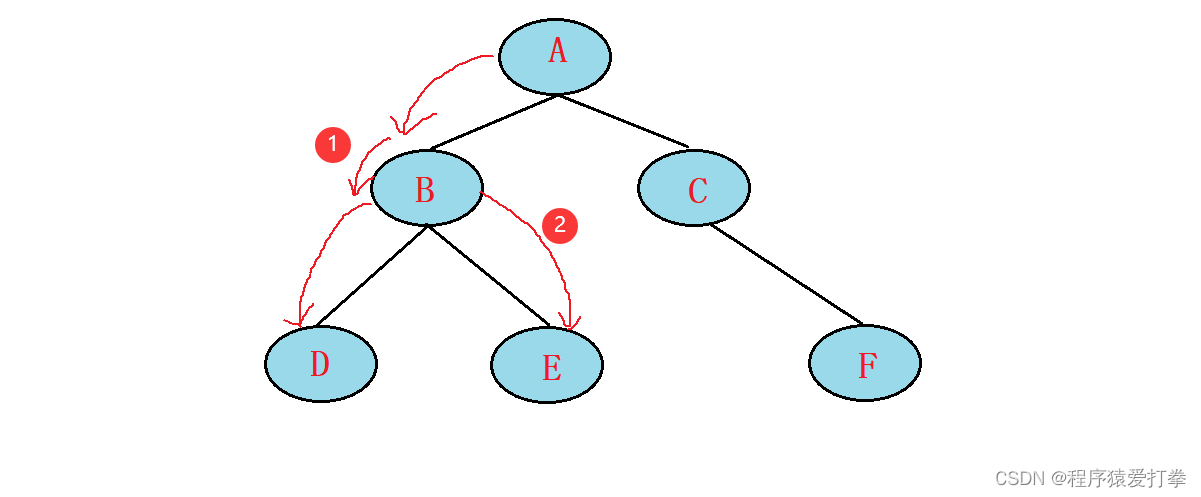
第四步,遍历来到C节点。C节点的左子树为空,获取C节点,判断C节点的右子树不为空。遍历到F节点,此时遍历到的节点为:DBEAC,元素为:42513。
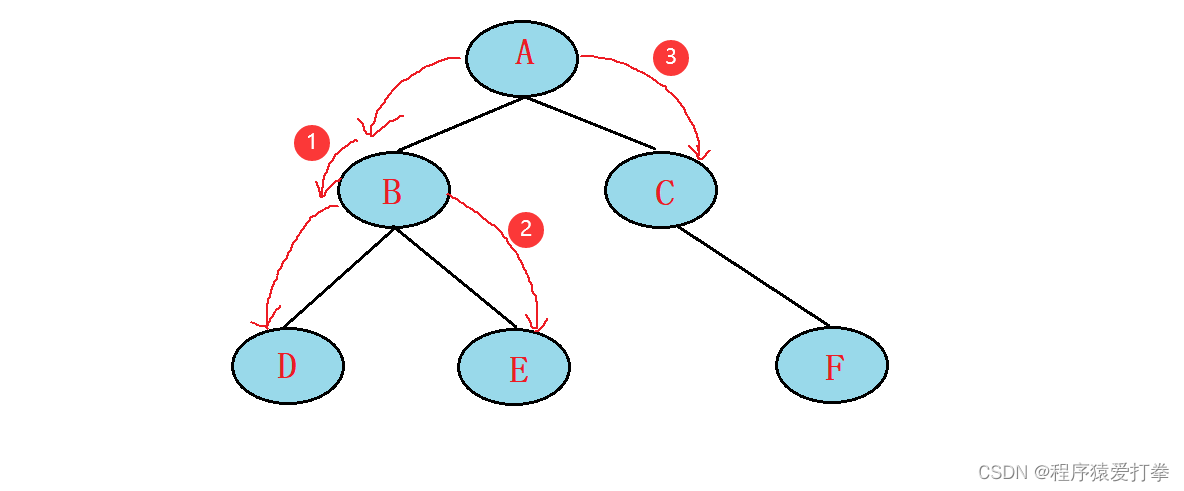
第五步,遍历来到F节点。F节点的左子树为空,获取F节点,F节点的右子树也为空返回父节点C,C节点返回父节点A,A节点没有父节点,程序结束。此时遍历到的节点为:DBEACF,元素为:425136。程序结束。
中序遍历,我们只需将上述代码中的preOrder方法中的访问节点的根节点位置稍微改动一下,其余代码不变。
//中序遍历二叉树
public void inOrder(BinaryTree tree) {if( tree == null) {return;}//节点的左子树preOrder(tree.left);//节点的元素System.out.print(tree.val+" ");//节点的右子树preOrder(tree.right);}运行后输出:

通过上述结果,我们可以看到输出的结果与上方展示的结果是一致。细心的朋友可以发现,当我们中序遍历后头节点的左侧都是左子树,头节点的右侧都是右子树。在上方代码中1的左侧为425,1的右侧为36,正好与我们的二叉树一致。因此,当我们知道了一个二叉树的头节点是谁后可以通过中序遍历推出这个二叉树的左、右则的树。
4、后序遍历
后序遍历的步骤为:根节点的左节点=》根节点的右节点=》根节点,在本篇示例二叉树中对应的遍历节点顺序为:DEBFCA,节点元素为452631。
在上文中,前序遍历与后序遍历我给大家展示了流程图以及实现步骤,其实后序遍历也是一样的按照左节点、右节点、根节点的遍历顺序去遍历,在此博主就不多讲解了,大家可以自己尝试去画图。
后序遍历二叉树的代码,我们也是将preOrder方法中的根节点位置互换一下即可:
//后序遍历二叉树
public void postOrder(BinaryTree tree) {if( tree == null) {return;}//节点的左子树preOrder(tree.left);//节点的右子树preOrder(tree.right);//节点的元素System.out.print(tree.val+" ");}运行后输出:
 通过运行结果可以看到与上方遍历得到的结果是一致的。通过观察,我们也可以知道。知道了一个二叉树的后序遍历,就能得到头节点,因为后序遍历的最后一个数据就是我们的头节点。
通过运行结果可以看到与上方遍历得到的结果是一致的。通过观察,我们也可以知道。知道了一个二叉树的后序遍历,就能得到头节点,因为后序遍历的最后一个数据就是我们的头节点。
当我们知道一个二叉树的前序遍历或后续遍历结果与中序遍历结果时,就能轻易的推出这个二叉树的全貌。
如一个二叉树的前序遍历结果为:ABDECF,中序遍历结果为:DBEACF。则这个二叉树的头节点为:A,左侧子树为:DBE、右侧子树为CF。因此可以推出这个二叉树的全貌为:
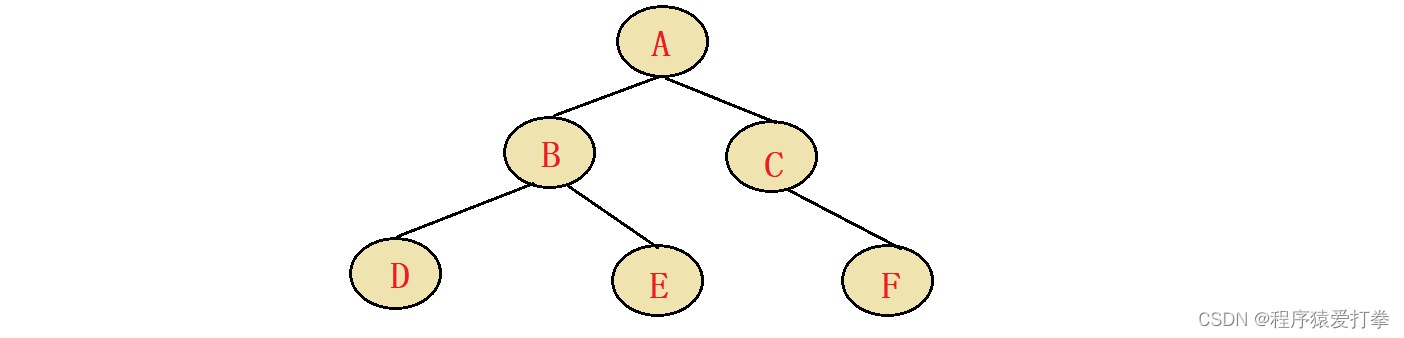
当然,知道一个二叉树的中序遍历与后序遍历也能很轻松的推出这个二叉树,但知道前序遍历和后序遍历却不能推出这个二叉树,因为通过这两个遍历方式我们不能得到左侧、右侧的子树是什么。
本期博客到这里就结束了,大家下来了可以自己去画图理解不懂之处或者私信博主、评论留言都可以。感谢你的阅读,我们下期再见!

相关文章:

数据结构|二叉树的三种遍历方式,你掌握了几种?
目录 1、遍历方式 2、前序遍历 3、中序遍历 1、遍历方式 学习二叉树的结构,最简单的方式就是遍历二叉树。遍历二叉树就是通过某条线路对二叉树的各个结点进行一次访问,访问的方法有三种分为前序遍历、中序遍历、后续遍历,层序遍历它们的遍…...

Direct3D 12——灯光——法向量
a:平面法线着色 b:顶点法线着色 c:像素着色 平面法线(face normal,由于在计算机几何学中法线是有方向的向量,所以也有将normal译作法向量) 是 一种描述多边形朝向(即正交于多边形上所有点)的单位向量。 曲面法线&a…...
)
软考-信息系统工程(五)
信息系统工程 Garlan和Shaw对通用软件架构风格进行了分类,他们将软件架构分为:(曾经考过1分选择题 区分) 数据流风格:数据流风格包括批处理序列和管道/过滤器两种风格。调用/返回风格:调用/返回风格包括主程序/子程序、数据抽象和面向对象,以及层次结构…...
解决谷歌翻译不能使用的问题
今天登录国外网站,发现谷歌翻译已无法正常使用,网上最多的方法就是更改host文件,在host内增加ip地址,但是经常失效,经常手动更改增加ip着实烦恼,还有可能有别的错误。 最终解决方式是:登录GitH…...
Insomnia 简单使用方法
文章目录 1. 新建工程2. 新建若干文件夹3. 设置环境变量4. 授权以及进行请求的链式调用 (chaining requests)4. 1 解决办法 14. 2 解决办法 2 Insomnia 同 Postman, 用于测试后端 endpoint,很容易使用。 使用步骤如下: 1. 新建工程 2. 新建若…...

2023接口自动化测试,完整入门篇
1. 什么是接口测试 顾名思义,接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程,以及相互逻辑依赖关系。其中接口协议分为HTTP,WebService,Dubbo,Thrift,Socket等类型,测试类型又主…...
2023年股票代持行业研究报告
第一章 股票代持概述 1.1 基本概念 股票代持,或称委托持股,是指实际出资人与名义出资人达成以下约定:名义出资人作为名义股东,在股东名册等公司工商登记信息上出现,而实际上由实际出资人出资并享有投资权益。 股票代…...
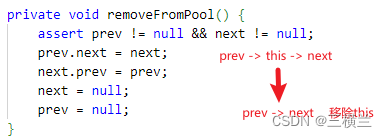
《Netty》从零开始学netty源码(三十九)之PoolSubPage的内存分配
目录 PoolSubPage.allocategetNextAvail方法toHandle方法removeFromPool方法 PoolSubPage.allocate 上一篇我们介绍了PoolSubPage的简单知识,当我们需要PoolSubPage的内存时可调用allocate方法查找可分配二进制的位置,具体的源码过程如下: …...

【目标检测论文阅读笔记】Reducing Label Noise in Anchor-Free Object Detection
(Augmentation for small object detection) Abstract 当前的 anchor-free无锚目标检测器 将空间上落在真值框预定义中心区域内的所有特征标记为正。这种方法会在训练过程中产生 标签噪声,因为这些 正标记的特征中的一些 可能位于背景或遮挡…...

金融数字新型基础设施创新开放联合体今日成立
4月18日,“金融数字新型基础设施创新开放联合体”(以下简称:联合体)在上海成立。联合体由上海银行、复旦大学金融科技研究院、中电金信共同发起,首批成员单位汇聚产业链与供给侧的中坚力量:国泰君安证券、太…...

编程语言的发展史
编程语言处在不断的发展和变化中,从最初的机器语言发展到如今的2500种以上的高级语言,每种语言都有其特定的用途和不同的发展轨迹。编程语言并不像人类自然语言发展变化一样的缓慢而又持久,其发展是相当快速的,这主要是计算机硬件…...

巧用千寻位置GNSS软件|点测量采集技巧
点测量是测量中重要的节点,在测量工作的信息处理分析中发挥着重要作用。本期将给各位带来使用千寻位置GNSS软件采集地形点、控制点、快速点、连续点、房角点和倾斜点的操作技巧。 地形点 地形点的设置如图 5.1-9所 示,每次采集一个点,该点需要…...
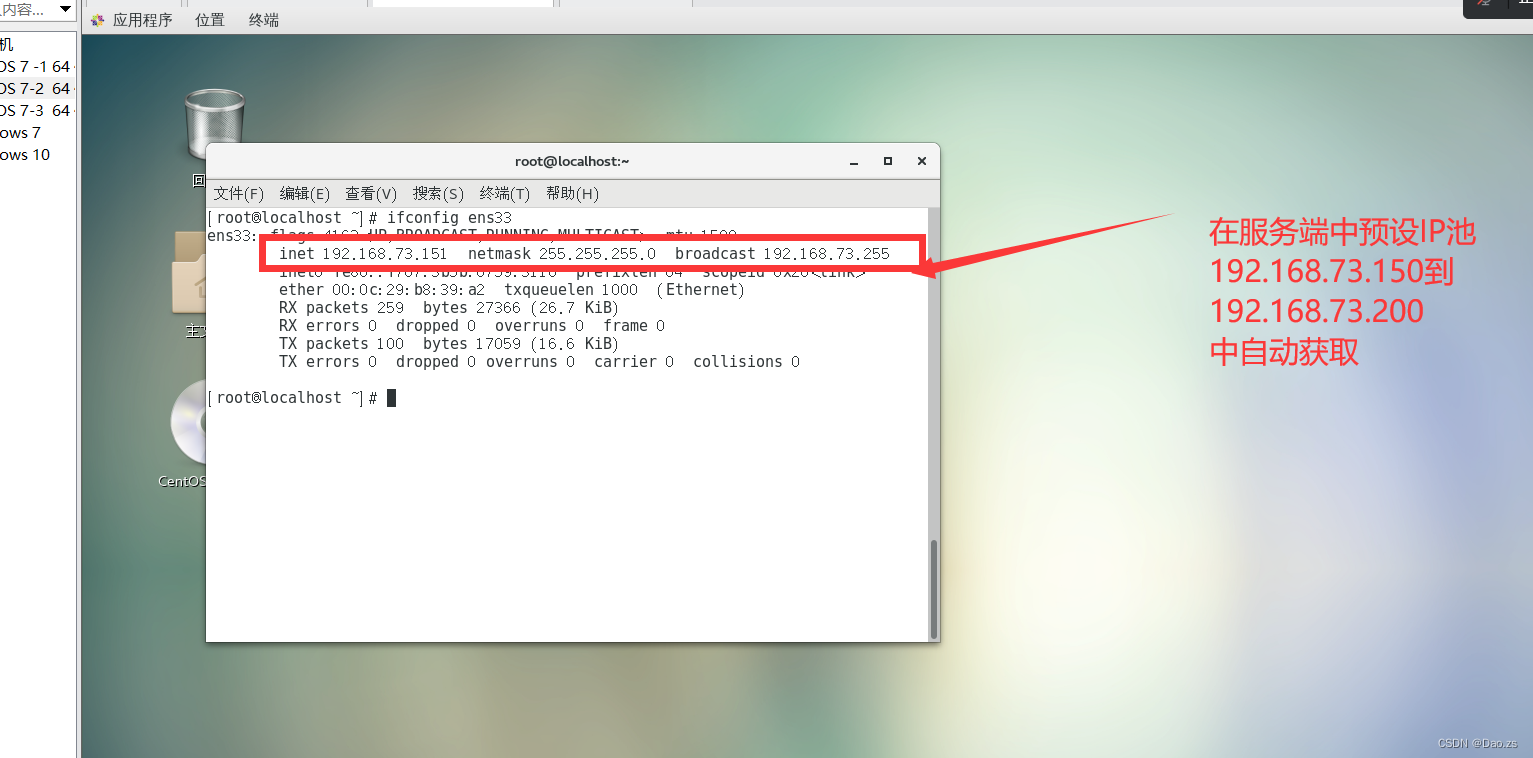
DHCP原理与配置
目录 一、DHCP工作原理 1)了解DHCP服务 使用DHCP的好处 DHCP的分配方式 2)DHCP的租约过程 分为四个步骤 二、DHCP服务器的配置 1)检查并且安装dhcp有关软件包 2)查看系统的配置文件,并且利用好官方给的参考案…...

软件测试今天你被内卷了吗?
认识一个人,大专学历非计算机专业的,是前几年环境好的时候入的行,那时候软件测试的要求真的很低,他那时好像是报了个班,然后入门的,但学的都是些基础,当时的他想的也简单,反正也能拿…...

做完自动化测试,但别让不会汇报毁了你...
pytest 是一个成熟的全功能Python测试工具,可以帮助您编写更好的程序。它与 python 自带的 unittest 测试框架类似,但 pytest 使用起来更简洁和高效,并且兼容 unittest 框架。pytest 能够支持简单的单元测试和复杂的功能测试,pyte…...
企业级信息系统开发讲课笔记2.4 利用MyBatis实现条件查询
文章目录 零、本节学习目标一、查询需求二、打开MyBatisDemo项目三、对学生表实现条件查询(一)创建学生映射器配置文件(二)配置学生映射器文件(三)创建学生映射器接口(四)测试学生映…...
)
【天梯赛—不想坑队友系列】L2-003 月饼(java)
目录 第一题: L2-003 月饼 输入格式: 输出格式: 输入样例: 输出样例: 题目分析 题目代码 第二题:德才论 输入格式: 输出格式: 输入样例: 输出样例ÿ…...
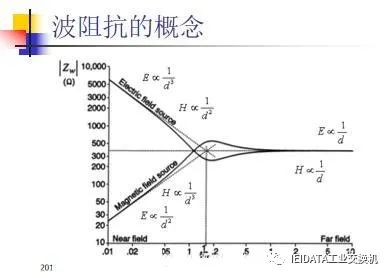
电磁兼容(EMC)的标准与测试内容
在国际范围上,电磁兼容标准的制定已经有了70多年的发展历程,最早为了保护无线电通信和广播,国际无线电干扰特别委员会(CISPR)对各种用电设备和系统提出了相关的电磁干扰发射限值和测量方法。到了20世纪60~7…...

滑动平均算法
class Solution { public static int[] maxSlidingWindow(int[] nums, int k) { int right 0; int[] res new int[nums.length -k 1]; int index0; LinkedList<Integer> list new LinkedList<>(); // 开始构造窗口 …...

个人职业发展
职业的本质就是人和社会的交换关系。选择什么职业,等于选择了用什么方式和世界交换。 比如,快递员、小时工靠“体力”;大多数打工者靠“体力智力”;网红靠“资源、平台”;各领域的大神、科学家、艺术家靠“天赋”。 这…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
