数据结构和算法学习记录——层序遍历(层次遍历)、二叉树遍历的应用(输出二叉树中的叶节点、求二叉树的高度、二元运算表达式树及其遍历、由两种遍历序列确定二叉树)
目录
层序遍历
思路图解
代码实现
二叉树遍历的应用
输出二叉树中的叶节点
代码实现
求二叉树的高度
思路图解
代码实现
二元运算表达式树及其遍历
由两种遍历序列确定二叉树
层序遍历
层序遍历可以通过一个队列来实现,其基本过程为:
先根节点入队,然后:
- 从队列中取出一个元素;
- 访问该元素所指的节点;
- 若该元素所指节点的左、右孩子节点非空, 则将其左、右孩子的指针顺序入队。
- 循环123的步骤,直到队列为空。
思路图解
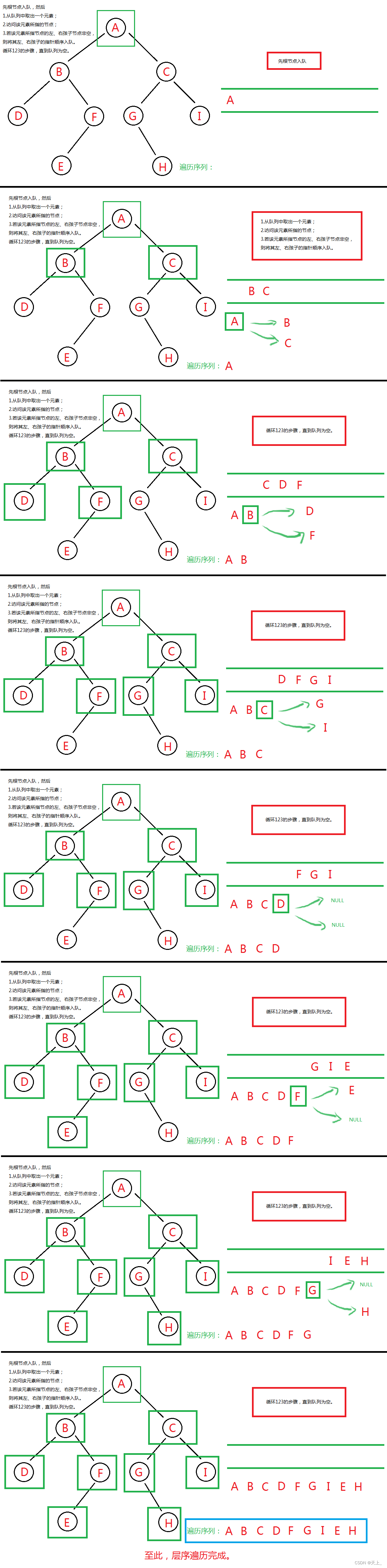
代码实现
void LevelOrderTraversal(BinTree BT)
{Queue Q;BinTree T;if (!BT){return; //若为空树则直接返回}Q = CreateQueue(); //创建并初始化队列QAdd(Q, BT);while (!IsEmptyQ(Q)){T = DeleteQ(Q);printf("%d\n", T->data); //访问取出来的节点//若该元素的左右孩子节点不为空,则依次入队if (T->Left){AddQ(Q, T->Left); }if (T->Right){AddQ(Q, T->Right);}}
}
二叉树遍历的应用
输出二叉树中的叶节点
之前讲过的递归先序遍历二叉树写法很简单,而要输出二叉树中的叶节点,就可以在进行遍历的过程中进行检测,如果为叶节点则输出,否则继续遍历。 叶节点即左孩子节点为空、右孩子节点也为空。
代码实现
void PreOrderPrintLeaves(BinTree BT)
{if (BT){if (!BT->Left && !BT->Right)printf("%d ", BT->data);PreOrderPrintLeaves(BT->Left);PreOrderPrintLeaves(BT->Right);}
}求二叉树的高度
树是递归定义的,一颗二叉树的高度应该等于左右两颗子树的最大高度+1 求二叉树的高度,利用的是后序遍历的一种程序框架来实现的。

思路图解
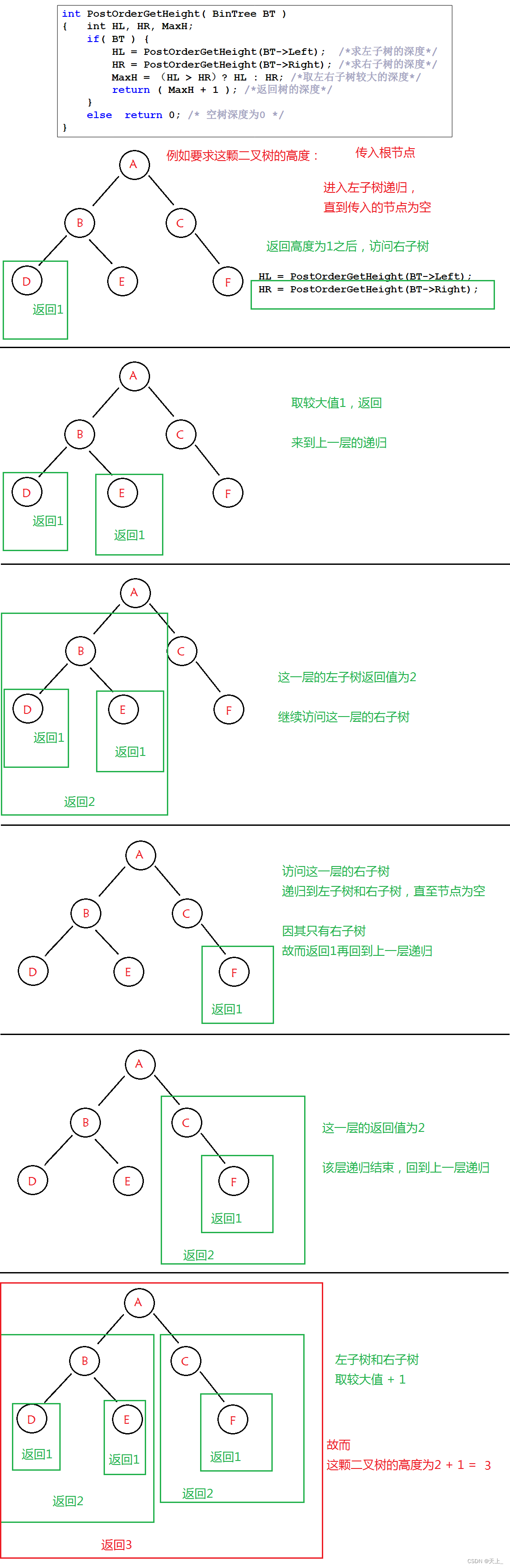
代码实现
int PostOrderGetHeight(BinTree BT)
{int HL, HR, MaxH;if (BT){HL = PostOrderGetHeight(BT->Left); //求左子树的高度HR = PostOrderGetHeight(BT->Right); //求右子树的高度MaxH = (HL > HR) ? HL : HR; //取左右子树的最大高度return (MaxH + 1); //返回树的高度}else{return 0; //空树的高度为0}
}
二元运算表达式树及其遍历
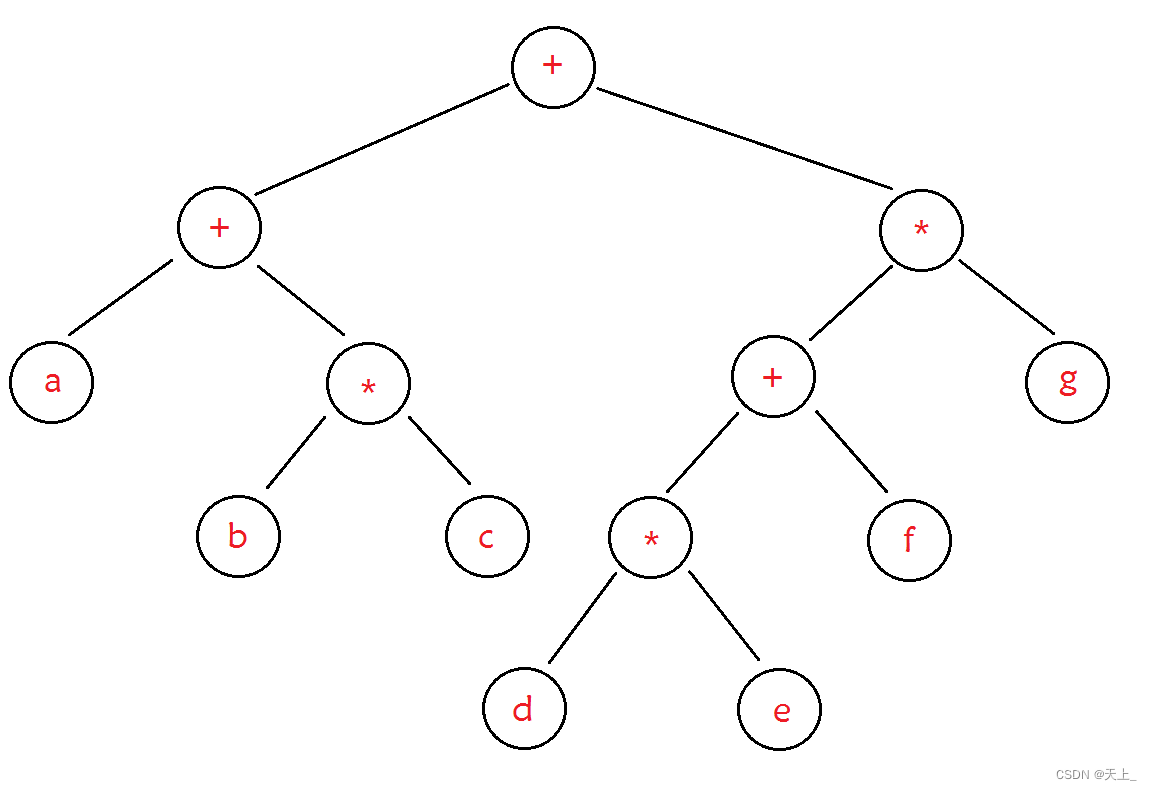
对上面的表达式树进行三种遍历,可以得到三种不同的访问结果:
试着分别写出上面表达式树前序中序和后序遍历的不同表达式,复习一遍之前讲的树的遍历。
先序遍历可以得到前缀表达式:++a*bc*+*defg
中序遍历可以得到中缀表达式:a+b*c+d*e+f*g
后序遍历可以得到后缀表达式:abc*+de*f+g*+
但需要注意的是:中缀表达式会受到运算符优先级的影响,所以单单这样通过中序遍历得出的中缀表达式是不完全准确的。
解决方法是:在输出左子树之前,先输出一个左括号,左子树结束的时候再输出一个右括号。
由两种遍历序列确定二叉树
已知三种遍历中的任意两种遍历序列,能否唯一确定一颗二叉树呢?
答案是:两种遍历序列中,必须要有一种是中序遍历才能够唯一确定一颗二叉树。
假设没有中序,看下面两个序列:
先序遍历序列:A B
后序遍历序列:B A
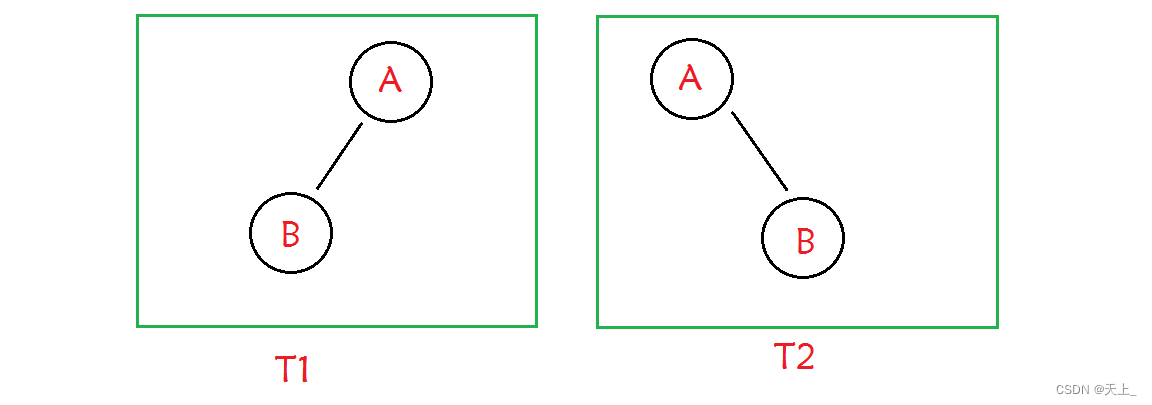
像这样一组简单的序列,只有先序遍历序列和后序遍历序列的情况下,就有两颗是符合的二叉树,其中根节点是容易确定的,先序的第一个节点就是根,后序的最后一个节点就是根;但是左右节点是不好区分的,所以就导致了只有先序序列和后序序列的情况下没法唯一地确认一颗二叉树。
下面就来看看,已知先序序列和中序序列,怎么样来确定一颗二叉树。
思路:
- 根据先序遍历序列第一个节点确定根节点;
- 根据根节点在中序遍历序列中分割出左右两个子序列;
- 对左子树和右子树分别递归使用相同的方法继续分解。

举个例子清晰一下思路:
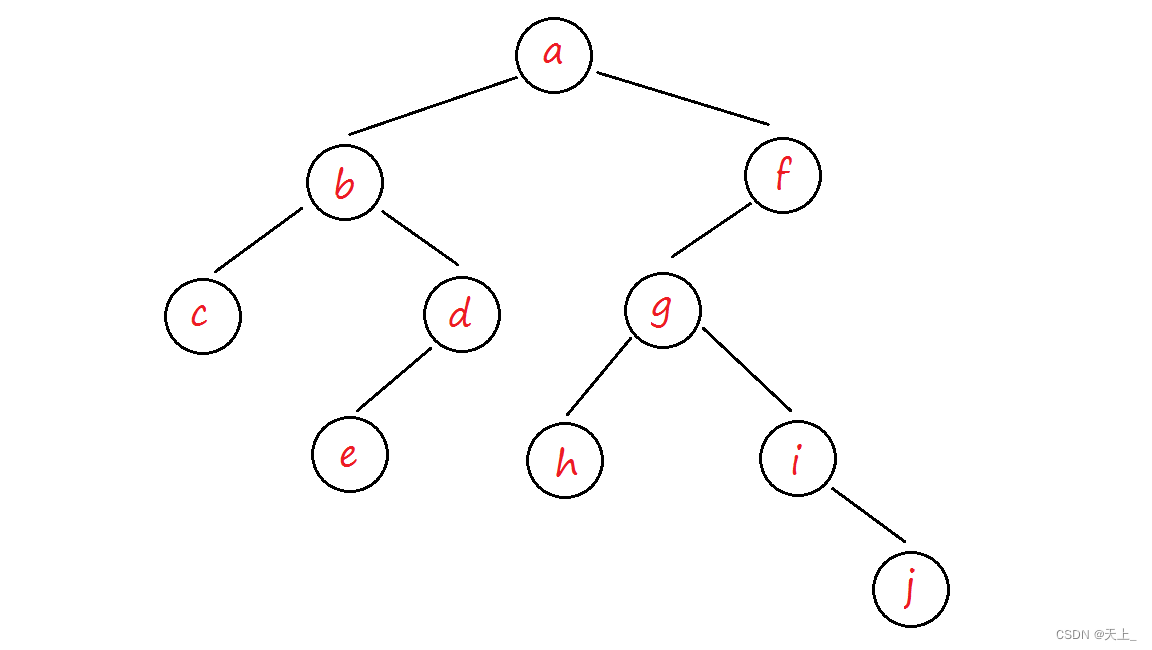
先序序列: abcdefghij
中序序列: cbedahgijf

所以最终通过先序遍历序列和中序遍历序列唯一确定的二叉树就为:
end
学习自:MOOC数据结构——陈越、何钦铭
相关文章:

数据结构和算法学习记录——层序遍历(层次遍历)、二叉树遍历的应用(输出二叉树中的叶节点、求二叉树的高度、二元运算表达式树及其遍历、由两种遍历序列确定二叉树)
目录 层序遍历 思路图解 代码实现 二叉树遍历的应用 输出二叉树中的叶节点 代码实现 求二叉树的高度 思路图解 代码实现 二元运算表达式树及其遍历 由两种遍历序列确定二叉树 层序遍历 层序遍历可以通过一个队列来实现,其基本过程为: 先根…...
、查询、删除数据库等操作解析(Cypher语句))
【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除数据库等操作解析(Cypher语句)
【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除操作解析(Cypher语句) 文章目录 【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除操作解析(Cypher语句)1. 介绍2…...
命令)
Linux移动文件和文件夹(目录)命令
命令mv 英文move 翻译移动 mv命令可以移动文件或文件夹(目录),也可以重命令(覆盖)文件。 1. 移动文件/重命名 单纯地移动某一个文件直接使用: mv <源文件名称/地址> <新文件名称/地址>这个方法…...

Pandas的应用-5
Pandas是一个强大的数据处理库,它提供了高性能、易于使用的数据结构和数据分析工具。本文将介绍Pandas常用的数据结构和常用的数据分析技术,包括DataFrame的应用、窗口计算、相关性判定、Index的应用、范围索引、分类索引、多级索引以及日期时间索引。 …...

java继承类怎么写
继承类是通过把父类的方法和属性继承到一个类中,而子类的方法和属性是子类自己定义的。 Java中有一个很重要的概念叫做继承,这也是 Java语言的精髓所在。Java语言提供了一种机制,叫做派生类。在 Java中,如果没有实现了某个派生类方…...

面向对象程序设计
OOP 【面向对象程序设计】(OOP)与【面向过程程序设计】在思维方式上存在着很大的差别。【面向过程程序设计】中,算法是第一位的,数据结构是第二位的,这就明确地表述了程序员的工作方式。首先要确定如何操作数据&#…...
)
Linux 用户身份切换(su,sudo)
文章目录 Linux 用户身份切换su使用案例 sudo使用案例 visudo与/etc/sudoers单一用户可使用root所有命令,与sudoers文件语法利用wheel用户组以免密码的功能处理visudo有限制的命令操作通过别名创建visudosudo的时间间隔问题sudo搭配su的使用方式 Linux 用户身份切换…...

求倒置数问题
文章目录 求倒置数程序设计程序分析求倒置数 【问题描述】数组A【0,…,n-1】是一个n个不同整数数构成的数组。如果i<j,但是A[i]〉A[j],则这对元素(A[i],A[j])被称为一个倒置(inversion)。设计一个O(nlogn)算法来计算数组中的倒置数量 【输入形式】输入两行,第一行…...
)
sed(学习)
1、清除环境变量 profile~/.bash_profile sed -i s#export LD_LIBRARY_PATH.*##g $profile 2、设置环境变量(替换值) sed -i s#export LD_LIBRARY_PATH.*#export LD_LIBRARY_PATH/opt/testlinux/lib#g ~/.bash_profile 3、修改配置文件 sdk_dir/root/test log_dir/…...

B - GCD Subtraction
文章目录 AtCoder Regular Contest 159B - GCD Subtraction AtCoder Regular Contest 159 B - GCD Subtraction 问题:每次A,B都减去gcd(A,B),求其中一个减到0至少需要多少次主要思路: 首先第一步应该想到每次减去的数,先减去的数…...

解决Failed to load ApplicationContext问题的思路
中文翻译: 加载ApplicationContext失败 第一步:首先检查测试类的注解 以及 依赖 SpringBootTest <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-test</artifactId><scop…...

基于CAMX大气臭氧来源解析模拟与臭氧成因分析实践技术应用
查看原文>>>基于CAMX大气臭氧来源解析模拟与臭氧成因分析实践技术应用 目录 专题一、大气臭氧污染来源及成因分析技术讲解;CAMx模式初识及臭氧来源解析模拟本地案例配置说明 专题二、CAMx模式编译安装及空气质量模拟案例配置 专题三、CAMx扩展和探测工…...
)
异常的讲解 (1)
目录 异常入门的案例 异常介绍 基本概念 异常的小结 常见的运行时异常 1.NullPointerException空指针异常 2.ArithmeticException数学运算异常 3.ArraylndexOutOfBoundsException数组下标越界异常 4.ClassCastException类型转换异常 5.NumberFormatException数字格式不…...
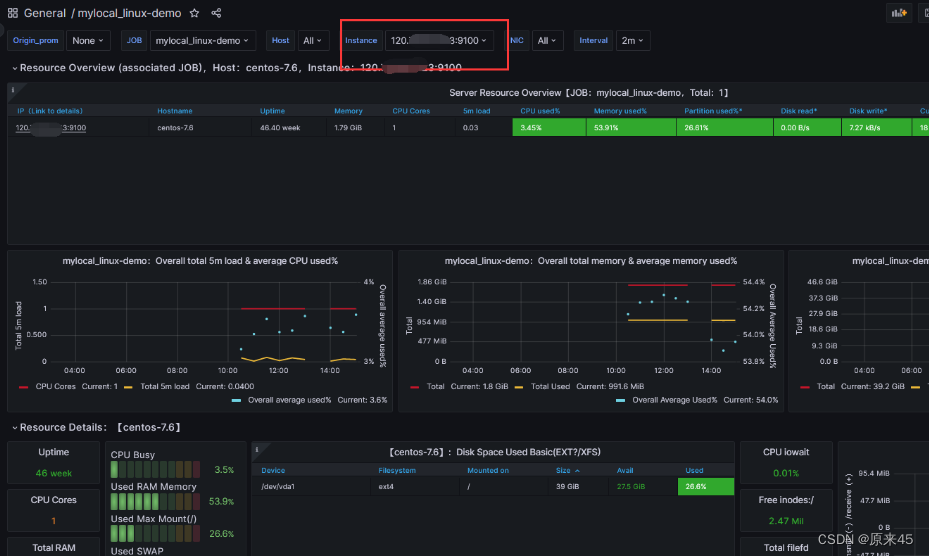
Prometheus - Grafana 监控 MySQLD Linux服务器 demo版
目录 首先是下载Prometheus 下载和安装 配置Prometheus 查看监控数据 监控mysql demo 部署 mysqld_exporter 组件 配置 Prometheus 获取监控数据 -------------------------------------- 安装和使用Grafana 启动Grafana -------------------------------------- 配…...
应届生,实力已超6年,太卷了!
你好,我是田哥 今晚上,给一位朋友做模拟面试,原本说好的90分钟左右,结果整了2个多小时。 很多人估计也很好奇,我们这两个多小时聊聊什么,下面我给大致总结一下: 面试技巧 面试中,我们…...

0-1背包问题
文章目录 0-1背包问题JavaPython0-1背包问题 【问题描述】 给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大? 【输入形式】 第一行输入物品的个数n和背包容量C。 第二行输入每个物品的价值v[i…...
VUE前端项目环境搭建
背景: 想要使用vue搭建一个前端项目,写个小网站练练手,因为没有前端经验,所以从网上找了一个vue得开源模板使用,经过一番挑选选中了字节公司花裤衩大佬开源得项目,地址如下: 开源项目地址&…...

VMware安装Win2000安装程序闪退重启等问题的解决方法
VMware安装Win2000安装程序闪退重启等问题的解决方法 【症状】 1、比较新的VMware版本如16.2.5,Win2000安装时,安装程序在安装Distributed Transaction Coordinator时闪退重启 2、比较新的VMware版本如17.0.1,还会发生显示跳跃性卡顿的现象…...
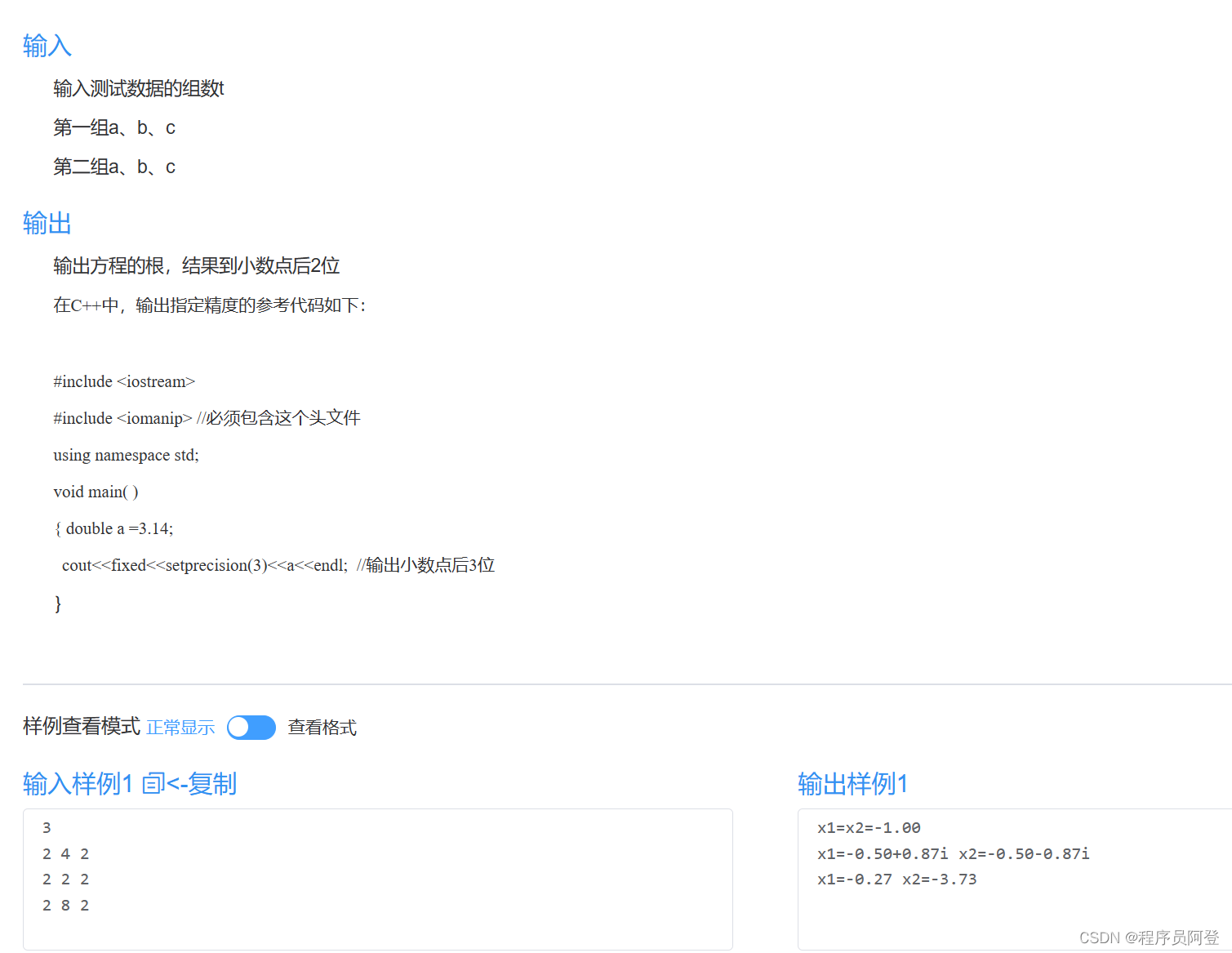
【id:45】【20分】A. Equation(类与对象+构造)
题目描述 建立一个类Equation,表达方程ax2bxc0。类中至少包含以下方法: 1、无参构造(abc默认值为1.0、1.0、0)与有参构造函数,用于初始化a、b、c的值; 2、set方法,用于修改a、b、c的值 3、ge…...

数据库事务
什么是事务 在数据库中,事务(Transaction)是指一组数据库操作,这些操作要么全部成功执行,要么全部失败回滚,是保证数据库操作一致性的基本单位。事务具有原子性(Atomicity)、一致性…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
