浅谈根号分治与分块
文章目录
- 1. 根号分治
- 哈希冲突
- 2. 线性分块
- 引入
- 教主的魔法
- [CQOI2011] 动态逆序对
- [国家集训队] 排队
- [HNOI2010] 弹飞绵羊
- 蒲公英
1. 根号分治
哈希冲突
题目1
n n n 个数, m m m 次操作。操作 1 为修改某一个数的值,操作 2 为查询所有满足下标模 x x x 等于 y y y 的数之和。
先来看两个暴力算法:
-
算法 1:
修改:直接修改。时间复杂度 O ( 1 ) O(1) O(1) 。
查询:枚举下标模 x x x 等于 y y y 的数的和。时间复杂度 O ( n ) O(n) O(n) 。 -
算法 2:
先预处理出 f ( i , j ) f(i,j) f(i,j) 表示下标模 i i i 等于 j j j 的数之和。时间复杂度 O ( n 2 ) O(n^2) O(n2) 。
修改:修改所有 i i i 下的 f ( i , x m o d i ) f(i,x\bmod i) f(i,xmodi)。时间复杂度 O ( n ) O(n) O(n)
查询:直接查询。时间复杂度 O ( 1 ) O(1) O(1)。
容易想到划定一个界限 B B B 选择使用的算法。
当 x x x 较大时,即 x > B x>B x>B 时,算法 1 的查询次数会较小,复杂度 O ( N B ) O(\frac N B) O(BN) 。
当我们仅用算法 2 处理模数 i i i 较小的情况时,即 i ≤ B i\le B i≤B 时,算法 2 复杂度会较低,预处理复杂度 O ( B 2 ) O(B^2) O(B2),修改复杂度 O ( B ) O(B) O(B)。
总时间复杂度 O ( B 2 + m ( N B + B ) ) O(B^2+m(\frac N B + B)) O(B2+m(BN+B))。在 B = N B=\sqrt N B=N 时复杂度最低。
代码
2. 线性分块
引入
题目
给定 n n n 个数 a [ 1.. n ] a[1..n] a[1..n], m m m 次操作,区间修改,区间查询。
我们将数列分段,设块长为 B B B。
对于区间 [ L , R ] [L,R] [L,R] 的询问:
-
若 L , R L,R L,R 在同一个块内,直接暴力枚举 [ L , R ] [L,R] [L,R] 统计。
-
若 L , R L,R L,R 不在同一个块内,则将 [ L , R ] [L,R] [L,R] 分成左右两个散块以及中间若干整块。对于每个整块,我们事先预处理出每个整块的 b i = ∑ a i b_i=\sum a_i bi=∑ai。对于散块,暴力统计。
时间复杂度至多 O ( B + N B ) O(B+\frac N B) O(B+BN) 。
对于区间 [ L , R ] [L,R] [L,R] 的修改:
-
若 L , R L,R L,R 在同一个块内,直接暴力枚举 [ L , R ] [L,R] [L,R] 修改。
-
若 L , R L,R L,R 不在同一个块内,则将 [ L , R ] [L,R] [L,R] 分成左右两个散块以及中间若干整块。对于每个整块,我们修改整块的 b i b_i bi。对于散块,暴力修改。
时间复杂度至多 O ( B + N B ) O(B+\frac N B) O(B+BN) 。
B = N B=\sqrt N B=N 时最优。
代码
教主的魔法
题目
给定 n n n 个数, m m m 次操作。区间修改,区间查询有多少个数 ≥ k \ge k ≥k。
设块长为 B B B。
-
对于区间 [ L , R ] [L,R] [L,R] 的询问:
与上题基本一样,但是我们需要快速统计出整块中有多少个 ≥ k \ge k ≥k 的数。考虑将所有整块内元素排序后二分查找。
时间复杂度至多 O ( B + N B log B ) O(B+\frac N B \log B) O(B+BNlogB) 。
-
对于区间 [ L , R ] [L,R] [L,R] 的修改:
修改整块并不会改变排序后的相对位置,记录标记表示增加的量即可。
而对于散块的修改,可能会改变所在块的相对位置,我们暴力修改后重新排序。
时间复杂度至多 O ( B + log B + N B ) O(B +\log B + \frac N B) O(B+logB+BN) 。
复杂度最低时, B B B 的大小应该为 N \sqrt N N 左右(略大于 N \sqrt N N,取 N \sqrt N N 也能过)。
代码
同类题 :Array Transformer (附代码)
[CQOI2011] 动态逆序对
题目
给定 n n n 个数的一个排列, m m m 此操作。每次删一个数,问删前逆序对个数。
删除一个数后,逆序对数量会减少这个数的贡献。第 i i i 个数的贡献为 [ 1 , i ) [1,i) [1,i) 中比 i i i 大的个数加上 ( i , n ] (i,n] (i,n] 中比 i i i 小的个数。和上一题类似,可以用二分或者树状数组解决。
代码
[国家集训队] 排队
题目
给定 n n n 个数 h 1 . . . h n h_1...h_n h1...hn , m m m 次操作。每次操作交换两个数,问操作前的逆序对个数。
和上一题一样,考虑两个数交换前和交换后的贡献。
代码
双倍经验 :Anton and Permutation (附代码)
[HNOI2010] 弹飞绵羊
题目
题意见题面。
考虑预处理出 s t e p [ x ] step[x] step[x] 表示从 x x x 处开始弹几步能弹到下一块, p o s [ x ] pos[x] pos[x] 表示从 x x x 开始第一次弹到下一块的位置在哪里。
查询:每次跳到下一块,复杂度为 O ( N B ) O(\frac N B) O(BN) 。
修改:记修改点为 x x x ,所在块为 B B B ,块对应区间为 [ L B , R B ] [L_B,R_B] [LB,RB] ,那么可能会对 [ L B , x ] [L_B,x] [LB,x] 上的点的 p o s pos pos 和 s t e p step step 造成影响。复杂度 O ( B ) O(B) O(B)。
B = N B=\sqrt N B=N 。
代码
双倍经验 :Holes (附代码)
蒲公英
题目
静态求区间众数,强制在线。
分析:
-
n ≤ 4 × 1 0 4 , a ≤ 1 0 9 n\le 4 \times 10 ^ 4, a\le 10^9 n≤4×104,a≤109 ,考虑离散化。
-
由于众数不满足一些性质(如可加性等),无法方便的用一些数据结构维护出来,考虑分块。
Solution
我们将序列分成 K K K 段,每段长度 N K \frac {N}{K} KN (左右)。
对于一次询问 [ l , r ] [l,r] [l,r] ,将其划分为若干整块和两块散块:
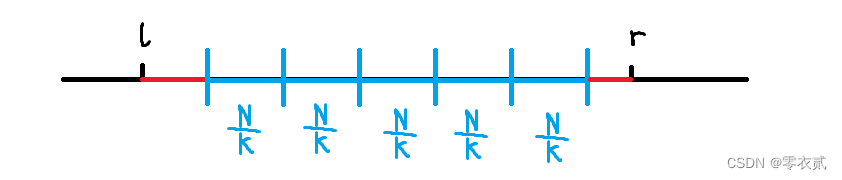
那么,答案一定为蓝色区间的众数或者红色区间出现过的数字。
考虑预处理出任意 i i i 到 j j j 块间的众数,来快速求出蓝色区间的众数,预处理时间复杂度 O ( K 2 N ) O(K^2N) O(K2N)。
// cnt[i][j][x] : x 在 i 到 j 块间出现的次数
// num[i][j] : i 到 j 块间的众数for(int i=1; i<=n; i++){int B = ceil((1.0 * i) / (1.0 * len));belong[i] = B;cnt[B][B][a[i]] ++ ;}for(int i=1; i<=n; i++){int B = ceil((1.0 * i) / (1.0 * len));if(cnt[B][B][a[i]] == cnt[B][B][num[B][B]] && a[i] < num[B][B]) num[B][B] = a[i];if(cnt[B][B][a[i]] > cnt[B][B][num[B][B]]) num[B][B] = a[i];}for(int i=1; i<=k; i++)for(int j=i+1; j<=k; j++)for(int x=1; x<=tot; x++){cnt[i][j][x] = cnt[i][j-1][x] + cnt[j][j][x];if(cnt[i][j][x] == cnt[i][j][num[i][j]] && x < num[i][j]) num[i][j] = x;if(cnt[i][j][x] > cnt[i][j][num[i][j]]) num[i][j] = x;}对于每次询问,我们 O ( 1 ) O(1) O(1) 求蓝色区间的众数, O ( N K ) O(\frac N K) O(KN) 枚举红色区间的数,计算 [ l , r ] [l,r] [l,r] 的众数,询问时间复杂度 O ( M N K ) O(M \frac N K) O(MKN)。
总时间复杂度 O ( N K 2 + M N K ) O(NK^2+M \frac N K) O(NK2+MKN),如果我们认为 N , M N,M N,M 同构,那么 K = N 1 3 K=N^{\frac 1 3} K=N31 时复杂度最低。
代码
相关文章:

浅谈根号分治与分块
文章目录 1. 根号分治哈希冲突 2. 线性分块引入教主的魔法[CQOI2011] 动态逆序对[国家集训队] 排队[HNOI2010] 弹飞绵羊蒲公英 1. 根号分治 哈希冲突 题目1 n n n 个数, m m m 次操作。操作 1 为修改某一个数的值,操作 2 为查询所有满足下标模 x x x …...
(OpenAI)ChatGPT注册登录常见问题错误代码及其解决方法
在使用 ChatGPT 的时候我们可能会碰到一些错误的代码,本文统一来介绍一下每一种错误以及解决方法。 错误代码1. 不能在当前国家使用 出现场景:一般在注册或登录的时候会出现。 原因:主要是ChatGPT检测到当前访问所在的地区不允许访问导致。 …...
MySQL主从复制、读写分离(MayCat2)实现数据同步
文章目录 1.MySQL主从复制原理。2.实现MySQL主从复制(一主两从)。3.基于MySQL一主两从配置,完成MySQL读写分离配置。(MyCat2) 1.MySQL主从复制原理。 MySQL主从复制是一个异步的复制过程,底层是基于Mysql数…...

Linux 云服务器好用吗?(解读Linux云服务器的特点优势)
如今,云计算越来越受欢迎,许多公司正在将业务转移到那里。企业向云过渡的主要原因是它提供的众多服务,包括安全和充足的存储、数据库、服务器和其他关键元素。 作为相对前|沿的技术之一,云建立在虚拟服务器上。Linux 服务器…...
研读Rust圣经解析——Rust learn-8(match,if-let简洁控制流,包管理)
研读Rust圣经解析——Rust learn-8(match,if-let简洁控制流,包管理) matchother和占位符_区别 easy matchenum matchno valuematch inner Option matchmore better way if-let整洁控制包管理模块(mod)拆分声明modpub公开use展开引用拆解模块结…...

G8期刊《全体育》期刊简介及投稿要求
G8期刊《全体育》期刊简介及投稿要求 《全体育》是由湖南体育产业集团有限公司主管、体坛传媒集团股份有限公司主办、中教体育 出版发行的体育综合性期刊。 主管:湖南体育产业集团有限公司 主办:体坛传媒集团股份有限公司 国内刊号:CN4…...
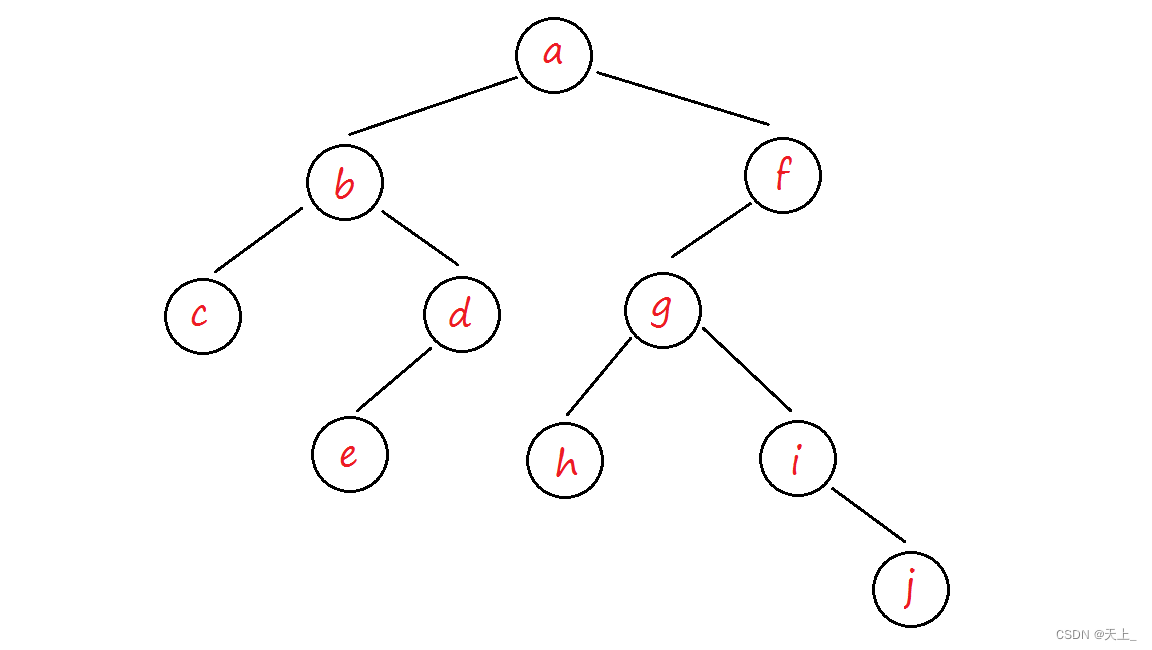
数据结构和算法学习记录——层序遍历(层次遍历)、二叉树遍历的应用(输出二叉树中的叶节点、求二叉树的高度、二元运算表达式树及其遍历、由两种遍历序列确定二叉树)
目录 层序遍历 思路图解 代码实现 二叉树遍历的应用 输出二叉树中的叶节点 代码实现 求二叉树的高度 思路图解 代码实现 二元运算表达式树及其遍历 由两种遍历序列确定二叉树 层序遍历 层序遍历可以通过一个队列来实现,其基本过程为: 先根…...
、查询、删除数据库等操作解析(Cypher语句))
【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除数据库等操作解析(Cypher语句)
【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除操作解析(Cypher语句) 文章目录 【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除操作解析(Cypher语句)1. 介绍2…...
命令)
Linux移动文件和文件夹(目录)命令
命令mv 英文move 翻译移动 mv命令可以移动文件或文件夹(目录),也可以重命令(覆盖)文件。 1. 移动文件/重命名 单纯地移动某一个文件直接使用: mv <源文件名称/地址> <新文件名称/地址>这个方法…...

Pandas的应用-5
Pandas是一个强大的数据处理库,它提供了高性能、易于使用的数据结构和数据分析工具。本文将介绍Pandas常用的数据结构和常用的数据分析技术,包括DataFrame的应用、窗口计算、相关性判定、Index的应用、范围索引、分类索引、多级索引以及日期时间索引。 …...

java继承类怎么写
继承类是通过把父类的方法和属性继承到一个类中,而子类的方法和属性是子类自己定义的。 Java中有一个很重要的概念叫做继承,这也是 Java语言的精髓所在。Java语言提供了一种机制,叫做派生类。在 Java中,如果没有实现了某个派生类方…...

面向对象程序设计
OOP 【面向对象程序设计】(OOP)与【面向过程程序设计】在思维方式上存在着很大的差别。【面向过程程序设计】中,算法是第一位的,数据结构是第二位的,这就明确地表述了程序员的工作方式。首先要确定如何操作数据&#…...
)
Linux 用户身份切换(su,sudo)
文章目录 Linux 用户身份切换su使用案例 sudo使用案例 visudo与/etc/sudoers单一用户可使用root所有命令,与sudoers文件语法利用wheel用户组以免密码的功能处理visudo有限制的命令操作通过别名创建visudosudo的时间间隔问题sudo搭配su的使用方式 Linux 用户身份切换…...

求倒置数问题
文章目录 求倒置数程序设计程序分析求倒置数 【问题描述】数组A【0,…,n-1】是一个n个不同整数数构成的数组。如果i<j,但是A[i]〉A[j],则这对元素(A[i],A[j])被称为一个倒置(inversion)。设计一个O(nlogn)算法来计算数组中的倒置数量 【输入形式】输入两行,第一行…...
)
sed(学习)
1、清除环境变量 profile~/.bash_profile sed -i s#export LD_LIBRARY_PATH.*##g $profile 2、设置环境变量(替换值) sed -i s#export LD_LIBRARY_PATH.*#export LD_LIBRARY_PATH/opt/testlinux/lib#g ~/.bash_profile 3、修改配置文件 sdk_dir/root/test log_dir/…...

B - GCD Subtraction
文章目录 AtCoder Regular Contest 159B - GCD Subtraction AtCoder Regular Contest 159 B - GCD Subtraction 问题:每次A,B都减去gcd(A,B),求其中一个减到0至少需要多少次主要思路: 首先第一步应该想到每次减去的数,先减去的数…...

解决Failed to load ApplicationContext问题的思路
中文翻译: 加载ApplicationContext失败 第一步:首先检查测试类的注解 以及 依赖 SpringBootTest <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-test</artifactId><scop…...

基于CAMX大气臭氧来源解析模拟与臭氧成因分析实践技术应用
查看原文>>>基于CAMX大气臭氧来源解析模拟与臭氧成因分析实践技术应用 目录 专题一、大气臭氧污染来源及成因分析技术讲解;CAMx模式初识及臭氧来源解析模拟本地案例配置说明 专题二、CAMx模式编译安装及空气质量模拟案例配置 专题三、CAMx扩展和探测工…...
)
异常的讲解 (1)
目录 异常入门的案例 异常介绍 基本概念 异常的小结 常见的运行时异常 1.NullPointerException空指针异常 2.ArithmeticException数学运算异常 3.ArraylndexOutOfBoundsException数组下标越界异常 4.ClassCastException类型转换异常 5.NumberFormatException数字格式不…...
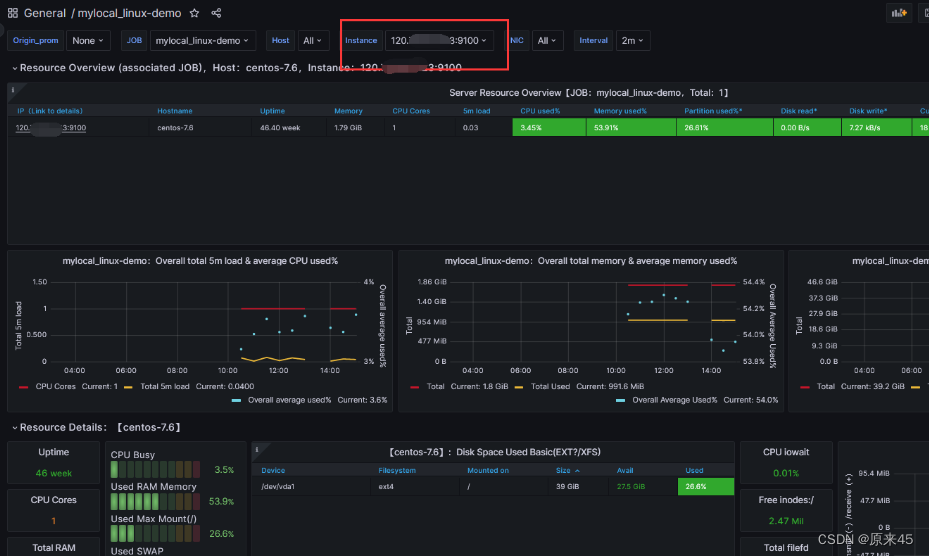
Prometheus - Grafana 监控 MySQLD Linux服务器 demo版
目录 首先是下载Prometheus 下载和安装 配置Prometheus 查看监控数据 监控mysql demo 部署 mysqld_exporter 组件 配置 Prometheus 获取监控数据 -------------------------------------- 安装和使用Grafana 启动Grafana -------------------------------------- 配…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
