代码随想录算法训练营第四十三天-动态规划5|1049. 最后一块石头的重量 II , 494. 目标和 , 474.一和零
最后一块石头重量转化为将一个集合分隔成两个集合,两个集合之间的差值最小,就是最后剩下最小的石头重量。这里可以求集合的一个平均值,如果正好等于平均值,说明可以抵消,这时候重量为0,如果不行,就把这个平均值作为背包的容量,往这里面放东西,当放的重量最接近这个背包重量时,就是最优解。dp[i][j]表示背包的重量,也就是价值,i表示第i个石头,j表示背包的容量。最后用一个res来表示背包和平均值之间的最小差值。
目标和将数组集合分成两个子集,一个表示加号,一个表示减号。利用关系add(加号中的数字和) + diff(减号的数字和) = sum(整个集合的和)以及add - diff = target,推导出add = (target + sum) / 2;不满足这个关系就说明上式不成立,也就是不能分成满足条件的两份。dp[i][j] 表示放入的方法,i表示集合中的第i个数,j表示现在背包容量,也就是add。最后的dp[nums.length ][add]就是nums集合中添加add个数的最多方法。
一和零,dp[i][j] 表示的是放入的最大子集的个数,i表示0的容量,j表示1的容量。有点像双背包,需要往这两个背包里面装东西。而加一个外循环k来挨个遍历物品strs。
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示:
1 <= stones.length <= 30
1 <= stones[i] <= 100
class Solution {public int lastStoneWeightII(int[] stones) {int len = stones.length;if(len == 1){return stones[0];}int sum = 0;for(int wight : stones){sum += wight;}int target = sum / 2 ;//这里加1个k主要是当sum是奇数时,那么最后的重量差要加上这个修正值。//比如说stones = [2,7,4,1,8,1],那么sum = 23,算出来target = 11;//如果最后背包和这个target的差值=0;那么最后剩下的重量就是1,也就是修正值//如果背包和这个target的差值=2;那么剩下的重量就是2 * 2 + 1;也就是2倍的差值加上修正值。//因为差值为2时,一个背包为9,剩下为14(13 + 1),差值就是5.int k = sum % 2;int res = sum;int[][] dp = new int [len][target + 1];for(int i = 0; i < len; i++){dp[i][0] = 0;}for(int j = 0; j <= target; j++){if(j >= stones[0]){dp[0][j] = stones[0];}}for(int i = 1; i < len; i++){for(int j = 1; j <= target; j++){if(j >= stones[i]){dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);}else{dp[i][j] = dp[i - 1][j];} }res = Math.min(res, target - dp[i][target]);}// for (int i = 0; i < len; i++) {// for (int j = 0; j <= target; j++) {// System.out.print(dp[i][j]+" ");// }// System.out.println();// }return 2 * res + k;//这是另外一种输出,也就不用计算修正值和比较背包之间差值的最小值,直接计算背包容量//装的最大的石头重量,然后剩余的重量减去背包的重量就是差值。//return (sum - dp[stones.length - 1][target]) - dp[stones.length - 1][target];}
}494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for(int n : nums){sum += n;}int add = 0;int diff = 0;add = (target + sum) / 2;//如果和是奇数,那肯定是不能得到合适的式子if((target + sum) % 2 != 0 || add < 0){return 0;}int [][] dp = new int[nums.length + 1][add + 1];dp[0][0] = 1;for(int i = 1; i <= nums.length; i++){for(int j = 0; j <= add; j++){if(j >= nums[i - 1]){dp[i][j] = dp[i - 1][j - nums[i - 1]] + dp[i - 1][j];}else{dp[i][j] = dp[i - 1][j];}}}return dp[nums.length ][add];}
}474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 '0' 和 '1' 组成
1 <= m, n <= 100
class Solution {public int findMaxForm(String[] strs, int m, int n) {int len = strs.length;int[] zero = new int[len];int[] one = new int[len];for(int i = 0; i < len; i++){for(int j = 0; j < strs[i].length(); j++){if(strs[i].charAt(j) == '0'){zero[i] ++;}else{one[i]++;}} }int[][] dp = new int[m + 1][n + 1];for(int k = 0; k < len; k++){for(int i = m; i >= zero[k]; i--){for(int j = n; j >= one[k]; j--){dp[i][j] = Math.max(dp[i][j], dp[i - zero[k]][j - one[k]] + 1);}}}return dp[m][n];}
}相关文章:

代码随想录算法训练营第四十三天-动态规划5|1049. 最后一块石头的重量 II , 494. 目标和 , 474.一和零
最后一块石头重量转化为将一个集合分隔成两个集合,两个集合之间的差值最小,就是最后剩下最小的石头重量。这里可以求集合的一个平均值,如果正好等于平均值,说明可以抵消,这时候重量为0,如果不行,…...

《淘宝网店》:计算总收益
目录 一、题目 二、思路 1、当两个年份不一样的时候 (1)from年剩余之后的收益 (2)中间年份的全部收益 (3)to年有的收益 2、同一个年份 三、代码 详细注释版本: 简化注释版本ÿ…...

2023年03月青少年软件编程C语言一级真题答案——持续更新.....
1.字符长方形 给定一个字符,用它构造一个长为4个字符,宽为3个字符的长方形,可以参考样例输出。 时间限制:1000 内存限制:65536 输入 输入只有一行, 包含一个字符。 输出 该字符构成的长方形,长4个字符,宽3个字符。 样例输入 * 样例输出 **** **** ****#include<bi…...

家用洗地机好用吗?好用的洗地机分享
洗地机是一种高效、节能、环保的清洁设备,广泛应用于各种场所的地面清洁工作。它不仅可以快速清洁地面,还可以有效去除污渍、油渍等难以清洁的污染物,让地面恢复光洁如新的状态。同时,洗地机还可以减少清洁人员的劳动强度…...
《分解因数》:质因数分解
目录 一、题目: 二、思路: 三、代码: 一、题目: 分解因数 《分解因数》题目链接 所谓因子分解,就是把给定的正整数a,分解成若干个素数的乘积,即 a a1 a2 a3 ... an,并且 1 < a1…...
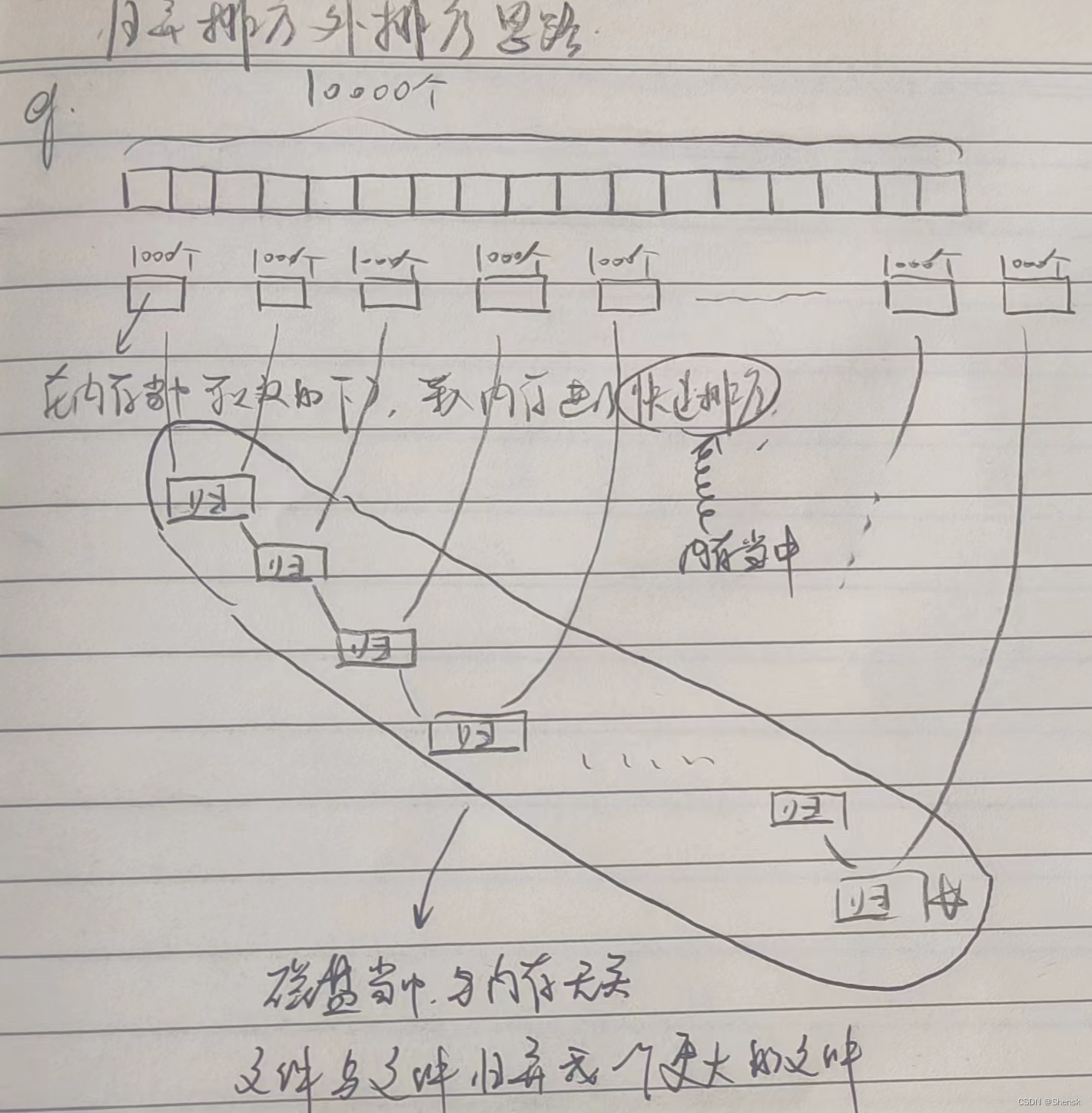
(排序10)归并排序的外排序应用(文件排序)
TIPS 在一些文件操作函数当中,fputc与fgetc这两个函数都是针对字符的,如果说你需要往文件里面去放入整形啊等等,不是字符的类型,这时候就用fprintf,fscanf在参数里面数据类型控制一下就可以。但是话说回来,…...
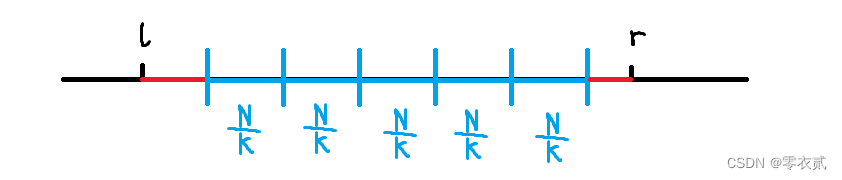
浅谈根号分治与分块
文章目录 1. 根号分治哈希冲突 2. 线性分块引入教主的魔法[CQOI2011] 动态逆序对[国家集训队] 排队[HNOI2010] 弹飞绵羊蒲公英 1. 根号分治 哈希冲突 题目1 n n n 个数, m m m 次操作。操作 1 为修改某一个数的值,操作 2 为查询所有满足下标模 x x x …...
(OpenAI)ChatGPT注册登录常见问题错误代码及其解决方法
在使用 ChatGPT 的时候我们可能会碰到一些错误的代码,本文统一来介绍一下每一种错误以及解决方法。 错误代码1. 不能在当前国家使用 出现场景:一般在注册或登录的时候会出现。 原因:主要是ChatGPT检测到当前访问所在的地区不允许访问导致。 …...
MySQL主从复制、读写分离(MayCat2)实现数据同步
文章目录 1.MySQL主从复制原理。2.实现MySQL主从复制(一主两从)。3.基于MySQL一主两从配置,完成MySQL读写分离配置。(MyCat2) 1.MySQL主从复制原理。 MySQL主从复制是一个异步的复制过程,底层是基于Mysql数…...

Linux 云服务器好用吗?(解读Linux云服务器的特点优势)
如今,云计算越来越受欢迎,许多公司正在将业务转移到那里。企业向云过渡的主要原因是它提供的众多服务,包括安全和充足的存储、数据库、服务器和其他关键元素。 作为相对前|沿的技术之一,云建立在虚拟服务器上。Linux 服务器…...
研读Rust圣经解析——Rust learn-8(match,if-let简洁控制流,包管理)
研读Rust圣经解析——Rust learn-8(match,if-let简洁控制流,包管理) matchother和占位符_区别 easy matchenum matchno valuematch inner Option matchmore better way if-let整洁控制包管理模块(mod)拆分声明modpub公开use展开引用拆解模块结…...

G8期刊《全体育》期刊简介及投稿要求
G8期刊《全体育》期刊简介及投稿要求 《全体育》是由湖南体育产业集团有限公司主管、体坛传媒集团股份有限公司主办、中教体育 出版发行的体育综合性期刊。 主管:湖南体育产业集团有限公司 主办:体坛传媒集团股份有限公司 国内刊号:CN4…...
数据结构和算法学习记录——层序遍历(层次遍历)、二叉树遍历的应用(输出二叉树中的叶节点、求二叉树的高度、二元运算表达式树及其遍历、由两种遍历序列确定二叉树)
目录 层序遍历 思路图解 代码实现 二叉树遍历的应用 输出二叉树中的叶节点 代码实现 求二叉树的高度 思路图解 代码实现 二元运算表达式树及其遍历 由两种遍历序列确定二叉树 层序遍历 层序遍历可以通过一个队列来实现,其基本过程为: 先根…...
、查询、删除数据库等操作解析(Cypher语句))
【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除数据库等操作解析(Cypher语句)
【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除操作解析(Cypher语句) 文章目录 【Neo4j数据库】图数据库_Neo4j增加节点(关系)、查询、删除操作解析(Cypher语句)1. 介绍2…...
命令)
Linux移动文件和文件夹(目录)命令
命令mv 英文move 翻译移动 mv命令可以移动文件或文件夹(目录),也可以重命令(覆盖)文件。 1. 移动文件/重命名 单纯地移动某一个文件直接使用: mv <源文件名称/地址> <新文件名称/地址>这个方法…...

Pandas的应用-5
Pandas是一个强大的数据处理库,它提供了高性能、易于使用的数据结构和数据分析工具。本文将介绍Pandas常用的数据结构和常用的数据分析技术,包括DataFrame的应用、窗口计算、相关性判定、Index的应用、范围索引、分类索引、多级索引以及日期时间索引。 …...

java继承类怎么写
继承类是通过把父类的方法和属性继承到一个类中,而子类的方法和属性是子类自己定义的。 Java中有一个很重要的概念叫做继承,这也是 Java语言的精髓所在。Java语言提供了一种机制,叫做派生类。在 Java中,如果没有实现了某个派生类方…...

面向对象程序设计
OOP 【面向对象程序设计】(OOP)与【面向过程程序设计】在思维方式上存在着很大的差别。【面向过程程序设计】中,算法是第一位的,数据结构是第二位的,这就明确地表述了程序员的工作方式。首先要确定如何操作数据&#…...
)
Linux 用户身份切换(su,sudo)
文章目录 Linux 用户身份切换su使用案例 sudo使用案例 visudo与/etc/sudoers单一用户可使用root所有命令,与sudoers文件语法利用wheel用户组以免密码的功能处理visudo有限制的命令操作通过别名创建visudosudo的时间间隔问题sudo搭配su的使用方式 Linux 用户身份切换…...

求倒置数问题
文章目录 求倒置数程序设计程序分析求倒置数 【问题描述】数组A【0,…,n-1】是一个n个不同整数数构成的数组。如果i<j,但是A[i]〉A[j],则这对元素(A[i],A[j])被称为一个倒置(inversion)。设计一个O(nlogn)算法来计算数组中的倒置数量 【输入形式】输入两行,第一行…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

WEB3全栈开发——面试专业技能点P8DevOps / 区块链部署
一、Hardhat / Foundry 进行合约部署 概念介绍 Hardhat 和 Foundry 都是以太坊智能合约开发的工具套件,支持合约的编译、测试和部署。 它们允许开发者在本地或测试网络快速开发智能合约,并部署到链上(测试网或主网)。 部署过程…...

OCC笔记:TDF_Label中有多个相同类型属性
注:OCCT版本:7.9.1 TDF_Label中有多个相同类型的属性的方案 OCAF imposes the restriction that only one attribute type may be allocated to one label. It is necessary to take into account the design of the application data tree. For exampl…...

开源项目实战学习之YOLO11:12.6 ultralytics-models-tiny_encoder.py
👉 欢迎关注,了解更多精彩内容 👉 欢迎关注,了解更多精彩内容 👉 欢迎关注,了解更多精彩内容 ultralytics-models-sam 1.sam-modules-tiny_encoder.py2.数据处理流程3.代码架构图(类层次与依赖)blocks.py: 定义模型中的各种模块结构 ,如卷积块、残差块等基础构建…...
