Docker网络案例
bridge
是什么
Docker 服务默认会创建一个 docker0 网桥(其上有一个 docker0 内部接口),该桥接网络的名称为docker0,它在内核层连通了其他的物理或虚拟网卡,这就将所有容器和本地主机都放到同一个物理网络。Docker 默认指定了 docker0 接口 的 IP 地址和子网掩码,让主机和容器之间可以通过网桥相互通信。
# 查看 bridge 网络的详细信息,并通过 grep 获取名称项
docker network inspect bridge | grep name

ifconfig

案例
说明
1 Docker使用Linux桥接,在宿主机虚拟一个Docker容器网桥(docker0),Docker启动一个容器时会根据Docker网桥的网段分配给容器一个IP地址,称为Container-IP,同时Docker网桥是每个容器的默认网关。因为在同一宿主机内的容器都接入同一个网桥,这样容器之间就能够通过容器的Container-IP直接通信。
2 docker run 的时候,没有指定network的话默认使用的网桥模式就是bridge,使用的就是docker0。在宿主机ifconfig,就可以看到docker0和自己create的network(后面讲)eth0,eth1
相关文章:

Docker网络案例
bridge 是什么 Docker 服务默认会创建一个 docker0 网桥(其上有一个 docker0 内部接口),该桥接网络的名称为docker0,它在内核层连通了其他的物理或虚拟网卡,这就将所有容器和本地主机都放到同一个物理网络。Docker 默认指定了 docker0 接口 的 IP 地址和子网掩码,让主机…...
Java实验课的学习笔记(二)类的简单使用
本文章就讲的是很基础的类的使用 重点大概就是类的构造函数以及一些很基础的东西。 实验内容是些老生常谈的东西,Complex类,在当初学C面向对象的时候也是这个样子展开的。 内容如以下: public class Complex {float real;float imag;public…...

实战案例|聚焦攻击面管理,腾讯安全威胁情报守护头部券商资产安全
金融“活水”润泽千行百业,对金融客户来说,由于业务场景存在特殊性和复杂性,网络安全必然是一场“持久战”。如何在事前做好安全部署,构建威胁情报分析的防护体系至为重要,实现更为精准、高效的动态防御。 客户名片 …...

c++算法初级8——递推
c算法初级8——递推 文章目录 c算法初级8——递推递推递推思想的运用错位排序杨辉三角(二维递推) 递推 递推思想: 根据已有的东西一点点地推出未知的东西。 使用递推解题三步骤: 数学建模找出递推式和初始条件写出代码。 张爽…...
Java后端面试题 重难点和被问到没答上来的点(包括java基础、关系型数据库、Redis、计算机网络、Spring、Java多线程、vue等)
以下是我记录的一些重点问题和面试中被问到没答上来的问题,包括java基础、关系型数据库、Redis、计算机网络、Spring、Java多线程、vue 问题目录 1.fail-safe和fail-fast2.四引用3.explain字段重要内容4.maven三大生命周期5.MYSQL 创建修改表6.数据库三范式7.Strin…...

易观千帆 | 2023年3月银行APP月活跃用户规模盘点
易观:2023年3月手机银行服务应用活跃人数53289.05万,环比增长2.15%,同比增长8.87%。 2023年3月信用卡服务应用活跃人数10800.71万,环比增长1.87%,同比增长18.64%。 2023年3月城商行手机银行服务应用活跃人数3827.43万&…...
[Android+JetPack] (Java实现) Retrofit2+RxJava3+Paging3+RecyclerView 实现加载网络数据例子 记录
文章目录 前言参考链接依赖库及版本Demo效果接口及数据展示各项模块Retrofit2Bean,对应上面的接口返回.Service API部分 Paging3PagingSource以及 RxPagingSourcePagingDataAdapter 适配器ViewModelPublicInfoPage /Activity 最后 前言 继续安卓学习之旅,本章的主要目标是: 1.完…...

Java 解析配置文件注入到配置类属性中供全局使用【开发记录】
1、背景:假设目前有两个接口,一个是查询快递订单状态的JSF接口,一个是查询快运订单状态的JSF接口,现有一个需求,要将这两个接口统一为一个入口,发布到物流开放平台供外界调用。 注意:以下代码均…...
【Python开发手册】深入剖析Google Python开发规范:规范Python注释写作
💖 作者简介:大家好,我是Zeeland,全栈领域优质创作者。📝 CSDN主页:Zeeland🔥📣 我的博客:Zeeland📚 Github主页: Undertone0809 (Zeeland) (github.com)&…...

Python入门教程+项目实战-9.3节: 字符串的操作方法
目录 9.3.1 字符串常用操作方法 9.3.2 获取字符串长度 9.3.3 字符串的大小写操作 9.3.4 删除字符串中的空白字符 9.3.5 字符串的子串查找 9.3.6 字符串的子串统计 9.3.7 字符串的子串替换 9.3.8 字符串的拆分函数 9.3.9 字符串的前缀与后缀9.3.10 知识要点 9.3.11 系…...
ENVI 5.6软件安装教程
软件下载 [软件名称]:ENVI 5.6 [软件大小]:3.25G [安装环境]:Win7~Win11或更高 软件介绍 ENVI 5.6是一款实现遥感图像处理的工具,已经广泛应用于科研、环境保护、气象、石油矿产勘探、农业、林业、医学、地球科学、公用设施管…...
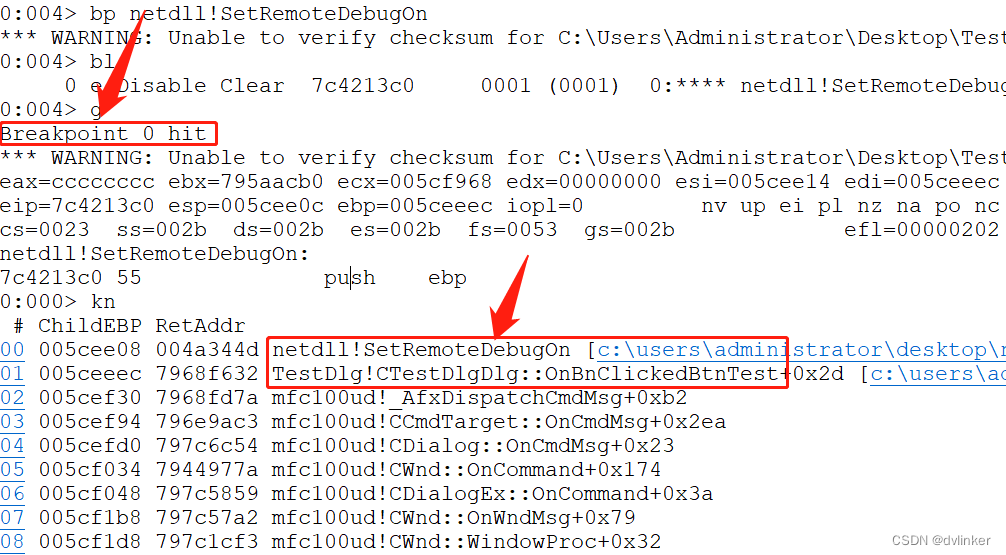
在Windbg中设置断点追踪打开C++程序远程调试开关的模块
目录 1、Windbg动态调试 2、在Windbg中设置断点 2.1、在函数入口处设置断点 2.2、在函数内部某一行上设置断点 3、设置断点跟踪对打开远程调试开关接口的调用 3.1、编写演示代码 3.2、在Windbg中设置调用SetRemoteDebugOn接口的断点进行跟踪 4、最后 VC常用功能开发汇总…...

CRM客户管理软件开发功能有哪些?
互联网技术的不断提高使得企业管理方式也发生了变化,企业CRM系统应用市场逐渐扩大,相关软件开发也引起越来越多商家企业的关注。因为企业CRM系统软件开发能够根据企业需求制作,帮助企业更好的追踪管理客户信息,实时更新并进行相关…...
)
C++函数式魔法之旅(Journey of Functional Magic)
C函数式魔法之旅(Journey of Functional Magic) 一、引言(Introduction)C Functional模板库简介(Overview of C Functional Template Library)Functional模板库的重要性和作用(The Importance a…...

Vue基础入门(上)
<script src"https://unpkg.com/vuenext"></script> 从面向dom编程到面向数据编程 输入显示列表 const appVue.createApp({data(){return{inputValue:,list:[]}},methods:{handleAddItem(){this.list.push(this.inputValue);this.inputValue;}},templ…...
字符串匹配—KMP算法
字符串匹配的应用非常广泛,例如在搜索引擎中,我们通过键入一些关键字就可以得到相关的搜索结果,搜索引擎在这个过程中就使用字符串匹配算法,它通过在资源中匹配关键字,最后给出符合条件的搜索结果。并且我们在使用计算…...
【微信小程序】 权限接口梳理以及代码实现
1、权限接口说明 官方权限说明 部分接口需要经过用户授权统一才能调用。我们把这些接口按使用范围分成多个scope,用户选择对scope进行授权,当授权给一个scope之后,其对应的所有接口都可以直接使用。 此类接口调用时: 如…...

【每日一词】leit-motif
1、释义 leit-motif: n. 主乐调;主题;主旨。 复数:leit-motifs 2、例句 Hence the ‘ancient’ rhyme that appears as the leit-motif of The Lord of the Rings, Three Rings for the Elven-Kings under the sky, Seven for the Dwarf-lor…...

windows 环境修改 Docker 存储目录
windows 环境修改存储目录 docker 安装时不提供指定安装路径和数据存储路径的选项,且默认是安装在C盘的。C盘比较小的,等docker运行久了,一大堆的东西放在上面容易导致磁盘爆掉。所以安装前可以做些准备,让安装的实际路径不在C盘&…...

上海市青少年算法月赛丙组—目录汇总
上海市青少年算法2023年3月月赛(丙组) T1 神奇的字母序列 T2 约数的分类 T3 循环播放 T4 数对的个数 T5 选取子段 上海市青少年算法2023年2月月赛(丙组) T1 格式改写 T2 倍数统计 T3 区间的并 T4 平分数字(一…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
