C++算法恢复训练之快速排序
快速排序(Quick Sort)是一种基于分治思想的排序算法,它通过将待排序数组分成两个子数组,其中一个子数组的所有元素都比另一个子数组的元素小,然后对这两个子数组递归地进行排序,最终将整个数组排序。快速排序是一种原地排序算法,其时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
下面是使用 C++ 实现的 经典 快速排序算法:
#include <vector>
#include <iostream>
using namespace std;int partitionSimple(vector<int>& array, int left, int right)
{if (left >= right){return -1;}// Use the value of index `right` as the pivotconst int pivot = array[right];int lessBound = left - 1;for (int i = left; i < right; i++){// If the current element is not more than then pivot value,// then swap it with the less part's next value, and make the less part add 1if (array[i] <= pivot){swap(array[i], array[++lessBound]);}}// At last, swap the pivot with the next element of less partswap(array[lessBound + 1], array[right]);return lessBound + 1;
}void quickSortSimple(vector<int>& array, int left, int right)
{if (left >= right){return;}const int pivotIndex = partitionSimple(array, left, right);quickSortSimple(array, left, pivotIndex - 1);quickSortSimple(array, pivotIndex + 1, right);
}void quickSort(vector<int>& array)
{quickSortSimple(array, 0, array.size() - 1);
}
经典快速排序的实现过程可以分为两个步骤:
- 分割子问题:选取一个元素作为基准值(
pivot),将待排序数组分成两个子数组,一个子数组中的元素都小于等于基准值,另一个子数组中的元素都大于等于基准值。 - 合并解决方案:对两个子数组分别进行快速排序(递归),最后将两个已排序的子数组合并成一个有序数组。
递归的部分其实比较好理解和实现,那么现在可以将问题简化为:给定一个数组,和一个基准值,如何将小于等于基准值的元素放在数组左边,将大于基准值的元素放在数组右边?
我的实现思路是利用一个小于等于pivot值的边界的索引这样一个概念变量,对应代码中的lessBound,它对应的元素及其左边部分都小于等于pivot值。在随后的数组遍历过程中,如果遍历的元素满足这样的条件,则将该元素与lessbound的后一位对调,然后将lessbound的范围扩大一位。核心思路类似快慢指针:即lessbound扮演的是慢指针,i扮演的是快指针。
最后,数组已经被分成了两个子数组,其中一个子数组中的元素都小于等于基准值,另一个子数组中的元素都大于基准值。然后分别对这两个子数组进行递归。
快速排序的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),其中 n n n 是待排序数组的长度。快速排序每次将待排序数组分成两个子数组,其中一个子数组中的元素都小于等于基准值,另一个子数组中的元素都大于等于基准值。
由于快速排序每次都将待排序数组分成两个子数组,因此递归树的高度为 l o g n logn logn。每个节点所处理的子问题的规模最大为 n n n,因此快速排序的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
需要注意的是,在最坏情况下,快速排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2),此时待排序数组已经有序或者接近有序,且每次选取的基准值都是数组中的最小或最大元素。为了避免最坏情况的发生,可以采用以下优化措施:
- 随机选取基准值。
- 三数取中法(Median-of-three partitioning):从子数组的左端、右端和中间位置分别选取一个元素,选择它们的中间值作为基准值。
除此以外,从算法本身出发,经典快排是利用某个值作为基准值,其算法实质在于一个周期内确定这个pivot的下标索引。从这点考虑,可以考虑在这个周期内将所有与pivot相等的值的位置都敲定,在递归时就不考虑这一批数。
C++相应的实现:
vector<int> partitionOptimized(vector<int>& array, int left, int right)
{if (left >= right){return {-1, -1};}int pivot = array[right];int lessBound = left - 1, moreBound = right;int i = left;while (i < moreBound){if (array[i] == pivot){i++;}else if (array[i] < pivot){swap(array[++lessBound], array[i++]);}else{// array[i] > pivotswap(array[--moreBound], array[i]);}}swap(array[right], array[moreBound++]);return {lessBound, moreBound};
}void quickSortOptimized(vector<int>& array, int left, int right)
{if (left >= right){return;}vector<int> bounds = partitionOptimized(array, left, right);quickSortOptimized(array, left, bounds[0]);quickSortOptimized(array, bounds[1], right);
}void quickSort(vector<int>& array)
{quickSortOptimized(array, 0, array.size() - 1);
}
新的算法的最显著的不同之处在于,partition的返回值是一个数组,保存了小于pivot的边界和大于pivot的边界,他们也是新一轮递归的依据。在计算这两个边界时(partition内),需要将一个数组拆分为:小于pivot的部分,等于pivot的部分,以及大于pivot的部分。此时主要是利用三个指针,分别指向小于pivot的部分的边界,大于pivot的部分的边界,以及当前遍历元素。如果当前元素小于pivot,则与之前的思路类似,将当前元素与小于边界的下一位调换,小于的边界扩大一位,继续下一个元素遍历;如果当前元素等于pivot,继续下一个元素遍历,其他不变;如果当前元素大于pivot,则需要将当前元素与大于边界的下一位进行调换,大于的边界减小一位,注意此时仍然需要调查被调换元素的大小,即不继续一个元素的遍历。
当然,虽说是优化,但是这个思路也仅仅是在数组中有重复元素时会比经典快排稍微快一些,本质上算法复杂度并没有发生改变,也没有改变快排依赖数组状况的问题。
利用随机取基准值的方法确实可以令这个问题得到改善,但是取随机数本身也是需要一定的指令,其产生的消耗也是一个需要考虑和权衡的问题。
相关文章:

C++算法恢复训练之快速排序
快速排序(Quick Sort)是一种基于分治思想的排序算法,它通过将待排序数组分成两个子数组,其中一个子数组的所有元素都比另一个子数组的元素小,然后对这两个子数组递归地进行排序,最终将整个数组排序。快速排…...

事务的特性
四大特性 原子性(atomicity) 事务的一系列操作,要么所有操作所有都成功,要么一个操作都不做 一致性(consistency) 指数据的规则,在事务前/后应保持一致,事务的原子性保证了一致性 隔离性&a…...

Python 计算三角形的面积、Python 阶乘实例
Python 计算三角形的面积 以下实例为通过用户输入三角形三边长度,并计算三角形的面积: # -*- coding: UTF-8 -*-# Filename : test.py # author by : www.w3cschool.cna float(input(输入三角形第一边长: )) b float(input(输入三角形第二边长: )) c …...

C++入门教程||C++ 重载运算符和重载函数||C++ 多态
C 重载运算符和重载函数 C 重载运算符和重载函数 C 允许在同一作用域中的某个函数和运算符指定多个定义,分别称为函数重载和运算符重载。 重载声明是指一个与之前已经在该作用域内声明过的函数或方法具有相同名称的声明,但是它们的参数列表和定义&…...
docker+docker-compose+nginx前后端分离项目部署
文章目录 1.安装docker1.1 基于centos的安装1.2 基于ubuntu 2.配置国内加速器2.1 配置阿里云加速器🍀 找到相应页面🍀 创建 docker 目录🍀 创建 daemon.json 文件🍀 重新加载服务配置文件🍀 重启 docker 引擎 2.2 配置…...
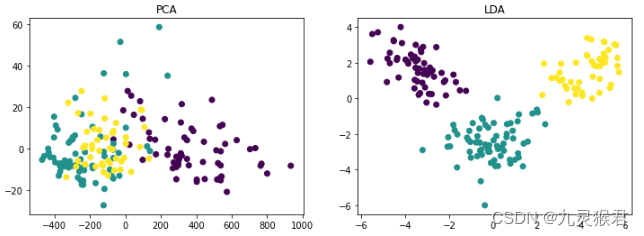
基于PCA与LDA的数据降维实践
基于PCA与LDA的数据降维实践 描述 数据降维(Dimension Reduction)是降低数据冗余、消除噪音数据的干扰、提取有效特征、提升模型的效率和准确性的有效途径, PCA(主成分分析)和LDA(线性判别分析࿰…...

【Hello Network】网络编程套接字(一)
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:简单介绍网络的基础概念 网络编程套接字(一) 预备知识源ip和目的ip端口号TCP和UDP协议网络中的字节序 socket编程接口socket常…...
【计算机网络】学习笔记:第二章 物理层(五千字详细配图)【王道考研】
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...
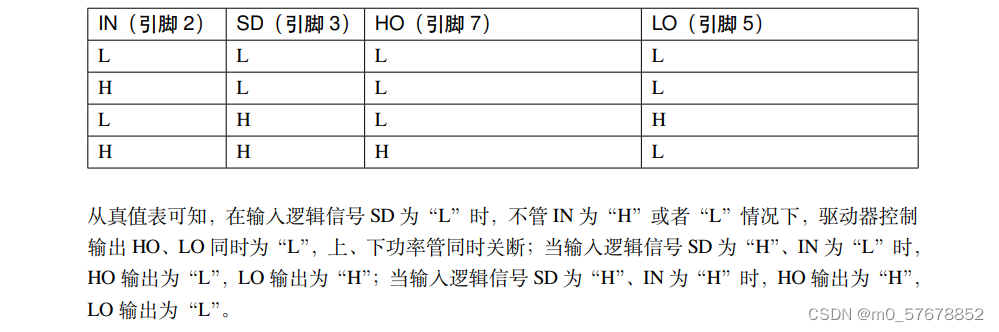
直流有刷电机的电路分析
这里写目录标题 H桥改进后的电路L298N原理图野火的电机驱动板MOS管野火的原理图 H桥 当 Q1 和 Q4 导通时,电流将经过 Q1 从左往右流过电机,在经过 Q4 流到电源负极,这时图中电机可以顺时针转动。 当 Q3 和 Q2 导通时,电流将经过 Q…...
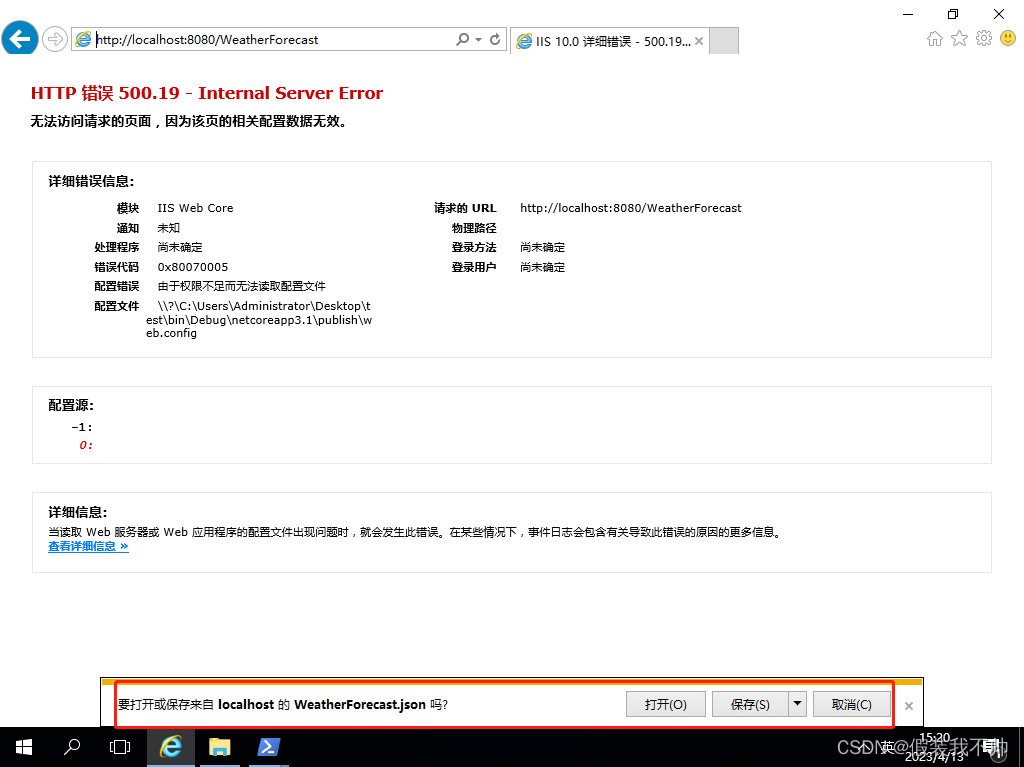
使用PowerShell自动部署ASP.NetCore程序到IIS
asp.net core 安装asp.net core sdk https://dotnet.microsoft.com/en-us/download/dotnet/3.1 创建asp.net core项目 dotnet new webapi运行项目 访问https://localhost:5001/WeatherForecast iis配置 安装iis 以管理员身份运行powershell Enable-WindowsOptiona…...
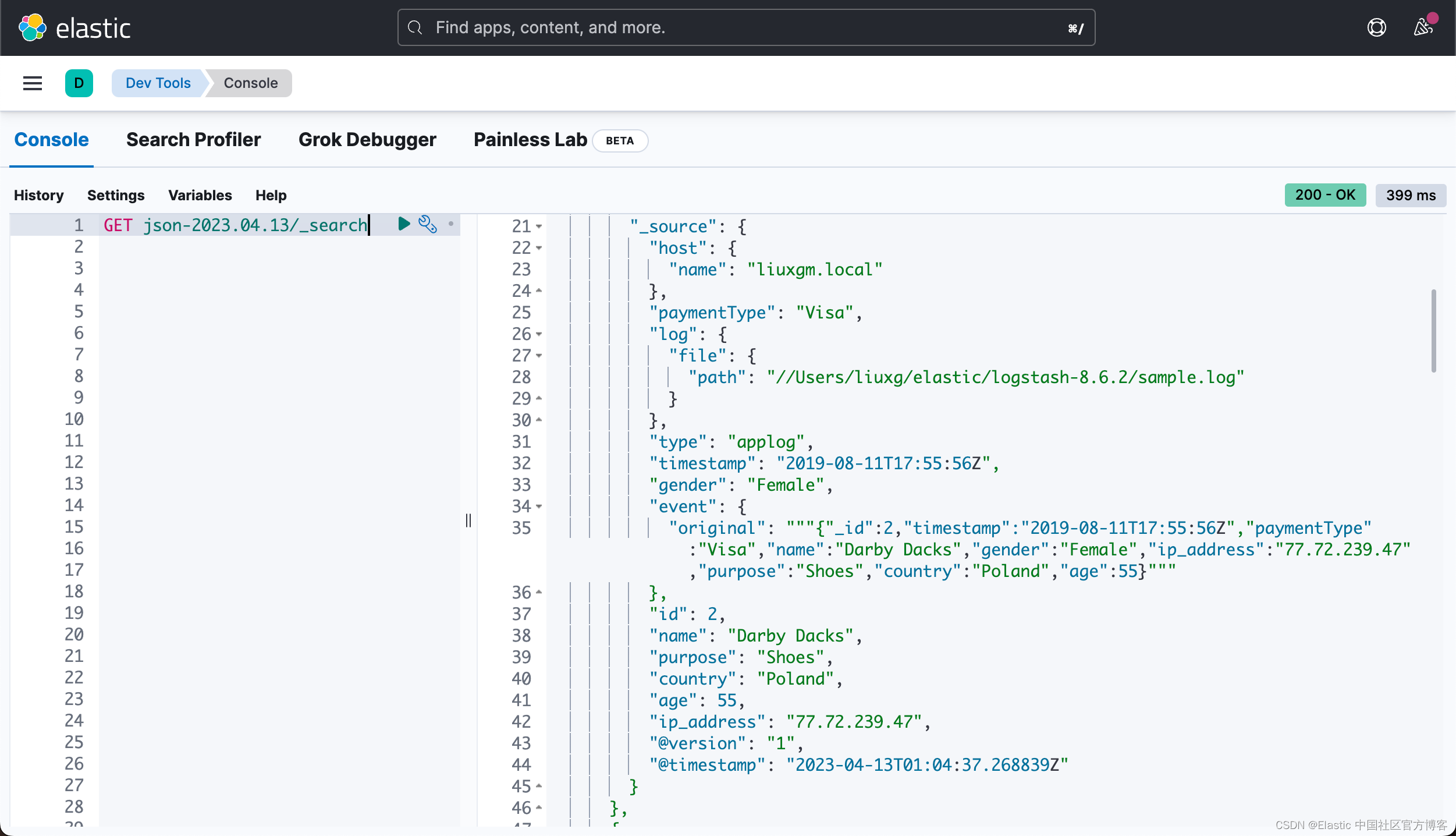
Elasticsearch:保留字段名称
作为 Elasticsearch 用户,我们从许多不同的位置收集数据。 我们使用 Logstash、Beats 和其他工具来抓取数据并将它们发送到 Elasticsearch。 有时,我们无法控制数据本身,我们需要管理数据的结构,甚至需要在摄取数据时处理字段名称…...
解密:迈向 Qt 网络编程之巅)
Qt 套接字类(QTcpSocket和QUdpSocket)解密:迈向 Qt 网络编程之巅
Qt 套接字类解密:迈向 Qt 网络编程之巅 一、套接字类简介(Introduction to Socket Classes)# 套接字类的作用(Role of Socket Classes)Qt 中常见套接字类概述(Overview of Common Socket Classes in Qt&…...

Python视频编辑库:MoviePy
MoviePy MoviePy是一个关于视频编辑的python库,主要包括:剪辑,嵌入拼接,标题插入,视频合成(又名非线性编辑),视频处理,和自定制效果。可以看gallery中的一些实例来了解用法。MoviePy可以读写所有的音频和视频格式,包括GIF,通过python2.7+和python3可以跨平台运行于window/M…...

课程3:ASP.NET Core 身份验证 - Cookie
课程简介目录 🚀前言一、.Net Core 身份验证简介二、开启Cookie身份验证三、添加登录接口3.1 添加登录Dto3.2 添加登录接口Login3.3 获取用户信息接口,添加身份验证四、获取用户信息接口测试4.1 测试获取用户信息接口4.2 登录4.3 再次测试:获取用户信息接口4.4 其他浏览器测…...

Visual Studio 2022如何安装和使用MSDN
我是荔园微风,作为一名在IT界整整25年的老兵,在后台收到提问,问我Visual Studio 2022如何安装和使用MSDN,这个我之前也没有在这个版本上装过MSDN,我之前是在Visual Studio 2017版上装过MSDN,那既然有人问了…...

82.qt qml-2D粒子系统、粒子方向、粒子项(一)
由于粒子系统相关的类比较多, 所以本章参考自QmlBook in chinese的粒子章节配合学习: 由于QmlBook in chinese翻译过来的文字有些比较难理解,所以本章在它的基础上做些个人理解,建议学习的小伙伴最好配合QmlBook in chinese一起学习。 1.介绍 粒子模拟的核心是粒子系统(Partic…...

引用的底层原理(汇编指令),引用与指针的联系与区别
TIPS 2. 3. 4. 引用的底层本质 在语法层面上的话,这个引用是不开空间的,相当于是对一个变量进行一个取别名的这么一个操作。在底层实现上实际是有空间的,因为引用是按照指针方式来实现的。然而如果你从底层的角度去看的话,因…...

磁盘的移臂调度算法
1、概要 访问磁盘,首先要找到数据,但机械硬盘并不是直接电子读取,是需要移动磁头到相应的数据块上才能读取的,即需要磁头移动到目标柱面(磁道),然后磁片旋转使磁头能访问到相应扇区,进而读取到数据。 根据访…...
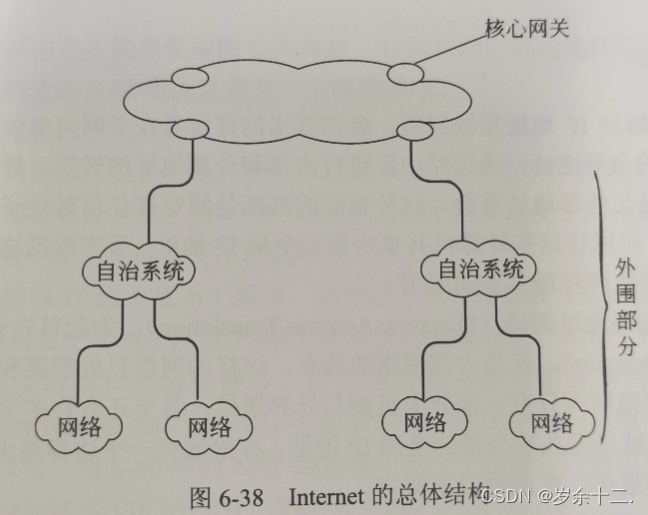
软考第六章 网络互连与互联网
网络互连与互联网 1.网络互连设备 组成因特网的各个网络叫做子网,用于连接子网的设备叫做中间系统。它的主要作用是协调各个网络的工作,使得跨网络的通信得以实现。 网络互连设备可以根据它们工作的协议层进行分类: 中继器:工…...

C6678-缓存和内存
C6678-缓存和内存 全局内存映射扩展内存控制器(XMC)-MPAX内存保护与地址扩展使用例程缓存 全局内存映射 扩展内存控制器(XMC)-MPAX内存保护与地址扩展 每个C66x核心都具有相同大小的L1和L2缓存,并且可配置为普通内存使…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
