基于PCA与LDA的数据降维实践
基于PCA与LDA的数据降维实践
描述
数据降维(Dimension Reduction)是降低数据冗余、消除噪音数据的干扰、提取有效特征、提升模型的效率和准确性的有效途径, PCA(主成分分析)和LDA(线性判别分析)是机器学习和数据分析中两种常用的经典降维算法。
本任务通过两个降维案例熟悉PCA和LDA降维的原理、区别及调用方法。
源码下载
环境
-
操作系统:Windows 10、Ubuntu18.04
-
工具软件:Anaconda3 2019、Python3.7
-
硬件环境:无特殊要求
-
依赖库列表
matplotlib 3.3.4 scikit-learn 0.24.2
分析
任务1、基于PCA算法实现鸢尾花数据集降维,涉及下列三个环节:
A)加载鸢尾花(Iris)数据并进行降维
B)降维后的数据可视化
C)使用K-NN算法进行分类,对比降维前后的分类准确性
任务2、基于LDA算法实现红酒数据集降维,涉及以下四个环节:
A)加载红酒数据集
B)使用PCA和LDA两种算法对数据进行降维
C)降维结果可视化
D)降维前后的分类准确性对比
实施
1、基于PCA算法实现鸢尾花数据集降维
鸢尾花数据原有四个特征维度,运用PCA算法将特征维度降为两个,之后进行可视化并运用K-NN算法进行分类,对比降维前后的分类准确性(数据降维的目的之一是提升模型的准确性)。
1.1 加载鸢尾花特征数据,并使用PCA算法降维
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier# 加载鸢尾花数据集
iris= load_iris()
data = iris.data # 特征数据
target = iris.target # 标签数据
print(data.shape) # 查看数据维度(150, 4)# PCA降维
pca = PCA(n_components = 2).fit(data) # 利用PCA算法降成2维
new_data = pca.transform(data)
print(new_data.shape) # 查看数据维度(150,2)
结果如下:
(150, 4)
(150, 2)
可以看到,鸢尾花数据由四维(四个特征)降为两维度。
1.2 数据可视化,并使用K-NN算法对比降维前后的分类准确性
# 降维后的数据集可视化
plt.title('Iris dimensions reduction: 4 to 2')
plt.scatter(new_data[:, 0], new_data[:, 1], c=target)
plt.show()# 使用KNN算法对比降维前后分类的准确性
model = KNeighborsClassifier(3)
score = model.fit(data, target).score(data, target)
print('4-dims:', score)
score = model.fit(new_data, target).score(new_data, target)
print('2-dims:', score)
输出结果:
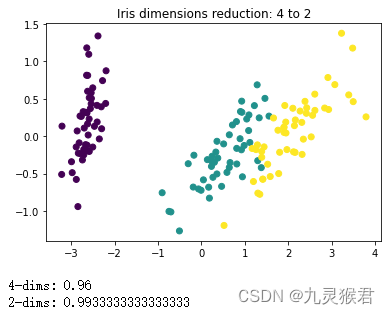
结果分析:
数据从4维降到2维后,可以很方便地进行可视化。从散点图中直观地看,降维后的数据较好地保留了原数据的分布信息。另外可以看到,降维后的KNN分类模型准确性有所提升,这也是数据降维的目的之一。
2、基于LDA算法实现红酒数据集降维
红酒数据集(Wine)有13个特征(即13个维度),我们分别使用PCA和LDA算法对数据集进行降维(降成2维),之后使用逻辑回归(LogisticRegression)分别在LDA算法降维前后的数据集上建立分类模型,对比同一种模型在数据集降维前后的准确性,直观感受数据降维对模型准确性的影响。
2.1 加载红酒数据集
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import load_wine# 加载红酒数据集
wine= load_wine()
data = wine.data
target = wine.target
print(data.shape) # 查看数据维度
2.2 分别使用LDA和PCA算法进行降维
# PCA降维(无类别)
pca = PCA(n_components = 2).fit(data) # 利用PCA算法降成2维
data_pca = pca.transform(data) # 降维转换
print('PCA:', data_pca.shape) # 查看数据维度# LDA降维(有类别,考虑样本标签)
lda = LinearDiscriminantAnalysis(n_components=2).fit(data, target)
data_lda = lda.transform(data)
print('LDA:', data_lda.shape)
结果如下:
(178, 13)
PCA: (178, 2)
LDA: (178, 2)
可以看到,两种算法都将红酒数据集由13维降成2维。
2.3 降维结果可视化
数据降到2维后,可以很方便地用散点图进行可视化,下面分别将两种算法降维后的红酒数据集进行可视化,对比其分布情况。
# LDA算法更适合有标签数据的降维
# 下面将两种方法降维后的数据进行可视化
fig = plt.figure(figsize=(12, 4)) # 生成画板# PCA降维结果
ax1 = fig.add_subplot(1, 2, 1) # 添加子图1
ax1.set_title('PCA')
ax1.scatter(data_pca[:, 0], data_pca[:, 1], c=target)# LDA降维结果
ax2 = fig.add_subplot(1, 2, 2) # 添加子图2
ax2.set_title('LDA')
ax2.scatter(data_lda[:, 0], data_lda[:, 1], c=target)plt.show() # 显示图像
显示结果:
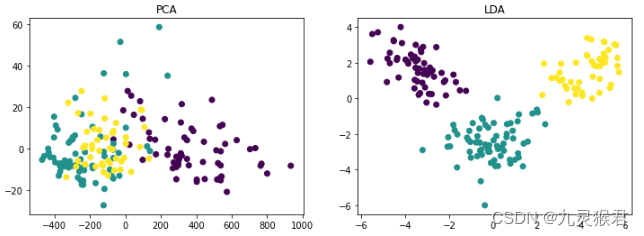
可以看到,LDA降维因为考虑到了样本的类别标签信息,降维后的数据分布能够较好地将类型分开。
2.4 LDA降维前后的分类准确性对比
使用逻辑回归算法,对LDA降维前后的数据集建立分类模型,对比其准确性。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression# 1、使用逻辑回归模型,在降维前的数据集上训练并评估
X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=0)model = LogisticRegression().fit(X_train, y_train)
score = model.score(X_test, y_test) # 在测试集上评估分类准确性
print(score)# 2、在LDA降维后的数据集上训练并评估
X_train, X_test, y_train, y_test = train_test_split(data_lda, target, random_state=0)
model = LogisticRegression().fit(X_train, y_train)
score = model.score(X_test, y_test) # 在测试集上评估分类准确性
print(score)
结果如下:
0.9333333333333333
1.0
可以看到,使用LDA降维后的数据建模,分类准确性有所提升。
相关文章:

基于PCA与LDA的数据降维实践
基于PCA与LDA的数据降维实践 描述 数据降维(Dimension Reduction)是降低数据冗余、消除噪音数据的干扰、提取有效特征、提升模型的效率和准确性的有效途径, PCA(主成分分析)和LDA(线性判别分析࿰…...

【Hello Network】网络编程套接字(一)
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:简单介绍网络的基础概念 网络编程套接字(一) 预备知识源ip和目的ip端口号TCP和UDP协议网络中的字节序 socket编程接口socket常…...
【计算机网络】学习笔记:第二章 物理层(五千字详细配图)【王道考研】
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...
直流有刷电机的电路分析
这里写目录标题 H桥改进后的电路L298N原理图野火的电机驱动板MOS管野火的原理图 H桥 当 Q1 和 Q4 导通时,电流将经过 Q1 从左往右流过电机,在经过 Q4 流到电源负极,这时图中电机可以顺时针转动。 当 Q3 和 Q2 导通时,电流将经过 Q…...
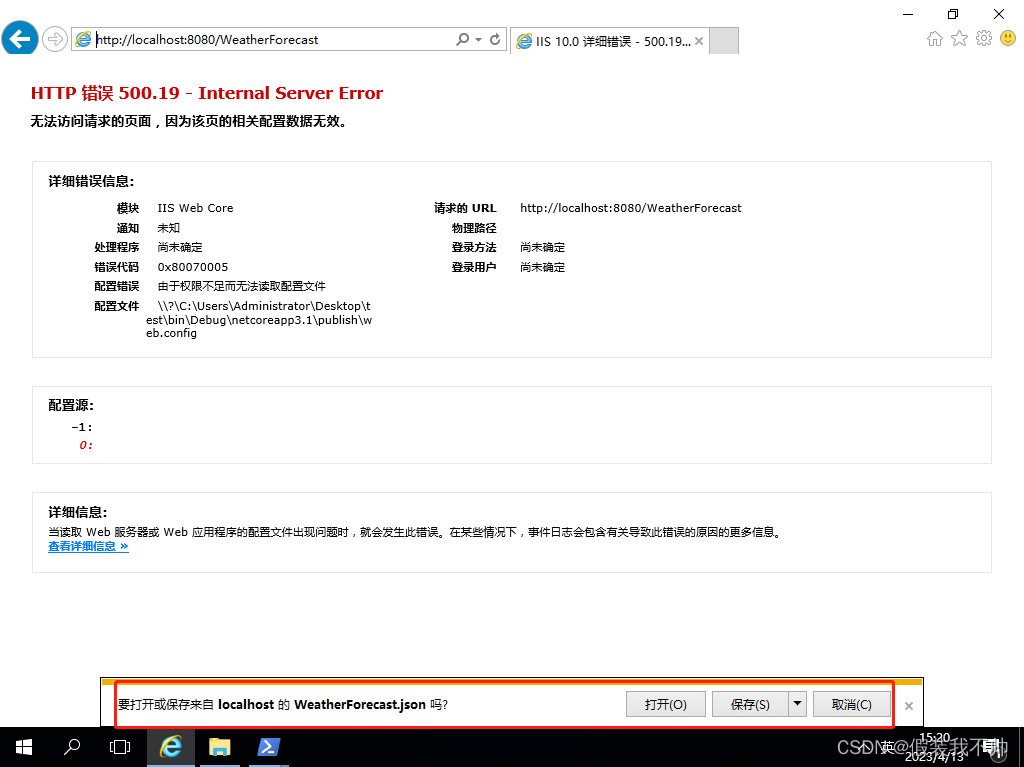
使用PowerShell自动部署ASP.NetCore程序到IIS
asp.net core 安装asp.net core sdk https://dotnet.microsoft.com/en-us/download/dotnet/3.1 创建asp.net core项目 dotnet new webapi运行项目 访问https://localhost:5001/WeatherForecast iis配置 安装iis 以管理员身份运行powershell Enable-WindowsOptiona…...
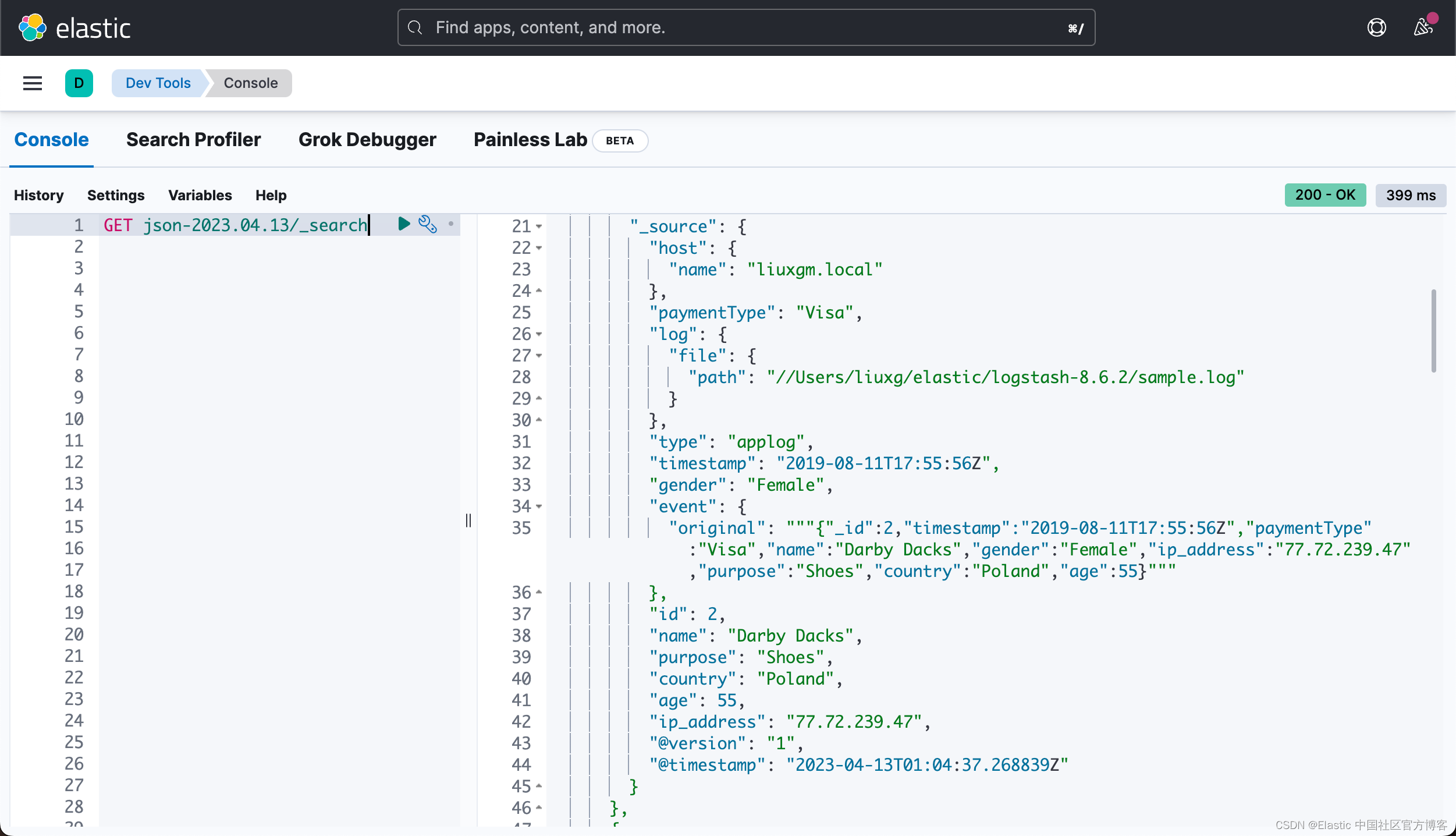
Elasticsearch:保留字段名称
作为 Elasticsearch 用户,我们从许多不同的位置收集数据。 我们使用 Logstash、Beats 和其他工具来抓取数据并将它们发送到 Elasticsearch。 有时,我们无法控制数据本身,我们需要管理数据的结构,甚至需要在摄取数据时处理字段名称…...
解密:迈向 Qt 网络编程之巅)
Qt 套接字类(QTcpSocket和QUdpSocket)解密:迈向 Qt 网络编程之巅
Qt 套接字类解密:迈向 Qt 网络编程之巅 一、套接字类简介(Introduction to Socket Classes)# 套接字类的作用(Role of Socket Classes)Qt 中常见套接字类概述(Overview of Common Socket Classes in Qt&…...

Python视频编辑库:MoviePy
MoviePy MoviePy是一个关于视频编辑的python库,主要包括:剪辑,嵌入拼接,标题插入,视频合成(又名非线性编辑),视频处理,和自定制效果。可以看gallery中的一些实例来了解用法。MoviePy可以读写所有的音频和视频格式,包括GIF,通过python2.7+和python3可以跨平台运行于window/M…...

课程3:ASP.NET Core 身份验证 - Cookie
课程简介目录 🚀前言一、.Net Core 身份验证简介二、开启Cookie身份验证三、添加登录接口3.1 添加登录Dto3.2 添加登录接口Login3.3 获取用户信息接口,添加身份验证四、获取用户信息接口测试4.1 测试获取用户信息接口4.2 登录4.3 再次测试:获取用户信息接口4.4 其他浏览器测…...

Visual Studio 2022如何安装和使用MSDN
我是荔园微风,作为一名在IT界整整25年的老兵,在后台收到提问,问我Visual Studio 2022如何安装和使用MSDN,这个我之前也没有在这个版本上装过MSDN,我之前是在Visual Studio 2017版上装过MSDN,那既然有人问了…...

82.qt qml-2D粒子系统、粒子方向、粒子项(一)
由于粒子系统相关的类比较多, 所以本章参考自QmlBook in chinese的粒子章节配合学习: 由于QmlBook in chinese翻译过来的文字有些比较难理解,所以本章在它的基础上做些个人理解,建议学习的小伙伴最好配合QmlBook in chinese一起学习。 1.介绍 粒子模拟的核心是粒子系统(Partic…...

引用的底层原理(汇编指令),引用与指针的联系与区别
TIPS 2. 3. 4. 引用的底层本质 在语法层面上的话,这个引用是不开空间的,相当于是对一个变量进行一个取别名的这么一个操作。在底层实现上实际是有空间的,因为引用是按照指针方式来实现的。然而如果你从底层的角度去看的话,因…...

磁盘的移臂调度算法
1、概要 访问磁盘,首先要找到数据,但机械硬盘并不是直接电子读取,是需要移动磁头到相应的数据块上才能读取的,即需要磁头移动到目标柱面(磁道),然后磁片旋转使磁头能访问到相应扇区,进而读取到数据。 根据访…...
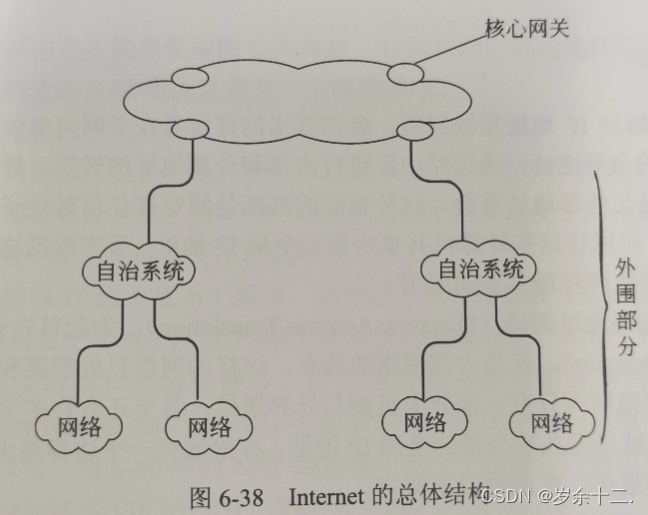
软考第六章 网络互连与互联网
网络互连与互联网 1.网络互连设备 组成因特网的各个网络叫做子网,用于连接子网的设备叫做中间系统。它的主要作用是协调各个网络的工作,使得跨网络的通信得以实现。 网络互连设备可以根据它们工作的协议层进行分类: 中继器:工…...

C6678-缓存和内存
C6678-缓存和内存 全局内存映射扩展内存控制器(XMC)-MPAX内存保护与地址扩展使用例程缓存 全局内存映射 扩展内存控制器(XMC)-MPAX内存保护与地址扩展 每个C66x核心都具有相同大小的L1和L2缓存,并且可配置为普通内存使…...

实操| 前端新人无敲代码开发APP
作为一种大型的基于GPT-3. 5结构的语言模型,ChatGPT由OpenAI训练,采用深度学习技术,通过大量的文本数据学习,可以生成类似于人类自然语言的文字。ChatGPT是一种非常强大的对话引擎,能进行对话、回答问题和完成任务。Ch…...

OpenCV图像处理之傅里叶变换
文章目录 OpenCV图像处理之傅里叶变换图像处理之傅里叶变换流程图OpenCv图像处理之傅里叶变换OpenCv傅里叶变换之低通滤波OpenCv傅里叶变换之高通滤波 OpenCV图像处理之傅里叶变换 傅里叶变换:目的就是得到图像的低频和高频,然后针对低频和高频进行不同…...

Docker网络案例
bridge 是什么 Docker 服务默认会创建一个 docker0 网桥(其上有一个 docker0 内部接口),该桥接网络的名称为docker0,它在内核层连通了其他的物理或虚拟网卡,这就将所有容器和本地主机都放到同一个物理网络。Docker 默认指定了 docker0 接口 的 IP 地址和子网掩码,让主机…...
Java实验课的学习笔记(二)类的简单使用
本文章就讲的是很基础的类的使用 重点大概就是类的构造函数以及一些很基础的东西。 实验内容是些老生常谈的东西,Complex类,在当初学C面向对象的时候也是这个样子展开的。 内容如以下: public class Complex {float real;float imag;public…...

实战案例|聚焦攻击面管理,腾讯安全威胁情报守护头部券商资产安全
金融“活水”润泽千行百业,对金融客户来说,由于业务场景存在特殊性和复杂性,网络安全必然是一场“持久战”。如何在事前做好安全部署,构建威胁情报分析的防护体系至为重要,实现更为精准、高效的动态防御。 客户名片 …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
