Python机器学习:支持向量机
这是我读本科的时候第一个接触到的机器学习算法,但也是第一个听完就忘的。。。
他的基本思想很简单:想办法把一个样本集划成两个部分:对于空间中的样本点集合,我们找到一个超平面把这个样本点集合给分成两个部分,其中一部分是正类,另一部分是反(负)类,支持向量机的优化目标就是找到一个超平面,使得空间中距离超平面最近的点到超平面的几何间距尽可能大,这些点就被称为支持向量。
首先得了解几个概念:
一、最大间隔和超平面:
和之前的一样,我们给定一个样本集合然后设定:
,设输入空间中的一个超平面为:
其中,是超平面的法向量,b为偏置,决定超平面的位置,根据点到直线的距离公式的扩展,空间中一点
到超平面
的欧氏距离为:
如果超平面可以把所有样本点分成两类,那实际上, 点到超平面
的欧氏距离就是一个分段函数:
好了,基本上把最大间隔和超平面给了解清楚了,说白了,就是,emm,我画个图来展示一下:
其实这个就是个很简单的东西,第四张可看可不看,主要是前三张图片,第一张是y1=sin(x)
第二张是y2=cos(x*pi/2),第三张是y3=y1+y2,那也就是说,怎么样才能从第三张图中把y1和y2给分离出来呢,学信号的同学这不就来精神了吗,那不就是,对吧,我直接一个傅里叶变换从时空域变到频率域,这不就很简单的能分开了嘛,so easy对吧,可是,这里,咱说的是支持向量机,也就是说,我们得用支持向量机的观点来给他把(x,y1)和(x,y2)这两个信号分开,怎么分开,我暂时就想了上面提到的变换到频率域去解决,当然,学信号的人会想到用滤波器或者其他方法,总之,有很多,但是具体怎么做呢,大家可以自己去试试,找找文献或者技术资料,来看看信号的分离或者是信号去噪这方面的,我只知道,方法很多。
二、线性可分支持向量机
QAQ,这个概念就要两页多,因为小学抄古诗抄怕了,我是真不喜欢抄书,,但是,抄吧,首先看一下他的目标是啥:通过求解和b,找到一个超平面,在保证这个超平面能偶正确将样本进行分类的同时,要使距离超平面最近的点到超平面的距离尽可能的大,说白了就是一个带约束条件的优化问题,其约束条件就是超平面可以把样本集合的点都给正确分类喽。
我们把距离超平面最近的点和超平面之间的距离记为
最优化问题就是:
我们可以对任一支持向量通过对超平面公式进行缩放,使得
然后到超平面的距离就是
,优化问题就能够写成
最大化,也就是最小化
,这里我用后者作为优化目标,就让你的计算可以方便了很多。
数学上是完全可以证明,支持向量机的超平面存在着唯一性,至少有两个支持向量,而且超平面的位置仅由这些支持向量决定。
再感知机的模型中,优化的目标很明确:
在满足模型能够正确分类的约束条件下,使得样本集合中所有点到分割超平面的距离最小,这样的超平面可能会有无数个。
然后,怎么求上面给出的最优化问题嘞?可以用拉格朗日乘子法来求解:
表示拉格朗日乘子,让lag函数对omega和b求偏导为零,然后计算就可以啦,详细的我就不写了,大家可以自己推一推,我也在纸上推一推,就不写latex了,嘿嘿。
相关文章:
Python机器学习:支持向量机
这是我读本科的时候第一个接触到的机器学习算法,但也是第一个听完就忘的。。。 他的基本思想很简单:想办法把一个样本集划成两个部分:对于空间中的样本点集合,我们找到一个超平面把这个样本点集合给分成两个部分,其中…...

矩阵和线性代数的应用
矩阵和线性代数是数学中重要的概念,它们被广泛应用于物理、工程、计算机科学、经济学等众多领域。本文将讨论矩阵和线性代数的一些基本概念以及它们在实际应用中的重要性和影响。 一、矩阵和线性代数的基本概念 矩阵是由数字组成的矩形数组。它可以表示线性方程组…...

六:内存回收
内存回收: 应用程序通过 malloc 函数申请内存的时候,实际上申请的是虚拟内存,此时并不会分配物理内存。 当应用程序读写了这块虚拟内存,CPU 就会去访问这个虚拟内存, 这时会发现这个虚拟内存没有映射到物理内存&…...

【cpolar 内网穿透】Openwrt 软路由实现内网穿透
cpolar 是一种安全的内网穿透云服务,它将内网下的本地服务器通过安全隧道暴露至公网。使得公网用户可以正常访问内网服务。 文章目录 前言一、上传 cpolar 安装包二、配置cpolar环境变量三、安装并配置 cpolar 服务3.1 安装 cpolar3.2 启动 cpolar3.3 进行其他配置 …...

Android 10.0 Camera2 拍照功能默认选前摄像头
1.概述 在10.0的系统产品开发中,对于app调用系统api来打开摄像头拍照的功能也是常有的功能,而拍照一般是默认打开后置摄像头拍照的,由于 客户的产品特殊要求,需要打开前置摄像头拍照功能,所以需要了解拍照功能的流程,然后修改默认前置摄像头打开拍照功能就可以了 app调…...
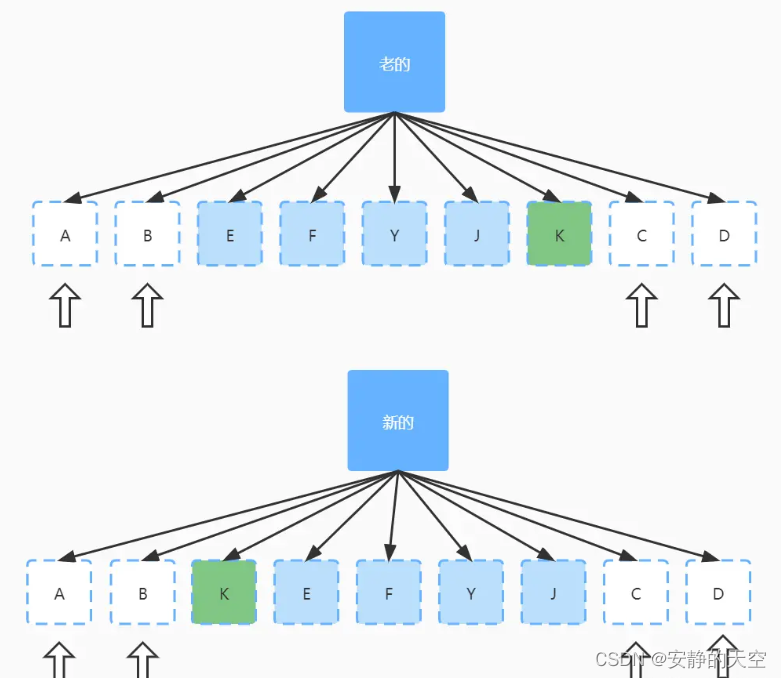
vue-vue2和vue3的diff算法
核心要点 数据变化时,vue如何更新节点虚拟DOM 和 真实DOM 的区别vue2 diff 算法vue3 diff 算法 一、 数据变化时,vue如何更新节点 首先渲染真实DOM的开销是很大,比如有时候我们修改了某个数据且修改的数据量很大时,此时会频繁的…...

一文解读基于PaddleSeg的钢筋长度超限监控方案
项目背景 钢铁厂生产钢筋的过程中会存在部分钢筋长度超限的问题,如果不进行处理,容易造成机械臂损伤。因此,需要通过质检流程,筛选出存在长度超限问题的钢筋批次,并进行预警。传统的处理方式是人工核查,该方…...
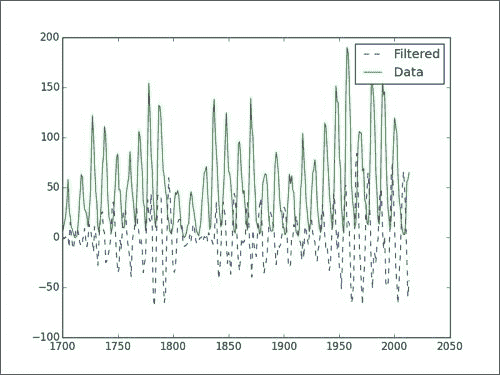
NumPy 数组学习手册:1~5
原文:Learning NumPy Array 协议:CC BY-NC-SA 4.0 译者:飞龙 一、NumPy 入门 让我们开始吧。 我们将在不同的操作系统上安装 NumPy 和相关软件,并查看一些使用 NumPy 的简单代码。 正如“序言”所述,SciPy 与 NumPy 密…...

【C++11】晦涩难懂语法系列:可变参数模板
目录 可变参数模板 1.1 概念 1.2 可变参数模板定义 1.3 参数包的展开方式 1.3.1 递归展开参数包 1.3.2 逗号表达式展开参数包 1.4 STL的emplace系列函数 可变参数模板 1.1 概念 在C语言阶段,我们已经接触过可变参数,比如scand、printf等等 这里…...
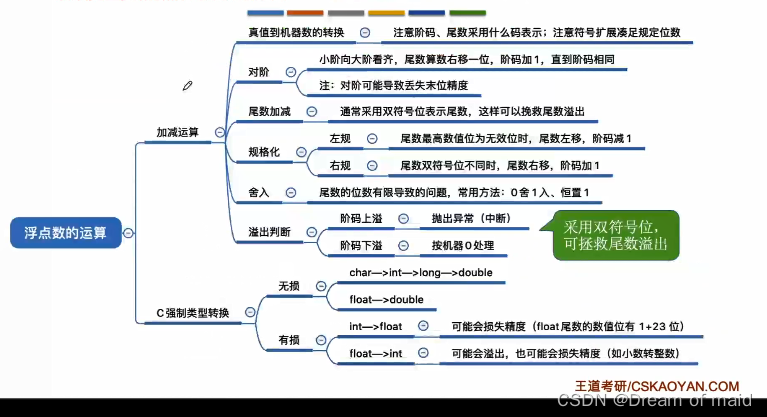
计算机组成原理第二章——数据的表示与运算(下)
提示:时光清浅处 一步一安然 文章目录 前言2.3.1 浮点数的表示2.3.2 IEEE7542.2.3 浮点数的运算 前言 本节主要讲三个问题,浮点数的表示,IEEE 754标准,浮点数的加减运算 2.3.1 浮点数的表示 浮点数的作用和基本原理 定点数可表…...
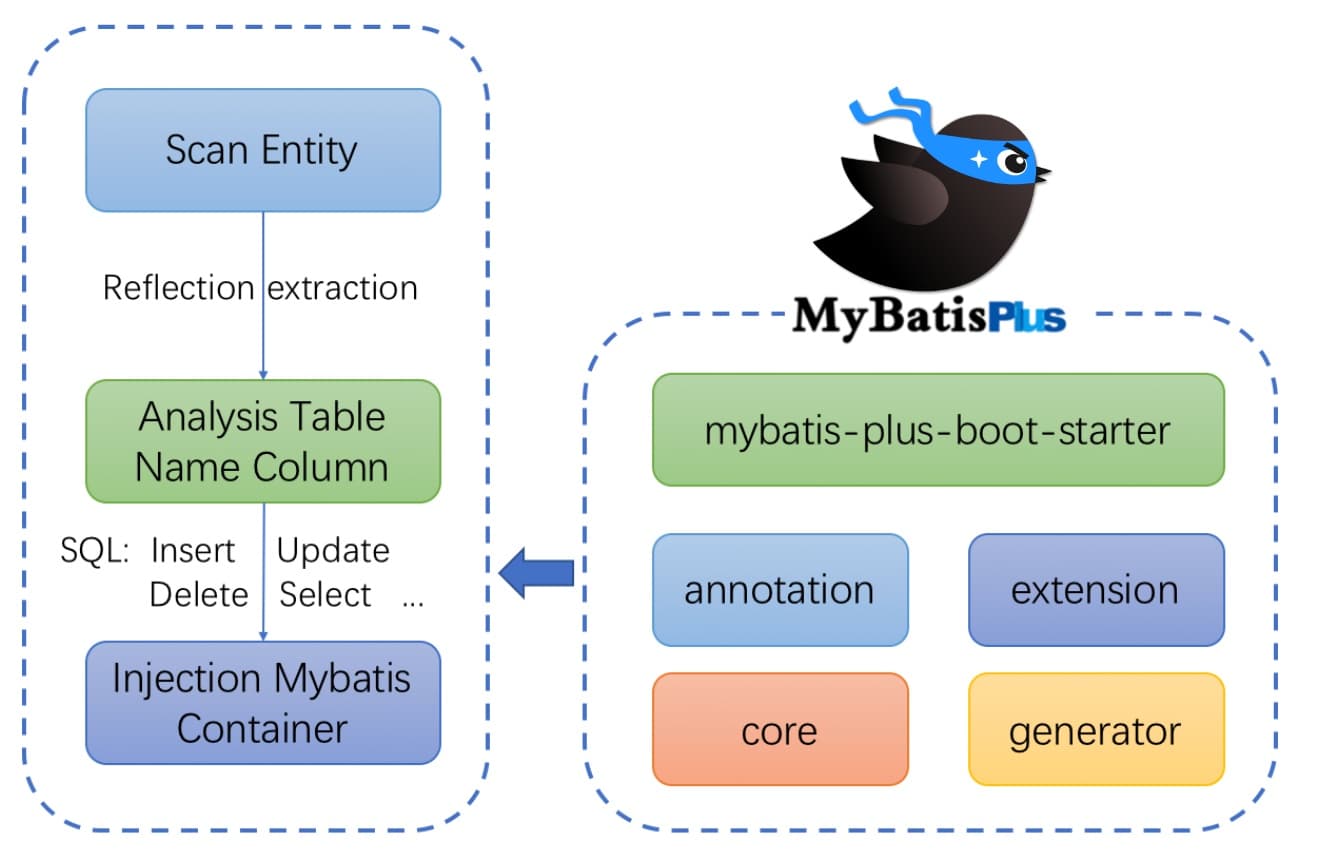
1.mybatis-plus入门及使用
1.什么是MybatisPlus MyBatis-Plus 官网 为什么要学MybatisPlus? MybatisPlus可以节省大量时间,所有的CRUD代码都可以自动化完成MyBatis-Plus是一个MyBatis的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效…...
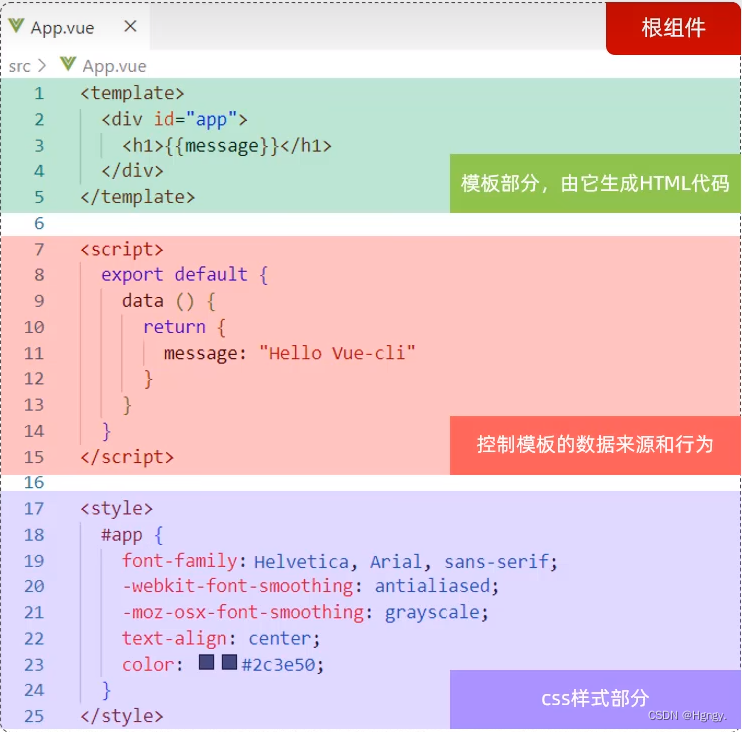
JavaWeb开发 —— 前端工程化
目录 一、前后端分离开发 二、YApi 三、前端工程化 1. 环境准备:vue-cli 2. Vue项目创建 四、Vue项目开发流程 一、前后端分离开发 ① 最早的前端开发就是实现页面,顶多再写写JS让页面可以有交互的特效。属于前后端未分离的时代。 早期前后端混合开…...

listener监听器框架
监听器是Web开发中常用的一种组件,用于监听某些事件并根据事件触发相应的处理逻辑。在Spring Boot中使用监听器可以方便地实现对程序中各种事件的监听,比如启动事件、关闭事件等。 首先需要定义一个监听器,通常需要实现ApplicationListener接…...
tp5实现导入excel表到数据库
hello,大家好,好长时间没有更新文章了。最近一直在忙着做项目。所以断更了。 那么好,各位老铁是否想要实现导入导出的功能 请关注我,解密如何实现导入导出, 那么今天先来讲一下用thinkphp5.0 如何实现Excel表格导入数据…...

Python基础-04 字符串
字符串的表示方式 在Python中,可以使用一对单引号/双引号或者一对三个双引号/一对三个单引号表示字符串 a hello b "hello" c hello d """hello""" # 如果字符串里面还有双引号,外面就可以使用单引号 # 反之一样 # 如果字符串里…...

VVC之编码结构
VVC之编码结构(新一代通用视频编码的读书笔记) 缩写概述EncAppmain函数解读 缩写 缩写含义CVSCoded Video Sequence, 编码视频序列IRAPIntra Random Access Point, 帧内随机接入点GDRGradual Decoding Refresh, 逐渐解码刷新AUAccess Unit, 访问单元PUP…...

FPGA基于SFP光口实现10G万兆网UDP通信 10G Ethernet Subsystem替代网络PHY芯片 提供工程源码和技术支持
目录 1、前言2、我这里已有的UDP方案3、详细设计方案4、vivado工程详解5、上板调试验证并演示6、福利:工程代码的获取 1、前言 目前网上的fpga实现udp基本生态如下: 1:verilog编写的udp收发器,但不带ping功能,这样的代…...
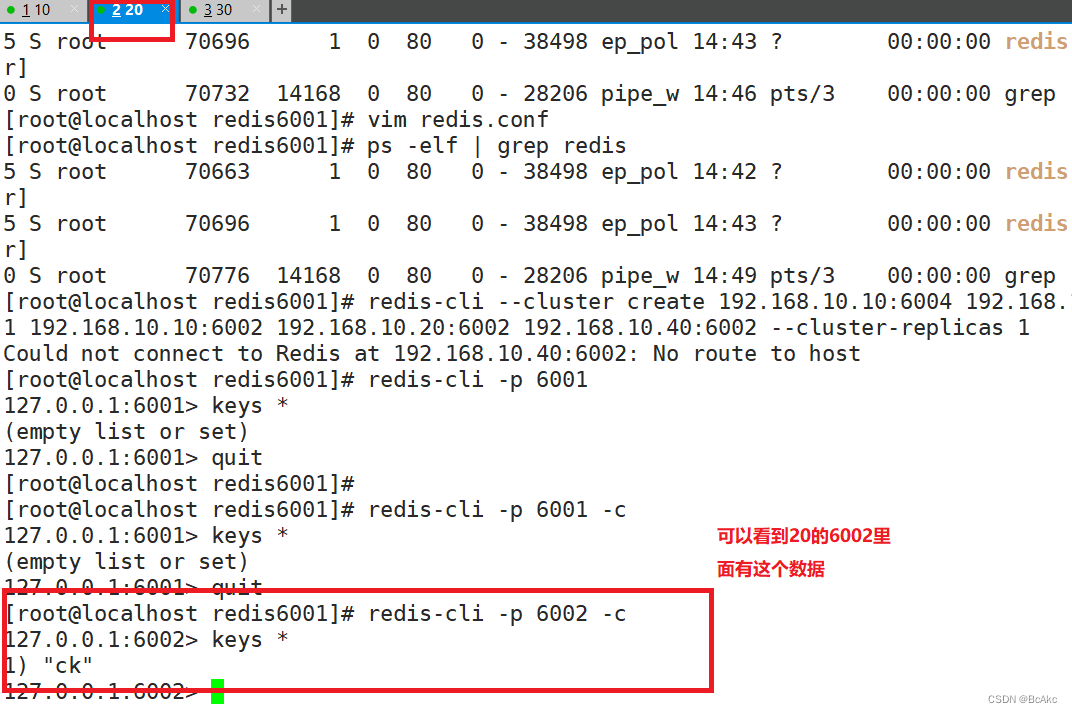
Linux Redis主从复制 | 哨兵监控模式 | 集群搭建 | 超详细
Linux Redis主从复制 | 哨兵监控模式 | 集群搭建 | 超详细 一 Redis的主从复制二 主从复制的作用三 主从复制的流程四 主从复制实验4.1 环境部署4.2 安装Redis(主从服务器)4.3 修改Master节点Redis配置文件 (192.168.163.100)4.4 修改Slave节点Redis配置…...

整柜海运到美国的规格和收费标准是什么
整柜海运是指将所有货物安装在一个整箱内,由发货人和收货人共同操作,而目的港的收货人一般只有一个,方便操作。整柜海运到美国的主要流程有以下几个步骤:订舱、装柜、报关、海运、清关、提柜和送货。实际上,国际物流出…...
Session和Cookie区别介绍+面试题
Session 会话: 对应的英文单词:session用户打开浏览器,进行一系列操作,然后关闭浏览器。整个过程叫做一次会话一个会话包含多次请求 session机制属于B/S结构的一部分,主要的作用就是为了保存会话状态。(用户登录成功后…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
