计算机组成原理第二章——数据的表示与运算(下)
提示:时光清浅处 一步一安然
文章目录
- 前言
- 2.3.1 浮点数的表示
- 2.3.2 IEEE754
- 2.2.3 浮点数的运算
前言
本节主要讲三个问题,浮点数的表示,IEEE 754标准,浮点数的加减运算
2.3.1 浮点数的表示
浮点数的作用和基本原理
定点数可表示的数字范围有限,但我们不能无限制地增加数据的长度
将一个数值用阶码和尾数来表示,这样表示的数值的范围就大大增加了,

浮点数规格化
尾数的最高位是无效位会丧失精度,规定尾数的最高数值位必须是一个有效值
左规:当浮点数运算的结果为非规格化时要进行规格化处理,讲尾数算数左移一位,阶码减一
右规:当浮点数运算的结果尾数出现溢出,(双符号位为01或10,双符号位中的更高位表示我们当前数值的正负性)时,将尾数算数右移一位,新空出的位置与与双符号位保持一致,这里也就是零,最后阶码加一
采用双符号位,当溢出发生时候,可以挽救,更高的符号位是正确的符号位

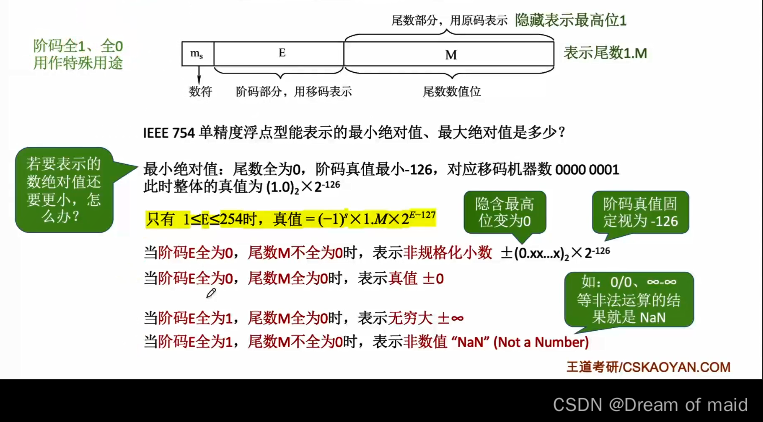
浮点数的表示范围
这里要注意用补码表示的负数的尾数,我们为了计算机处理起来方便,我们规定数值位的最高位必须是0,正数依然是1,也就是当符号位为0的时候 数值位为1 当符号位为1的时候数值位为0,如下图右下的例题,我们知道负数的补码是补1的,并且规格化是需最高位为0的,所以也就需要算数左移三位,此时阶码值就要减3

知识点回顾
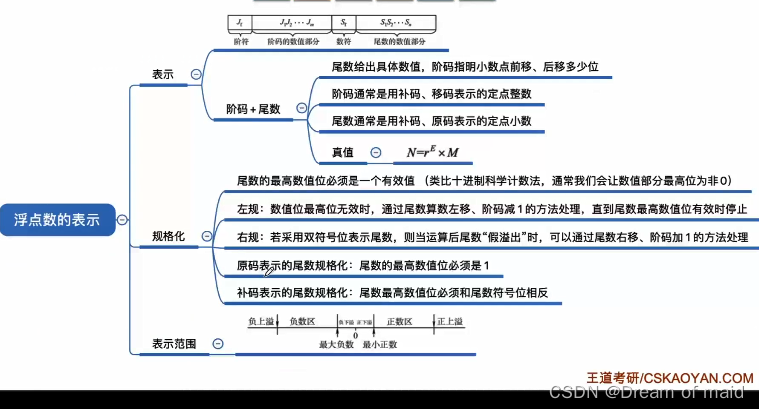
2.3.2 IEEE754
移码
我们上面说过阶码可以使用移码或者补码来,尾数也可以使用原码或者补码来表示,所以也就需要某些标准,
补码的基础上将符号位取反就能得到移码,注意移码只能用于表示整数
移码的定义:移码=真值+偏置值,此处8位移码的偏置值=128d=1000 0000B 偏置值一般取128D 此时移码=补码符号位取反,IEEEE754取的偏置值127时,此时对于真值-128=1000 0000B 移码=-1000 0000 +0111 1111=1111 1111(这里的计算时是发现被减数比减数要小,由于我们移码只有8bit,所以背后的这些加减运算都会进行mod128,我们可以在原有的基础上加上128,然后再减 此时得到的移码便是1111 1111)
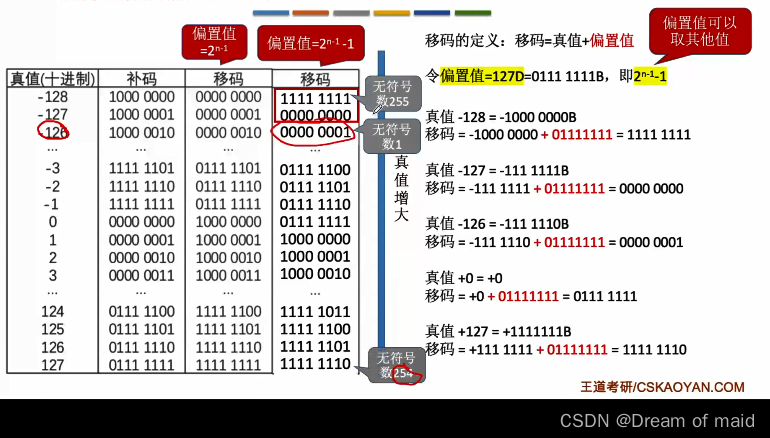
IEEE754
这个表格需要记住,并且在计算时,可以将这个移码看成一个无符号数,然后用之前的计算方式 比如下图double中的蓝色部分的,可以看成无符号数128(移码)-1023(偏移量)
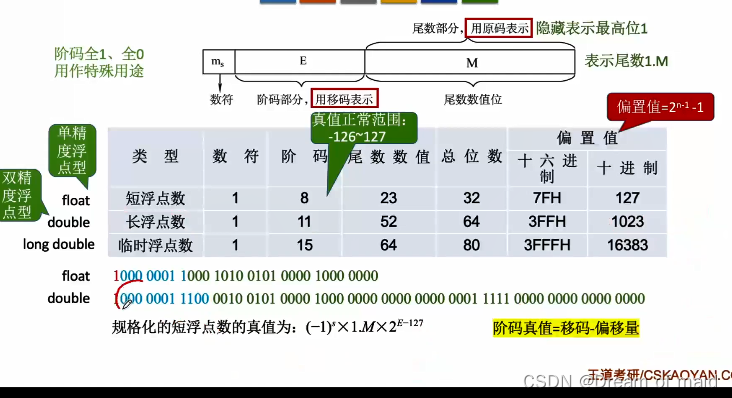


数值范围
之前我们说过-128(全1) -127(全0)有其他用处 所以这里阶码的最小值时-126,所以范围如下
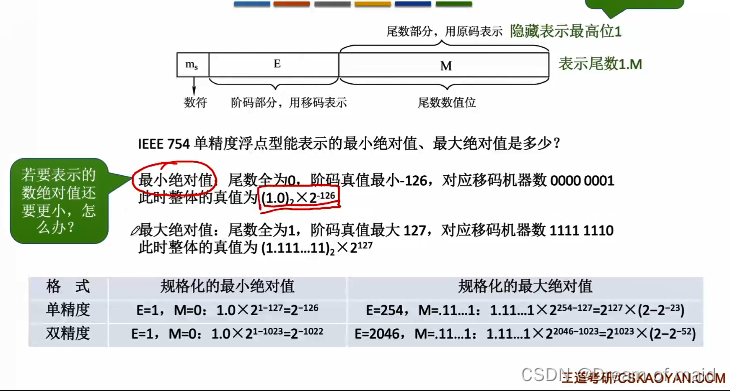
虽然在偏置值为127 时,移码全0 事实上的对应的-127次方,但是这里下图我们会把它固定的视为-126次方,此时是正无穷还是负无穷是看其中的数符位
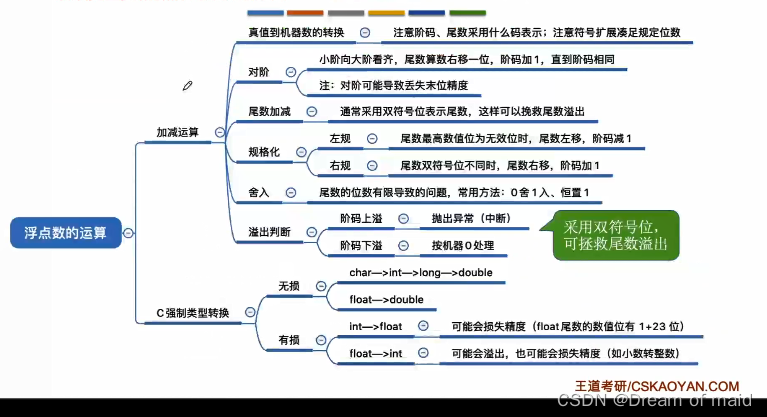
2.2.3 浮点数的运算
本节主要讲的是浮点数的加减法运算,以及强制类型转换
小阶向大阶靠齐是为了计算机内部硬件的实现方便

它的两个符号位是否相同 相同则没有越界,如这里的11 就没有越界
舍入问题
除了右规的时候会面临舍入的问题,有的计算机可能会浮点数的尾数部分单独拆出来计算24bit->32bit 算完结果在经过舍入32bit->24bit再拼回浮点数

本节回顾
相关文章:

计算机组成原理第二章——数据的表示与运算(下)
提示:时光清浅处 一步一安然 文章目录 前言2.3.1 浮点数的表示2.3.2 IEEE7542.2.3 浮点数的运算 前言 本节主要讲三个问题,浮点数的表示,IEEE 754标准,浮点数的加减运算 2.3.1 浮点数的表示 浮点数的作用和基本原理 定点数可表…...
1.mybatis-plus入门及使用
1.什么是MybatisPlus MyBatis-Plus 官网 为什么要学MybatisPlus? MybatisPlus可以节省大量时间,所有的CRUD代码都可以自动化完成MyBatis-Plus是一个MyBatis的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效…...
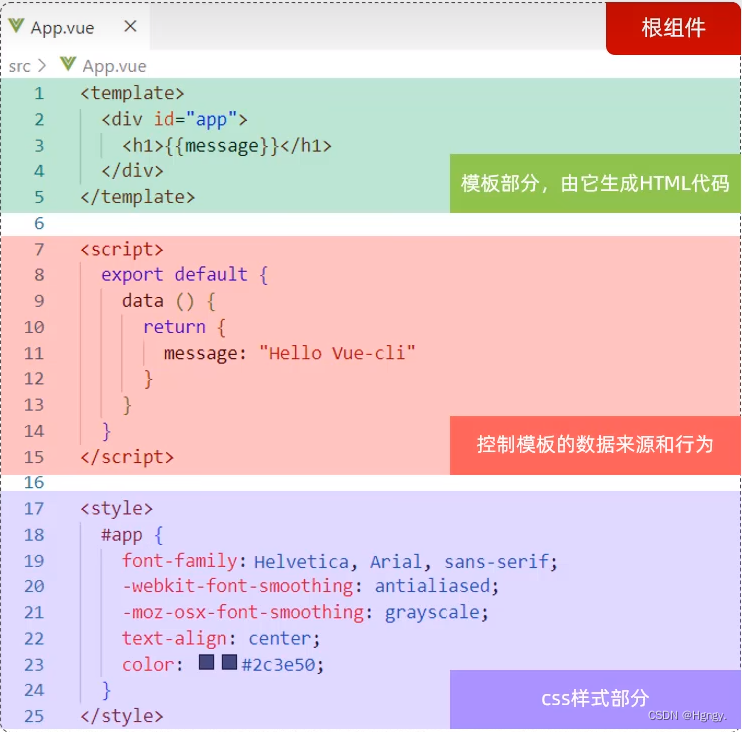
JavaWeb开发 —— 前端工程化
目录 一、前后端分离开发 二、YApi 三、前端工程化 1. 环境准备:vue-cli 2. Vue项目创建 四、Vue项目开发流程 一、前后端分离开发 ① 最早的前端开发就是实现页面,顶多再写写JS让页面可以有交互的特效。属于前后端未分离的时代。 早期前后端混合开…...

listener监听器框架
监听器是Web开发中常用的一种组件,用于监听某些事件并根据事件触发相应的处理逻辑。在Spring Boot中使用监听器可以方便地实现对程序中各种事件的监听,比如启动事件、关闭事件等。 首先需要定义一个监听器,通常需要实现ApplicationListener接…...
tp5实现导入excel表到数据库
hello,大家好,好长时间没有更新文章了。最近一直在忙着做项目。所以断更了。 那么好,各位老铁是否想要实现导入导出的功能 请关注我,解密如何实现导入导出, 那么今天先来讲一下用thinkphp5.0 如何实现Excel表格导入数据…...

Python基础-04 字符串
字符串的表示方式 在Python中,可以使用一对单引号/双引号或者一对三个双引号/一对三个单引号表示字符串 a hello b "hello" c hello d """hello""" # 如果字符串里面还有双引号,外面就可以使用单引号 # 反之一样 # 如果字符串里…...

VVC之编码结构
VVC之编码结构(新一代通用视频编码的读书笔记) 缩写概述EncAppmain函数解读 缩写 缩写含义CVSCoded Video Sequence, 编码视频序列IRAPIntra Random Access Point, 帧内随机接入点GDRGradual Decoding Refresh, 逐渐解码刷新AUAccess Unit, 访问单元PUP…...

FPGA基于SFP光口实现10G万兆网UDP通信 10G Ethernet Subsystem替代网络PHY芯片 提供工程源码和技术支持
目录 1、前言2、我这里已有的UDP方案3、详细设计方案4、vivado工程详解5、上板调试验证并演示6、福利:工程代码的获取 1、前言 目前网上的fpga实现udp基本生态如下: 1:verilog编写的udp收发器,但不带ping功能,这样的代…...
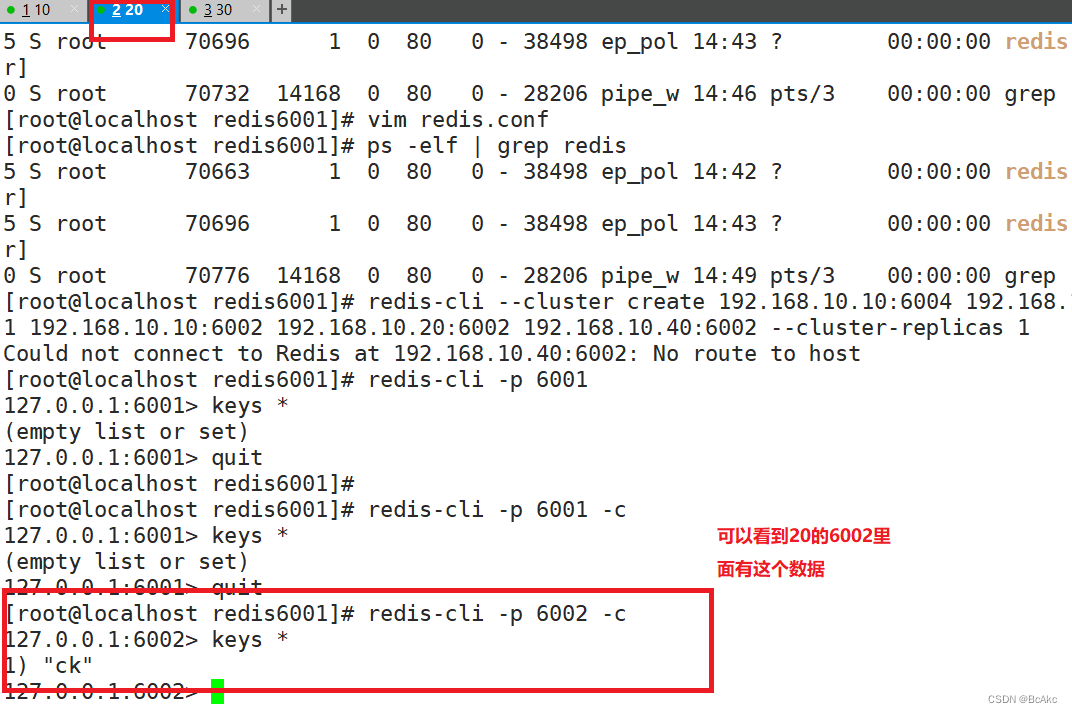
Linux Redis主从复制 | 哨兵监控模式 | 集群搭建 | 超详细
Linux Redis主从复制 | 哨兵监控模式 | 集群搭建 | 超详细 一 Redis的主从复制二 主从复制的作用三 主从复制的流程四 主从复制实验4.1 环境部署4.2 安装Redis(主从服务器)4.3 修改Master节点Redis配置文件 (192.168.163.100)4.4 修改Slave节点Redis配置…...

整柜海运到美国的规格和收费标准是什么
整柜海运是指将所有货物安装在一个整箱内,由发货人和收货人共同操作,而目的港的收货人一般只有一个,方便操作。整柜海运到美国的主要流程有以下几个步骤:订舱、装柜、报关、海运、清关、提柜和送货。实际上,国际物流出…...
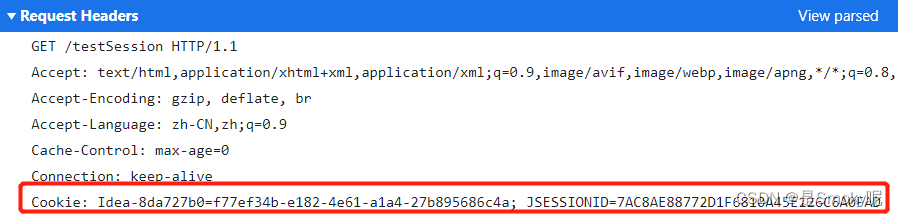
Session和Cookie区别介绍+面试题
Session 会话: 对应的英文单词:session用户打开浏览器,进行一系列操作,然后关闭浏览器。整个过程叫做一次会话一个会话包含多次请求 session机制属于B/S结构的一部分,主要的作用就是为了保存会话状态。(用户登录成功后…...
easyx
普通的画线图什么的 首先我们需要安装一个easyx的图形库,然后把头文件搞出来 #include <stdio.h> #include <easyx.h>//easyx画线啥啥的图形库 #include <graphics.h> #include <math.h> #include <conio.h>//键盘操作的头文件 设…...

记一次科学
华为云与Centos8 华为云99元Hongkong的服务器:1M,1C,2G,40G,自带不可更改的Centos 8.2 64bit 华为yum源不可以,网上找了可用的CentOS8 官方源不支持后配置yum源 # 备份 mv /etc/yum.repos.d/CentOS-Base…...

亚马逊被人差评了怎么办?
第一种: 也是最简单的做法就是通过电话或者邮件联系留差评的买家,大致意思就是按照货值的2-3倍作为赔偿,能不能把差评给删了 赔偿一个普通产品2-3倍的价格比起找服务商删一个差评几百到一千不等可以说是绰绰有余了,碰到那种愿意…...

【目标检测】YOLOv5:修改自己的网络结构
前言 YOLOv5就像一座金矿,里面有无数可以学习的东西。之前的博文一直将YOLOv5当作一个黑盒使用,只考虑模型的输入和输出,以此来对模型进行二次开发。 本篇博文将更近一层,深入到“金矿”内部,来尝试对模型结构进行替换…...

spring boot 工程整合mongodb,遇到的坑
首先说一下背景,因为其他的一个web工程有使用mongo,我想着给另外一个工程把mongo也加过来吧。也是最近做一个发送 丘比特信 的需求,觉得这个信应该是存到 mongodb。结果拿过来遇到了很大的坑,也是对版本对原理不了解吧。 下面介…...
)
防抖函数(最全 最干净 最好理解)
1.应用场景 1.input输入框 输入远程查询 2.邮箱,手机号验证,用户名验证 3.resize等高评率场景 2.解决问题 高频场景带来的重复渲染 等问题 多次操作 只在操作结束后再执行操作函数 3.具体实现 3.1this问题(因为settimeout是window的对…...
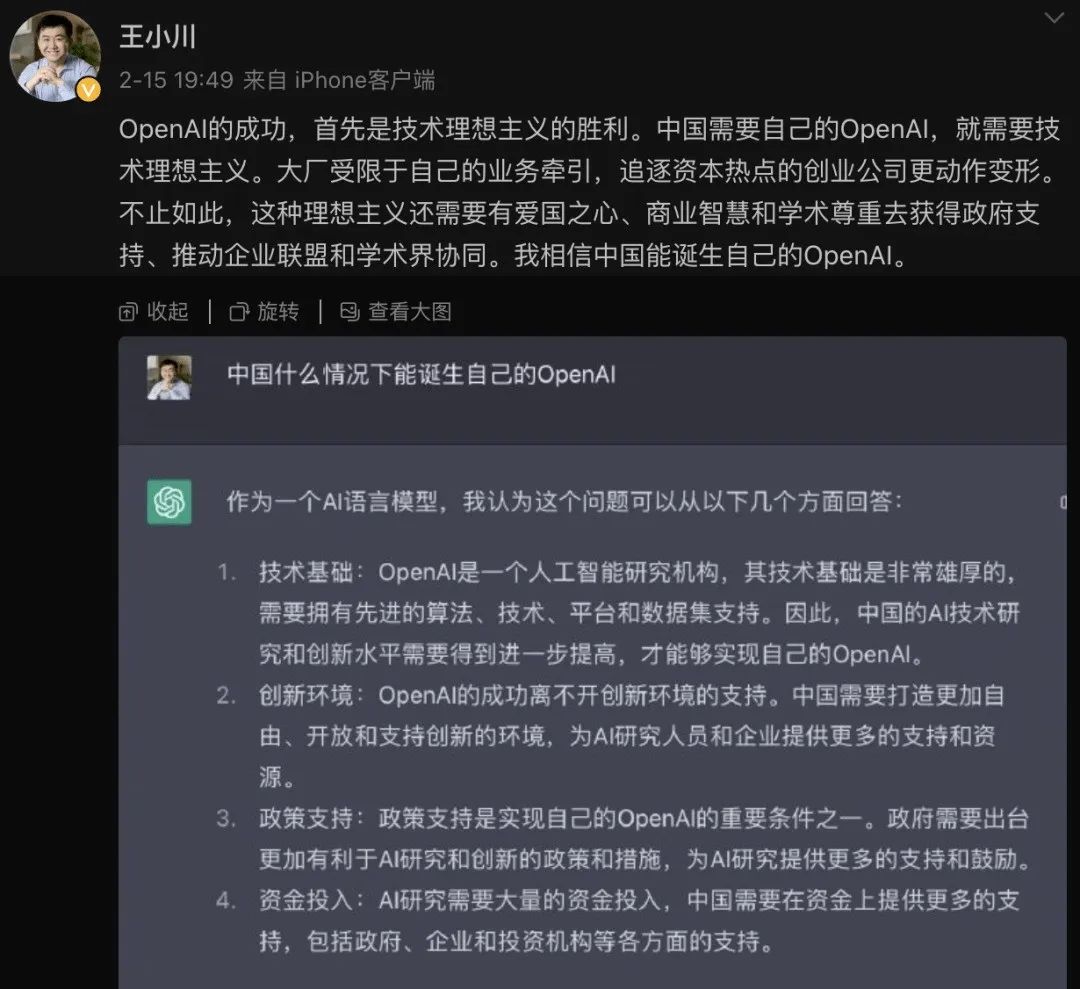
王小川,才是深「爱」李彦宏的那个人?
在推出中国首个类ChatGPT产品「文心一言」后,李彦宏在接受专访时断言,中国基本不会再出一个OpenAI了,「创业公司重新做一个ChatGPT其实没有多大意义,基于大语言模型开发应用机会很大,没有必要再重新发明一遍轮子。」 听…...

南京邮电大学通达学院2023《电子装配实习》报告
南京邮电大学通达学院2023《电子装配实习》报告 一 声明二 题目/实习报告提示三 例答 红笺寄 休遣玉人知 ——赠nmy 一 声明 南京邮电大学通达学院2023《电子装配实习》报告 答案更新时间:2023.04.10,已更新完成,如无错误不在更新 由于作者解答能力有限…...
Linux--tty
Linux 终端(TTY) TTY 是 Teletype 或 Teletypewriter 的缩写,原来是指电传打字机,后来这种设备逐渐键盘和显示器取代。不管是电传打字机还是键盘显示器,都是作为计算机的终端设备存在的,所以 TTY 也泛指计算机的终端(terminal)设…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...

ubuntu清理垃圾
windows和ubuntu 双系统,ubuntu 150GB,开发用,基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小,发现 .cache 有26GB,.local 有几个GB&am…...

边缘计算设备全解析:边缘盒子在各大行业的落地应用场景
随着工业物联网、AI、5G的发展,数据量呈爆炸式增长。但你有没有想过,我们生成的数据,真的都要发回云端处理吗?其实不一定。特别是在一些对响应时间、网络带宽、数据隐私要求高的行业里,边缘计算开始“火”了起来&#…...

第6章:Neo4j数据导入与导出
在实际应用中,数据的导入与导出是使用Neo4j的重要环节。无论是初始数据加载、系统迁移还是数据备份,都需要高效可靠的数据传输机制。本章将详细介绍Neo4j中的各种数据导入与导出方法,帮助读者掌握不同场景下的最佳实践。 6.1 数据导入策略 …...
