【C++】二叉树之力扣经典题目1——详解二叉树的递归遍历,二叉树的层次遍历
如有错误,欢迎指正。
如有不理解的地方,可以私信问我。
文章目录
- 题目1:根据二叉树创建字符串
- 题目
- 实例
- 思路与解析
- 代码实现
- 题目2:二叉树的层序遍历
- 题目
- 思路与解析
- 代码实现
题目1:根据二叉树创建字符串
点击进入题目链接——>力扣–根据二叉树创建字符串
题目
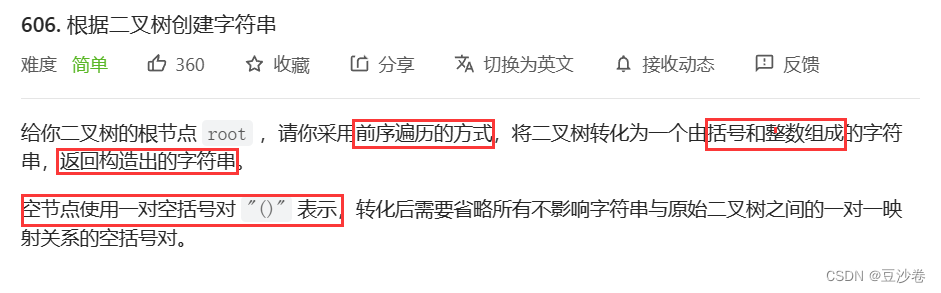
实例
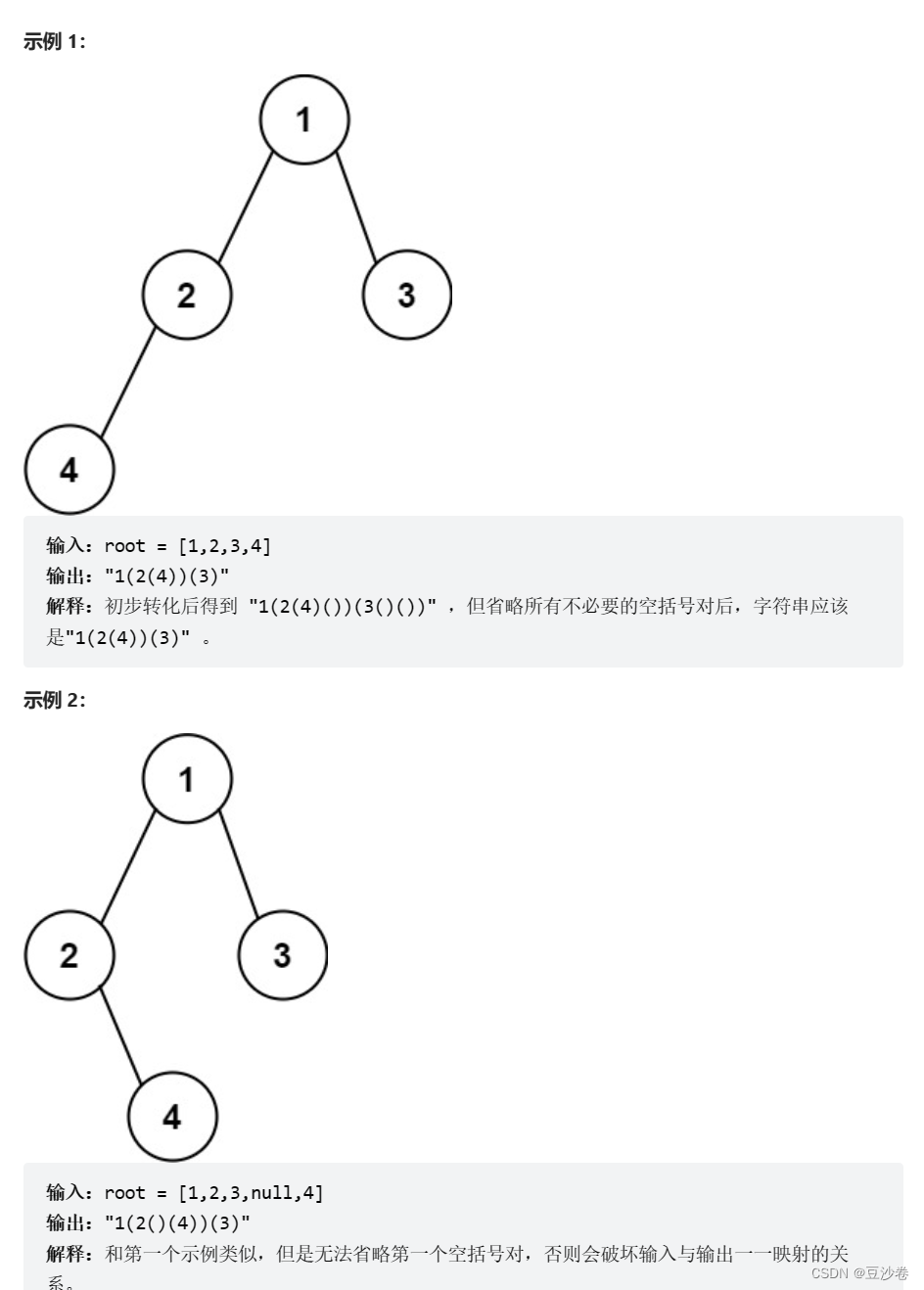
思路与解析
题目的要求:二叉树已给出,我们需要采用前序遍历的方式,遍历二叉树,空节点用()表示
即用()标识左右子树,但是结果需要省略不必要的空括号对,并把遍历的结果放在字符串中,最后返回的是字符串。
思路解析:这道题是二叉树层序遍历的变形,前序遍历—根,左子树,右子树—采用递归,我们主要解决的是空括号对的省略问题,明确什么时候需要省略。
步骤:
- 如果是空树就直接返回空字符串
- 创建存放前序遍历结果的字符串要将整数转换成字符串,才能插入到字符串对象中
- 我们可以使用递归的方法得到二叉树的前序遍历,并在递归时加上额外的括号。用()标识左右子树,但是需要省略所有不必要的空括号对
- 如果当前节点有两个孩子,那我们在递归时,需要在两个孩子的结果外都加上一层括号;
- 如果当前节点没有孩子,那我们不需要在节点后面加上任何括号;
- 如果当前节点只有左孩子,那我们在递归时,只需要在左孩子的结果外加上一层括号,而不需要给右孩子加上任何括号;
- 如果当前节点只有右孩子,没有左孩子,那我们在递归时,需要先加上一层空的括号 ‘()’,‘()’ 表示左孩子为空,再对右孩子进行递归,并在结果外加上一层括号。
- 最后返回存放层序遍历结果的字符串
代码实现
//思路:前序遍历---根,左子树,右子树---采用递归
class Solution {
public:string tree2str(TreeNode* root) {//1.如果是空树就返回空字符串if(root==nullptr){return string();}string str;//存放前序遍历结果的字符串//【根】str+=to_string(root->val);//要将整数转换成字符串//用()标识左右子树,但是需要省略所有不必要的开括号对//【左子树】//2.左子树不为空,所以我们需要标示左子树if(root->left){str+="(";//字符串+=用""或者‘’都可以str+=tree2str(root->left);str+=')';}else if(root->right)//3.如果左子树为空,右子树不为空,根据示例2,左子树为空,()不能省略,我们就手动加上{str+="()";}//【右子树】//4.对右子树的处理,我们需要标识右子树,从示例1中得,右子树为空,不需要加上()if(root->right){str+='(';str+=tree2str(root->right);str+=')';}return str;}
};
题目2:二叉树的层序遍历
点击进入题目链接——>力扣—二叉树的层序遍历
题目

思路与解析
思路:这道题考查二叉树的层序遍历,是层序遍历的变形,与普通的层序遍历不同的是,这道题的函数要求我们返回一个二维数组,所以我们需要先创建一个二维数组,二维数组中的一维数组分别存放二叉树每层的数据,根据题目的实例,我们要一层一层的遍历,将每层的遍历分别放在一维数组中,并利用队列的帮助进行层序遍历。接下来我们利用一个变量levelSize,这样可以准确的分开每层的数据,分别放在一维数组中。
代码实现
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> vv;//构建二维数组queue<TreeNode*> q;//存放二叉树结点的队列int levelSize=0;//每层的的结点个数if(root){q.push(root);levelSize=1;}while(!empty(q)){//构建一维数组,分别存放每层遍历的结果,一次循环结束后就push进二维数组vector<int> v;//levelSiz记录当前层的数据个数while(levelSize--)//关键思路:保证层序遍历{TreeNode* front=q.front();//保留队头结点地址q.pop();//出队头结点v.push_back(front->val);//将每层拿到的数据放进一维数组//push左子树if(front->left){q.push(front->left);}//push右子树if(front->right){q.push(front->right);}}levelSize=q.size();//将levelSize更改成当前成的数据个数vv.push_back(v);//将一维数组v(分别存放这每层的数据)push进二维数组vv中}return vv;}
};
变化:给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)点击进入题目:二叉树层序遍历II
解决方法:得到从上自下的层序遍历的二维数组后,用reverse函数,将二维数组中的内容翻转一下即可。
相关文章:

【C++】二叉树之力扣经典题目1——详解二叉树的递归遍历,二叉树的层次遍历
如有错误,欢迎指正。 如有不理解的地方,可以私信问我。 文章目录题目1:根据二叉树创建字符串题目实例思路与解析代码实现题目2:二叉树的层序遍历题目思路与解析代码实现题目1:根据二叉树创建字符串 点击进入题目链接—…...
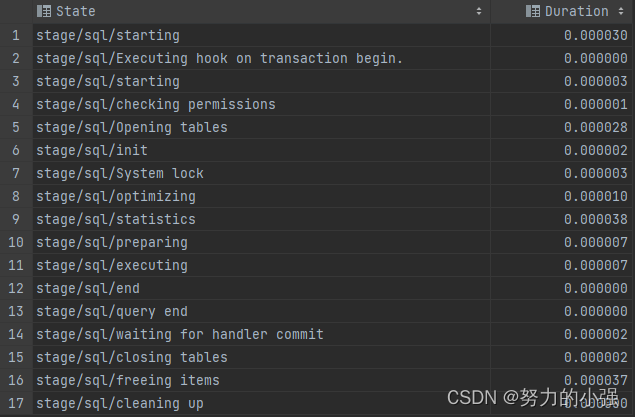
MySQL数据库调优————SQL性能分析
TIPS 本文基于MySQL 8.0 本文探讨如何深入SQL内部,去分析其性能,包括了三种方式: SHOW PROFILEINFORMATION_SCHEMA.PROFILINGPERFORMANCE_SCHEMA SHOW PROFILE SHOW PROFILE是MySQL的一个性能分析命令,可以跟踪SQL各种资源消耗。…...
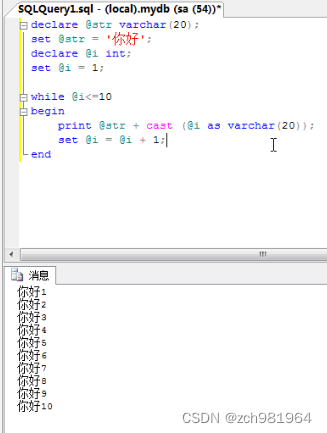
sql数据库高级编程总结(一)
1、数学函数:操作一个数据,返回一个结果 (1)取上限 ceiling 如果有一个小数就取大于它的一个最小整数 列如9.5 就会取到 10 select code,name,ceiling(price) from car (2)取下限 floor 如果有一个小数就…...

软件工程(5)--喷泉模型
前言 这是基于我所学习的软件工程课程总结的第五篇文章。 迭代是软件开发过程中普遍存在的一种内在属性。经验表明,软件过程各个阶段之间的迭代或一个阶段内各个工作步骤之间的迭代,在面向对象范型中比在结构化范型中更常见。 一般说来,使用…...

SM2数字签名
文章目录6. 签名流程7. 验签流程实现参考资料6. 签名流程 M’ ZA || Msge Hash(M’),并转为大数;生成随机数k,范围0<k<n;计算kG (x1, y1)r (e x1) mod n, 若r0或(rkn)则重新生成k;s (k-rd) / (1d) mod n&…...

RPA+保险后台部门擦出不一样“火花” | RPA案例
在保险行业中,后台业务线主要是为前台和中台等提供支持,提供公司整体运营服务,包括财务、信息、人力、综合办等。相对于中前台部门,后台部门离核心价值链更远一些,更偏支持部门,其中某些岗位与业务相关度强…...

设备树相关概念的理解
设备树 定义 设备树是描述硬件信息的一种树形结构,设备树文件会在内核启动后被内核解析得到对应设备的具体信息。 树形结构就自然会存在节点,硬件设备信息就存储再设备树中的节点上,即设备节点。而一个设备节点中可以存储硬件的多个不同属性…...

ubuntu20.04下配置深度学习环境GPU
卸载子系统 C:\Users\thzn>wsl --list 适用于 Linux 的 Windows 子系统分发版: docker-desktop (默认) docker-desktop-data Ubuntu-18.04 Ubuntu-22.04 Ubuntu-20.04 C:\Users\thzn>wsl --unregister Ubuntu-18.04 ubuntu 换源 https://www.cnblogs.com/Horizon-asd/p…...
)
用egg.js来写一个api管理系统(一)
Egg.js是一个基于Node.js的企业级开发框架,非常适合构建API服务。 安装egg.js 首先,您需要安装Node.js和npm(Node Package Manager)。然后,您可以通过运行以下命令来安装Egg.js: npm i egg --save然后&a…...
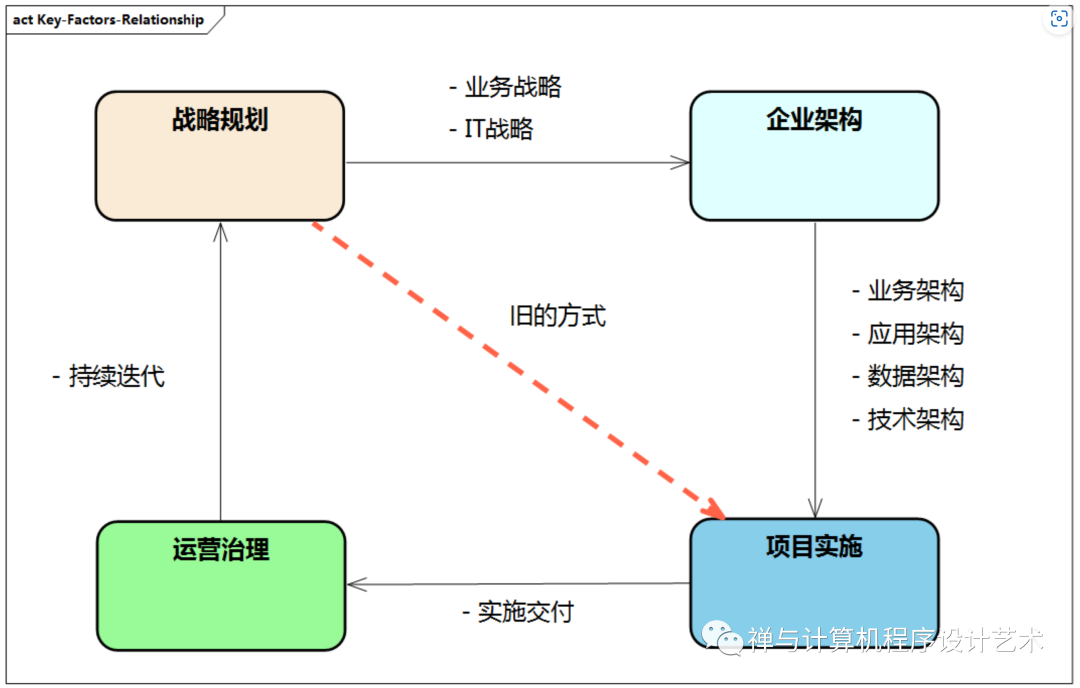
企业数字化转型和升级:架构设计方法与实践
目录 企业架构整体结构 企业架构的驱动力 企业架构的基本概念 企业架构的发展 企业架构框架理论 主流企业架构框架之对比 企业架构整体结构 图例:企业架构整体结构 企业架构整体结构从战略层、规划层、落地层这三层来分别对应企业架构中 业务、架构和实施的各种重要…...

【LeetCode】环形链表 II [M](链表)
142. 环形链表 II - 力扣(LeetCode) 一、题目 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链…...
系统)
Unity之如何实现一个VR任务(剧情)系统
一.前言 最近再做一个VR项目,里面有大量的剧情和VR操作任务。 比如: 1.张三说了什么话,干了什么事,然后,李四又说了什么,做了什么动画,完了之后,场景中某个物体高亮,让我们触摸或者射线点击(pc的话鼠标点击)和其发生交互。 2.我们使用VR手柄或者鼠标与场景中的一个…...
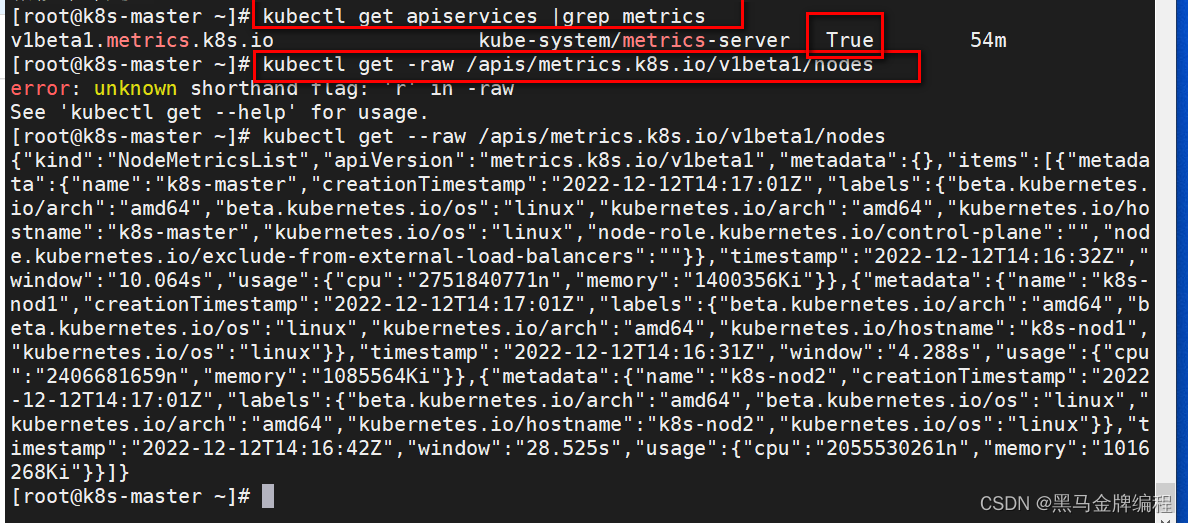
k8s核心概念与kubectl命令行工具的使用
k8s官方文档Kubernetes 文档 | Kubernetes作用:kubernetes用于容器化应用程序的部署,扩展和管理。目标:是让部署容器化应用简单高效。Kubernetes集群架构与组件 Master组件 kube-apiserverkubernetes API,集群的统一入口ÿ…...

【零基础入门前端系列】—无序列表、有序列表、定义列表(四)
一、HTML无序列表 无序列表是一个项目的列表,此列项目使用粗体圆点(典型的小黑圆圈)进行标记。 无序列表使用 <ul> 标签 <ul> <li>Coffee</li> <li>Milk</li> </ul>嵌套结构: <…...

为什么重写equals还要重写hashcode方法
目录equals方法hashCode方法为什么要一起重写?总结面试如何回答重写 equals 时为什么一定要重写 hashCode?要想了解这个问题的根本原因,我们还得先从这两个方法开始说起。 以下是关于hashcode的一些规定: 两个对象相等࿰…...
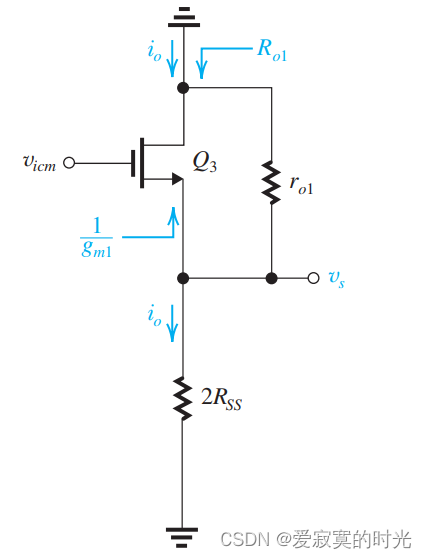
电子技术——电流镜负载的差分放大器
电子技术——电流镜负载的差分放大器 目前我们学习的差分放大器都是使用的是差分输出的方式,即在两个漏极之间获取电压。差分输出主要有以下优势: 降低了共模信号的增益,提高了共模抑制比。降低了输入偏移电压。提升了差分输入的增益。 由于…...

go面试题
1.json包在使用的时候,结构体里的变量不加tag能不能正常转成json里的字段? 如果变量首字母小写,则为private。无论如何不能转,因为取不到反射信息。如果变量首字母大写,则为public。 不加tag,可以正常转为j…...

攻防世界-Confusion1
题目 访问题目场景 某天,Bob说:PHP是最好的语言,但是Alice不赞同。所以Alice编写了这个网站证明。在她还没有写完的时候,我发现其存在问题。(请不要使用扫描器) 然后结合图片我们知道,这个网址是python写的࿰…...

机器学习实战--梯度下降法进行波士顿房价预测
前言: Hello大家好,我是Dream。 今天来学习一下如何使用机器学习梯度下降法进行波士顿房价预测,这是简单的一个demo,主要展示的是一些小小的思路~ 本文目录:一、波士顿房价预测1.全部的数据可视化2.地理数据可视化3.房…...

黑马】后台管理-项目优化和上线
一。项目优化优化1,加载进度条显示安装一个运行依赖,nprogress然后导包,调用对象展示和隐藏在main中基于拦截器实现展示进度条和隐藏进度条的效果如果触发请求拦截器,证明发起请求,希望展示进度条,如果触发…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
