Python数组仿射变换
文章目录
- 仿射变换
- 坐标变换的逻辑
- scipy实现
仿射变换
前面提到的平移、旋转以及缩放,都可以通过一个变换矩阵来实现,以二维空间中的变换矩阵为例,记点的坐标向量为 ( x , y , 1 ) (x,y,1) (x,y,1),则平移矩阵可表示为
[ 1 0 T x 0 1 T y 0 0 1 ] \begin{bmatrix} 1&0&T_x\\0&1&T_y\\0&0&1 \end{bmatrix} 100010TxTy1
旋转矩阵可表示为
[ cos θ sin θ − sin θ cos θ ] \begin{bmatrix} \cos\theta&\sin\theta\\-\sin\theta&\cos\theta \end{bmatrix} [cosθ−sinθsinθcosθ]
在scipy.ndimage中,提供了专门的仿射变换函数affine_transform,用于坐标的仿射变换。
坐标变换的逻辑
假设现在有一个矩阵
[ a b c d ] \begin{bmatrix}a&b\\c&d\end{bmatrix} [acbd]
则 a , b , c , d a,b,c,d a,b,c,d的坐标为 ( 0 , 0 ) , ( 1 , 0 ) , ( 0 , 1 ) , ( 1 , 1 ) (0,0),(1,0),(0,1),(1,1) (0,0),(1,0),(0,1),(1,1),那么假设现在给出一个变换矩阵
M = [ 1 1 1 1 ] M=\begin{bmatrix}1&1\\1&1\end{bmatrix} M=[1111]
则坐标 ( 0 , 1 ) (0,1) (0,1)变为
[ 0 1 ] [ 1 1 1 1 ] = [ 1 1 ] \begin{bmatrix}0&1\end{bmatrix}\begin{bmatrix}1&1\\1&1\end{bmatrix}=\begin{bmatrix}1&1\end{bmatrix} [01][1111]=[11]
从而 ( 1 , 1 ) (1,1) (1,1)处的值变为 c c c。另一方面 ( 1 , 0 ) (1,0) (1,0)坐标也变为 ( 1 , 1 ) (1,1) (1,1),所以 ( 1 , 1 ) (1,1) (1,1)处也可能为 b b b。
scipy实现
仿射变换函数支持output, order, mode, cval以及prefilter这5个参数,此外,二者均支持output_shape参数,用于调整输出的数组维度。除了这些参数之外,仿射变换的定义式为affine_transform(input, matrix, offset=0.0, ),其中matrix为变换矩阵,当输入不同维度的矩阵时,含义不同,设 n n n为输入数组的维度,则matrix的矩阵维度及其含义如下
- n × n n\times n n×n 对每一个输出轴进行线性变换
- ( n + 1 ) × ( n + 1 ) (n+1)\times (n+1) (n+1)×(n+1) 此时,
offset参数将不起作用,相当于把最后一个维度的参数作为偏移量 - n × ( n + 1 ) n\times (n+1) n×(n+1)
offset参数亦不起作用,但相当于最后一行的偏移量设为0。 - n n n 输入为一个向量,表示进行针对对角线的变换
下面仍以对仿射变换进行一个演示
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import *ori = np.eye(20)
ori[10, :] = 1.0a,b = 0.9,1.1
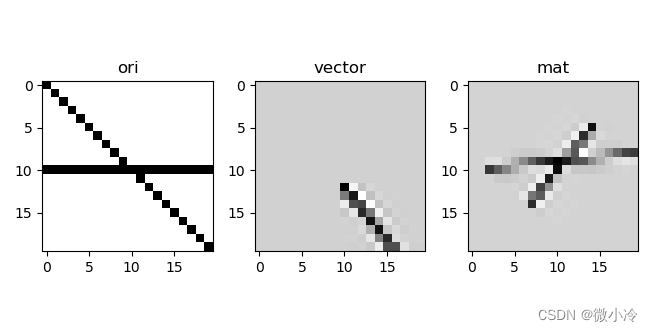
fDct = {"ori" : ori,"vector" : affine_transform(ori, [a, b], offset=(-10,-10)),"mat" : affine_transform(ori, [[a, b],[-b, a]], offset=(-10,10)),
}fig = plt.figure()
for i, key in enumerate(fDct):fig.add_subplot(1, 3, i+1)plt.imshow(fDct[key], cmap='gray_r')plt.title(key)plt.show()
效果如下
相关文章:

Python数组仿射变换
文章目录 仿射变换坐标变换的逻辑scipy实现 仿射变换 前面提到的平移、旋转以及缩放,都可以通过一个变换矩阵来实现,以二维空间中的变换矩阵为例,记点的坐标向量为 ( x , y , 1 ) (x,y,1) (x,y,1),则平移矩阵可表示为 [ 1 0 T x …...

“==“和equals方法究竟有什么区别?
操作符专门用来比较两个变量的值是否相等,也就是用于比较变量所对应的内存中所存储的数值是否相同,要比较两个基本类型的数据或两个引用变量是否相等,只能用操作符。 如果一个变量指向的数据是对象类型的,那么,这时候…...
蓝桥杯15单片机--超声波模块
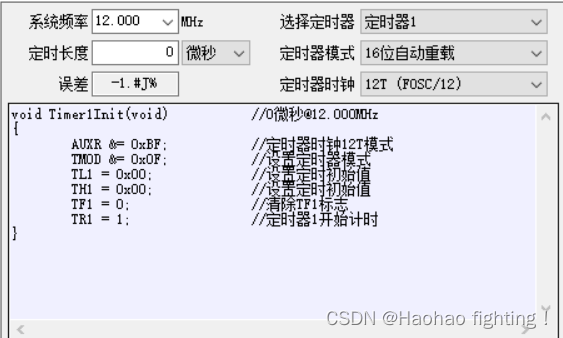
目录 一、超声波工作原理 二、超声波电路图 三、程序设计 1-设计思路 2-具体实现 四、程序源码 一、超声波工作原理 超声波时间差测距原理超声波发射器向某一方向发射超声波,在发射时刻的同时开始计时,超声波在空气中传播,途中碰到障碍…...

【学习笔记】ARC159
D - LIS 2 因为没有让你求方案数,所以还是比较好做的。 如果每一个连续段都退化成一个点,那么答案就是直接求 L I S LIS LIS。 否则,假设我们选了一些连续段把它们拼起来形成答案,显然我们有 r i 1 ≥ l i r_{i1}\ge l_i ri1…...

2023/4/16总结
图的存储 链式前向星 链式前向星和邻接表很相似,只是存储方式变成了数组。 链式前向星一般要用到一个结构体数组和一个一维数组,结构体数组edges中包括三个变量。结构体数组的大小一般由边的大小决定。 edges数组中的to代表的是某条边的终点v。w代表的是这条边的…...

【剑指offer】常用的数据增强的方法
系列文章目录 BN层详解 梯度消失和梯度爆炸 交叉熵损失函数 反向传播 1*1卷积的作用 文章目录 系列文章目录常用的数据增强的方法示例代码 常用的数据增强的方法 数据增强是指通过对原始数据进行一系列变换来生成更多的训练数据,从而提高模型的泛化能力。常用的数…...

/lib/lsb/init-functions文件解析
零、背景 在玩AppArmor的时候涉及到了/etc/init.d/apparmor(无论是sudo /etc/init.d/apparmor start还是sudo systemctl start apparmor.service),而这个文件又涉及到了另一个文件、也就是本文的主角:/lib/lsb/init-functions。 …...

【ChatGPT】ChatGPT-5 强到什么地步?
Yan-英杰的主页 悟已往之不谏 知来者之可追 C程序员,2024届电子信息研究生 目录 ChatGPT-5 强到什么地步? 技术 深度学习模型的升级 更好的预测能力 自适应学习能力 特点 语言理解能力更强 自我修正和优化 更广泛的应用领域 应用 对话系统 智能写作…...
[ARM+Linux] 基于全志h616外设开发笔记
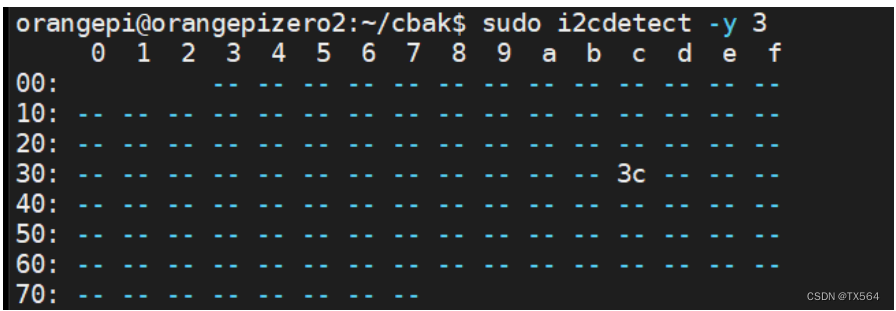
修改用户密码 配置网络 nmcli dev wifi 命令扫描周围WIFI热点 nmcli dev wifi connect xxx password xxx 命令连接WiFi 查看ip地址的指令: ifconfig ip addr show wlan0 SSH登录 这是企业开发调试必用方式,比串口来说不用接线,前提是接入网络…...
如何实现24小时客户服务
许多企业都有着这样的愿望:在不增加客服人员的同时能实现24小时客户服务。 那么有没有什么方法可以实现这一想法呢?在想解决方案之前我们可以先来谈谈客服的作用。 客服的作用主要为以下2点: 帮助用户更快地了解产品(减轻产品的…...
)
查询数据库空间(mysql和oracle)
Mysql版 1、查看所有数据库容量大小 -- 查看所有数据库容量大小 SELECTtable_schema AS 数据库,sum( table_rows ) AS 记录数,sum(TRUNCATE ( data_length / 1024 / 1024, 2 )) AS 数据容量(MB),sum(TRUNCATE ( index_length / 1024 / 1024, 2 )) AS 索引容量(MB) FROMinfor…...

为什么 SQLite 一定要用 C 语言来开发?
SQLite 是一种专门为在 Unix 和类 Unix 操作系统上运行的 Linux 服务器应用程序而设计的数据库管理系统,是一种轻量级的关系型数据库管理系统,它适用于许多嵌入式设备和物联网设备。它使用 C 语言编写,并且是一个开源项目。 简单易用&#x…...

TensorFlow Lite,ML Kit 和 Flutter 移动深度学习:6~11
原文:Mobile Deep Learning with TensorFlow Lite, ML Kit and Flutter 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的…...

你的GPT跟ChatGPT可能只差了一个DPU
“人类永远不会嫌网络太快,就像永远不会嫌高铁太快,你只会嫌它慢,希望它更快些。” 一个月内,百度、阿里、腾讯、商汤、讯飞、360等国内大厂扎堆发布“中国版 GPT ”,这家的名字还没记清楚,另一家的又蹦了出…...
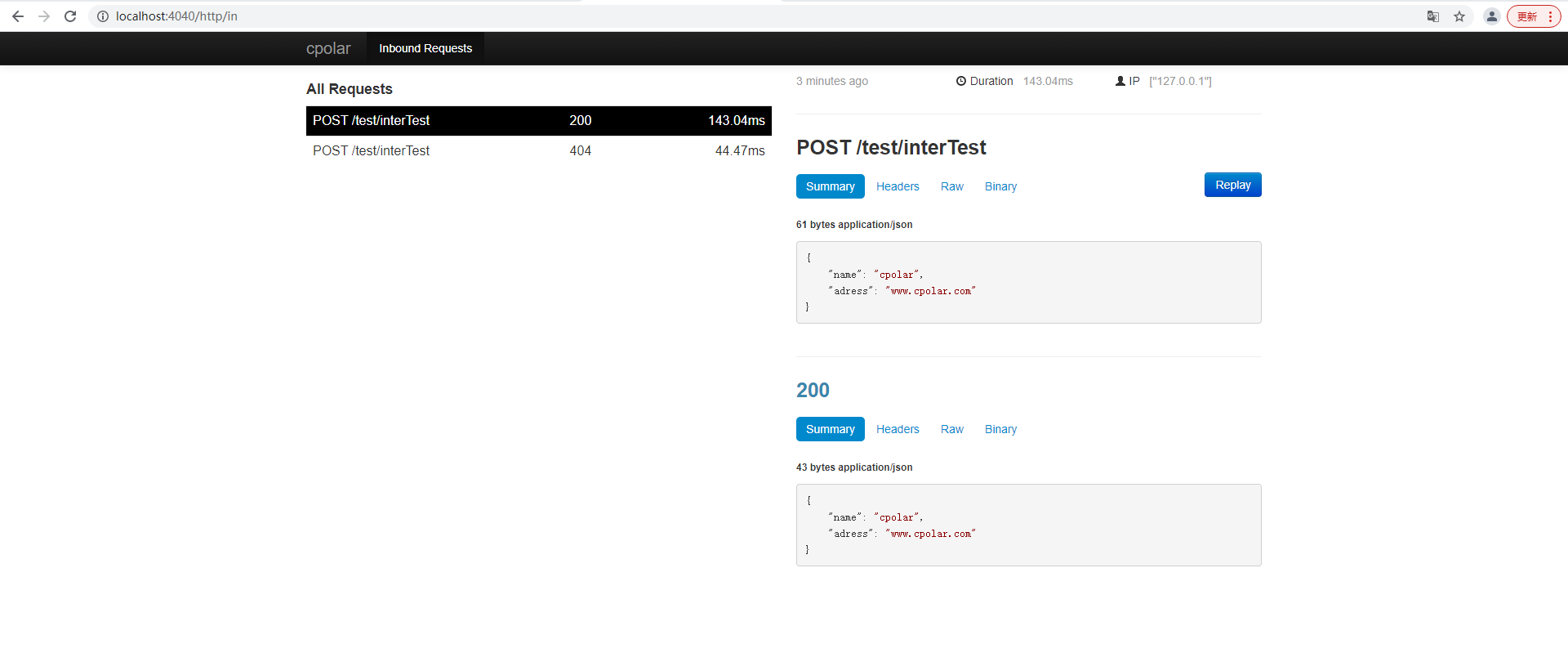
springboot服务端接口外网远程调试,并实现HTTP服务监听 - 内网穿透
文章目录 前言1. 本地环境搭建1.1 环境参数1.2 搭建springboot服务项目 2. 内网穿透2.1 安装配置cpolar内网穿透2.1.1 windows系统2.1.2 linux系统 2.2 创建隧道映射本地端口2.3 测试公网地址 3. 固定公网地址3.1 保留一个二级子域名3.2 配置二级子域名3.2 测试使用固定公网地址…...

NumPy的应用-1
准备工作 在Python中使用NumPy时,需要先安装NumPy。可以使用以下命令来安装NumPy: pip install numpy安装完成后,在Python中引入NumPy: import numpy as np安装完成并引入NumPy后,我们可以开始使用NumPy进行数据分析…...

k8s的yaml文件中kind类型详解
在Kubernetes(k8s)的YAML语法中,kind是一种重要的关键字,它用于指定Kubernetes资源的类型。根据Kubernetes官方文档,以下是kind可能的取值: Deployment:用于定义应用程序的声明式更新。Statefu…...

第三天:C语言控制结构
目录 1. 条件语句 2. 循环语句 3. 实例:计算阶乘 在前两天的学习中,您已经掌握了C语言的基本知识。今天,我们将学习C语言的控制结构,包括条件语句和循环语句。通过控制结构,您可以实现程序的分支和循环,…...
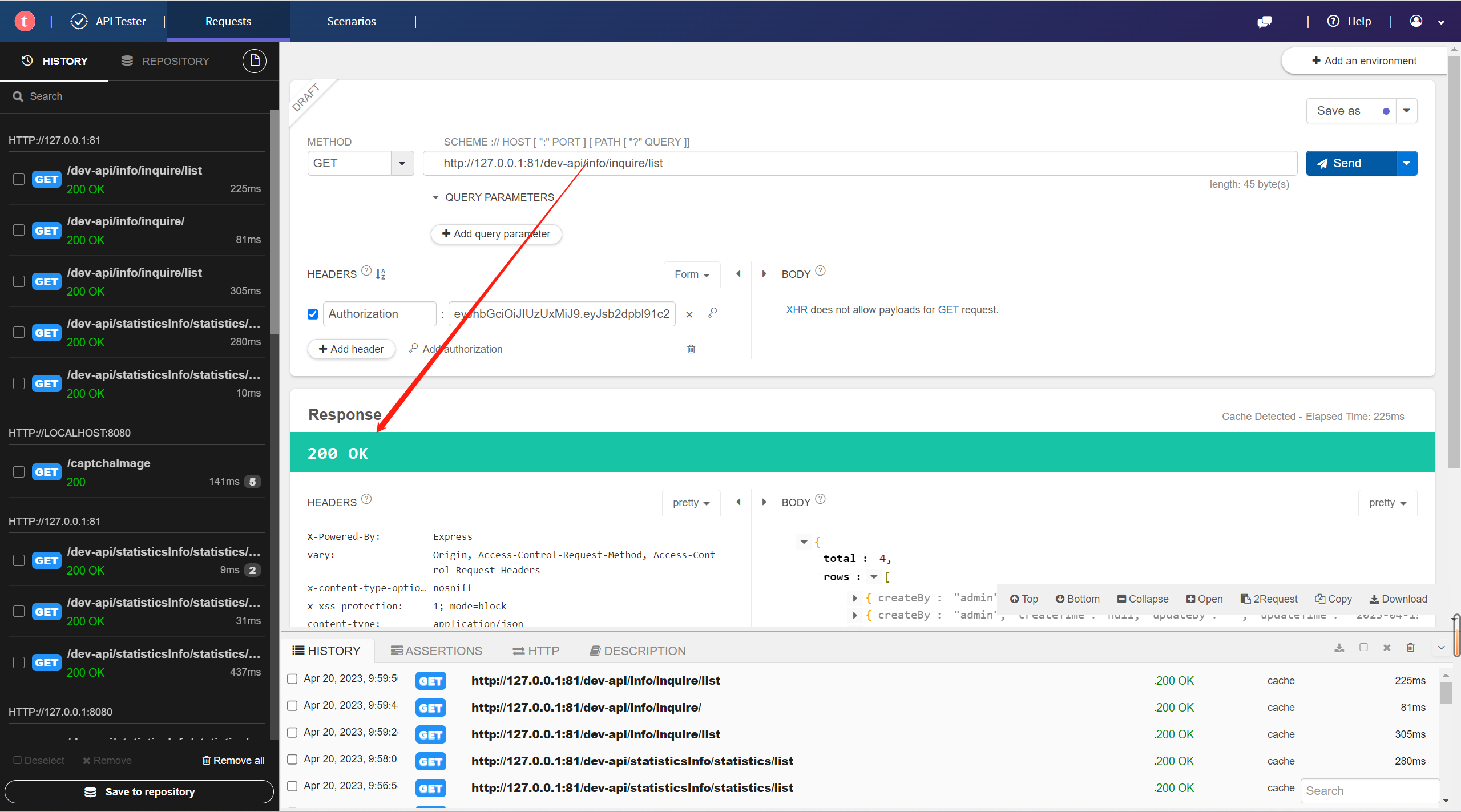
访问若依vue版后端api接口
访问若依vue版后端api接口 如何使用Talend API Tester进行访问若依vue-前后端分离版的后端api接口? 方法一: 写好一个后台api接口,启动项目 直接使用Talend API Tester进行访问后台api出现如下错误,原因是因为若依系统有jwt认证…...
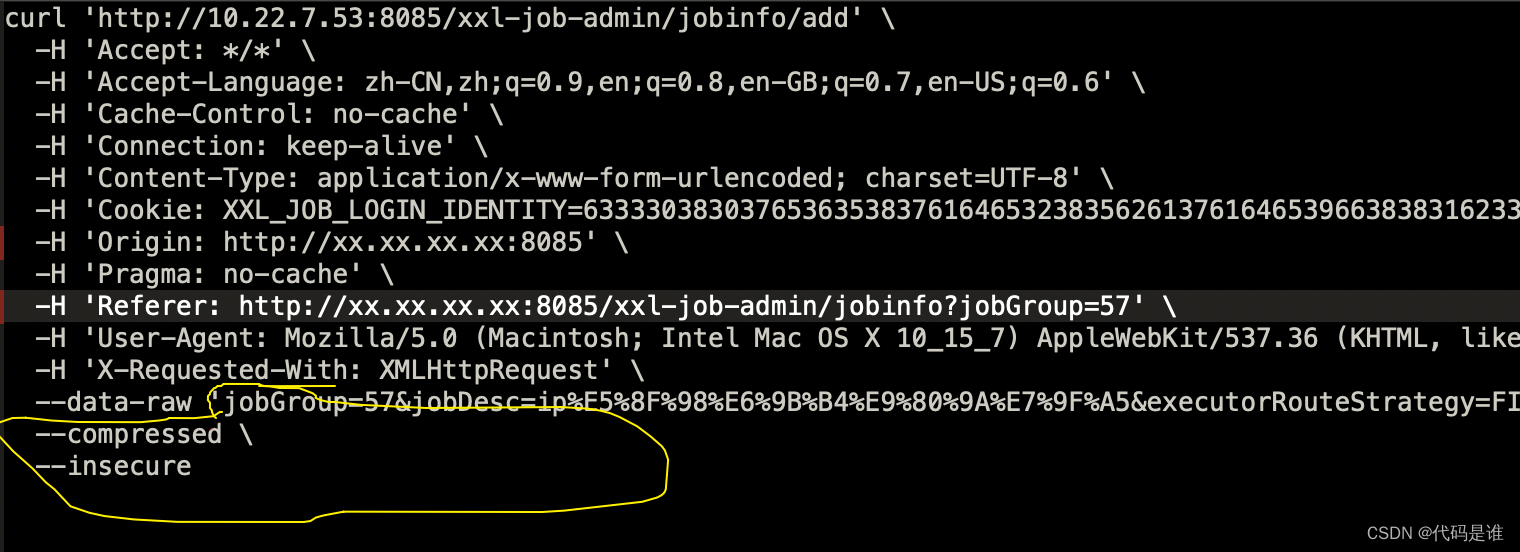
另一种迁移xxl-job任务的方法,适合不满足数据迁移条件
以为多个项目组同时使用一个xxl-job,同时涉及到版本提升,由此不太满足数据库数据迁移,所以这里提供另一种解决办法 使用工具:postman,json转excel,excel 核心:excel拼接: 1.使用f12抓取xxl任务访…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
