算法笔记-换根DP
换根DP
一般是给定一棵不定根树,求以每个节点为根的一些信息。可以通过二次扫描:
- 第一次扫描,任选一点为根,在有根树上,自底向上转移
- 第二次扫描,从上一次扫描的根开始,自顶向下计算
P3478 [POI2008] STA-Station
题意:
询问以哪个节点为根,所有节点的深度和最大。深度为到根节点的距离。
解析:
第一次扫描:以节点1为根(任意一个节点都可以),求出深度和。
第二次扫描:设第一次扫描时 v v v 是 u u u 的儿子。假设根节点由 u u u 变为 v v v , v v v 子树内所有节点的深度-1,不在 v v v 子树内的所有节点深度+1。 f v = f u − s i z e v + n − s i z e v f_v= f_u-size_v+n-size_v fv=fu−sizev+n−sizev, n n n 为所有节点数。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 1e6+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;struct edge{int to, nxt;
}e[maxn << 1];
int head[maxn], siz[maxn], tot, dep[maxn];
void add(int a, int b){e[++tot].nxt = head[a];e[tot].to = b;head[a] = tot;
}
int n, m;
ll f[maxn];
void dfs(int u, int fa){siz[u] = 1;dep[u] = dep[fa] + 1;for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa)continue;dfs(v, u);siz[u] += siz[v];}
}
void dfs2(int u, int fa){for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa)continue;f[v] = f[u] + n - siz[v] * 2;dfs2(v, u);}
}
signed main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i < n; i++){int u, v;cin >> u >> v;add(u, v); add(v, u);}dfs(1, 0);for(int i = 1; i <= n; i++)f[1] += dep[i];dfs2(1, 0);ll maxx = -1, res;for(int i = 1; i <= n; i++){if(maxx < f[i]){res = i;maxx = f[i];}}cout << res << endl;return 0;
}P2986 [USACO10MAR] Great Cow Gathering G
题意:
一棵树,边有边权,点有点权。询问以哪个点为根时, ∑ i = 1 n d i s ( i , r o o t ) ⋅ a i \sum\limits_{i=1}\limits^ndis(i, root) \cdot a_i i=1∑ndis(i,root)⋅ai。 a i a_i ai 为点权, d i s ( i , r o o t ) dis(i,root) dis(i,root) 为节点 i i i 与根节点的距离。
解析:
第一次扫描:
以1节点为根, f u f_u fu 表示 u u u 子树内节点到 u u u 距离点权的乘积的和。设 v v v 为 u u u 的儿子,则 f u = ∑ ( f v + s i z e v × e ( u , v ) ) f_u =\sum(f_v+size_v\times e(u,v)) fu=∑(fv+sizev×e(u,v)), e ( u , v ) e(u,v) e(u,v) 为 ( u , v ) (u,v) (u,v) 边的长度。
第二次扫描:
设第一次扫描时 v v v 是 u u u 的儿子。假设根节点由 u u u 变为 v v v, v v v 子树内所有节点到根节点的距离减小 e ( u , v ) e(u,v) e(u,v),不在 v v v 子树内的所有节点到根节点的距离增加 e ( u , v ) e(u,v) e(u,v)。 f v = f u + ( n − 2 × s i z e v ) × e ( u , v ) f_v= f_u+(n-2\times size_v)\times e(u,v) fv=fu+(n−2×sizev)×e(u,v), n n n 为所有节点数。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 1e6+10;
const ll INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int, int> pii;#define int ll
struct edge{int to, nxt, w;
}e[maxn << 1];
int head[maxn], siz[maxn], tot;
void add(int a, int b, int c){e[++tot].nxt = head[a];e[tot].to = b;e[tot].w = c;head[a] = tot;
}
int n, m;
ll f[maxn], a[maxn], sum;
void dfs(int u, int fa){siz[u] = a[u];for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa)continue;dfs(v, u);siz[u] += siz[v];f[u] += f[v] + siz[v] * e[i].w;}
}
void dfs2(int u, int fa){for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa)continue;f[v] = f[u] - siz[v] * e[i].w + (sum - siz[v]) * e[i].w;dfs2(v, u);}
}
signed main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];sum += a[i];}for(int i = 1; i < n; i++){int u, v, w;cin >> u >> v >> w;add(u, v, w); add(v, u, w);}dfs(1, 0);dfs2(1, 0);ll res = INF;for(int i = 1; i <= n; i++)res = min(res, f[i]);cout << res << endl;return 0;
}积蓄程度
题意:
一棵树,根节点可以流出无限水,叶子节点可以吸收无限水,每条边有流量限制。询问以哪个点为根节点时,叶子节点吸收的水最多。
解析:
第一次扫描:
令 f u f_u fu 为以1为根节点时,以 u u u 为根的子树中,吸收的水量。
设 v v v 为 u u u 的儿子:
{ f u + = m i n ( f v , w ( u , v ) ) , d e g v = 1 f u + = w ( u , v ) , d e g v ≠ 1 \begin{cases} f_u += min(f_v, w(u, v)), & deg_v = 1\\ f_u += w(u, v), & deg_v \neq 1 \end{cases} {fu+=min(fv,w(u,v)),fu+=w(u,v),degv=1degv=1
第二次扫描:
令 g u g_u gu 为以 u u u 为根节点时,最大流量。
设第一次扫描时 v v v 是 u u u 的儿子。假设根节点由 u u u 变为 v v v
g v g_v gv 包括两部分:
- 一部分是第一次扫描的 f v f_v fv
- 一部分是流向 u u u 进而流向其他节点
对 u u u 而言,从 u u u 到 v v v 的流量为 m i n ( f j , w ( i , j ) ) min(f_j, w(i,j)) min(fj,w(i,j)),流向 v v v 之外的流量为 g u − m i n ( f j , w ( i , j ) ) g_u - min(f_j, w(i,j)) gu−min(fj,w(i,j))。所以 g v g_v gv 的第二部分为 m i n ( w ( u , v ) , g u − m i n ( f j , w ( i , j ) ) ) min(w(u,v), g_u - min(f_j, w(i,j))) min(w(u,v),gu−min(fj,w(i,j)))。也需要按照度是否为1讨论一下: { g v = f v + w ( u , v ) d e g u = 1 g v = f v + m i n ( g u − w ( u , v ) , w ( u , v ) ) d e g u ≠ 1 , d e g v = 1 g v = f v + m i n ( g u − m i n ( f v , w ( u , v ) ) , w ( u , v ) ) , d e g u ≠ 1 , d e g v ≠ 1 \begin{cases} g_v = f_v+ w(u, v) & deg_u = 1\\ g_v = f_v + min(g_u-w(u,v), w(u, v)) °_u \neq 1 ,deg_v = 1\\ g_v = f_v + min(g_u-min(f_v, w(u,v)), w(u,v)),& deg_u \neq 1 ,deg_v \neq 1 \end{cases} ⎩ ⎨ ⎧gv=fv+w(u,v)gv=fv+min(gu−w(u,v),w(u,v))gv=fv+min(gu−min(fv,w(u,v)),w(u,v)),degu=1degu=1,degv=1degu=1,degv=1
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 2e5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;#define int ll
struct edge{int to, nxt, w;
}e[maxn << 1];
int head[maxn], siz[maxn], tot;
void add(int a, int b, int c){e[++tot].nxt = head[a];e[tot].to = b;e[tot].w = c;head[a] = tot;
}
int n, m;
ll f[maxn], g[maxn], deg[maxn];
void dfs(int u, int fa){f[u] = 0;for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa)continue;dfs(v, u);if(deg[v] == 1)f[u] += e[i].w;elsef[u] += min(e[i].w, f[v]);}
}
void dfs2(int u, int fa){for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa)continue;if(deg[u] == 1)g[v] = f[v] + e[i].w;else if(deg[v] == 1)g[v] = f[v] + min(g[u]-e[i].w, e[i].w);elseg[v] = f[v] + min(g[u]-min(f[v], e[i].w), e[i].w);dfs2(v, u);}
}
void solve(){cin >> n;memset(deg, 0, sizeof(deg));tot = 0;memset(head, 0, sizeof(head));for(int i = 1; i < n; i++){int a, b, c;cin >> a >> b >> c;add(a, b, c);add(b, a, c);deg[a]++; deg[b]++;}dfs(1, 0);g[1] = f[1];dfs2(1, 0);ll res = 0;for(int i = 1; i <= n; i++)res = max(res, g[i]);cout << res << endl;
}
signed main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);int T;cin >> T;while(T--)solve();return 0;
}相关文章:

算法笔记-换根DP
换根DP 一般是给定一棵不定根树,求以每个节点为根的一些信息。可以通过二次扫描: 第一次扫描,任选一点为根,在有根树上,自底向上转移第二次扫描,从上一次扫描的根开始,自顶向下计算 P3478 [P…...
LeetCode 785. Is Graph Bipartite【DFS,二分图】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【微信小程序】-- 分包 - 独立分包 分包预下载(四十五)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

2.3 连续性随机变量
思维导图: 学习目标: 我会按照以下步骤学习连续型随机变量: 复习概率论的基础知识,包括概率、期望、方差等概念和公式,以及离散型随机变量的概率分布函数和概率质量函数的概念和性质。 学习连续型随机变量的概念和性…...
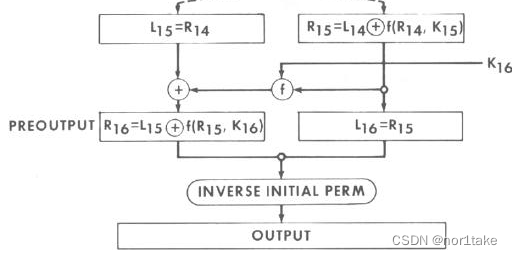
【DES详解】(一)处理input block(64 bits)
一、DES 加密算法总览 0-1、初识置换 IP(Initial Permutation) 输入:明文(64 bits) 过程:初识置换 输出:处理后的明文permuted input(64 bits) 首先,对需要解…...

redis笔记——三种特殊的数据结构
三种特殊数据类型 geospatial(地理位置) 用于定位,附近的人,距离计算 添加元素 geoadd key 经度 纬度 描述名称,可一次添加多个元素 127.0.0.1:6379> geoadd china:city 113.28 23.12 guangzhou (integer) 1 1…...

网络安全之编码加密算法
网络安全之编码加密算法 一、ROT5/13/18/47编码转换二、MD5加密 一、ROT5/13/18/47编码转换 ROT5、ROT13、ROT18、ROT47 编码是一种简单的码元位置顺序替换暗码,属于凯撒密码的一种。此类编码具有可逆性,可以自我解密,主要用于应对快速浏览&…...

mp4视频无法播放的解决方法
mp4视频是我们日常工作生活中经常会遇到的视频格式,但如果遇到重要的mp4视频无法播放了,该怎么办呢?有mp4视频无法播放的解决方法吗?下面小编为大家整理了这个问题产生的原因以及相应的解决方法,让我们看一看。 什么情况下会导致mp4视频无法…...

搭建Mysql
登录root账号 su root #上传 mysql-advanced-5.7.17-linux-glibc2.5-x86_64.tar.gz #创建mysql的用户组/用户, data目录及其用户目录 groupadd mysql useradd -g mysql -d /home/mysql mysql mv mysql-advanced-5.7.17-linux-glibc2.5-x86_64 mysql mkdir /home/mysql/data…...

气传导和骨传导耳机哪个好?简单科普这两种蓝牙耳机
在生活中,我们经常会用到耳机,特别是在日常娱乐听歌、运动休闲、户外通勤的时候,一款舒适的耳机是必不可少的。 而最近几年,随着科技的发展,各大品牌也相继推出了各种类型的耳机,其中比较热门的就有气传导…...
浅尝GoWeb开发之Gin框架
一、框架简介 gin 目前应用最广泛的golang框架,甚至已经变成了golang的官方框架,但它主要是一个RESTFul的框架。封装比较优雅,API友好,源码注释比较明确。个人比较推荐。 beego 国内最早的golang框架,也是最全的MV…...

工程行业管理系统-专业的工程管理软件-提供一站式服务
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示1…...
目标检测YOLO系列-YOLOV7运行步骤(推理、训练全过程)
下载源代码:点击下载 进入项目根目录并执行以下命令安装requirements.txt中的相关依赖 pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple官网下载权重yolov7.pt(测试使用)、yolov7-tiny.pt(训练使用…...
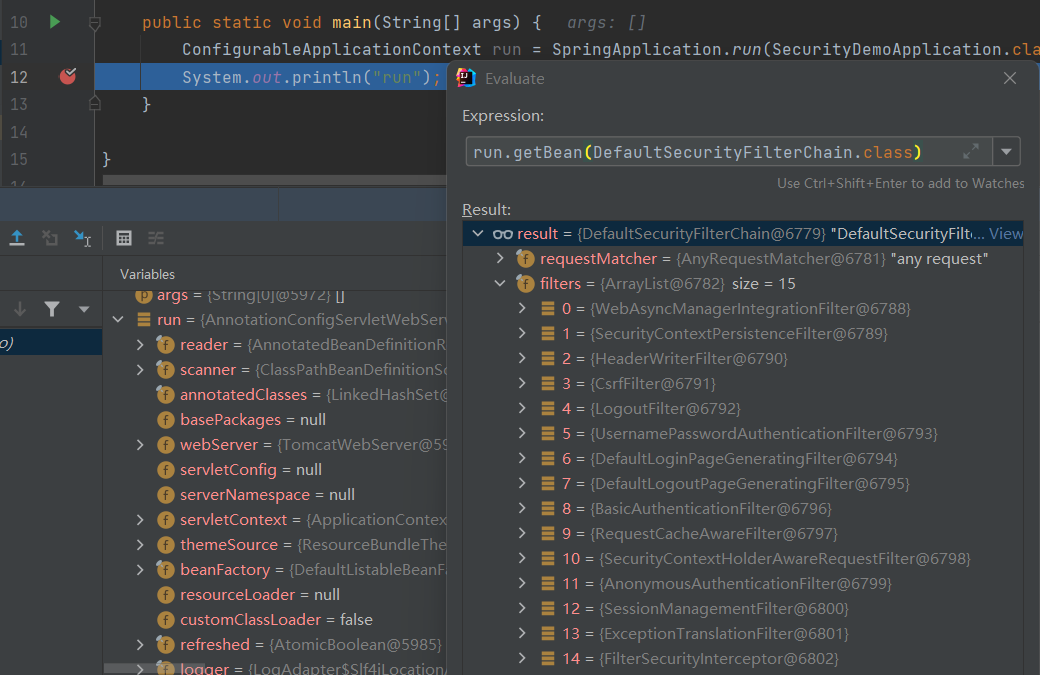
Spring Boot + Spring Security基础入门教程
Spring Security简介 Spring Security 是一个功能强大且高度可定制的身份验证和访问控制框架。Spring Security 致力于为 Java 应用程序提供身份验证和授权的能力。 Spring Security 两大重要核心功能:用户认证(Authentication)和用户授权&am…...

MySQL数据库,表的增删改查详细讲解
目录 1.CRUD 2.增加数据 2.1创建数据 2.2插入数据 2.2.1单行插入 2.2.2多行插入 3.查找数据 3.1全列查询 3.2指定列查询 3.3查询字段为表达式 3.3.1表达式不包含字段 3.3.2表达式包含一个字段 3.3.3表达式包含多个字段 3.4起别名 3.5distinct(去重) 3.6order …...
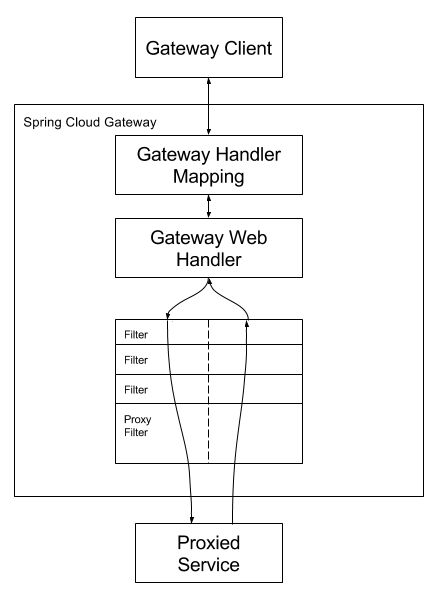
SpringCloud-Gateway实现网关
网关作为流量的入口,常用的功能包括路由转发、权限校验、限流等 Spring Cloud 是Spring官方推出的第二代网关框架,由WebFluxNettyReactor实现的响应式的API网关,它不能在传统的servlet容器工作,也不能构建war包。基于Filter的方式…...

Redis 如何配置读写分离架构(主从复制)?
文章目录 Redis 如何配置读写分离架构(主从复制)?什么是 Redis 主从复制?如何配置主从复制架构?配置环境安装 Redis 步骤 通过命令行配置从节点通过配置文件配置从节点Redis 主从复制优点Redis 主从复制缺点 Redis 如何…...

代码随想录二刷day05 | 哈希表之242.有效的字母异位词 349. 两个数组的交集 202. 快乐数 1. 两数之和
当遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法了 二刷day05 242.有效的字母异位词349. 两个数组的交集202. 快乐数1. 两数之和 242.有效的字母异位词 题目链接 解题思路: class Solution { public:bool isAnagram(string s, string…...

2023年4月广东省计算机软考中/高级备考班招生简章
软考是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资格考试。 系统集成…...
在Github中77k星的王炸AutoGPT,会独立思考,直接释放双手
文章目录 1 前言1.1 什么是AutoGPT1.2 为什么是AutoGPT 2 AutoGPT部分实例2.1 类似一个Workflow2.2 市场调研2.3 自己写播客2.4 接入客服 3 安装和使用AutoGPT3.1 安装3.2 基础用法3.3 配置OpenAI的API3.4 配置谷歌API3.5 配置Pinecone API 4.讨论 1 前言 迄今为止,…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
