二叉排序树(二叉查找树)基本操作_20230417
二叉排序树(二叉查找树)基本操作_20230417
- 前言
二叉排序树首先是一颗二叉树,它不同于常规二叉树的地方在于,如果左子树不为空,那么左子树上所有结点的值都不大于根节点的值,如果右子树不为空,那么右子树上所有的值不小于根节点的值,而且它的左右子树本身也属于二叉排序树。
二叉排序树的形式和元素的输入顺序相关,它最坏的情况下可能退化为有序线性表。大多数条件下,二叉排序树既具备二叉树的折半查找行者,又采用了链表作为储存结构,加强了数据储存的灵活性,不失为一种优秀的数据储存结构。
下面的二叉排序树通过中序遍历,就得到一组有序表。

- 二叉排序树的基本操作
2.1 查找操作
二叉排序树的查找操作操作可通过递归实现,由于二叉排序树当中的每个元素都包含有数据域、左孩子指针和右孩子指针,通过递归可以定位到是在左孩子还是右孩子区域进行查找。如果元素比对成功,则返回 true;如果查找失败,则返回false. 如果查找成功,其中的某个递归变量保留查找成功的结点,如果没有找到目标元素,则某个递归变量保留此元素的根节点(父节点)的位置。
查找的实际上是沿着根节点往下遍历的过程,它会形成一颗合适的遍历路径,如果配对成功,路径上的结点都是目标结点的父节点。
看一个具体的例子。给点上述二叉排序树,要求查找元素的值为30,那么遍历形成路径用绿色虚线表示,遍历经过了左–>左–>右的路径。

元素查找的实现, 如果发现递归结点已经为NULL,意识是查询失败,此二叉排序树当中不含有目标元素,此时查找目标赋值为待查找元素的父节点,同时返回查询失败标记false, false会在退栈过程中不断传递给当前的栈,最终查找函数返回false.
同时,如果当前结点的值和待查找的值相等,意味着本次查询成功,递归可以结束(不再入函数栈),同时返回查询成功的标记true,true会在退栈过程中不断传递给上一级函数栈,最终查找函数返回true。
typedef struct BiTNode
{SElemType data;struct BiTNode *lchild;struct BiTNode *rchild;
} BiTNode, *BiTree;bool find_bst(BiTree T, KeyType key, BiTree parent, BiTree *target_ptr)
{if(T==NULL){*target_ptr=parent;return false; //one of termination conditions, traveling with parent}else{//another condition of termination conditions//traveling with parentif(EQ(key,T->data.key)) {*target_ptr=T;return true;}else if (LT(key, T->data.key)){return find_bst(T->lchild,key,T,target_ptr);}else{return find_bst(T->rchild,key,T,target_ptr);}}
}
2.2 插入和创建树操作
二叉排序树是一类动态表,其原因在于,如果树中不含有待插入元素,那么二叉排序树会执行插入操作,从而达到动态更新表的目的。插入和创建实际上可以共用一个过程,插入的过程也是创建树的过程。利用上面的查找函数,可以实现插入的过程。正如前面所述,插入过程需要先判断待插入元素是否在现有的表当中,如果不包含在目前的表当中,则需要执行插入操作,并返回插入成功的标记true,否则则直接返回未执行插入的标记false.
bool insert_bst(BiTree *bt, KeyType key)
{BiTree ptr;BiTree new_node;if(!find_bst(*bt,key,NULL,&ptr)){new_node=(BiTree)malloc(sizeof(BiTNode));new_node->data.key=key;new_node->data.value=NULL;new_node->lchild=NULL;new_node->rchild=NULL;if(ptr==NULL) // don't leave this condition behind{*bt=new_node;}else if(LT(key,ptr->data.key)){ptr->lchild=new_node;}else{ptr->rchild=new_node;}return true;}return false;
}
2.3 二叉排序树删除操作
二叉排序树的结点删除分3种情况讨论,
a.) 若P为叶子结点,既PL和PR均为空树,由于删除叶子结点不破坏树的结点,只需要修改P结点的指针即可,也就是*p=NULL即可。

b.) 上述图,若 P结点只有左子树或只有右子树,此时只要令PL或PR称为父节点的左子树即可(也即是把指针赋值为结点P即可)
c.) 若P结点的左右子树均不为空,如果删除元素P后,需要保持二拆排序树仍然有序,那么就有两种途径,①-a途径,称之为替代法,用p元素的直接前驱元素S里面的值替代P里面的值,P的左右孩子指针保持不变,同时删除S结点,把S结点的左孩子赋值给其双亲结点的右孩子;②-b途径是利用待删除元素的左子树根节点来替代P所在结点,同时把P结点原有的右子树赋值给左子树的最右端元素。
两种类型不同在于①-a利用原有结点的左右孩子指针,只是替代元素;②-b则是直接修改替换原有结点,并更新现有结点的对应指针。

c) 删除的代码实现
二叉排序树的删除过程仍然采用递归函数,如果找到待删除元素,则执行删除操作,并返回删除成功标记,否则返回删除失败标记。
bool delete_bst(BiTree *T, KeyType key)
{//if deletion is succesfful, it will return true;//if deletion is not successful, it will return falseif(*T==NULL){return false; // one termination condition}else{if(EQ(key,(*T)->data.key)){delete_action_b(T); //propagate the return valuereturn true; //the second termination condition}else if (LT(key, (*T)->data.key)){return delete_bst(&((*T)->lchild),key);}else{return delete_bst(&((*T)->rchild), key);}}
}
分别用两个函数实现不同的删除模式,
//①-a implementation code
void delete_action_a(BiTree *node)
{//p;//s;//list three scenarios of nodeBiTree p;BiTree s;if((*node)->lchild==NULL){p=*node;(*node)=(*node)->rchild;free(p);}else if ((*node)->rchild == NULL){p = *node;(*node) = (*node)->lchild;free(p);}else{p= *node;s=(*node)->lchild; //next onewhile(s->rchild!=NULL){p=s;s=s->rchild;}(*node)->data=s->data;if(p!=(*node)){p->rchild=s->lchild;}else{p->lchild=s->lchild; //no right child and jumpt one node}free(s);}return;
}//②-b implementation code
void delete_action_b(BiTree *node)
{BiTree p;BiTree s;if ((*node)->lchild == NULL){p = *node;(*node) = (*node)->rchild;free(p);}else if ((*node)->rchild == NULL){p = *node;(*node) = (*node)->lchild;free(p);}else{p = *node;s = (*node)->lchild;while (s->rchild != NULL){s = s->rchild;}s->rchild=(*node)->rchild; // 先后顺序非常重要(*node)=(*node)->lchild; // 先后顺序非常重要free(p);}return;
}
- 二叉查找树的形式
与静态二叉搜索树不同,静态二叉搜索树的形式是唯一的;对于相同的元素集合,二叉查找树的形式会随着不同的排列顺序呈现不同的树的形态。由于树的形态不同,造成树的深度不同,导致平均查找长度不同(Average Search Length),如果输入有序元素,二叉查找树就退化为有序线性表,导致极端的情况发生。

这就为后面平衡二叉查找树的引入提供了应用场景,本文仅针对二叉排序树,不会对AVL树进一步阐述。
- 小结
本文学习了二叉排序树的不同操作,包括插入、建树和删除等操作,同时阐述了不同形态的二叉查找树会影响查找效率,极端情况下,有序输入会导致二叉排序树蜕变为线性表,严重影查询效率。
参考资料:
《数据结构》严蔚敏,清华大学
相关文章:

二叉排序树(二叉查找树)基本操作_20230417
二叉排序树(二叉查找树)基本操作_20230417 前言 二叉排序树首先是一颗二叉树,它不同于常规二叉树的地方在于,如果左子树不为空,那么左子树上所有结点的值都不大于根节点的值,如果右子树不为空,…...
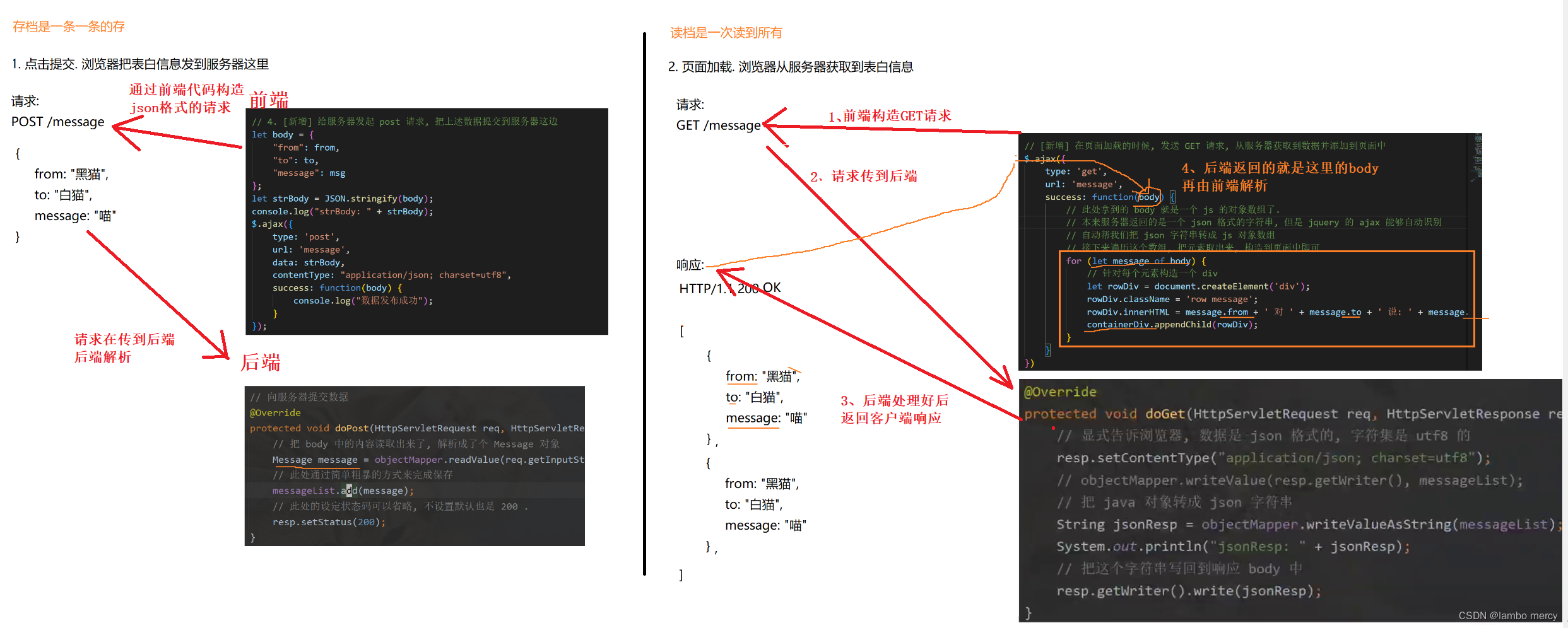
实现服务器版本的表白墙
目录 初始前端代码 网页初始效果 一、确定接口 二、编写代码 2.1 创建项目七步走 1、创建Maven项目 2、引入依赖 3、构建目录 4、编写代码 5、打包、部署 编辑 7、验证代码 三、具体的代码逻辑 3.1 服务器——两个服务接口 3.2 前端页面的代码 3.2.1 前端存档…...

TensorFlow 2 和 Keras 高级深度学习:6~10
原文:Advanced Deep Learning with TensorFlow 2 and Keras 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象&#x…...

unity,制作一个环状滑动条
介绍 unity,制作一个环状滑动条 方法 1.导入png图片素材2.新建一个滑动条,两者图片都设置为图片3.调节slider的参数4.调节backgroud的参数5.fill area、fill的参数同上。 得到两个叠加的圆环。6.设置fill的背景颜色为红色7.设置fill填充方式࿰…...

2023-04-17 算法面试中常见的树和递归问题
二叉树和递归 0 LeetCode297 二叉树的序列化和反序列化 序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据…...

3分钟通过日志定位bug,这个技能测试人必须会
♥ 前 言 软件开发中通过日志记录程序的运行情况是一个开发的好习惯,对于错误排查和系统运维都有很大帮助。 Python 标准库自带了强大的 logging 日志模块,在各种 python 模块中得到广泛应用。 一、简单使用 1. 入门小案例 import logging logging.ba…...
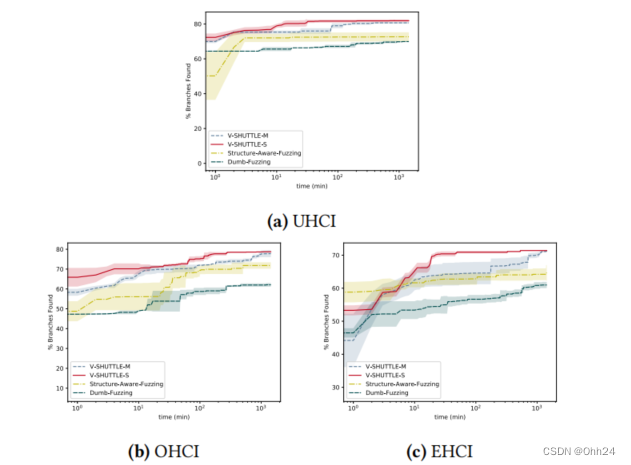
【论文总结】V-Shuttle:可扩展和语义感知的 Hypervisor 虚拟设备模糊测试
介绍 这是来自2021 CCS的一篇论文,作者有GaoningPan, Xingwei Lin, Xuhong Zhang, Yongkang Jia, Shouling Ji, Chunming Wu, Xinlei Ying, Jiashui Wang, Yanjun Wu。该论文提出V-shuttle的新框架来执行管控程序的模糊测试,该框架执行可扩展和语义感知…...

一篇文章让你搞懂TypeScript中的typeof()、keyof()是什么意思
TypeScript中的typeof()、keyof()是什么意思? 知识回调(不懂就看这儿!)场景复现核心干货👇👇👇举例引入字面量类型(literal types&…...
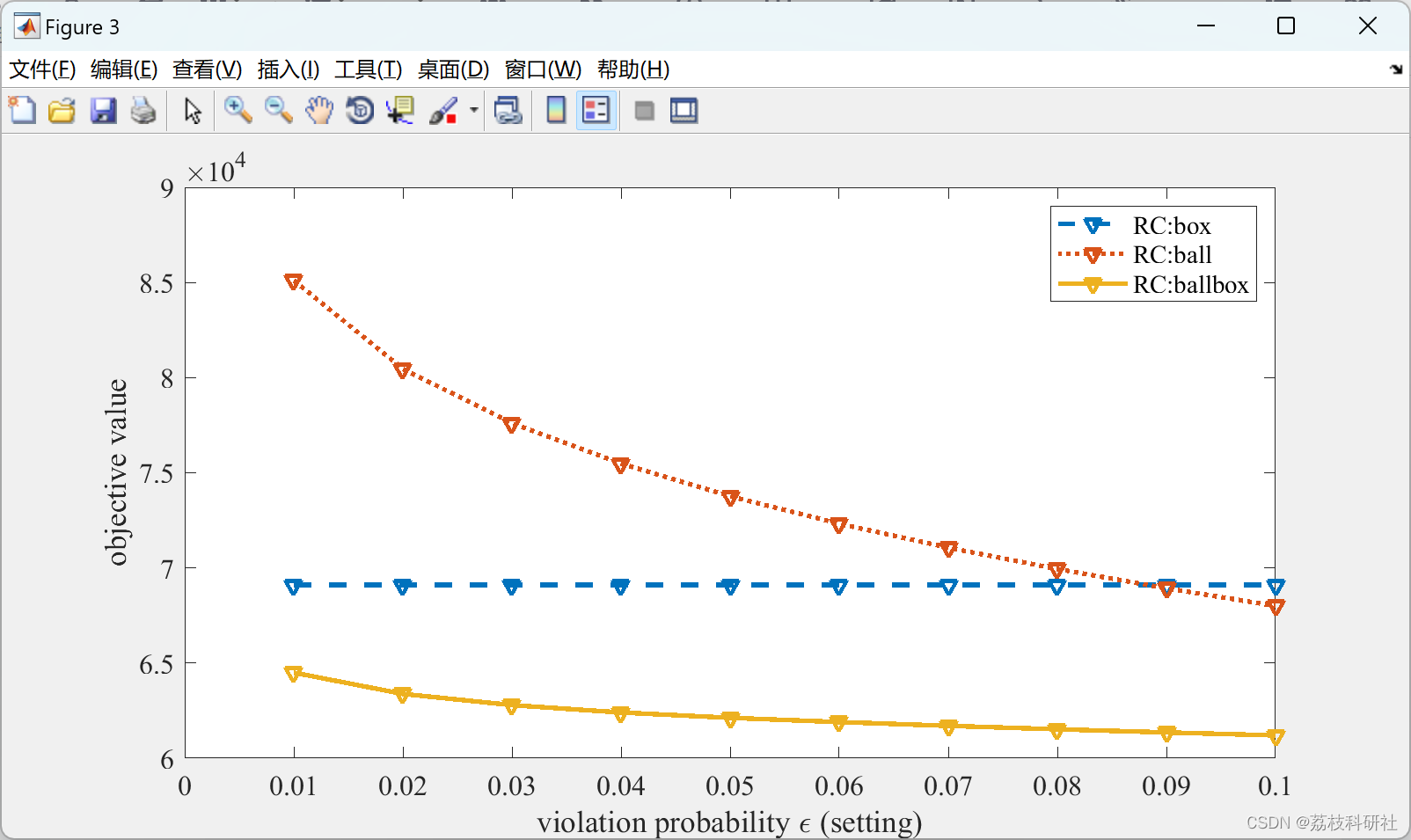
【机会约束、鲁棒优化】机会约束和鲁棒优化研究优化【ccDCOPF】研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

4月想跳槽的同学,没有更好的选择,可以去美团
在美团干了半年,说一下自己的感受,美团是一家福利中等,工资待遇中上,高层管理团队强大,加班强度一般,技术不错,办公环境一般,工作氛围中上,部门差距之间工作体验差距巨大…...
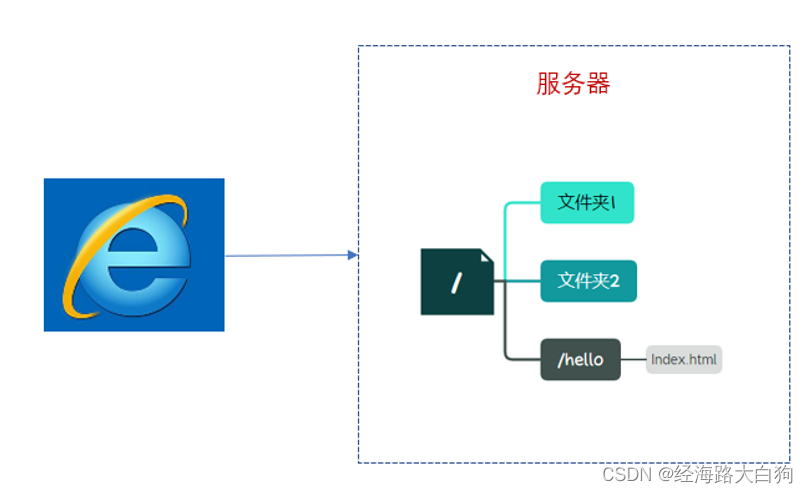
从输入url到页面展现(一)从浏览器解析url开始
前端面试有一道很考验人的问题,那就是:请你说一下从用户从输入url到页面展现的过程是怎样的?在接下来的一段时间呢,狗哥会从这一问题出发,开始剖析这个过程,希望可以让更多的小伙伴掌握到这个过程ÿ…...

购物 · 礼物
标题 前言必学场景词汇及用法书店花店玩具店讨价还价情境常用单词书店花店玩具店前言 加油 必学场景词汇及用法 书店 1.book store / book shop 书店 I browsed through the book store, but I didn’t find the book I was looking for. 我把书店里的书浏览了一番,但是没…...
)
可视化图表API格式要求有哪些?Sugar BI详细代码示例(2)
Sugar BI中的每个图表可以对应一个数据 API,用户浏览报表时,选定一定的过滤条件,点击「查询」按钮将会通过 API 拉取相应的数据;前面说过,为了确保用户数据的安全性,Sugar BI上的所有数据请求都在Sugar BI的…...
153. 寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2] 若旋转 7 次࿰…...
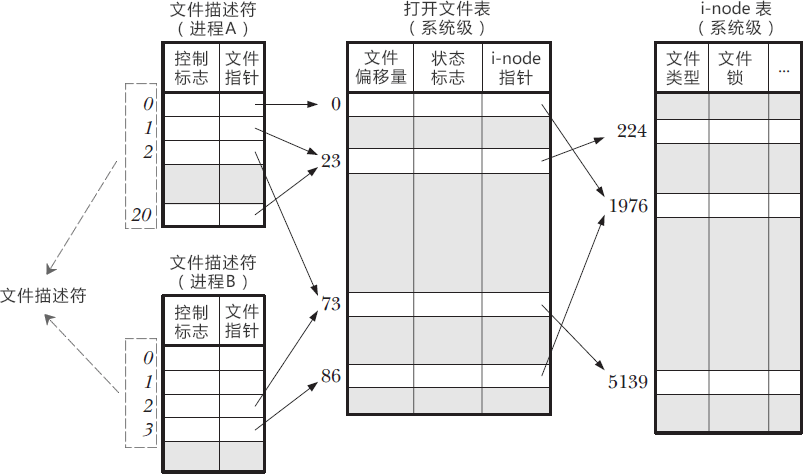
Linux 文件描述符
Linux 文件描述符 Linux 中一切皆文件,比如 C 源文件、视频文件、Shell脚本、可执行文件等,就连键盘、显示器、鼠标等硬件设备也都是文件。 一个 Linux 进程可以打开成百上千个文件,为了表示和区分已经打开的文件,Linux 会给每个…...

第17章_反射机制
第17章_反射机制 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 1. 反射(Reflection)的概念 1.1 反射的出现背景 Java程序中,所有的对象都有两种类型:编…...

使用VBA小程序提高资产清查效率
资产清查是一件相当烦人的工作,去年使用LayUIPHPMS SQL Server 2014写了一个资产清查的程序,可惜写完了,LayUI已经停止更新了,就没有再完善下去,数据也没有更新,等于就废了。 今年又要进行资产清查…...

JavaSE学习进阶day07_02 异常
第三章 异常 3.1 异常概念 异常,就是不正常的意思。在生活中:医生说,你的身体某个部位有异常,该部位和正常相比有点不同,该部位的功能将受影响.在程序中的意思就是: 异常 :指的是程序在执行过程中,出现的非正常的情况࿰…...
操作系统学习笔记
文章目录 操作系统虚拟内存锁缓存机制CPU性能指标进程、线程文件管理系统 操作系统 操作系统是控制应用程序的执行,并充当应用程序和计算机硬件之间的接口。在计算机系统中,处于最外层的是(应用软件) 。 面向用户的就是外层的&am…...

【Spring Boot】SpringBoot设计了哪些可拓展的机制?
文章目录 前言SpringBoot核心源码拓展Initializer拓展监听器ApplicationListenerBeanFactory的后置处理器 & Bean的后置处理器AOP其他的拓展点 前言 当我们引入注册中心的依赖,比如nacos的时候,当我们启动springboot,这个服务就会根据配置…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
