代码随想录NO42 | 动态规划_Leetcode70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数
动态规划_Leetcode70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数
70. 爬楼梯 (进阶)
在原题基础上,改为:一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
1阶,2阶,… m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
- 1.确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。 - 2.确定递推公式
本题dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j] - 3.dp数组如何初始化、
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
下标非0的dp[i]初始化为0,因为dp[i]是靠dp[i-j]累计上来的,dp[i]本身为0这样才不会影响结果。 - 4.确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
所以需将target放在外循环,将nums放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。 - 5. 举例来推导dp数组
class Solution:def climbStairs(self, n: int) -> int:dp = [0]*(n+1)dp[0] = 1for i in range(n+1):for j in range(1,m+1):if i - j >= 0:dp[i] += dp[i-j]return dp[-1]
把代码中的m替换为2,即为本题的完全背包解法。
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
思路:题目中说每种硬币的数量是无限的,可以看出是典型的完全背包问题。
动规五部曲分析如下:
- 1.确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j] - 2.确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); -
- dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。所以下标非0的元素都是应该是最大值。
- dp数组如何初始化
-
- 确定遍历顺序 求组合,不在乎顺序
遍历顺序为:coins(物品)放在外循环,target(背包)在内循环。且内循环正序。
- 确定遍历顺序 求组合,不在乎顺序
- 5.举例推导dp数组
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:dp = [amount+1] * (amount + 1)dp[0] = 0for coin in coins:for j in range(coin,amount+1):dp[j] = min(dp[j - coin] + 1 , dp[j])return dp[amount] if dp[amount] < amount + 1 else -1
279.完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
人话:完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
- 1.确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j] - 2.确定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]); - 3.dp数组如何初始化
dp[0]表示和为0的完全平方数的最小数量,那么dp[0]一定是0。
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。 - 4.确定遍历顺序
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
所以本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的! -
- 举例推导dp数组
class Solution:def numSquares(self, n: int) -> int:'''先遍历背包, 再遍历物品'''# 初始化nums = [i**2 for i in range(1, n + 1) if i**2 <= n]dp = [10**4]*(n + 1)dp[0] = 0# 遍历背包for j in range(1, n + 1):# 遍历物品for num in nums:if j >= num:dp[j] = min(dp[j], dp[j - num] + 1)return dp[n]
相关文章:
 322. 零钱兑换 279.完全平方数)
代码随想录NO42 | 动态规划_Leetcode70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数
动态规划_Leetcode70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数70. 爬楼梯 (进阶) 在原题基础上,改为:一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶…...

【C++从入门到放弃】初识C++(基础知识入门详解)
🧑💻作者: 情话0.0 📝专栏:《C从入门到放弃》 👦个人简介:一名双非编程菜鸟,在这里分享自己的编程学习笔记,欢迎大家的指正与点赞,谢谢! C基础…...

企业工程项目管理系统源码+spring cloud 系统管理+java 系统设置+二次开发
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...
【GPLT 三阶题目集】L3-016 二叉搜索树的结构
二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、右子树也分…...

核心交换机安全多业务高性能万兆交换机
RG-S5750-24SFP/12GT交换机是锐捷网络推出的融合了高性能、高安全、多业务的新一代三层交换机。RG-S5750-24SFP/12GT 交换机能够提供灵活的介质接口,满足网络建设中不同介质的连接需要。全千兆的端口形态,加上可扩展的高密度万兆端口,提供1&a…...
【静默安装的实现方案】)
Android APK 签名打包原理分析(三)【静默安装的实现方案】
背景 小编目前从事的系统定制类工作,有客户提出了,需要后台“静默安装”他们的app,也就是悄无声息的安装,而且特别强调,不可以跳出任何安装引导页面,他们的app下载完成之后,后台调用公开的android install代码,系统就后台完成安装,安装完成之后,重新打开应用就可以。…...

mulesoft MCIA 破釜沉舟备考 2023.02.14.05
mulesoft MCIA 破釜沉舟备考 2023.02.14.05 1. Refer to the exhibit.2. A Kubernetes controller automatically adds another pod replica to the resource pool in response to increased application load.3. An XA transaction Is being configured that involves a JMS c…...
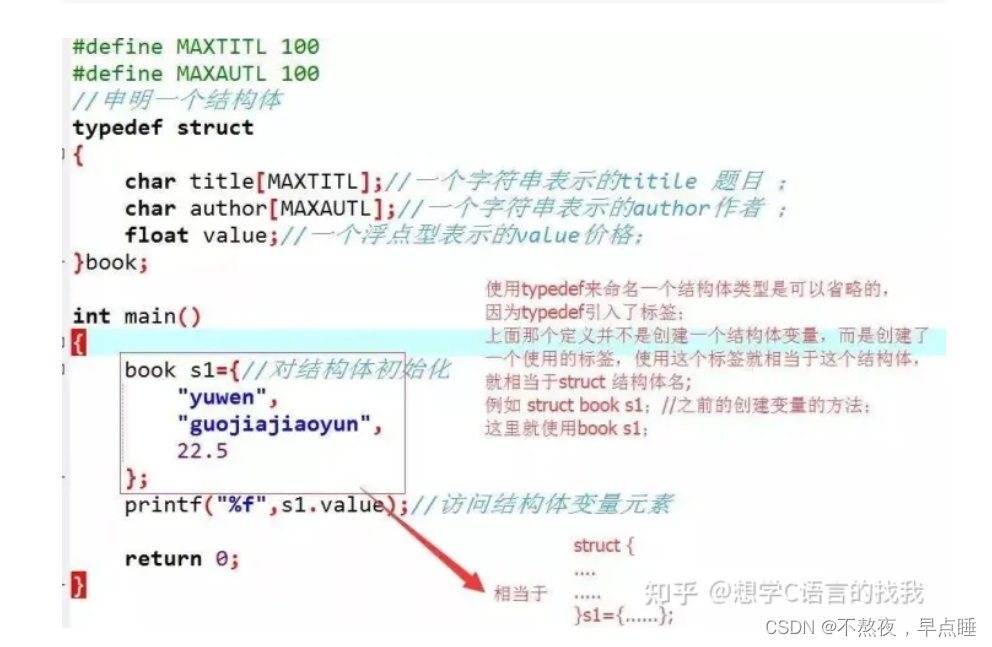
结构体的三种定义方法、结构体类型名(可选标志符)什么时候可以省略
结构体的三种定义方法 一、单独定义: 先定义结构体类型,再定义变量 定义结构体的格式如下: struct 结构体名 { 若干数据项; } ; 其中,struct为关键字; 结构体名是用户定…...

cgo静态编译不能用glibc,用musl
Golang 的一个动态链接依赖问题 upx 是一个压缩二进制的工具,如上图,经过压缩之后,这些 binary 的体积都减少了 46%。 静态链接 CGO 的依赖 如果使用 glibc 的是,是不能静态链接的: rootf88271a666f9:/workspace# g…...

力扣解法汇总1124. 表现良好的最长时间段
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。…...
12- 降维算法 (PCA降维/LDA分类/NMF) (数据处理)
数据降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。PCA算法有两种实现方法: 基于特征值分解协方差矩阵实现PCA算法基于SVD分解协方差矩阵实…...

QT+ OpenGL学习
文章目录QT OpenGLQOpenGLWidget:不需要GLFWQOpenGLFunction_X_X_Core:不需要GLAD你好,三角形顶点输入顶点着色器片段着色器链接着色器本节代码元素缓冲对象EBOQT交互GLSLGLSL支持的类型输入输出Uniform纹理纹理单元纹理环绕纹理过滤多级渐远纹理QT OpenGL 本篇完整…...

C语言(字符串输入)
目录 一.gets和puts组合 二.fgets()和fputs() 三.fgets()函数返回 四.fgets读取满问题 五.修改fgets函数,自动用\0替换\n 一.gets和puts组合 Gets()读取整行输入,知道遇到换行符,然后丢弃换行符,存储其余字符,并在这些字符的…...
(JAVA))
背包问题求方案数(AcWing)(JAVA)
有 N件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i 件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出 最优选法的方案数。注意答案可能很大,请输出答…...
一篇文章带你读懂HashMap
HashMap是面试中经常问到的一个知识点,也是判断一个候选人基础是否扎实的标准之一。可见HashMap的掌握是多重要。 一、HashMap源码分析 1、构造函数 让我们先从构造函数说起,HashMap有四个构造方法,别慌 1.1 HashMap() // 1.无参构造方法、// 构造一…...

Java如何进行优雅的判空——Optional类的灵活应用
0 引言 在Java Web项目开发中,经常令人头疼的NPE问题(NullPointerException)——空指针,例如我们在调用equal()方法时,就经常会出现NPE问题: String str null; str.equals("fsfs");…...

Fluent Python 笔记 第 12 章 继承的优缺点
重点是说明对 Python 而言尤为重要的两个细节: 子类化内置类型的缺点多重继承和方法解析顺序 12.1 子类化内置类型很麻烦 内置类型(使用 C 语言编写)不会调用用户定义的类覆盖的特殊方法。 不要子类化内置类型,用户自己定义的类应 该继承 collections 模块(http…...

Go语言读取解析yml文件,快速转换yml到go struct
YAML (YAML Aint a Markup Language)是一种标记语言,通常以.yml为后缀的文件,是一种直观的能够被计算机程序识别的数据序列化格式,并且容易被人类阅读,容易和脚本语言交互的,可以被支持YAML库的不同的编程语言程序导入…...
)
第二十六章 java并发常见知识内容(ThreadLocal 详解)
JAVA重要知识点带着疑问看ThreadLocalGC 之后 key 是否为 null?ThreadLocalMap Hash 算法ThreadLocalMap Hash 冲突ThreadLocalMap.set()方法ThreadLocalMap过期 key 的探测式清理流程ThreadLocalMap扩容机制ThreadLocalMap.get()详解ThreadLocalMap过期 key 的启发…...

人类的第一语言是什么
其实机器智能始终存在一个争议 没有人类的肢体和感受器无法理解和感同身受 这不用想是自然,但是可以通过虚拟数据进行模拟,深度学习便是 深度学习是模拟简单输入输出的最好选择,但不是开放性的学习 没有智能交互的智能永远不是智能 就像狼孩一…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
