MySQL索引数据结构入门
之前松哥写过一个 MySQL 系列,但是当时是基于 MySQL5.7 的,最近有空在看 MySQL8 的文档,发现和 MySQL5.7 相比还是有不少变化,同时 MySQL 又是小伙伴们在面试时一个非常重要的知识点,因此松哥打算最近再抽空和小伙伴们聊一聊 MySQL,讲讲原理,讲讲优化,我会从最基本最简单的开始,和大家梳理 MySQL 中常见的面试知识点。
本文我们就先从最简单的索引开始吧~
1. 什么是索引
说到索引,最常见的例子就是查字典,当我们需要查询某一个字的含义时,正常操作都是先根据字典的索引,找到该字在哪一页,然后直接翻到该页就行了。如果没有这个索引的话,那么我们就得一页一页的翻字典,直到找到该字。很明显,相对于第一种方案,第二种方案效率就要低很多了。
数据库中的索引也是类似的。
索引,我们也称之为 index 或者 key,当数据量比较少的时候,索引对于查询产生的效果并不明显,所以索引常常被人所忽略,但是当数据量比较大的时候,一个优秀的索引对查询产生的影响就是非常明显的了。在我们所掌握的各种 SQL 优化策略中,索引对 SQL 优化产生的效果算是最好的了,用好索引,SQL 性能可能会提升好几个数量级。
这里有的小伙伴可能会有一个疑惑,很多索引优化策略都是针对传统的机械硬盘的,然而现在我们大部分都是固态硬盘(SSD),很多针对机械硬盘的优化策略在 SSD 上似乎并没有必要,那还有必要去考虑索引优化吗?答案当然是有!无论是用什么样的磁盘,索引优化的整体原则都是不变的,只不过在 SSD 上,如果你的索引没有创建好,那么它对查询的影响不像对机械硬盘那么糟糕。
2. 索引的数据结构
2.1 B+Tree 和 B-Tree
小伙伴们知道,由于 MySQL 中的存储引擎设计成了可插拔的形式,任何机构和个人如果你有能力,都可以设计自己的存储引擎,而 MySQL 的索引是在存储引擎层实现的,而不是在服务器层实现的,所以不同存储引擎的索引工作方式都不一样,甚至,相同类型的索引,在不同的存储引擎中实现方案都不同。
本文松哥主要和小伙伴们介绍我们日常开发中最最常见的 InnoDB 存储引擎中的索引。
小伙伴们知道,InnoDB 存储引擎的索引数据结构是一个 B+Tree,至于什么是 B+Tree,这并非本文的重点,我这里不啰嗦,不了解 B+Tree 的小伙伴可以自行搜索一下学习一下。
假设我有如下数据:
| username | age | address | gender |
|---|---|---|---|
| ab | 99 | 深圳 | 男 |
| ac | 98 | 广州 | 男 |
| af | 88 | 北京 | 女 |
| bc | 80 | 上海 | 女 |
| bg | 85 | 重庆 | 女 |
| bw | 95 | 天津 | 男 |
| bw | 99 | 海口 | 女 |
| cc | 92 | 武汉 | 男 |
| ck | 90 | 深圳 | 男 |
| cx | 93 | 深圳 | 男 |
现在我给 username 和 age 字段建立联合索引,那么最终数据在磁盘上的存储结构是 B+Tree,为了小伙伴能够更好的理解 B+Tree 和 B-Tree,我画了如下两张图:


这两张图看懂了,InnoDB 存储引擎的索引我觉得基本上都搞懂了 80% 了,松哥来和大家稍微梳理一下这张图:
-
首先这两张图都是一个多路平衡查找树,即,不是二叉树,是多叉树。
-
绿色的方块表示指向下一个节点的指针;红色的方块表示指向下一个叶子节点的指针(B-Tree 中不存在该部分);带阴影的矩形则表示索引数据。
-
B+Tree 非叶子节点只保存关键字的索引和指向下一个节点的指针(绿色区域),所有的数据最终都会保存到叶子节点。因此在具体的搜索过程中,所有数据都必须要到叶子节点才能获取到,因此每次数据查询所需的 IO 次数都一样,这也就意味着 B+Tree 的查询速度比较稳定。
如果是 B-Tree 则分支节点上也保存了指向具体数据的指针,并且分支节点上出现的索引数据不会再次出现在叶子节点中,所以搜索的时候可能搜索到分支节点就找到需要的数据了,搜索效率不稳定,如 af 在分支节点上就找到了,而 ac 则要到叶子节点上才能找到)。
-
B+Tree 中,由于分支节点只保存索引数据和指向下一个节点的指针,所以在相同的磁盘空间中,能够指向更多的子节点,这就意味树的高度更低,搜索所需要的 IO 次数更少,搜索效率更高。
B-Tree 中,由于分支节点不仅保存索引数据和指向下一个节点的指针,还保存了指向具体数据的指针,所以在相同的空间下能够指向的子节点数量就少于 B+Tree,这就意味着相同的数据量,B-Tree 树高更高,搜索所需的 IO 次数更多,搜索效率低。
-
B+Tree 叶子节点的关键字从小到大按顺序排列,左边结尾数据都会保存右边节点开始数据的指针(红色区域),这个指针在范围搜索的时候非常有用,例如想搜索姓名在 ac~bc 之间的数据,按照树找到第一个节点 ac 之后,顺着指针一直往后找,找到第一个不满足条件的数据结束。
如果是 B-Tree 则没有 ac 指向 bc 的指针,需要先回到分支节点 af 再继续向下搜索,效率就会低很多。
-
B+Tree 的叶子节点都是有序排列的,所以 B+Tree 对于数据的排序有着更好的支持。
B-Tree 由于有一部分数据保存在分支节点中,叶子节点并不是完整的数据,所以对于排序、范围搜索的支持并不如 B+Tree。
-
B+Tree 数据划分的原则是左闭右开,以 (af,88) 这个节点为例,小于 (af,88) 节点的在左边,大于等于 (af,88) 节点的在右边。
B-Tree 则是左开右开。
-
B+Tree 全表扫描更快,因为所有数据都出现在叶子节点上,并且叶子节点之间还有指针相连,直接遍历即可。
B-Tree 在全表扫描的时候则需要对树的每一层进行遍历才能读到所有数据。
-
叶子节点指向数据的指针,如果是聚簇索引,则指向的是表中一条完整的记录;如果是非聚簇索引,则指向的是具体的主键值。在以非聚簇索引为依据进行搜索的时候,先找到记录的主键值,再根据 主键值去聚簇索引找到完整的记录,这个过程就是回表(InnoDB 中)。
好了,相信通过上面八点的介绍,大家对于 B-Tree 和 B+Tree 已经有了基本的认知了。
当我们想要搜索一条记录的时候,顺着根节点从上往下扫描树,比直接遍历一条一条的记录显然是要快很多。
说一个不太恰当的比喻,MySQL 中的数据存储,就像是通过一个链表把所有数据按照顺序串到一起,然后在这个链表上面又架了一个多路平衡查找树的感觉,搜索的时候,按照链表一个一个找,就是全表扫描;从树的根节点开始找,就是用索引。
2.2 树高问题
一个经典的问题,高度为 3 的 B+Tree 大概可以保存多少条数据?
计算机在存储数据的时候,最小存储单元是扇区,一个扇区的大小是 512 字节,而文件系统(例如 XFS/EXT4)最小单元是块,一个块的大小是 4KB。但是 InnoDB 在进行磁盘操作的时候,并不是以扇区或者块为依据的,InnoDB 在进行磁盘操作的时候,是以页为单位的,有时候也称作逻辑页,每个逻辑页的大小默认是 16KB,即四个块。这就意味着,InnoDB 在实际操作磁盘的时候,每次从磁盘上读取数据,至少读取 16KB,每次向磁盘上写数据,也至少写 16KB,并不是你需要 1KB 就读取 1KB,即使你只需要 1KB 的数据,InnoDB 也会从磁盘中将 16KB 的数据读取到内存中。
通过如下命令我们可以查看 MySQL 中 InnoDB 存储引擎逻辑页的大小:

16384/16=1024
前面的结论没问题。
以聚簇索引为例,现在我们假设数据库中一条记录的大小是 1KB,那么一个逻辑页就可以存 16 条数据(叶子节点)。
对于非叶子节点存储的则是主键值+指针,在 InnoDB 中,一个指针的大小是 6 个字节,假设我们的主键是 bigint ,那么主键占 8 个字节,当然还有其他一些头信息也会占用字节我们这里就不考虑了,我们大概算一下,小伙伴们心里有数即可:
16*1024/(8+6)=1170
即一个非叶子节点可以指向 1170 个子节点,那么一个三层的 B+Tree 可以存储的数据量为:
1170*1170*16=21902400
可以存储 2100万 条数据。
在 InnoDB 存储引擎中,B+Tree 的高度一般为 2-4 层,这就可以满足千万级的数据的存储,查找数据的时候,一次页的查找代表一次 IO,那我们通过主键索引查询的时候,其实最多只需要 2-4 次 IO 操作就可以了。
2.3 什么样的搜索可以用到索引?
根据前面的介绍,我们可以得出结论,在以下类型的搜索中,会用到索引:
- 全值匹配
如上图中,如果我们要搜索 username 为 ac 且 age 为 98 的用户,就可以直接使用索引精确定位到。
- 最左匹配
如果我们只是想搜索 username 为 ac 的用户,很明显也可以使用上图索引,因为用户名是有序的。在上图中,username 和 age 组成了联合索引,其中 username 在前,age 在后,所以索引是先按照 username 进行排序,username 相同的时候,再按照 age 进行排序的(如 bw 这个用户),如果我们按照 username 进行搜索,那么没问题,可以用上索引;但是如果我们按照 age 进行搜索,很明显,age 在整个索引树中是无序的,所以当我们使用 age 作为搜索条件的时候,是没法使用上图这个联合索引的。
- 前缀匹配
如果我们搜索的关键字只是 username 字段的前半部分,那么很明显,也是可以使用索引的,例如搜索所有以 a 开始的 username。
- 范围匹配
如果我们的搜索条件是一个范围,很明显也可以使用到上述索引,例如搜索姓名介于 ab~cc 之间的用户,只需要先从索引树的根节点开始,先找到 ab,然后根据叶子节点之间的指针顺藤摸瓜,找到 cc 之后的第一个数据(不满足条件的第一个数据)结束。
- 前面全值匹配,后面范围匹配
例如查找 username 为 bw 且 age 介于 90~99 之间的用户,这种情况也可以使用到上图的索引。在上图索引树中,当 username 相同的时候,就是按照 age 排序的,所以对于 username 都为 bw 的用户,它就是按照 age 进行排序的,此时,我们当然可以按照 age 的范围进行搜索了。
- 覆盖索引
有的时候,我们搜索的数据都在索引树中了,例如上图中的索引,我们想搜索 username 为 bw 的用户的 age,由于 age 就在索引树中,直接返回即可,这就是覆盖索引了。
2.4 使用限制
毫无疑问,基于 B+Tree 的索引,其实也存在一些使用限制。例如:
- 如果我们将 age 作为搜索条件,虽然 age 也是联合索引的一部分,但是 age 整体上在索引树中是无序的,所以将 age 作为搜索条件是没法使用上述索引的。
- 基于第一点,如果联合索引中还有第三、第四列等,那么凡是跳过第一列直接使用后面的列作为查询条件,索引都是不会生效的。
- 范围条件的右边无法使用索引直接定位。例如搜索 username 以 a 开头并且年龄为 99 的用户:
where username like 'a%' and age=99,此时 age=99 这个条件就无法在索引树中直接处理了(可以通过索引下推过滤)。原因很简单,当我们找到所有 username 以 a 开始的用户之后,这些用户的 age 并不是有序的,所以 age 就没法继续使用索引搜索了(但是可以通过索引下推过滤)。
关于第三点,我举一个例子,假设我们还有两个用户,分别是:
- username 为 ad 且 age 为 80;
- username 为 ae 且 age 为 88;
那么我们完善一下上面 B+Tree 的图应该变成下面这样:

可以看到,username 以 a 开始的用户,age 并不是有序的,所以就只能通过索引下推过滤了,而无法直接通过索引扫描定位数据。
对于第三点,如果范围搜索的字段值的可能性比较少,则可以通过多个等于比较来代替范围搜索。
2.5 自适应哈希索引
Hash 索引在 MySQL 中主要是 Memory 和 NDB 引擎支持,InnoDB 索引本身是 不支持的,但是 InnoDB 索引有一个特性叫做自适应哈希索引,自适应三个字意味着整个过程是全自动的,不需要开发者配置。
当 InnoDB 监控到某些索引值被频繁的访问时,那么它就会在 B+Tree 索引之上,构建一个 Hash 索引,进而通过 Hash 查找来快速访问数据。
默认情况下,自适应哈希索引是开启的状态,通过如下 SQL 我们可以查看:
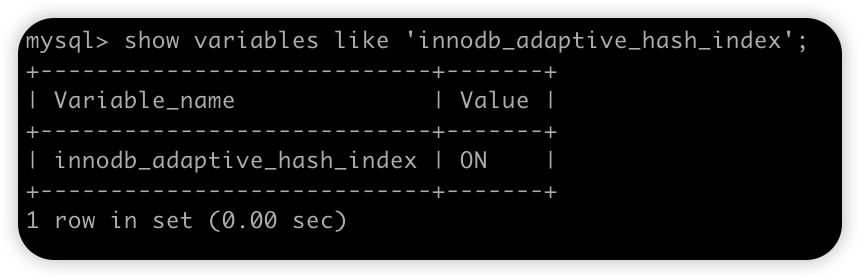
可以看到,这个默认就是开启的。
3. 小结
整体上来说,使用索引有如下优点:
- 减少了服务器需要扫描的数据量。
- 索引可以帮助服务器避免排序和创建临时表。
- 索引将随机 IO 变为了顺序 IO。
相关文章:

MySQL索引数据结构入门
之前松哥写过一个 MySQL 系列,但是当时是基于 MySQL5.7 的,最近有空在看 MySQL8 的文档,发现和 MySQL5.7 相比还是有不少变化,同时 MySQL 又是小伙伴们在面试时一个非常重要的知识点,因此松哥打算最近再抽空和小伙伴们…...
)
《低代码PaaS驱动集团企业数字化创新白皮书》-低代码PaaS应对行业集团企业数字化应用的需求(制造)
低代码PaaS应对行业集团企业数字化应用的需求 制造 制造业是我国重要的经济支柱之一,随着经济结构的调整,产业链的转移,劳动密集型制造业的利润已大不如前。在数字经济的大环境下,诸多制造业企业选择数字化转型,通过…...
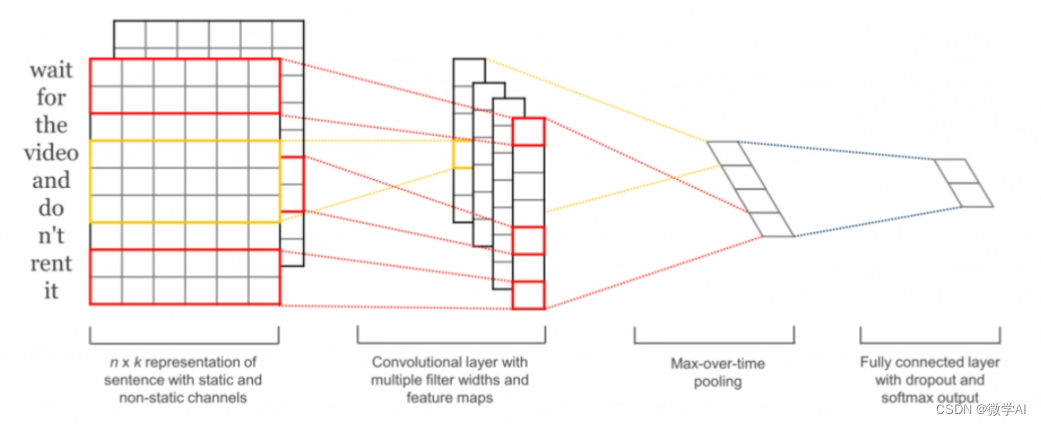
深度学习实战26-(Pytorch)搭建TextCNN实现多标签文本分类的任务
大家好,我是微学AI,今天给大家介绍一下深度学习实战26-(Pytorch)搭建TextCNN实现多标签文本分类的任务,TextCNN是一种用于文本分类的深度学习模型,它基于卷积神经网络(Convolutional Neural Networks, CNN)实现。TextCNN的主要思想…...
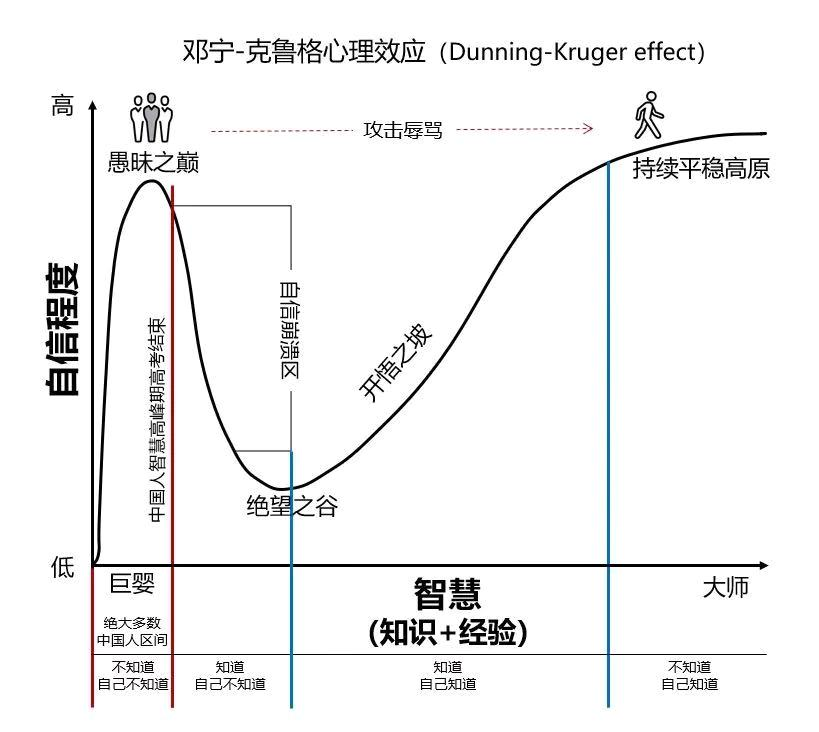
还在精神内耗?还在焦虑?可以看看这个
作为一个即将毕业的本科生,总是会不由自主的焦虑。因为不考研,所以显得和同学们格格不入,每天都在进行精神内耗,但是我不经意间看到了一个东西-《邓宁克鲁格效应》 上述的四个阶段刻画出了一条典型的“大师养成之路”。但大师毕竟…...
)
Event Camera (事件相机)
1.传统相机的缺点 1.随着计算机视觉领域的不断发展,目标检测的算法也越来越多样化,特别是近些年深度学习在计算机视觉领域的进步,已经产生了很多优秀的目标检测方法,这些基于帧的方法对于图片的质量有一定的要求,比如合…...

藏经阁(七)有源蜂鸣器和无源蜂鸣器 解析
文章目录 特征区别场景选型实战应用 特征 有源蜂鸣器特征: 又被称为直流蜂鸣器包含了一个多谐振荡器只要额定直流电压可以在两端发出声音具有驱动控制简单价格略高 无源蜂鸣器特征: 又被称为交流蜂鸣器内部没有振荡器需要在两端施加特定频率的方波电…...
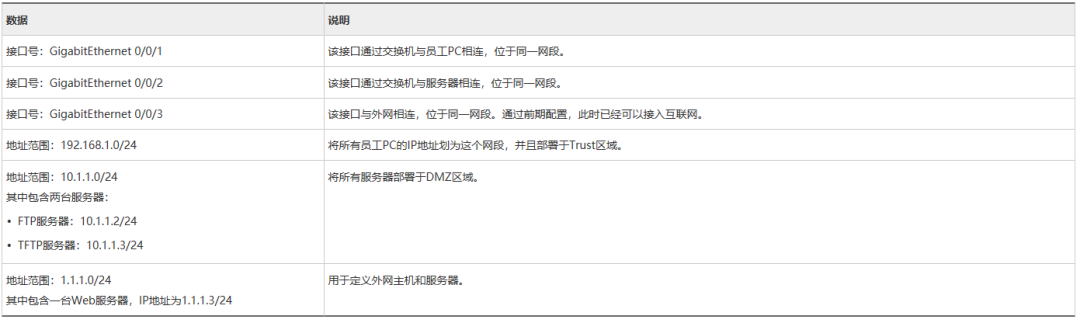
配置FTP/TFTP协议的ASPF
在多通道协议和NAT的应用中,ASPF是重要的辅助功能。通过配置ASPF功能,实现内网正常对外提供FTP和TFTP服务,同时还可避免内网用户在访问外网Web服务器时下载危险控件。 组网需求 如图1所示,FW部署在某公司的出口,公司提…...

泛型基本说明
使用传统方法的问题分析 不能对加入到集合ArrayList中的数据类型进行约束(不安全)遍历的时候,需要进行类型转换,如果集合中的数据量较大,对效率有影响。泛型的好处 编译时,检查添加元素的类型,提…...

干洗店洗鞋下店预约小程序开发多少钱
干洗店小程序是一种便捷的移动应用程序,能够帮助用户快捷、轻松地处理干洗、洗衣和清洗等服务。随着智能手机普及和人们生活节奏的不断加快,越来越多人选择使用干洗店小程序来满足自己的日常衣物清洗需求。那干洗店小程序怎么弄,洗衣预约小程…...

用Python实现批量翻译文档文件
文件名批量翻译需要用到编程语言和相应的翻译 API,下面以 Python 和 Google 翻译 API 为例,介绍具体的实现步骤: 安装必要的 Python 库 使用 Python 代码进行文件名翻译需要先安装两个库:googletrans 和 os。 pip install goog…...
机器视觉公司,在玩一局玩不起的游戏
导语 有个著名咨询公司曾经预测过:未来只有两种公司,是人工智能的和不赚钱的。 它可能没想到,还有第三种——不赚钱的AI公司。 去年我们报道过“正在消失的机器视觉公司”,昔日的“AI 四小龙”( 商汤、旷视、云从、依图…...

Zephyr 消息队列
文章目录 简介数据结构k_msgq 定义消息队列发送消息k_msgq_put 接收消息k_msgq_get wait_q 的双重身份清理消息队列k_msgq_cleanup 重置消息队列k_msgq_purge 读取数据k_msgq_peekk_msgq_peek_at 缓冲区容量k_msgq_num_free_getk_msgq_num_used_get 简介 message queue 用于中…...

Jenkins自动化部署实例讲解
文章目录 前言实例讲解基本环境全局工具配置创建任务任务配置源码管理构建步骤(Build Steps)第一步:调用Maven第二步:执行shell启动容器 后记 前言 你平常在做自己的项目时,是否有过部署项目太麻烦的想法?…...

RK356X 解除UVC摄像头预览分辨率1080P限制
平台 RK3566 Android 11 概述 UVC: USB video class(又称为USB video device class or UVC)就是USB device class视频产品在不需要安装任何的驱动程序下即插即用,包括摄像头、数字摄影机、模拟视频转换器、电视卡及静态视频相机…...

English Learning - L2-14 英音地道语音语调 重音技巧 2023.04.10 周一
English Learning - L2-14 英音地道语音语调 重音技巧 2023.04.10 周一 课前热身重音日常表达节奏单词全部重读的句子间隔时间非重读单词代词和缩约词助动词声临其境语调预习 课前热身 学习目标 重音 重弱突出,重音突出核心表达的意思 重音是落在重读单词上&…...

3.6 n维随机变量
学习目标: 学习n维随机变量需要掌握一定的数学知识,包括多元微积分、线性代数和概率论等。要学习n维随机变量,我会采取以下步骤: 复习相关的数学知识:首先,我会复习多元微积分、线性代数和概率论的基本知…...
JavaSE学习进阶day06_02 Set集合和Set接口
第二章 Set系列集合和Set接口 Set集合概述:前面学习了Collection集合下的List集合,现在继续学习它的另一个分支,Set集合。 set系列集合的特点: Set接口: java.util.Set接口和java.util.List接口一样,同样…...
基于matlab分析卫星星座对通信链路的干扰
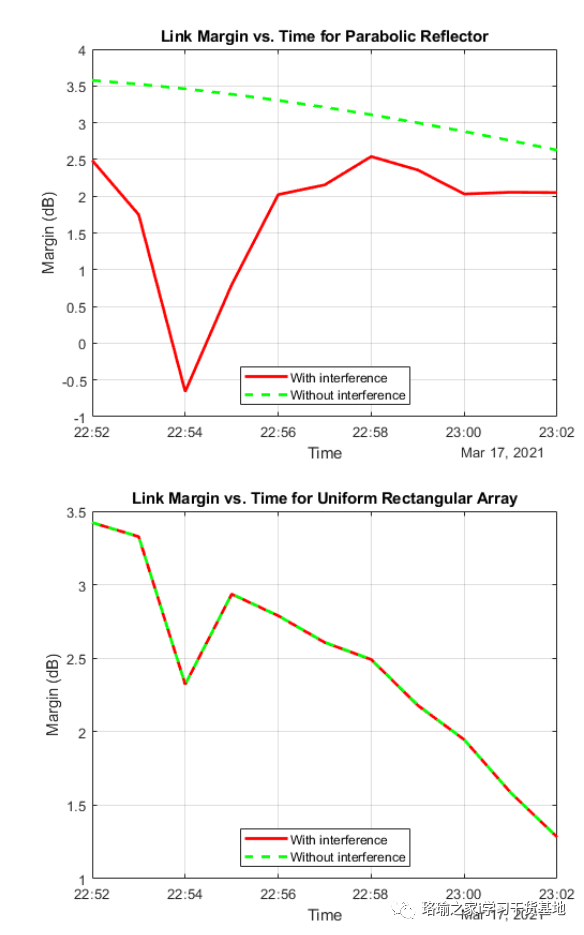
一、前言 此示例说明如何分析从中地球轨道 (MEO) 中的卫星星座到位于太平洋的地面站的下行链路上的干扰。干扰星座由低地球轨道(LEO)的40颗卫星组成。此示例确定下行链路闭合的时间、载波噪声加干扰比以及链路裕量。 此示例需要卫…...

Python中的异常——概述和基本语法
Python中的异常——概述和基本语法 摘要:Python中的异常是指在程序运行时发生的错误情况,包括但不限于除数为0、访问未定义变量、数据类型错误等。异常处理机制是Python提供的一种解决这些错误的方法,我们可以使用try/except语句来捕获异常并…...
Tomcat 部署与优化
1. Tomcat概述 Tomcat是Java语言开发的,Tomcat服务器是一个免费的开放源代码的Web应用服务器,是Apache软件基金会的Jakarta项目中的一个核心项目,由Apache、Sun和其他一些公司及个人 共同开发而成。Tomcat属于轻量级应用服务器,在…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
