3.6 n维随机变量
学习目标:
学习n维随机变量需要掌握一定的数学知识,包括多元微积分、线性代数和概率论等。要学习n维随机变量,我会采取以下步骤:
-
复习相关的数学知识:首先,我会复习多元微积分、线性代数和概率论的基本知识,包括向量、矩阵、行列式、概率密度函数、期望、方差等。
-
学习随机变量的基本概念:我会学习随机变量的基本概念,包括随机变量的定义、概率密度函数、累积分布函数、期望、方差等。
-
掌握n维随机变量的概念:我会学习n维随机变量的概念,包括随机向量的定义、联合概率密度函数、边缘概率密度函数、条件概率密度函数、协方差、相关系数等。
-
学习n维随机变量的分布:我会学习n维随机变量的分布,包括多元正态分布、卡方分布、t分布、F分布等。
-
掌握n维随机变量的应用:最后,我会学习n维随机变量在实际问题中的应用,例如回归分析、假设检验、贝叶斯统计等。
学习n维随机变量需要耐心和持续的努力,需要反复练习和思考,我相信通过不断的学习和实践,一定可以掌握这一领域的知识。

我的理解:
我们可以将n维随机变量看作是由n个随机因素决定的结果,每个随机因素可以对应一个分量。例如,我们可以将一个三维空间中的点的坐标看作是一个3维随机变量,其中每个分量表示一个坐标轴的值,这些坐标轴的值是由某些随机因素决定的。
另一个例子是在机器学习中,我们可以将一组数据的特征值看作是一个n维随机变量,其中每个分量表示一个特征的值。我们可以通过研究这个随机变量的统计性质来建立机器学习模型,例如分类、聚类、回归等。
需要注意的是,n维随机变量的随机性质不仅取决于每个随机因素本身的概率分布,还取决于各个随机因素之间的相关性。因此,在研究n维随机变量时,需要考虑到各个分量之间的关系。
我的理解:
如果你指的是“n维随机变量的分布函数”,那么可以这样理解:
在概率论中,随机变量是指可能取多个值中的一个,并且这个取值是不确定的。一个随机变量的分布函数描述了这个随机变量取值的概率分布情况,即它取某个值的概率大小。
对于一个n维随机变量,它是由n个随机变量组成的向量,其中每个随机变量都有自己的取值范围和概率分布情况。因此,我们需要一个n维随机变量的分布函数来描述这个n维向量的概率分布情况。
具体来说,n维随机变量的分布函数描述了在每个坐标轴方向上小于等于对应值的概率,即给定一个n维向量 (x_1,x_2,...,x_n),它的分布函数 F_{X_1,X_2,...,X_n}(x_1,x_2,...,x_n)表示了这个向量在每个坐标轴方向上小于等于对应值的概率。例如,F_{X_1,X_2}(x_1,x_2) 表示了在 X_1 方向上小于等于 x_1,在 X_2方向上小于等于 x_2的概率。这个概率可以是离散的或连续的,具体取决于随机变量的类型。
通过分布函数,我们可以计算出一些概率或期望值等重要的统计量,例如,计算n维随机变量的联合概率密度函数、边缘概率密度函数、条件概率密度函数等。因此,n维随机变量的分布函数是概率论和统计学中非常重要的概念。

我的理解:
在数学和概率论中,连续型随机变量是指可能取无限多个不同值的随机变量,其取值在某个区间内的概率密度函数是连续的。如果一个随机变量的取值可以由n个实数来表示,那么它就是一个n维随机变量。例如,二维随机变量的取值可以用二元组(X,Y)来表示。
对于一个n维连续型随机变量,我们可以用一个n维空间中的概率密度函数来描述它的取值分布。这个概率密度函数可以看作是一个对整个n维空间的赋值,每个点的赋值表示了该点的取值概率密度。与一维连续型随机变量类似,对于n维连续型随机变量,我们也可以计算出它在一个区域内的取值概率,这个概率可以看作是概率密度函数在这个区域上的积分。在实际应用中,n维连续型随机变量常常用于描述多个随机事件的联合概率分布,例如在金融领域中,可以用一个二维随机变量来描述股票的收益率和波动率。


总结:
n维随机变量是概率论中一个重要的概念,理解和掌握它对于很多应用领域都非常关键。以下是n维随机变量的一些重点、难点和易错点:
重点:
- 概率密度函数:n维随机变量的概率密度函数描述了它在n维空间中的取值分布情况。
- 联合概率分布:n维随机变量的联合概率分布描述了它与其他随机变量的联合概率分布情况。
- 边缘分布:从联合分布中可以得到n维随机变量的边缘分布,描述了其中任意一维的概率分布情况。
- 条件概率分布:给定其他随机变量的取值,n维随机变量的条件概率分布描述了它的取值情况。
难点:
- 多重积分:在计算n维随机变量的概率和期望等相关概念时,需要进行多重积分,这对于一些复杂的概率密度函数来说是比较困难的。
- 理解n维空间:理解n维空间的概念并不是很容易,需要具备较强的几何直观和数学能力。
- 计算复杂度:n维随机变量的计算复杂度往往会随着n的增加而增加,因此对于高维数据的处理需要更加高效的算法和计算方法。
易错点:
- 误解概率密度函数:概率密度函数并不等同于概率,只有通过积分才能得到概率值。
- 未考虑变量间的关系:n维随机变量的不同维度之间可能存在相关性,需要在计算时考虑这种关系。
- 对n维空间的误解:在理解n维随机变量时,容易将其看作是多个一维随机变量的简单组合,而忽略了其在n维空间中的内在特性和关系。

相关文章:

3.6 n维随机变量
学习目标: 学习n维随机变量需要掌握一定的数学知识,包括多元微积分、线性代数和概率论等。要学习n维随机变量,我会采取以下步骤: 复习相关的数学知识:首先,我会复习多元微积分、线性代数和概率论的基本知…...
JavaSE学习进阶day06_02 Set集合和Set接口
第二章 Set系列集合和Set接口 Set集合概述:前面学习了Collection集合下的List集合,现在继续学习它的另一个分支,Set集合。 set系列集合的特点: Set接口: java.util.Set接口和java.util.List接口一样,同样…...
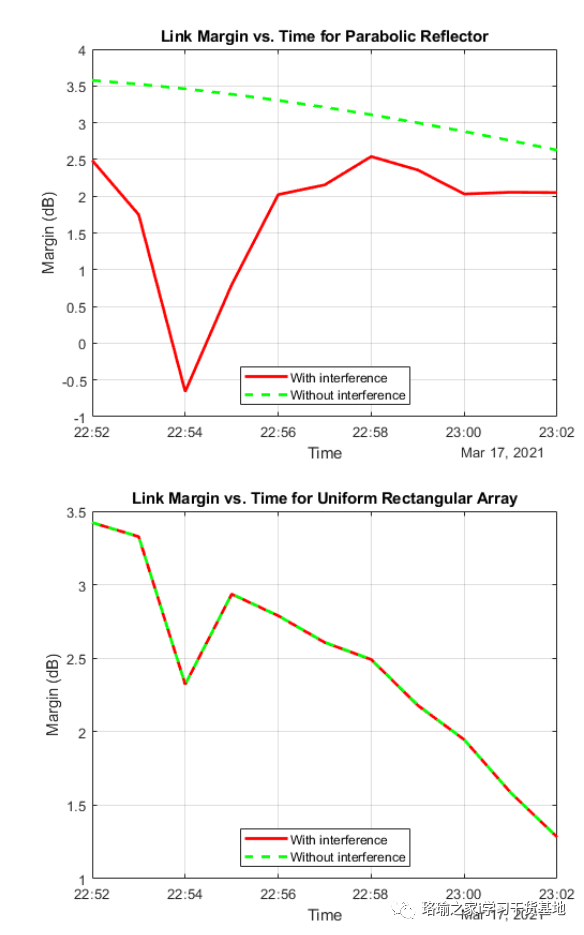
基于matlab分析卫星星座对通信链路的干扰
一、前言 此示例说明如何分析从中地球轨道 (MEO) 中的卫星星座到位于太平洋的地面站的下行链路上的干扰。干扰星座由低地球轨道(LEO)的40颗卫星组成。此示例确定下行链路闭合的时间、载波噪声加干扰比以及链路裕量。 此示例需要卫…...

Python中的异常——概述和基本语法
Python中的异常——概述和基本语法 摘要:Python中的异常是指在程序运行时发生的错误情况,包括但不限于除数为0、访问未定义变量、数据类型错误等。异常处理机制是Python提供的一种解决这些错误的方法,我们可以使用try/except语句来捕获异常并…...
Tomcat 部署与优化
1. Tomcat概述 Tomcat是Java语言开发的,Tomcat服务器是一个免费的开放源代码的Web应用服务器,是Apache软件基金会的Jakarta项目中的一个核心项目,由Apache、Sun和其他一些公司及个人 共同开发而成。Tomcat属于轻量级应用服务器,在…...

多模态之论文笔记ViLT
文章目录 ViLT: Vision-and-Language Transformer Without Convolution or Region Supervision一. 简介1.1 摘要1.2 文本编码器,图像编码器,特征交互复杂度分析1.2 特征交互方式分析1.3 图像特征提取分析 二. 方法 Vision-and-Language Transformer2.1.方…...
微服务架构下认证和鉴权理解
认证和鉴权 从单体应用到微服务架构,优势很多,但是并不是代表着就没有一点缺点了。 微服务架构,意味着每个服务都是松散耦合的。因此,作为软件工程师和架构师,我们在分布式架构中面临着安全挑战。微服务对外开放的端…...

Qt 网络编程之美:探索 URL、HTTP、服务发现与请求响应
Qt 网络编程之美:探索 URL、HTTP、服务发现与请求响应(The Beauty of Qt Network Programming: Exploring URL, HTTP, Service Discovery, and Request-Response 引言(Introduction)QUrl 类:构建和解析 URL(…...

毕业2年,跳槽到下一个公司就25K了,厉害了···
本人本科就读于某普通院校,毕业后通过同学的原因加入软件测试这个行业,角色也从测试小白到了目前的资深工程师,从功能测试转变为测试开发,并顺利拿下了某二线城市互联网企业的Offer,年薪 30W 。 选择和努力哪个重要&a…...

设计模式 -- 适配器模式
前言 月是一轮明镜,晶莹剔透,代表着一张白纸(啥也不懂) 央是一片海洋,海乃百川,代表着一块海绵(吸纳万物) 泽是一柄利剑,千锤百炼,代表着千百锤炼(输入输出) 月央泽,学习的一种过程,从白纸->吸收各种知识->不断输入输出变成自己的内容 希望大家一起坚持这个过程,也同…...
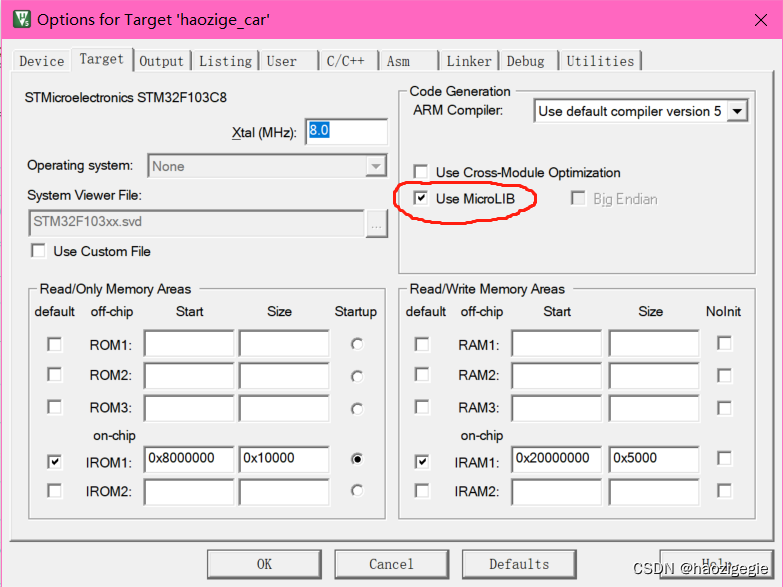
STM32之增量式编码器电机测速
STM32之增量式编码器电机测速 编码器编码器种类按监测原理分类光电编码器霍尔编码器 按输出信号分类增量式编码器绝对式编码器 编码器参数分辨率精度最大响应频率信号输出形式 编码器倍频 STM32的编码器模式编码器模式编码器的计数方向仅在TI1计数电机正转,向上计数…...

一图看懂 xlsxwriter 模块:用于创建 Excel .xlsx 文件, 资料整理+笔记(大全)
本文由 大侠(AhcaoZhu)原创,转载请声明。 链接: https://blog.csdn.net/Ahcao2008 一图看懂 xlsxwriter 模块:用于创建 Excel .xlsx 文件, 资料整理笔记(大全) 摘要模块图类关系图模块全展开【xlsxwriter】统计常量模块1 xlsxwrit…...

【社区图书馆】NVMe协议的命令
声明 主页:元存储的博客_CSDN博客 依公开知识及经验整理,如有误请留言。 个人辛苦整理,付费内容,禁止转载。 内容摘要 前言 命令由host提交到内存中的SQ队列中,更新TDBxSQ后,NVMe控制器通过DMA的方式将SQ中的命令(怎么取,如何取,取多少,因设计而异)取到控制器缓冲区…...

Nginx网站服务
Nginx概述 Nginx 是开源、高性能、高可靠、低资源消耗的 Web 和反向代理服务器,而且支持热部署,几乎可以做到 7 * 24 小时不间断运行,即使运行几个月也不需要重新启动,还能在不间断服务的情况下对软件版本进行热更新。对HTTP并发…...

第八篇 Spring 集成JdbcTemplate
《Spring》篇章整体栏目 ————————————————————————————— 【第一章】spring 概念与体系结构 【第二章】spring IoC 的工作原理 【第三章】spring IOC与Bean环境搭建与应用 【第四章】spring bean定义 【第五章】Spring 集合注入、作用域 【第六章】…...
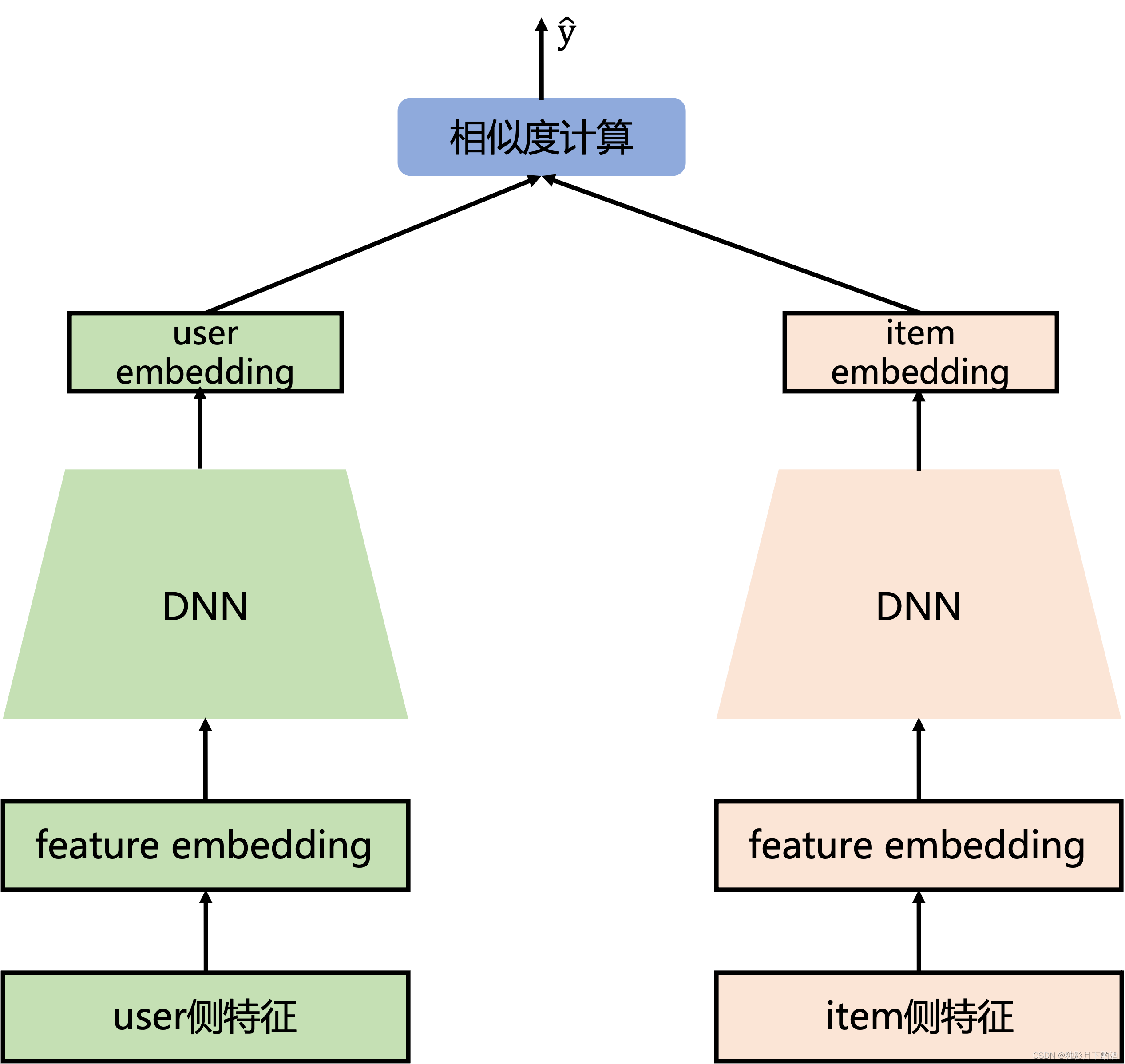
双塔模型:微软DSSM模型浅析
1.背景 DSSM是Deep Structured Semantic Model (深层结构语义模型) 的缩写,即我们通常说的基于深度网络的语义模型,其核心思想是将query和doc映射到到共同维度的语义空间中,通过最大化query和doc语义向量之间的余弦相似度,从而训…...

DAY 44 Apache网页优化
Apache网页优化 概述 在企业中,部署Apache后只采用默认的配置参数,会引发网站很多问题,换言之默认配置是针对以前较低的服务器配置的,以前的配置已经不适用当今互联网时代 为了适应企业需求,就需要考虑如何提升Apach…...

移动端手机网页适配iPad与折叠屏设备
采用的网页适配方案:移动端页面px布局适配方案(viewport) 产生此问题的原因 由于手机与平板等设备宽高比差异导致页面展示不全或者功能按钮展示在视口之外点击不到。 简单来说就是我们的页面都是瘦长(即高大于宽)的,而折叠屏等设…...

深入剖析 Qt QMap:原理、应用与技巧
目录标题 引言:QMap 的重要性与基本概念QMap 简介:基本使用方法(QMap Basics: Concepts and Usage)QMap 迭代器:遍历与操作键值对(QMap Iterators: Traversing and Manipulating Key-Value Pairs࿰…...

SpringBoot使用Hbase
SpringBoot使用Hbase 文章目录 SpringBoot使用Hbase一,引入依赖二,配置文件添加自己的属性三,配置类注入HBASE配置四,配置Hbase连接池五,配置操作服务类 一,引入依赖 <dependency><groupId>org…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

