15.2 矩阵链乘法
1.代码
public class MatrixChainMultiplication {public static void main(String[] args) {
// 在该代码中,我们首先创建了两个n * n的矩阵m和s,分别用于记录最优值和分割点。 其中m 矩阵 通过i j 来显示在i到j的矩阵链中最优解
//
// 然后,我们将i = j时的m[i][j]赋值为0,因为一个矩阵的乘积为0。
//
// 接下来,我们使用L循环枚举子问题规模,i循环枚举左端点,j循环枚举右端点,并使用k循环枚举分割点。
//
// 对于每个分割点k,我们计算最优值q,然后将q与m[i][j]进行比较,如果q小于m[i][j],则更新m[i][j]和s[i][j]。
// 通过公式算法导论15.7
//
// 最后,我们返回m[1][n-1],即原问题的最优值。
//
// 该算法的时间复杂度为O(n^3),其中n是矩阵的数量。int[] p = {30, 35, 15, 5, 10, 20, 25};System.out.println("最少的乘法次数为:" + matrixChainOrder(p));}
public static int matrixChainOrder(int[] p) {int n = p.length;// 创建n * n的矩阵m和s,用于记录最优值和分割点int[][] m = new int[n][n];int[][] s = new int[n][n];// i==j时,m[i][j]=0,因为一个矩阵的乘积为0for (int i = 1; i < n; i++) {m[i][i] = 0;}for (int i = 0; i < m.length; i++) {System.out.println(Arrays.toString(m[i]));}
// L是子问题规模for (int L = 2; L < n; L++) {// i是左端点,j是右端点,k是分割点for (int i = 1; i < n - L + 1; i++) {int j = i + L - 1;m[i][j] = Integer.MAX_VALUE;// 枚举分割点k,求解最优值for (int k = i; k < j; k++) {int q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];System.out.println("m[i][k]: "+m[i][k] );System.out.println("m[k + 1][j]: "+m[k + 1][j]);System.out.println("i:"+i+" k:"+k+" j:"+j);System.out.println(q);if (q < m[i][j]) {m[i][j] = q;s[i][j] = k;}}}}// 返回最优值return m[1][n - 1];}
}
2.原理
自己看算法导论吧
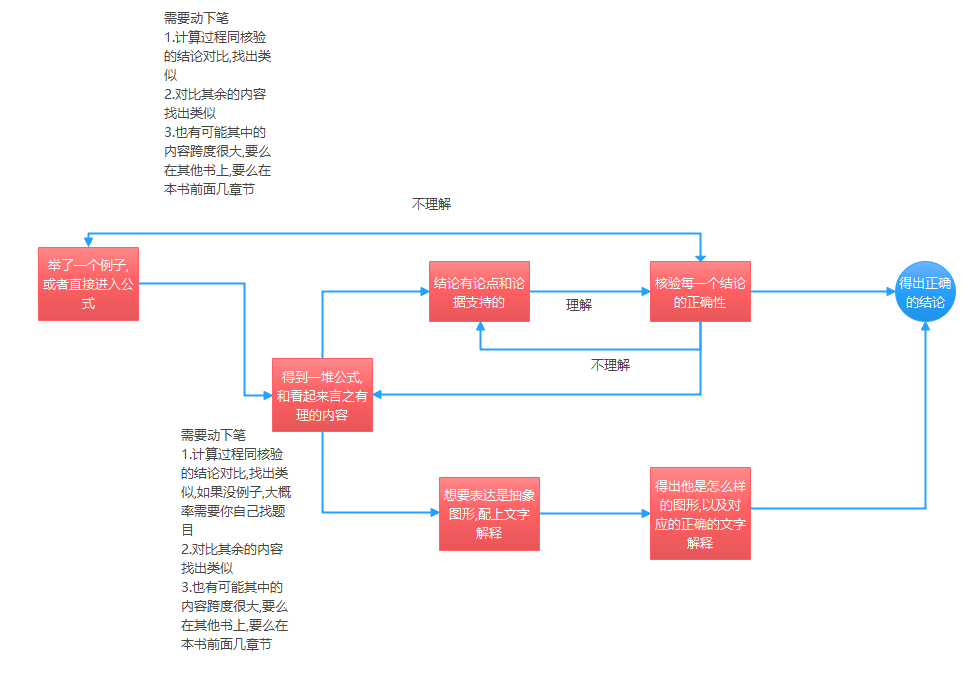
我再看到
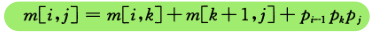
这条公式的时候很困惑,然后自己手算了他给的第一个例子才知道这是正确的.
3.问题
具体的问题已经在代码注释中讲解完毕
4.进阶
输出只是I一个普通的递归而已
package collection;
public class printOptimalParens {public static void matrixChainOrder(int[] p) {int n = p.length - 1;int[][] m = new int[n + 1][n + 1];int[][] s = new int[n + 1][n + 1];for (int i = 1; i <= n; i++) {m[i][i] = 0;}for (int len = 2; len <= n; len++) {for (int i = 1; i <= n - len + 1; i++) {int j = i + len - 1;m[i][j] = Integer.MAX_VALUE;for (int k = i; k <= j - 1; k++) {int q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];if (q < m[i][j]) {m[i][j] = q;s[i][j] = k;}}}}System.out.println("Optimal Parenthesization:");printOptimalParens(s, 1, n);}
public static void printOptimalParens(int[][] s, int i, int j) {if (i == j) {System.out.print("A" + i);} else {System.out.print("(");printOptimalParens(s, i, s[i][j]);printOptimalParens(s, s[i][j] + 1, j);System.out.print(")");}}
public static void main(String[] args) {int[] p = {30, 35, 15, 5, 10, 20, 25};matrixChainOrder(p);}
}
((A1(A2A3))((A4A5)A6))
相关文章:
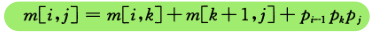
15.2 矩阵链乘法
1.代码 public class MatrixChainMultiplication {public static void main(String[] args) { // 在该代码中,我们首先创建了两个n * n的矩阵m和s,分别用于记录最优值和分割点。 其中m 矩阵 通过i j 来显示在i到j的矩阵链中最优解 // // …...
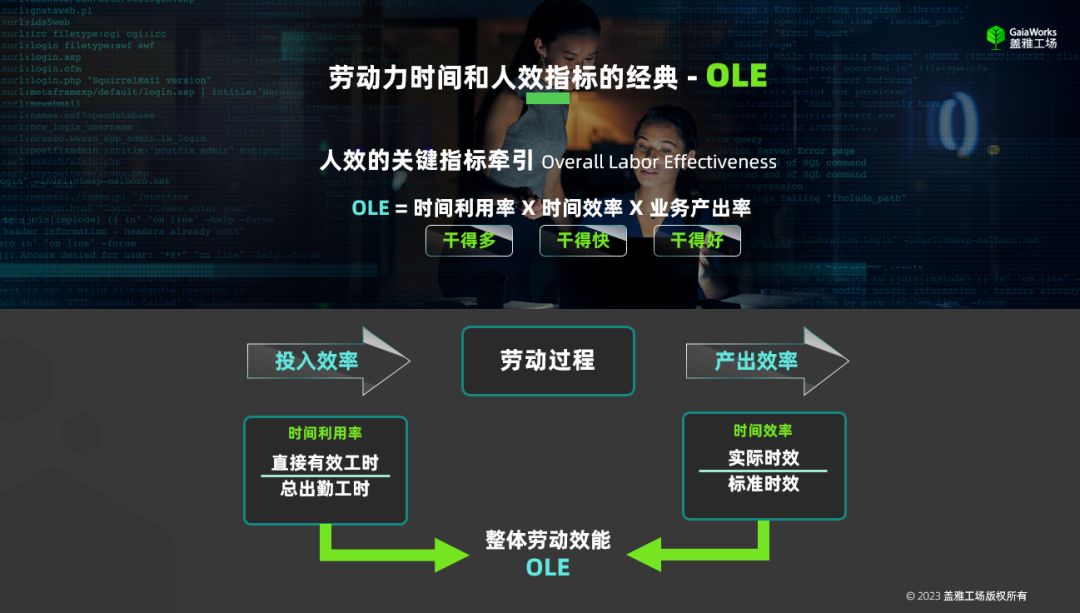
向隐形冠军学习:聚焦人效,用时间管理提效益
注: 本文来源于盖雅工场联合创始人兼CEO 章新波 在2023狮山论坛“ 向隐形冠军学习: 聚焦人效,用时间管理提效益 ”的主题分享。 文|章新波 整理 |盖雅学苑 在人力资源行业以及各大企业,「人效」这个词…...

Protocol Buffers Go Generated Code Guide
Protocol Buffers Go 代码生成指南 本主题准确描述了协议缓冲区编译器为任何给定的协议定义生成的Go代码。 编译器调用 协议缓冲区编译器需要一个插件来生成Go 代码。使用Go 1.16或更高版本安装,方法是运行: go install google.golang.org/protobuf/…...

Python VTK STL 映射三维模型表面距离
目录 前言: 效果: 实现步骤: Code: 前言: 本文介绍了Python VTK映射三维模型表面距离,通过如何使用VTK计算两个三维模型(stl)的表面距离,并将其距离值以颜色映射到模型,可用于对比 两相模型…...

C# 异常处理机制和常见的异常类型
在 C# 中,异常处理是一个非常重要的概念,它可以让我们在程序发生错误时进行有效的处理,使程序具备更好的鲁棒性。C# 异常处理机制基于 try-catch-finally 语句块,其基本用法如下: try {// 可能会抛出异常的代码 } cat…...

【0187】客户端身份验证配置文件视图之pg_hba_file_rules
文章目录 1. 客户端身份验证配置文件视图2. 视图效果相关阅读: 【0179】配置PostgreSQL以允许远程连接 【0180】PG内核通过pg_hba.conf完成客户端认证(1) 【0181】PG内核通过pg_hba.conf完成客户端认证(2)...
Python实现)
模糊层次分析法(FAHP)Python实现
文章目录 理论基础三角模糊数概念参考 Python源码测试 理论基础 \quad 模糊层次分析法( F A H P FAHP FAHP)将模糊理论( F u z z y S e t Fuzzy Set FuzzySet)嵌入到基本层次分析法( A H P AHP AHP)中。 A …...

gdb切换窗口焦点
为了辅助调试,一般会使用layout src,调起TUI显示代码: 然而这种情况下我们写命令很不方便,无法方便地使用上一条命令、退格等。 按动上下左右方向键盘只会移动代码框,然而在伪终端下,可以用鼠标滚轮来上下…...
【Spring Security】 入门实战
文章目录 一、基本概念二、Spring Security第一个程序三、Spring Security没有生效四、修改默认账号密码(appliction.yml)五、修改默认账号密码(配置类)六、Spring Security的三个configure方法七、Spring Security的三种身份的验…...
SpringBoot的Interceptor拦截器的简介和实际使用
拦截器(Interceptor) 概念:是一种动态拦截方法调用的机制,类似于过滤器。Spring框架中提供的,用来动态拦截控制器方法的执行。 作用:拦截请求,在指定的方法调用前后,根据业务需要执行…...

5个面向Python高级开发者的技巧
使用这些用于自定义类行为、编写并发代码、管理资源、存储和操作数据以及优化代码性能的高级技术来探索 Python 的深度。 本文探讨了 Python 中的五个高级主题,它们可以为解决问题和提高代码的可靠性和性能提供有价值的见解和技术。从允许您在定义类时自定义类行为的…...

Nginx简介
Nginx是什么?可以做什么事情? Nginx是高性能的HTTP和反向代理的web服务器,处理高并发的能力十分强大,能经受高负载的考研,有报告表明能能支持高达50000个并发连接数。 特点 占有内存少:一万个长连接&…...

十五分钟带你学会 Electron
文章目录 什么是 Electron为什么要选择 Electron安装 Electron桌面CSDN实战Electron 基础配置Electron 进程主进程渲染进程主进程与渲染进程的区别主进程与渲染进程的通信 Electron 跨平台问题Electron 部署打包应用程序发布应用程序 Electron 跨端原理总结 什么是 Electron E…...
设计模式-结构型模式之桥接模式
2. 桥接模式 2.1. 模式动机 设想如果要绘制矩形、圆形、椭圆、正方形,我们至少需要4个形状类,但是如果绘制的图形需要具有不同的颜色,如红色、绿色、蓝色等,此时至少有如下两种设计方案: 第一种设计方案是为每一种形状…...
软件测试工程师为什么要写测试用例?
软件测试工程师为什么要写测试用例?相信从事软件测试行业的从业者来讲,测试用例并不陌生。因为测试用例不仅仅是一组简单的文档,它包含前提条件、输入、执行条件和预期结果等等重要内容,并且能够完成一定的测试目的和需求。下面本…...

【DAY40】VUE练习
DOS命令: DOS(Disk Operating System)是一种操作系统,它使用命令行界面(Command Prompt)进行交互。在 DOS 中,有一些常用的命令,可以用来定位目录、创建、删除、拷贝文件和目录&…...

实模式的寄存器
实模式的寄存器有8个通用寄存器,分别为AX、BX、CX、DX、SI、DI、BP和SP。通用的意思就是它们之中的大部分可以根据需要用于多种目的。 AX: accumulator,累加寄存器 BX: base,基址寄存器 CX: count,计数寄存器 SI: Source Index&am…...
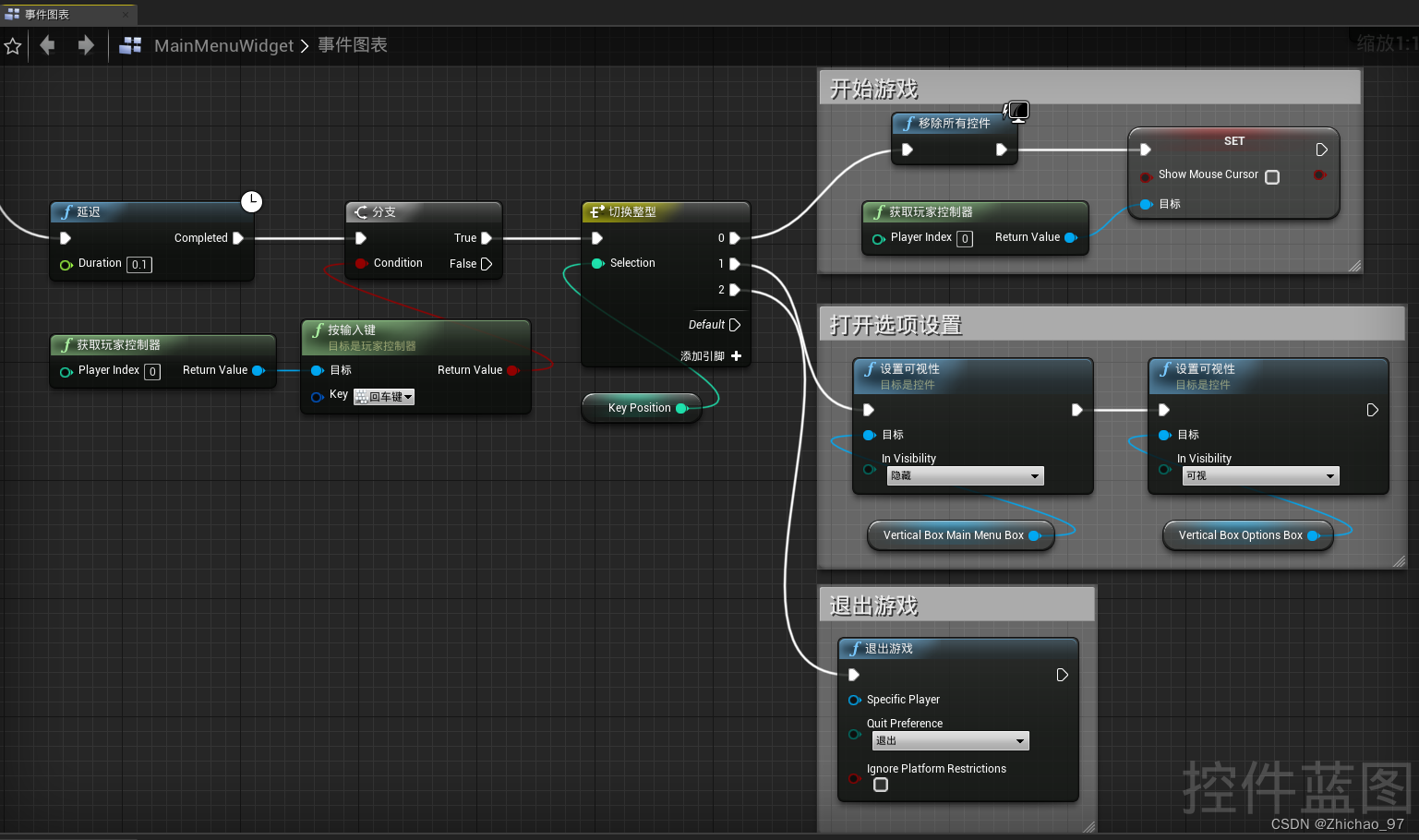
【UE 控件蓝图】通过键盘选中要点击的按钮 通过Enter键点击
上一篇【UE 控件蓝图】菜单及功能实现博客已经完成了菜单的制作,但是我们只能通过鼠标来点击菜单选项,本篇博客实现的是能够通过键盘的上下键来选中按钮,然后按下“Enter”键来实现点击按钮的效果。 效果 可以看到并没有移动鼠标也可以通过…...

SSR在天猫优品大促会场的探索实践
BBC 发现其网站加载时间每增加一秒,用户便会流失 10%。为提高页面的秒开率,我们不断探索着优化策略,仅仅在浏览器领域下的优化已经满足不了我们的极致要求,开始往服务端方向不断探索。本文将讨论业务接入SSR的几个问题:…...

WPF教程(一)---创建一个WPF程序基础知识
1.前言: 这篇主要讲WPF的开发基础,介绍了如何使用Visual Studio 2019创建一个WPF应用程序。 首先说一下学习WPF的基础知识: 1) 要会一门.NET所支持的编程语言--例如C#。 2) 会一点“标准通用标记语言”:WPF窗体程序使用的XAML语…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
