backward()和zero_grad()在PyTorch中代表什么意思
文章目录
- 问:`backward()`和`zero_grad()`是什么意思?
- backward()
- zero_grad()
- 问:求导和梯度什么关系
- 问:backward不是求导吗,和梯度有什么关系(哈哈哈哈)
- 问:你可以举一个简单的例子吗
- 问:上面代码中dw和db是怎么计算的,请给出具体的计算公式
问:backward()和zero_grad()是什么意思?
backward()和zero_grad()是PyTorch中用于自动求导和梯度清零的函数。
backward()
backward()函数是PyTorch中用于自动求导的函数。在神经网络中,我们通常定义一个损失函数,然后通过反向传播求出对于每个参数的梯度,用于更新模型参数。backward()函数会自动计算损失函数对于每个参数的梯度,并将梯度保存在相应的张量的.grad属性中。调用此函数时,必须先将损失张量通过backward()函数的参数gradient传递反向传播的梯度,通常为1。
import torch# 定义模型、损失函数和优化器
model = torch.nn.Linear(2, 1)
loss_fn = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)# 定义输入和目标输出
x = torch.tensor([[1., 2.], [3., 4.]])
y_true = torch.tensor([[3.], [7.]])# 前向传播
y_pred = model(x)
loss = loss_fn(y_pred, y_true)# 反向传播并更新参数
optimizer.zero_grad()
loss.backward()
optimizer.step()
在调用backward()函数时,gradient参数指定了反向传播的梯度。这个梯度是一个标量,表示损失函数对自身的导数,也就是说,它是一个常数。因此,通常将gradient参数设置为1,以表示损失函数对自身的导数为1。
在反向传播的过程中,每个参数的梯度都会乘以这个反向传播的梯度。因此,将gradient参数设置为1,可以使得每个参数的梯度都乘以1,即不改变原有的梯度值。
需要注意的是,如果损失函数不是标量,即它的输出是一个张量,那么在调用backward()函数时,gradient参数应该是一个和输出张量形状相同的张量,表示损失函数对输出张量的导数。在这种情况下,每个参数的梯度将会乘以对应的gradient张量的元素,而不是乘以一个标量。
zero_grad()
zero_grad()函数是PyTorch中用于梯度清零的函数。在每次更新参数之前,我们需要清零之前计算的梯度,否则会累加之前的梯度,导致参数更新不准确。zero_grad()函数会将所有参数的梯度清零,以便进行下一次前向传播和反向传播。
import torch# 定义模型、损失函数和优化器
model = torch.nn.Linear(2, 1)
loss_fn = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)# 定义输入和目标输出
x = torch.tensor([[1., 2.], [3., 4.]])
y_true = torch.tensor([[3.], [7.]])# 前向传播
y_pred = model(x)
loss = loss_fn(y_pred, y_true)# 反向传播并更新参数
optimizer.zero_grad()
loss.backward()
optimizer.step()# 再次进行前向传播和反向传播
x = torch.tensor([[5., 6.], [7., 8.]])
y_true = torch.tensor([[11.], [15.]])
y_pred = model(x)
loss = loss_fn(y_pred, y_true)
optimizer.zero_grad()
loss.backward()
optimizer.step()
问:求导和梯度什么关系
求导和梯度密切相关。在数学和机器学习中,梯度通常是一个向量,它由函数在不同自变量处的偏导数组成。因此,梯度向量是一个表示多元函数变化率的向量。
当我们需要求一个函数在某个点的梯度时,通常需要对函数在该点关于所有自变量的偏导数进行求导,因此求导和梯度密切相关。也就是说,梯度是由一组偏导数构成的向量,并且偏导数可以用求导来计算。
在机器学习中,梯度经常被用来对模型进行优化,特别是在梯度下降等优化算法中。在这些算法中,我们需要计算损失函数对模型参数的梯度,以便更新参数值从而最小化损失函数。因此,梯度是优化算法中非常重要的概念,而求导则是计算梯度的基础。
问:backward不是求导吗,和梯度有什么关系(哈哈哈哈)
backward()函数和梯度密切相关,因为在神经网络中,我们通常使用梯度下降等优化算法来更新模型的参数,而梯度是求导的结果。
在神经网络中,我们通常定义一个损失函数来衡量模型在训练集上的表现。然后,我们使用反向传播算法计算损失函数对于模型参数的梯度,即每个参数对于损失函数的偏导数。反向传播算法会遍历神经网络中的每一层,从输出层开始,计算对于每个参数的梯度。最后,我们使用这些梯度来更新模型的参数,以使损失函数最小化。
backward()函数在PyTorch中就是用来执行反向传播算法的。在执行backward()函数之前,我们需要调用loss.backward()将损失函数对于模型输出的梯度计算出来。然后,PyTorch会根据这个梯度,使用链式法则自动计算出每个参数的梯度,并将其保存在相应的张量的.grad属性中。
因此,backward()函数本质上就是求导的过程,它计算的是损失函数对于模型参数的梯度。这些梯度可以被用于更新模型参数,以最小化损失函数。
问:你可以举一个简单的例子吗
当我们训练一个简单的线性模型时,可以通过PyTorch的backward()函数和梯度下降算法来更新模型参数。
考虑如下的线性模型:
y = w ∗ x + b y=w*x+b y=w∗x+b
y = w * x + b
其中,y是模型的输出,也可以叫做 y p r e d y_{pred} ypred,也可以叫预测值,w是权重,b是偏置,x是输入。我们定义一个均方误差(MSE)损失函数:
l o s s = ( y t r u e − y p r e d ) 2 loss=(y_{true}-y_{pred})^2 loss=(ytrue−ypred)2
loss = (y_true - y)^2
其中,y_true是目标输出,是真实值,y是模型的输出,是预测值。 y t r u e − y y_{true} - y ytrue−y就是“真实值—预测值“。我们使用梯度下降算法来更新模型的权重和偏置。梯度下降算法的更新规则如下:
w = w − l r ∗ d w w=w-l_r*dw w=w−lr∗dw
b = b − l r ∗ d b b=b-l_r*db b=b−lr∗db
w = w - learning_rate * dw
b = b - learning_rate * db
其中,dw和db分别是权重和偏置的梯度,learning_rate是学习率,控制每次更新的步长。
现在,我们可以通过PyTorch的backward()函数来计算权重和偏置的梯度。假设我们有一个输入x和一个目标输出y_true,我们可以按照以下步骤训练模型:
import torch# 定义模型参数
w = torch.tensor([1.0], requires_grad=True)
b = torch.tensor([0.0], requires_grad=True)# 定义输入和目标输出
x = torch.tensor([2.0])
y_true = torch.tensor([4.0])# 定义损失函数
loss_fn = torch.nn.MSELoss()# 定义优化器
optimizer = torch.optim.SGD([w, b], lr=0.1)# 迭代训练
for i in range(100):# 前向传播y_pred = w * x + bloss = loss_fn(y_pred, y_true)# 反向传播optimizer.zero_grad()loss.backward()# 更新模型参数optimizer.step()# 输出模型参数
print("w = ", w)
print("b = ", b)
在上面的代码中,我们首先定义了模型的权重w和偏置b,并将它们设置为需要求导。然后,我们定义了输入x和目标输出y_true,以及损失函数和优化器。在每一轮迭代中,我们执行以下步骤:
- 前向传播:计算模型的输出
y_pred。 - 计算损失函数:使用损失函数计算预测输出
y_pred与目标输出y_true之间的均方误差。 - 反向传播:使用
loss.backward()计算损失函数对于权重w和偏置b的梯度。 - 更新模型参数:使用优化器的
step()函数根据梯度下降算法更新模型的权重和偏置。
在迭代完成后,我们输出模型的权重w和偏置b。这些参数已经被训练成使损失函数最小化的值。
问:上面代码中dw和db是怎么计算的,请给出具体的计算公式
在上面的代码中,dw和db分别是权重w和偏置b的梯度,可以通过PyTorch的自动求导机制自动计算得出。
具体来说,假设我们已经计算出了损失函数loss对于模型输出y_pred的梯度dy_pred,那么我们可以使用链式法则计算出损失函数对于权重w和偏置b的梯度dw和db:
d w = d l o s s d y _ p r e d ∗ d y _ p r e d d w = ( ( y t r u e − y p r e d ) 2 ) y _ p r e d ′ ∗ ( w ∗ x + b ) w ′ = 2 ( y _ p r e d − y _ t r u e ) ∗ x dw=\frac{dloss}{dy\_pred}*\frac{dy\_pred}{dw}=((y_{true}-y_{pred})^2)_{y\_{pred}}'*(w*x+b)_w'=2(y\_pred-y\_true)*x dw=dy_preddloss∗dwdy_pred=((ytrue−ypred)2)y_pred′∗(w∗x+b)w′=2(y_pred−y_true)∗x
d b = d l o s s d y _ p r e d ∗ d y _ p r e d d b = ( ( y t r u e − y p r e d ) 2 ) y _ p r e d ′ ∗ ( w ∗ x + b ) b ′ = 2 ( y _ p r e d − y _ t r u e ) db=\frac{dloss}{dy\_pred}*\frac{dy\_pred}{db}=((y_{true}-y_{pred})^2)_{y\_pred}'*(w*x+b)_b'=2(y\_pred-y\_true) db=dy_preddloss∗dbdy_pred=((ytrue−ypred)2)y_pred′∗(w∗x+b)b′=2(y_pred−y_true)
dw = dloss/dw = dloss/dy_pred * dy_pred/dw = 2(y_pred - y_true) * x
db = dloss/db = dloss/dy_pred * dy_pred/db = 2(y_pred - y_true)
其中,x是输入,y_pred是模型的输出。
在上面的代码中,我们使用loss.backward()计算损失函数对于模型参数的梯度,并将其保存在相应的张量的.grad属性中。具体来说,我们可以使用以下代码计算梯度:
# 反向传播
optimizer.zero_grad()
loss.backward()# 提取梯度
dw = w.grad
db = b.grad
在这里,我们首先使用optimizer.zero_grad()清除之前的梯度,然后使用loss.backward()计算损失函数对于模型参数的梯度。最后,我们可以使用w.grad和b.grad分别提取权重和偏置的梯度。
相关文章:
和zero_grad()在PyTorch中代表什么意思)
backward()和zero_grad()在PyTorch中代表什么意思
文章目录 问:backward()和zero_grad()是什么意思?backward()zero_grad() 问:求导和梯度什么关系问:backward不是求导吗,和梯度有什么关系(哈哈哈哈)问:你可以举一个简单的例子吗问&a…...
C++多线程编程(一) thread类初窥
多线程编程使我们的程序能够同时执行多项任务。 在C11以前,C没有标准的多线程库,只能使用C语言中的pthread,在C11之后,C标准库中增加了thread类用于多线程编程。thread类其实是对pthread的封装,不过更加好用ÿ…...

Qt QVector 详解:从底层原理到高级用法
目录标题 引言:QVector的重要性与简介QVector的常用接口QVector和std::Vector迭代器:遍历QVector 中的元素(Iterators: Traversing Elements in QVector)常规索引遍历基于范围的for循环(C11及以上)使用STL样…...
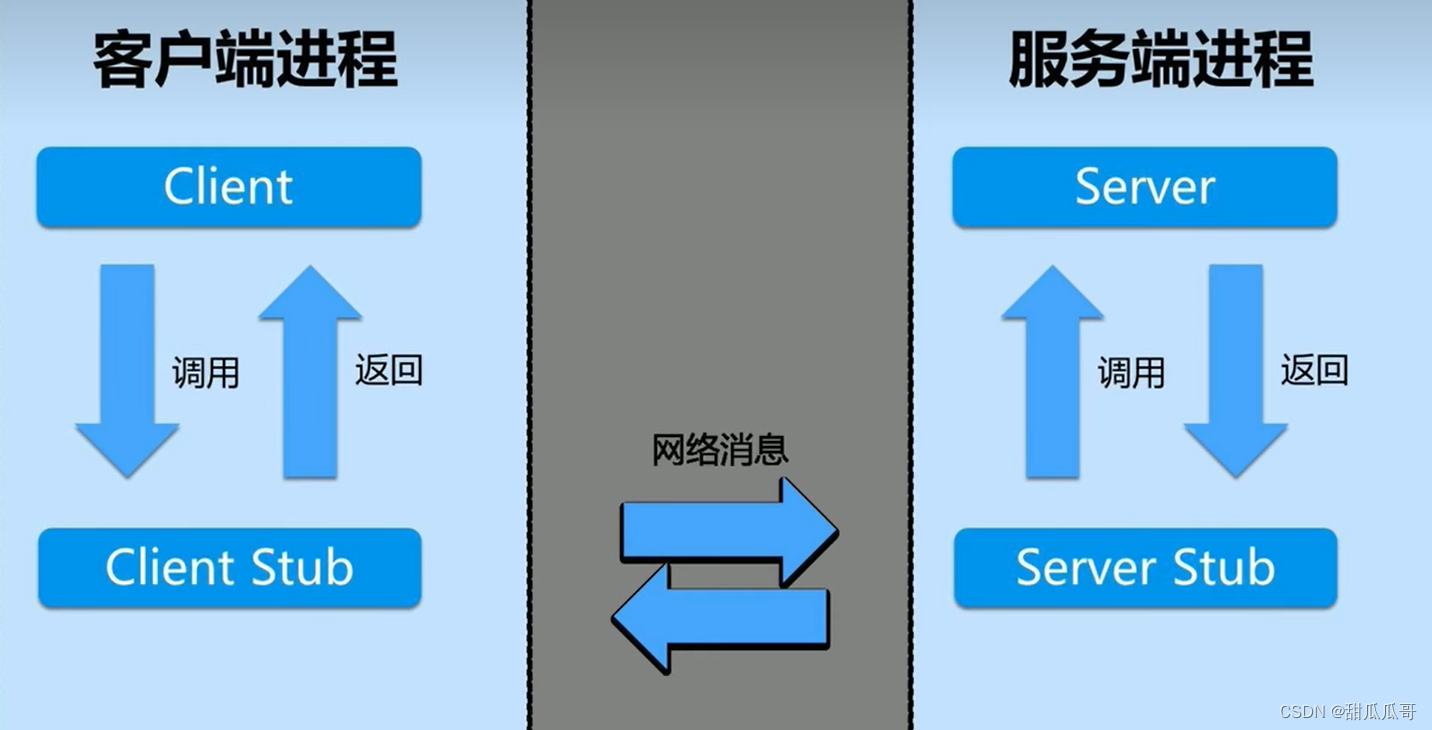
快速弄懂RPC
快速弄懂RPC 常见的远程通信方式远程调用RPC协议RPC的运用场景和优势 常见的远程通信方式 基于REST架构的HTTP协议以及基于RPC协议的RPC框架。 远程调用 是指跨进程的功能调用。 跨进程可以理解为一个计算机节点的多个进程或者多个计算机节点的多个进程。 RPC协议 远程过…...

ONVIF协议介绍
目录标题 一、 ONVIF协议简介(Introduction to ONVIF Protocol)1.1 ONVIF的发展历程(The Evolution of ONVIF)1.2 ONVIF的主要作用与优势(The Main Functions and Advantages of ONVIF) 二、 ONVIF协议的底…...

AI大模型内卷加剧,商汤凭什么卷进来
2023年,国内大模型何其多。 目前,已宣布推出或即将推出大模型的国内企业多达20余家,基本上能想到的相关企业都已入局。其中,既有资金雄厚的BAT、华为、字节等大厂,也有王慧文、王小川、周伯文等互联网大佬领衔的初创企…...
企业网络安全漏洞分析及其解决_kaic
摘要 为了防范网络安全事故的发生,互联网的每个计算机用户、特别是企业网络用户,必须采取足够的安全防护措施,甚至可以说在利益均衡的情况下不惜一切代价。事实上,许多互联网用户、网管及企业老总都知道网络安全的要性,却不知道网…...

Docker网络模式与cgroups资源控制
目录 1.docker网络模式原理 2.端口映射 3.Docker网络模式(41种) 1.查看docker网络列表 2.网络模式详解 4.Docker cgroups资源控制 1.CPU资源控制 2.对内存使用的限制 3.对磁盘IO的配置控制(blkio)的限制 4.清除docker占用…...
)
Linux/C++:基于TCP协议实现网络版本计算器(自定义应用层协议)
目录 Sock.hpp TcpServer.hpp Protocol.hpp CalServer.cc CalClient.cc 分析 因为,TCP面向字节流,所以TCP有粘包问题,故我们需要应用层协议来区分每一个数据包。防止读取到半个,一个半数据包的情况。 Sock.hpp #pragma on…...

并发之阻塞队列
阻塞队列 使用背景作用从阻塞队列中获取元素常用的三个方法往阻塞队列中存放元素的三种方式 使用背景 想要在多个线程之间传递数据,用一般的对象是不行的,比如我们常用的ArrayList和HashMap都不适合由多个线程同时操作,可能会造成数据丢失或…...
nodejs+vue 智能餐厅菜品厨位分配管理系统
系统功能主要介绍以下几点: 本智能餐厅管理系统主要包括三大功能模块,即用户功能模块和管理员功能模块、厨房功能模块。 (1)管理员模块:系统中的核心用户是管理员,管理员登录后,通过管理员功能来…...

MySQL NULL 值
NULL 值是遗漏的未知数据,默认地,表的列可以存放 NULL 值。 本章讲解 IS NULL 和 IS NOT NULL 操作符。 如果表中的某个列是可选的,那么我们可以在不向该列添加值的情况下插入新记录或更新已有的记录。这意味着该字段将以 NULL 值保存。 N…...

Python 机器人学习手册:1~5
原文:ILearning Robotics using Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线的时候,你最好…...

OpenCV(14)-OpenCV4.0中文文档学习2(补充)
相机校准和3D重建 相机校准 标定 findChessboardCorners() 它返回角点和阈值,如果成功找到所有角点,则返回 True。这些角落将按顺序放置(从左到右,从上到下)cornerSubPix()用以寻找图案,找到角点后也可以…...

八、express框架解析
文章目录 前言一、express 路由简介1、定义2、基础使用 二、express 获取参数1、获取请求报文参数2、获取路由参数 三、express 响应设置1、一般响应设置2、其他响应设置 四、express 防盗链五、express 路由模块化1、模块中代码如下:2、主文件中代码如下࿱…...
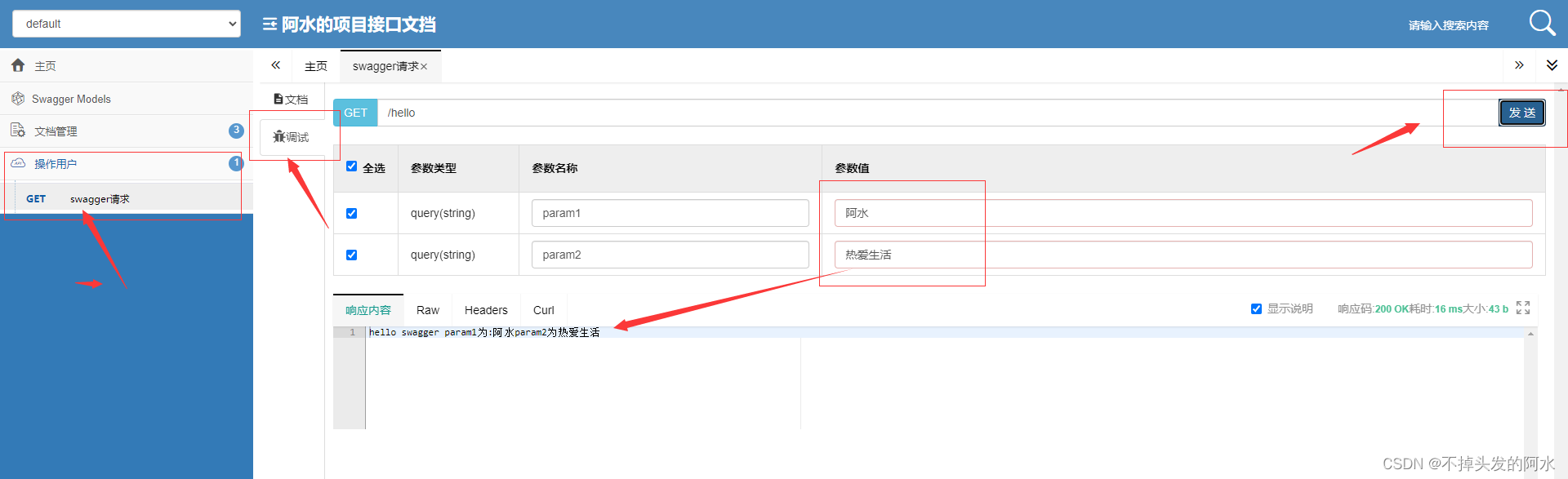
SpringBoot整合接口管理工具Swagger
Swagger Swagger简介 Springboot整合swagger Swagger 常用注解 一、Swagger简介 Swagger 是一系列 RESTful API 的工具,通过 Swagger 可以获得项目的⼀种交互式文档,客户端 SDK 的自动生成等功能。 Swagger 的目标是为 REST APIs 定义一个标…...

50+常用工具函数之xijs更新指南(v1.2.3)
xijs 是一款开箱即用的 js 业务工具库, 聚集于解决业务中遇到的常用的js函数问题, 帮助开发者更高效的进行业务开发. 目前已聚合了50常用工具函数, 接下来就和大家一起分享一下v1.2.3 版本的更新内容. 1. 添加将树结构转换成扁平数组方法 该模块主要由 EasyRo 贡献, 添加内容如…...

【DAY42】vue学习
const routes [ { path: ‘/foo’, component: Foo }, { path: ‘/bar’, component: Bar } ]定义路由的作用是什么 const routes 定义路由的作用是将每一个 URL 请求映射到一个组件,其中 path 表示请求的 URL,component 表示对应的组件。 通过 const…...

JavaScript小记——事件
HTML 事件是发生在 HTML 元素上的事情。 当在 HTML 页面中使用 JavaScript 时, JavaScript 可以触发这些事件。 Html事件 HTML 事件可以是浏览器行为,也可以是用户行为。 以下是 HTML 事件的实例: HTML 页面完成加载HTML input 字段改变…...
Windows逆向安全(一)之基础知识(八)
if else嵌套 这次来研究if else嵌套在汇编中的表现形式,本次以获取三个数中最大的数这个函数为例子,分析if else的汇编形式 求三个数中的最大值 首先贴上代码: #include "stdafx.h"int result0; int getMax(int i,int j,int k)…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
