题目3180:蓝桥杯2023年第十四届省赛真题-互质数的个数======及探讨互质专题
原题链接
https://www.dotcpp.com/oj/problem3162.html
想直接看题解的,跳转到第三次尝试即可。
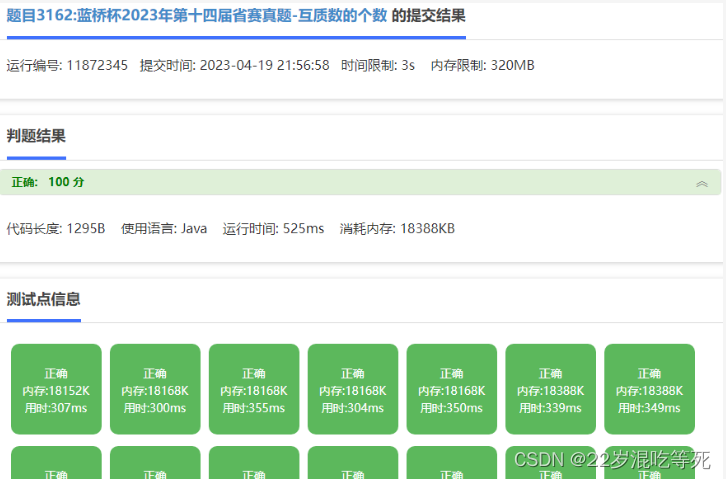
已AC。
解析:
(1)首先大家要知道什么叫互质:
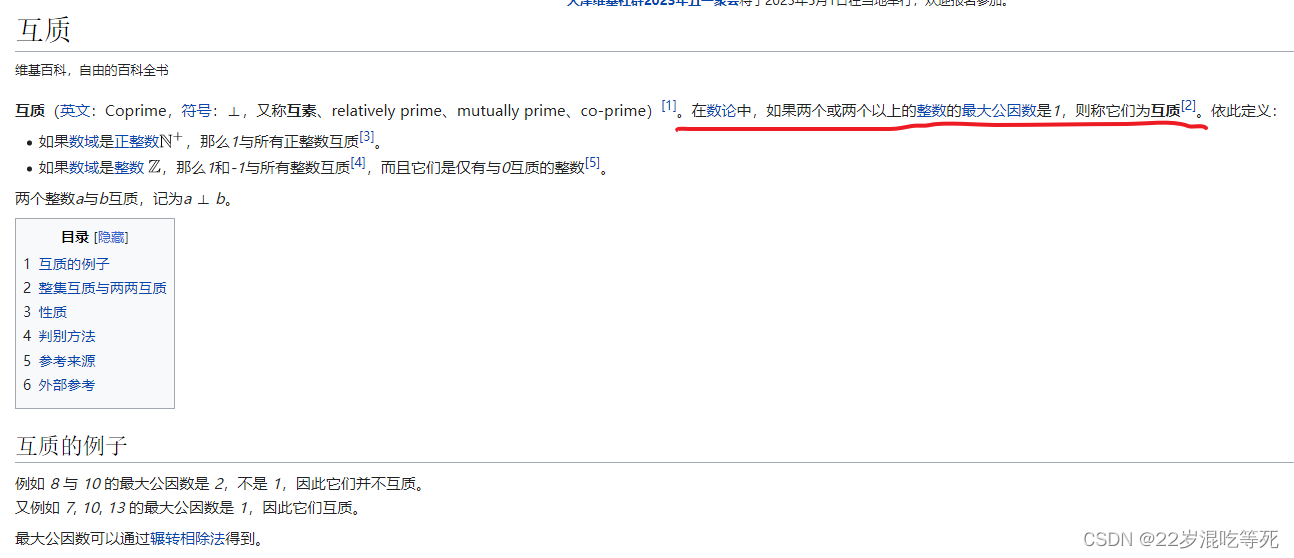
以及它们的性质:

欧拉函数
在数论中,对正整数n,欧拉函数φ(n)是小于或等于n的正整数中与n互质的数的数目。此函数以其首名研究者欧拉命名,它又称为φ函数(由高斯所命名)或是欧拉总计函数(totient function,由西尔维斯特所命名)。
例如φ(8) = 4,因为1,3,5,7均和8互质。
也可以从简化剩余系的角度来解释,简化剩余系(reduced residue system)也称既约剩余系或缩系,是m的完全剩余系中与m互素的数构成的子集,如果模m的一个剩余类里所有数都与m互素,就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中,从每一个类中各任取一个数作为代表组成的集合,叫做模m的一个简化剩余系。
(1,3,5,7)就构成了8的一个简化剩余系。
参考链接: https://zhuanlan.zhihu.com/p/151756874
第一次尝试代码:
package Dotcpp;import java.io.*;
import java.util.Scanner;public class 题目3180蓝桥杯2023年第十四届省赛真题_互质数的个数 {private static long mod = 998244353L;private static long a,b,ans;static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer st = new StreamTokenizer(br);static int nextLong() throws Exception {st.nextToken();return (int) st.nval;}static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));public static void main(String[] args) throws Exception {//Scanner scanner = new Scanner(System.in);a = nextLong();b = nextLong();long n = Euler_pow(a,b-1);long m = Euler(a);System.out.println((n*m%mod)%mod);}private static long Euler(long n) {long res = n;for (long i = 2; i * i <= n; ++i) {if (n % i == 0) {res = res / i * (i - 1);while (n % i == 0) {n /= i;}}}if (n > 1) {res -= res / n;}return res;}private static long Euler_pow(long a, long b) {long ans = 1;while (b != 0){if (b % 2 ==1){ans*=(a%mod)%mod;}a*=a%mod;a=a%mod;b /= 2;}return ans;}
}运行结果:
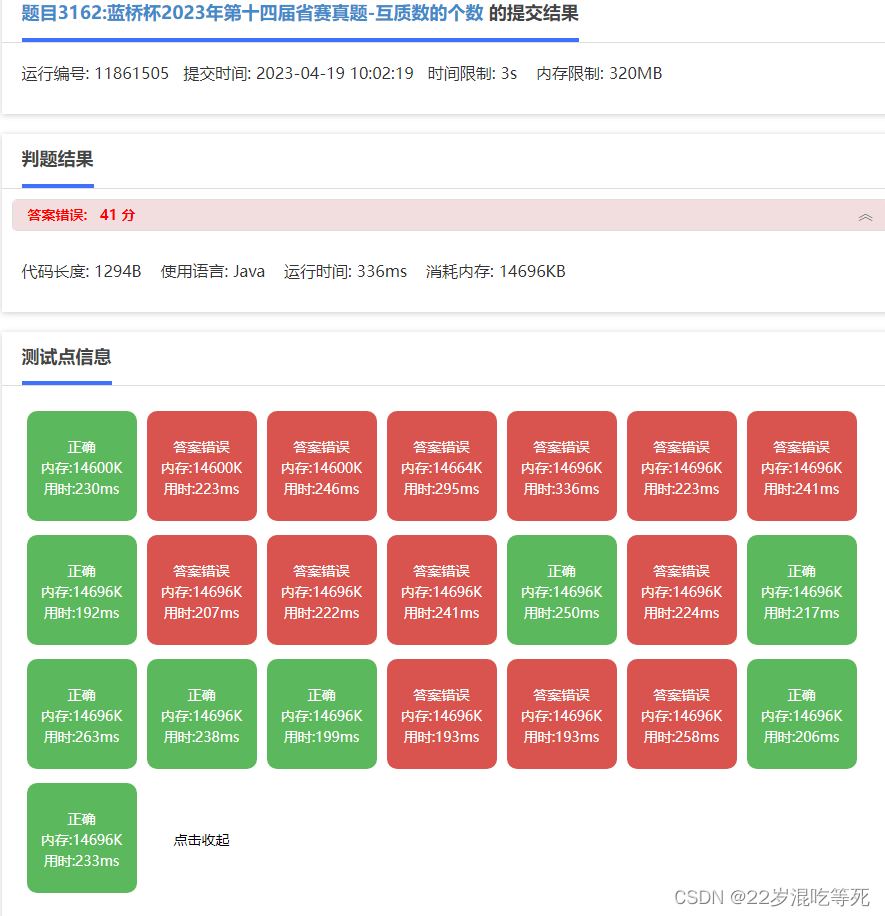
分析:
第二次尝试代码:
package Dotcpp;import java.util.Scanner;public class 题目3180蓝桥杯2023年第十四届省赛真题_互质数的个数__运行错误32分 {private static long mod = 998244353L;private static long a, b, res;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);a = scanner.nextInt();b = scanner.nextInt();long n = Euler_pow(a, b);res = n;for (int i = 2; i <= n / i; i++) {if (n % i == 0) {while (n % i == 0) {n /= i;n%=mod;}res = (res - res / i);res%=mod;}}if (n > 1) {res = (res - res / n);res%=mod;}System.out.println(res%=mod);}private static long Euler_pow(long a, long b) {long ans = 1;while (b > 0) {if ((b & 1) > 0) {ans = ((ans % mod) * (a % mod)) % mod;}a = ((a % mod) * (a % mod)) % mod;b /= 2;}return ans;}}运行结果:
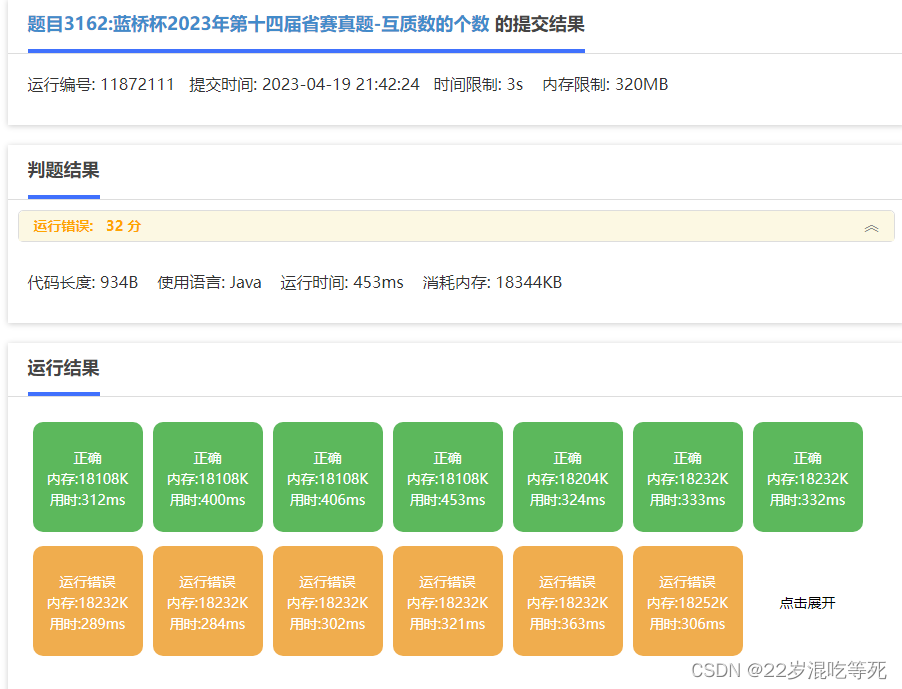
补充说明:
这第二次是我参考其他语言的代码,转化成Java来实现的。
如图可见:
感谢大佬提供的思路: https://blog.dotcpp.com/a/95823
分析:
当时一想,一种方法超时,一种方法会导致报错,两者结合一起,是不是可行呢。?
第三次尝试:
package Dotcpp;import java.io.*;
import java.util.Scanner;public class 题目3180蓝桥杯2023年第十四届省赛真题_互质数的个数 {private static long mod = 998244353L;private static long a,b,res;public static void main(String[] args) throws Exception {Scanner scanner = new Scanner(System.in);a = scanner.nextLong();b = scanner.nextLong();long n = Euler_pow(a,b);res = n;for (int i = 2; i <= n / i; i++) {if (n % i == 0) {while (n % i == 0) {n /= i;n%=mod;}res = (res - res / i);res%=mod;}}if (n > 1) {res = (res - res / n);res%=mod;}scanner.close();System.out.println(res%=mod);}private static long Euler(long n) {long res = n;for (long i = 2; i * i <= n; ++i) {if (n % i == 0) {res = res / i * (i - 1);while (n % i == 0) {n /= i;}}}if (n > 1) {res -= res / n;}return res;}private static long Euler_pow(long a, long b) {long ans = 1;while (b > 0) {if ((b & 1) > 0) {ans = ((ans % mod) * (a % mod)) % mod;}a = ((a % mod) * (a % mod)) % mod;b /= 2;}return ans;}
}结果:

分析:
相关文章:

题目3180:蓝桥杯2023年第十四届省赛真题-互质数的个数======及探讨互质专题
原题链接 https://www.dotcpp.com/oj/problem3162.html 想直接看题解的,跳转到第三次尝试即可。 已AC。 解析: (1)首先大家要知道什么叫互质: 以及它们的性质: 欧拉函数 在数论中,对正整…...

Java 文件操作
字符流-Writer和Reader用于读取文本-BufferedReader(new FileReader("path")) 读取文本文件-BufferedWriter(new FileWriter("path")) 写入到文本文件 字节流-InputStream和OutputStream图片、二进制文件-BufferedInputStream(new FileInputStream(new F…...

二叉树OJ题(C++实现)
文章目录 1.二叉树的层序遍历2. 二叉树的最近公共祖先3.二叉搜索树与双向链表4.从前序与中序遍历序列构造二叉树 1.二叉树的层序遍历 二叉树的层序遍历 OJ连接 主要思路是借助一个队列,将每一层的数据以size统计,当size为0时说明该层数据已经输入完&…...

grep -nr 命令查询字符串方式
grep -nr “搜索内容” 文件路径 其中: -n:显示行号-r:递归查找子目录中的文件“搜索内容”:要搜索的内容文件路径:要搜索的文件路径,可以是单个文件或目录路径(将会递归搜索该目录下的所有文…...

AgentAI+ChatGPT给出答案-为什么即时通讯需要心跳
序言 人工智能ChatGpt 结合系统化的问题拆解, 现在已经能够进行问题的拆解与自问自答, 预计未来很多的脑力工作要被释放了, 作为即时通讯的开发人员, 我问问专业的问题 为什么即时通讯需要心跳 先看产品界面与使用结果 问题拆解过程 执行任务1: 概念搜索 “Executing “Res…...
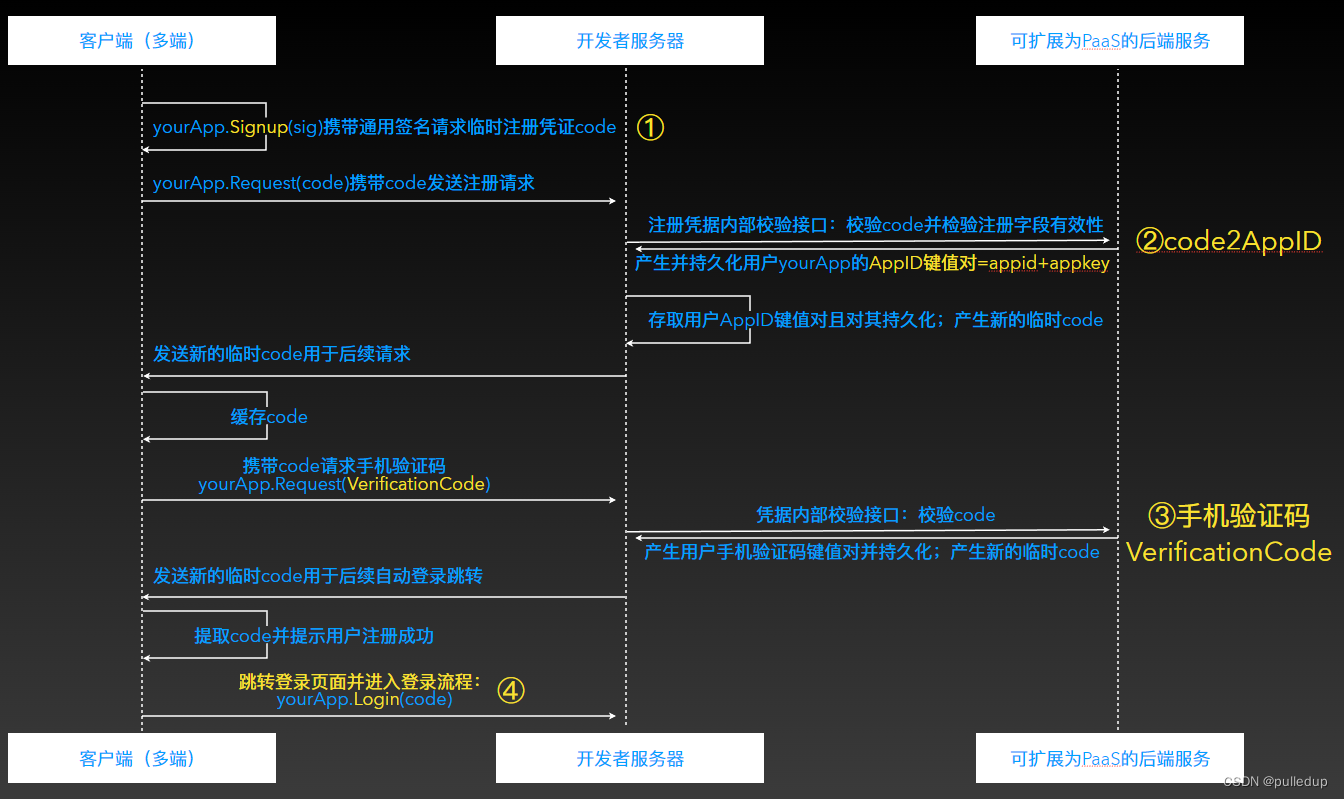
跨平台跨端的登录流程及其安全设计
跨平台跨端的登录流程及其安全设计 目录 跨平台跨端的登录流程及其安全设计 一、登录流程 1.1、登录流程时序图 1.2、三方App 登录 1.3、请求的路由守卫 二、注册流程 2.1、注册流程时序图 2.2、多因素认证 2.3、自动跳转登录页面 三、涉及的技术与安全 3.1、用户…...

如何在Java中创建临时文件?
在Java程序中,有时需要创建临时文件来暂存数据或者执行某些操作。Java提供了许多方式来创建临时文件。在本教程中,我们将介绍如何使用Java标准库来创建临时文件。 一、使用File.createTempFile()方法 Java标准库中的File类提供了createTempFile()方法来…...
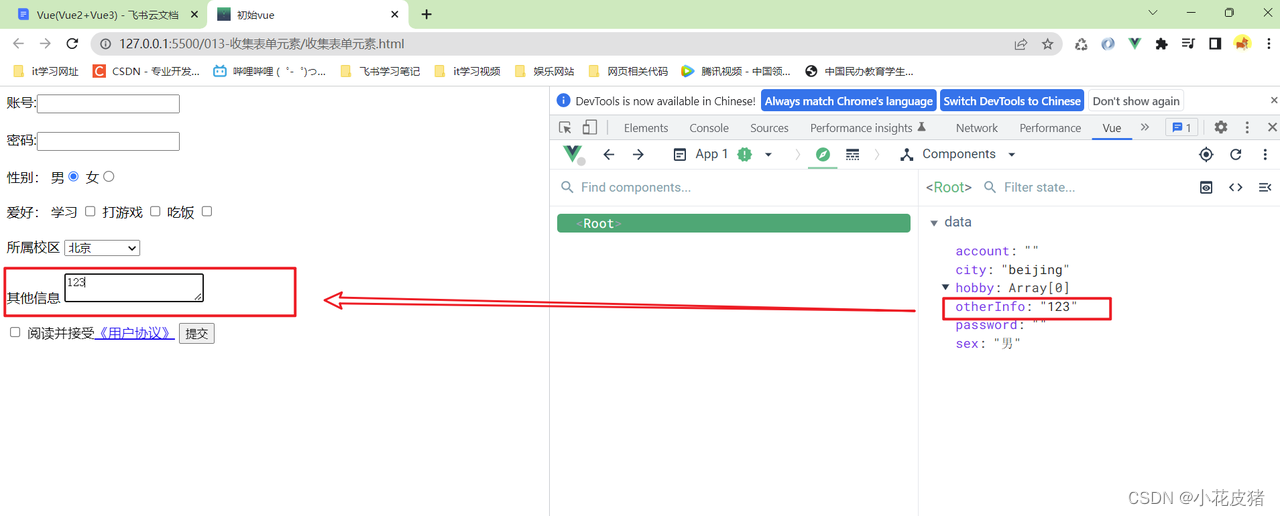
Vue表单基本操作-收集表单数据
收集表单数据 使用vue中的v-model收集表单里面的数据,不同的表单元素配合v-model会有不同的写法和技巧 本次的表单元素包括:文本框,单选,多选,下拉框,文本域 编写表单元素 首先编写表单元素,…...

Android 一个获取网址时间的Demo
Android 一个获取网址时间的Demo 文章目录 Android 一个获取网址时间的Demo通过一个网址获取时间的代码关于Android NTP 时间Android 同步时间代码 前段时间有个客户想用局域网同步Android 设备的时间,开发后把这个demo分享一下。 效果: 这里也获取了阿…...

ijkplayer解码流程源码解读
ijkplayer是一款基于ffmpeg的在移动端比较流行的开源播放器。FFmpeg是一款用于多媒体处理、音视频编解码的自由软件工程,采用LGPL或GPL许可证。 要想理解ijkplayer源码,首先得知道视频播放器的基本原理。 视频播放器播放一个互联网上的视频文件…...

2023年值得关注的3个品牌趋势,帮你弯道超车
2023年,大环境开放,压抑三年的消费蓄势待发,品牌如何唤醒消费者的、热情成了重中之重的大事。 春风和煦,万物生长。又到了各类品牌、各位营销人踌躇满志、斗志昂扬的时候了,浅析一下2023品牌宣传趋势,抓住…...
)
软考-高级项目管理(二十)
第20章 高级项目管理 (P572考0-2分选择 性价比很低) 在项目集管理中涉及的相关角色主要包括: 项目集发起人、项目集指导委员会、项目集经理、其他影响项目集的干系人 1.项目集发起人 项目集发起人和收益人是负责承诺将组织的资源应用于项目集,并致力于使项目集取得…...

RTMP协议深度解析:从原理到实践,掌握实时流媒体传输技术
目录标题 1. 引言1.1 流媒体传输技术的重要性1.2 为什么选择RTMP协议1.3 RTMP协议的发展与应用 2. RTMP协议基础2.1 RTMP协议简介2.2 RTMP协议与其他流媒体协议的比较2.3 RTMP协议的组成与工作原理 3. RTMP协议详解3.1 RTMP数据单元(Message)3.2 RTMP数据…...

2023mathorcup数学建模ABCD思路分析
更多思路分析,请看文末 A题:量子计算机在信用评分卡组合优化中的应用 题目提到了信用评分卡的组合优化,这是一个经典的优化问题。在这个问题中,需要通过不同的组合方式来选择不同的阈值,以达到最大化贷款利息收入和最…...

普通家庭,千万不要投入大量时间和金钱,让孩子去苦学和培养AI机器人编程了...
普通家庭,千万不要投入大量时间和金钱,让孩子去苦学和培养一些看似高端,实际却用处不大的兴趣爱好课程了,比如学钢琴、学音乐、学AI机器人编程这些兴趣爱好课程。 这些对孩子的成长其实意义并不大,尤其是AI机器人编程。…...
)
C++学习(day2)
文章目录 四. C中的字符串4.1 C支持两种风格的字符串4.2 string类型的赋值和初始化4.3 C风格和C风格的字符串互换4.4 string类中三个重要成员函数4.5 string类型的比较4.6 string类型的成员访问 at()6.8 string类型数据的输入 五、bool类型六、引用(reference&#…...

软考 - IP地址与网络划分
一.IP组成 1.1 首个八位字节规则 1.2 地址掩码 IP地址掩码 标准地址掩码 A类:255.0.0.0 前1个字节是网络号 后3个字节是主机号 B类:255.255.0.0 前2个字节是网络号 后2个字节是主机号 C类;255.255.255.0 前3个字节是网络号 后1个字节是主机号…...

Apifox软件的基础使用方式
Apifox软件的基础使用方式 简单方便的用途 该工具是接口在线调试工具,这里我给到连接供大家去官网下载,我个人觉得是比较于postman工具好用,提供的语言操作是中文版本的便于操作 下载和安装 https://apifox.com/?utm_sourcebaidu&ut…...

【Tensorflow】模型如何加载HDF文件数据集?
如果每个样本都被保存为一个单独的 HDF5 文件,可以使用 tf.data.Dataset.list_files 函数来创建一个文件名数据集,然后使用 tf.data.Dataset.interleave 函数来并行读取多个文件。 下面的示例展示了如何从多个 HDF5 文件中读取数据并创建一个 tf.data.D…...

校招又临近了,怎么在面试中应对设计模式相关问题呢?
夏天开始了,那么夏天结束时的毕业季也不远了。毕业是个伤感、期待而又略带残酷的时节,就像蜜桃无论成熟与否都会在这个时间被采摘,如果毫无准备就踏入社会,就会……马上变成低级社畜。所以说还是要早点为了毕业找工作做点准备&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
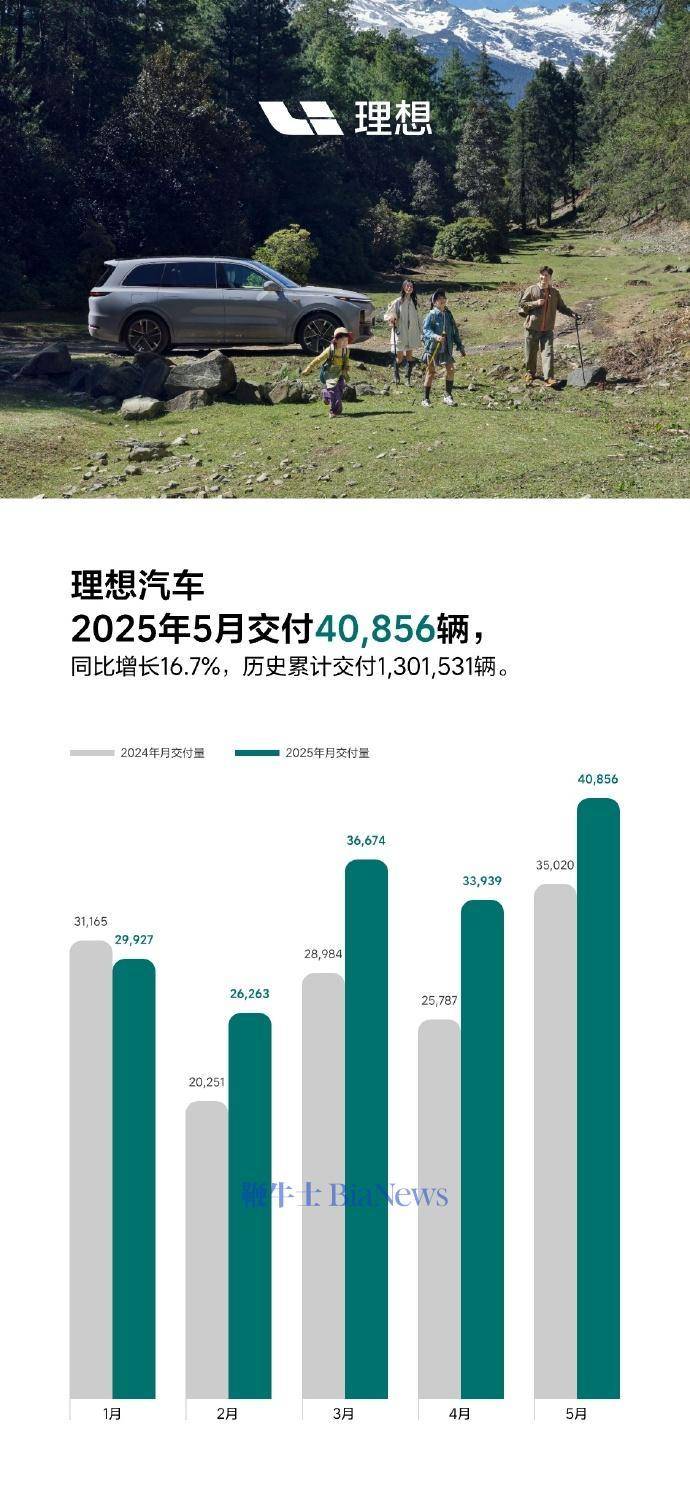
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
Web APIS Day01
1.声明变量const优先 那为什么一开始前面就不能用const呢,接下来看几个例子: 下面这张为什么可以用const呢?因为复杂数据的引用地址没变,数组还是数组,只是添加了个元素,本质没变,所以可以用con…...
