1187.使数组严格递增 学习记录
题目描述
给你两个整数数组 arr1 和 arr2,返回使 arr1 严格递增所需要的最小「操作」数(可能为 0)。
每一步「操作」中,你可以分别从 arr1 和 arr2 中各选出一个索引,分别为 i 和 j,0 <= i < arr1.length 和 0 <= j < arr2.length,然后进行赋值运算 arr1[i] = arr2[j]
如果无法让 arr1 严格递增,请返回 -1。
不会解,看题解之前没有可靠的思路
学习总结
思路总结
- 提炼关键信息
- 使数组
arr1严格递增,可以得到- 目的是替换之后使数组
arr1严格递增,所以不能有重复元素 - 选择数组
arr2中的元素进行替换,所以选择过程中不需要选择重复的元素进行替换 - 总结:可以对数组
arr2进行排序去重,方便操作
- 目的是替换之后使数组
- 以小窥大进行推导
n = arr1.length对于第[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EjuDr1zj-1682003137788)(null#card=math&code=i&id=urrlT)]个元素,有两种选择- 替换
- 不替换
- 如何去思考?
- 为了使数组严格递增那么,必须保证
arr1[i] > arr1[i-1] if arr1[i] > arr1[i-1]那么可以保留当前元素- 例外地:
if arr1[i] > arr1[i-1] + 1- 当前元素可以被替换成严格大于
arr1[i-1]的元素 - ex:
arr1 = [1, 5, 3, 6, 7] arr2 = [4, 3]5替换成3、3替换成4为满足题意的最优结果
- 当前元素可以被替换成严格大于
- 换言之,为了使数组严格递增,对于每一元素都需要进行两步操作
- 是否大于其前一个元素
- 是否能从已排序数组
arr2(从小到大)中找到一个小于当前元素且大于arr1[i-1]的元素
- 为了使数组严格递增那么,必须保证
- 需要返回最小操作数
- 直观地,对于每一个元素都进行替换的话,那么操作数是
n = arr1.length - 但是不一定有足够多的元素来提供使用
- 最多能够替换几次?
- 假设
n = 10 m = 20那么最多能够替换 10 次,因为有10个元素等待被替换 - 假设
n = 20 m = 11那么最多能够替换 11 次,因为有 11 次元素可以用来被替换 - 所以 最多的替换次数 是
j = Math.min(n, m)
- 假设
- 直观地,对于每一个元素都进行替换的话,那么操作数是
- 使数组
- 如何求解最终结果
- 通过学习题解了解到使用动态规划的方法
- 自己为什么没想起来?
- 还是太菜了,多学,多总结,多练
动态规划
思考角度——三个要素:状态、状态转移方程、边界确定
- 状态
- 从第一个元素开始,其是否选择交换是一个状态,每一个元素都会面临相同的情况
- 参数确定:定义
dp[i][j]表示第i个元素,经过j次替换,得到当前元素值- 最终结果:
dp[n][j] j <= Math.(m, n) 输出替换次数:j
- 最终结果:
- 什么时候选择不替换
arr1[i] > dp[i-1][j]当前元素大于第i-1个元素经过j次替换之后的结果- 有:
dp[i][j] = dp[i-1][j] if arr1[i] > dp[i-1][j]
- 有:
- 替换
- 从数组
arr2中找到元素arr2[k]使arr2[k] > dp[i-1][j-1]dp[i-1][j-1]表示第i-1个元素经过j-1次替换之后的结果- 有:
dp[i][j] = arr2[k]
- 从数组
- 状态转移
, & \text{if a r r 1 [ i ] > d p [ i − 1 ] [ j ] arr_1[i]>dp[i-1][j] arr1[i]>dp[i−1][j]}\
dp[i][j] = min(dp[i][j],&arr_2[k]), & \text{if arr_2[k]>dp[i-1][j-1]}
\end{cases}&id=X5oVX)
- 边界确定
- 为了方便计算
- [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cALoixEN-1682003137881)(null#card=math&code=dp[i][j]&id=hcEOV)]初始值都设置为
Integer.MAX_VALUE - 初始令
dp[0][0] = -1表示最小值
- [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cALoixEN-1682003137881)(null#card=math&code=dp[i][j]&id=hcEOV)]初始值都设置为
- 为了方便计算
代码
public int authorityWayOne(int[] arr1, int[] arr2) {// 对 数组2 进行排序Arrays.sort(arr2);// 去重List<Integer> list = new ArrayList<>();int prev = -1;for(int num : arr2) {if(num != prev) {list.add(num);prev = num;}}int n = arr1.length;int m = list.size();int[][] dp = new int[n+1][Math.min(m, n) + 1];// 初始化填充数据,方便计算for(int i = 0;i <= n;i++) {Arrays.fill(dp[i], Integer.MAX_VALUE);}dp[0][0] = -1;for(int i = 1;i <= n;i++) {for(int j = 0;j <= Math.min(m, n);j++) {if(arr1[i-1] > dp[i-1][j]) {// 这里不要搞混了dp[i][j] = arr1[i-1];}if(j > 0 && dp[i-1][j-1] != Integer.MAX_VALUE) {// 查找严格大于 dp[i-1][j-1] 的最小元素int idx = binary_search(list, j-1, dp[i-1][j-1]);if(idx != m) {dp[i][j] = Math.min(dp[i][j], list.get(idx));}}if(i == n && dp[i][j] != Integer.MAX_VALUE) {return j;}}}return -1;}private int binary_search(List<Integer> list, int low, int target) {int high = list.size();// 左闭右开区间while(low < high) {int mid = low + ((high - low) >> 1);if(list.get(mid) > target) {high = mid;} else {low = mid + 1;}}return low;}
优化一
- 数组原地去重
public int makeArrayIncreasing(int[] arr1, int[] arr2) {// 右边数组中选取元素,赋值给左边数组元素// 数组严格递增,所以数组中不能存在相同的元素// 对于 arr1 中的每一个元素都面临两种选择,换或者不换// --那么最终可以得到最终结果// --最小操作数一定存在这个过程中,现在问题是代码如何写// 首先 arr2 中的元素每一个只能用一次,为什么只能用一次?// 因为 要保证数组 arr1 严格递增// 所以可以对数组 arr2 进行排序Arrays.sort(arr2);// 那么现在问题是需要从 第一个元素开始判断换不换,// 定义 dp[i][j] 表示前 i 个元素进行 j 次替换之后末尾元素的最大值int n = arr1.length, m = 0;// arr2 中的重复元素不需要使用,所以进行去重for(int i = 1;i < arr2.length;i++) {if(arr2[m] != arr2[i]) {arr2[++m] = arr2[i];}}// 拿到不重复数组的长度m++;// 拿到之后呢?// 最大的交换次数是多少?- 交换所有元素int changeNum = Math.min(m, n);// 那么接下来呢? 定义dp 一维:元素个数,二维:交换次数int[][] dp = new int[n+1][changeNum+1];// 初始化最大值for(int i = 0;i <= n;i++) {Arrays.fill(dp[i], Integer.MAX_VALUE);}dp[0][0] = -1;for(int i = 1;i <= n;i++) {for(int j = 0;j <= Math.min(i, m);j++) {// 如果当前元素大于前一个元素if(arr1[i - 1] > dp[i-1][j]) {dp[i][j] = arr1[i - 1];}// 尝试交换.if(j > 0 && dp[i-1][j-1] != Integer.MAX_VALUE) {// 查找严格大于 dp[i-1][j-1] 的元素// 这里涉及到二分查找,如何才能找到 严格大于 dp[i-1][j-1] 的元素int idx = binary_search(arr2, j-1, dp[i-1][j-1], m);if(idx != m) {dp[i][j] = Math.min(dp[i][j], arr2[idx]);}}if(i == n && dp[i][j] != Integer.MAX_VALUE) {return j;}}}return -1;}private int binary_search(int[] arr, int j, int prev, int m) {// 左闭右开区间查找int left = j,right = m;while(left < right) {int mid = left + ((right - left) >> 1);if(arr[mid] > prev) {right = mid;} else {left = mid+1;}}return left;}
参考
官方题解
https://leetcode.cn/problems/make-array-strictly-increasing/solution/zui-chang-di-zeng-zi-xu-lie-de-bian-xing-jhgg/
相关文章:

1187.使数组严格递增 学习记录
题目描述 给你两个整数数组 arr1 和 arr2,返回使 arr1 严格递增所需要的最小「操作」数(可能为 0)。 每一步「操作」中,你可以分别从 arr1 和 arr2 中各选出一个索引,分别为 i 和 j,0 < i < arr1.l…...
权限控制_SpringSecurity
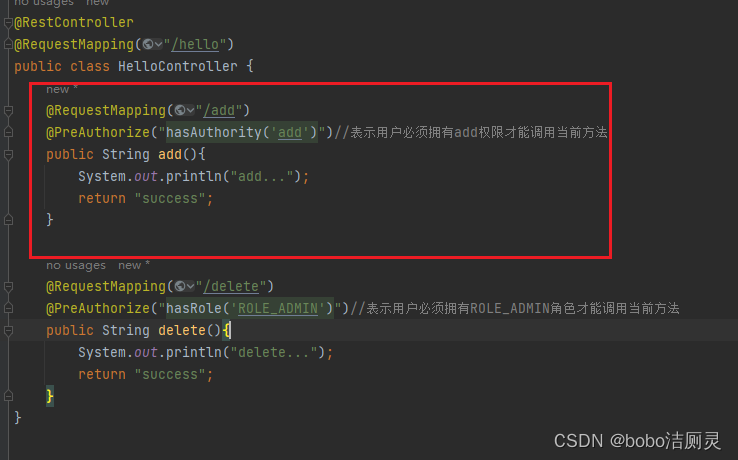
认证-授权 认证:系统提供的用于识别用户身份的功能,通常提供用户名和密码进行登录其实就是在进行认证,认证的目的是让系统知道你是谁。 授权:用户认证成功后,需要为用户授权,其实就是指定当前用户可以操作…...

2023年最系统的自动化测试,测试开发面试题,10k以下不建议看
鉴于现在严峻的就业形势,千万大学生即将出新手村,今天给大家打包好了2023最能避免薪资倒挂的《面试圣经》。不经一番寒彻骨,怎得梅花扑鼻香。这份面试题,与君共勉! 一、开场白 Q:简单自我介绍一下吧 Q:项…...
今年SMETA审核费用即将涨价
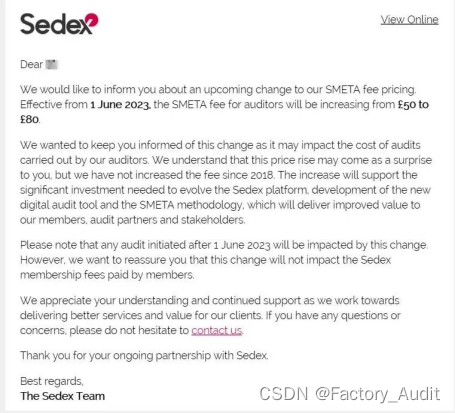
【今年SMETA审核费用即将涨价】 SMETA全称( Sedex Members Ethical Trade Audit ),即Sedex会员社会道德贸易审核,它是Sedex发起的一种负责任的供应链审计方法/项目。 Sedex是一个全球性的责任商业平台,SMETA是审核方法…...
基于贝叶斯优化CNN-LSTM混合神经网络预测(Matlab代码实现)
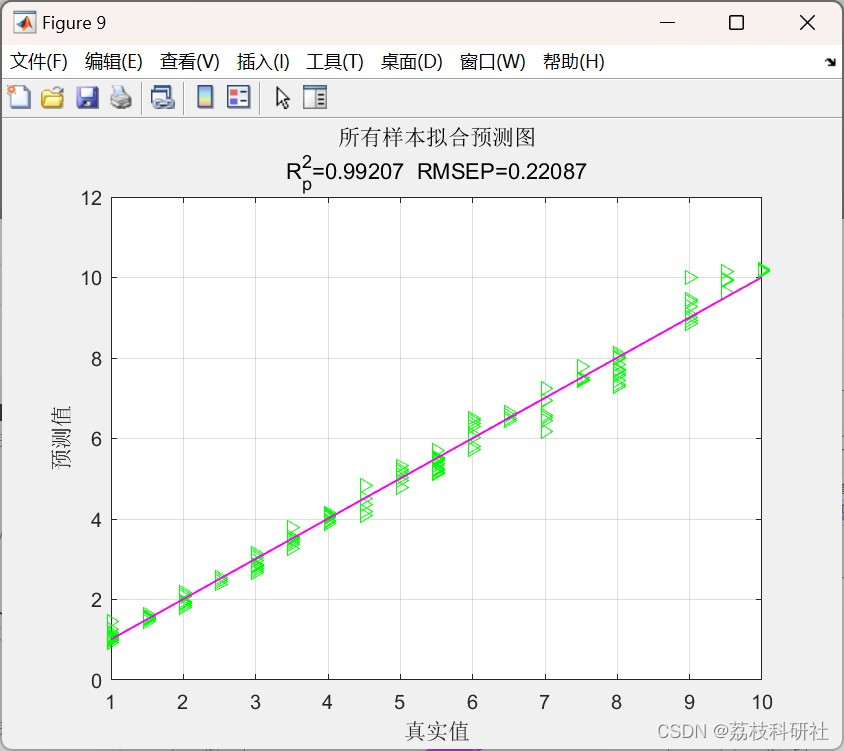
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
基于深度学习和生理信号的疾病筛查:个体内和个体间研究的价值与应用
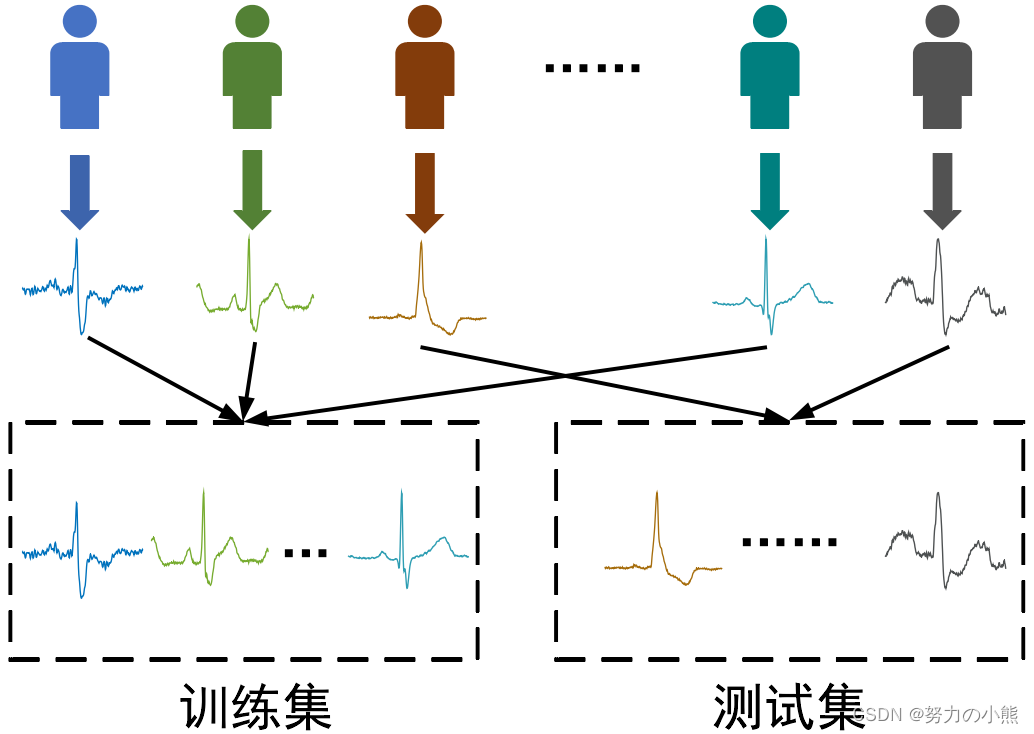
一、引言 随着深度学习技术的飞速发展,基于生理信号的疾病筛查和诊断方法在医学领域得到了广泛应用。这些方法通常利用个体内和个体间的生理信号数据,通过训练深度学习模型实现疾病的自动识别和预测。本文将讨论个体内和个体间研究在这一领域的价值和应…...
现在有t1,t2,t3三个线程,实现t1,t2线程同步执行,然后再执行t3线程,使用Java实现该程序
目录 1、利用CountDownLatch 2、利用Future 最近在面试的时候,经常遇到这个题目,首先从题目上看,就知道考察的是多线程方面知识,我第一次看到这个题目的时候,就想到了使用CountDownLatch这个计数器来实现,…...

83.qt qml-初步学习2D粒子影响器(二)
由于QmlBook in chinese翻译过来的文字有些比较生疏难于理解,所以本章在它的基础上做些个人理解,建议学习的小伙伴最好配合QmlBook in chinese一起学习。 QML粒子所有类型: Qt Quick Particles QML Types | Qt Quick 6.5.0 Affector类型: Attractor QML Type | Qt Quick 6.5.…...

4.17-4.18学习总结
MD5 MD5: 1、压缩性 2、容易计算 3、抗修改性 4、弱抗碰撞 5、强抗碰撞 为什么需要MD5? 存储一些敏感信息的时候,如果不进行加密会出现安全问题。 例如:系统登录的密码,如果数据库中的密码采用明文,一旦数据库泄…...
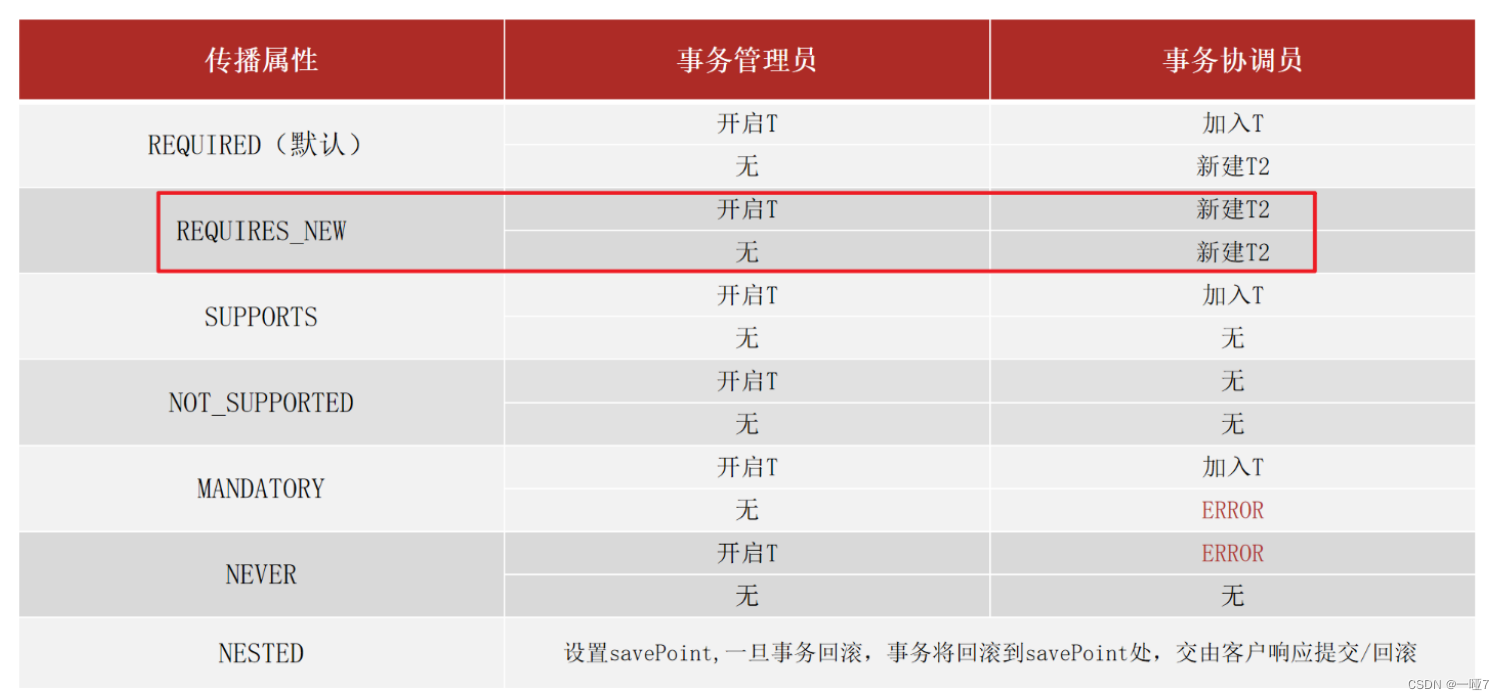
Spring事务
事务作用: 事务作用:在数据层保障一系列的数据库操作同成功同失败Spring事务作用:在数据层或 业务层 保障一系列的数据库操作同成功同失败 Spring为了管理事务,提供了一个平台事务管理器PlatformTransactionManager commit是用来提…...

Linux新的设备或分区挂载到系统中mount使用方法
如果想将一个新的设备或分区挂载到系统中,可以按照以下步骤进行操作: 确定要挂载的设备或分区的设备名,例如 /dev/sdb1。 创建挂载点,可以在任何目录下创建一个新目录作为挂载点,例如 /mnt/mydevice。 sudo mkdir /mn…...

移动硬盘损坏如何恢复数据
移动硬盘一种小巧便携的存储介质,可用于各电脑之间交换大容量数据,可以随时插拔,进行高速传输数据。但有好也有坏,在我们使用中也会出现一些移动硬盘损坏故障,比如说提示格式化、硬盘分区丢失、误格式化、文件误删除等…...

Material Design:为你的 Android 应用提供精美的 UI 体验
Material Design:为你的 Android 应用提供精美的 UI 体验 介绍 Material Design 概念:介绍 Material Design 是 Google 推出的一种设计语言,用于创建现代、美观、直观且一致的用户界面。解释 Material Design 的基本原则,包括材料…...

springboot+vue学生毕业离校系统(源码+说明文档)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的学生毕业离校系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 💕💕作者:风…...

【Android入门到项目实战-- 6.2】—— 如何访问其他应用程序的数据?
目录 一、ContentResolver基本用法 如何查询? 如何向表中添加一条数据? 如何更新这条新添加的数据? 如何删除这条数据? 二、读取系统联系人 要想你的APP访问其他应用程序的数据,需要使用内容提供器,下面使…...

【100个 Unity实用技能】 | InputField输入框组件实现输入限制,只能输入中文或特殊字符等
🎬 博客主页:https://xiaoy.blog.csdn.net 🎥 本文由 呆呆敲代码的小Y 原创,首发于 CSDN🙉 🎄 学习专栏推荐:Unity系统学习专栏 🌲 游戏制作专栏推荐:游戏制作 &…...

倍数+路径之谜
倍数 :用户登录https://www.lanqiao.cn/problems/583/learning/?page5&first_category_id1&sortstudents_count 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 请问在 1 到 2020 中,有多少个…...

【Unity渲染】URP透明物体自身渲染穿插异常问题
背景: 对于URP中的某个物体,我们如果希望他正反面都可以被渲染。 通常会有两种解决方案: 1.将网格设置为双面网格。(此种情况Mesh.RecalculateNormals计算结果可能会异常,解决可参考网格法线生成异常解决࿰…...

c/c++:指针,指针定义和使用,指针大小4字节,野指针,空指针*p=NULL
c/c:指针,指针定义和使用,指针大小4字节,野指针,空指针*pNULL 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,此时学会c的话, 我所知道的周边的会c的同学…...

CAS实现原⼦操作的三⼤问题,该如何解决?
目录 1、ABA问题 2.循环时间长开销大 3、只能保证一个共享变量的原子操作 总结: CAS(Compare-and-Swap)是一种用于实现原子操作的技术,但是它存在着三个主要的问题:ABA问题、循环时间长开销大、只能保证一个共享变…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...
