当前位置：首页 > news >正文

【最优化理论】线性规划

news 2026/1/28 14:41:03

文章目录

什么是线性规划（Linear Programming，LP）？
线性规划的标准形式
非标准形LP模型转化为标准形LP模型
基本概念
- 基本解&基矩阵&基变量&非基变量
- 基本可行解&可行基矩阵&非退化的基本可行解&退化的基本可行解
- 基本可行解存在性
- 求基本可行解
- - 示例：求基本可行解
- 求最优解
- - 方法一（暴力枚举）：求出所有基本可行解找最小
  - 方法二（迭代）：从一个基本可行解跳转到一个目标函数值更小的基本可行解
多面体
- 多面体基本性质
- 多面体的极点
- - 示例：求极点
- 多面体S有多少个极点？- 有限个 & 最多 $C_n^m$
- 多面体的方向
- 多面体的极方向
- - 多面体的极方向有多少个？- 有限个
  - 示例：求极方向
多面体分解定理
- 多面体分解定理有什么作用？
- - 重新表示可行集
  - 重新定义线性规划问题
  - - 为什么 $min⁡∑λiCTxi\min \sum \lambda_i C^Tx_i$ 等价于 $min C^Tx_i,i=1,...,k$ ？
  - 何时有最优解？
  - 最优解是什么？
单纯形法
- 基本思想
- 原理
- 方法
- 1 确定出基变量和出基向量的下标
- 2 确定进基变量和进基向量的下标
- 3 确定进基变量的值
- - 终止条件
单纯形法计算步骤
单纯形法表格形式

什么是线性规划（Linear Programming，LP）？

目标函数为决策变量的线性函数，同时约束条件为线性等式或线性不等式约束。

线性规划的标准形式

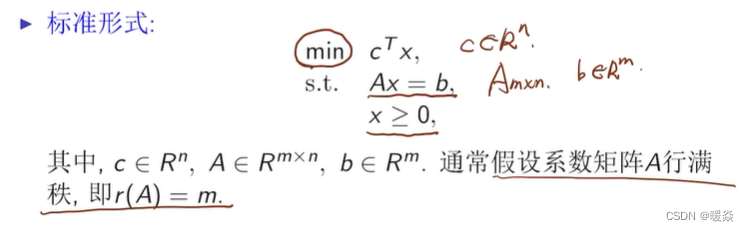
在这里插入图片描述

非标准形LP模型转化为标准形LP模型

在这里插入图片描述

基本概念

在这里插入图片描述

基本解&基矩阵&基变量&非基变量

基本可行解&可行基矩阵&非退化的基本可行解&退化的基本可行解

在这里插入图片描述

基本可行解存在性

在这里插入图片描述

求基本可行解

求基本可行解<=>求极点<=>求可行基矩阵<=> $A_{m*n}$ 矩阵m个线性无关列
在这里插入图片描述

示例：求基本可行解

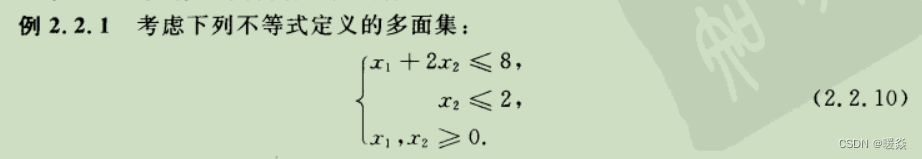
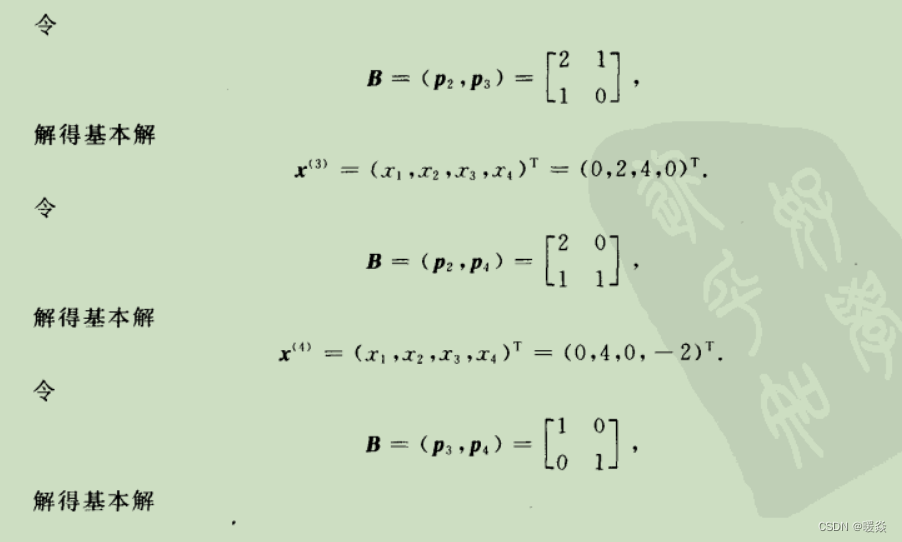
在这里插入图片描述

求最优解

方法一（暴力枚举）：求出所有基本可行解找最小

求出所有基本可行解（即求极点）。
代入目标函数找出最小极点（该最小极点即为最优解，因为最优解一定在极点取得）。

方法二（迭代）：从一个基本可行解跳转到一个目标函数值更小的基本可行解

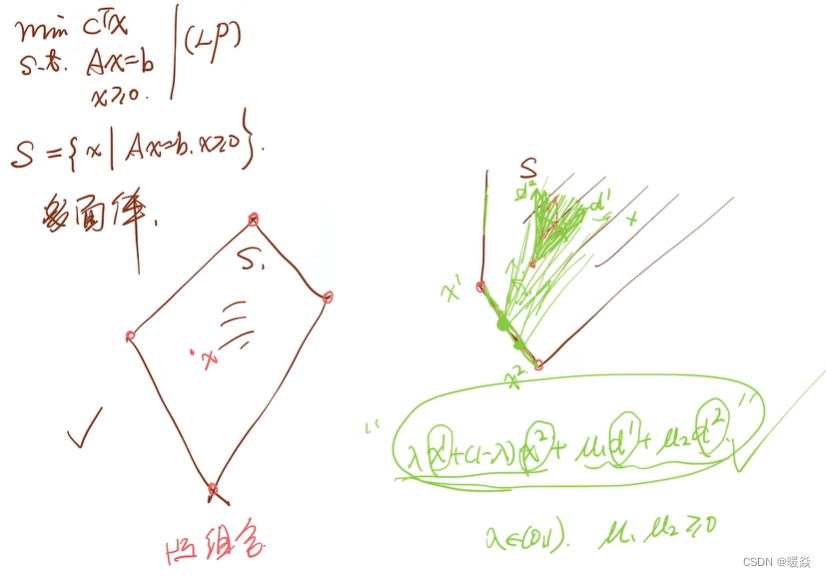
在这里插入图片描述

多面体

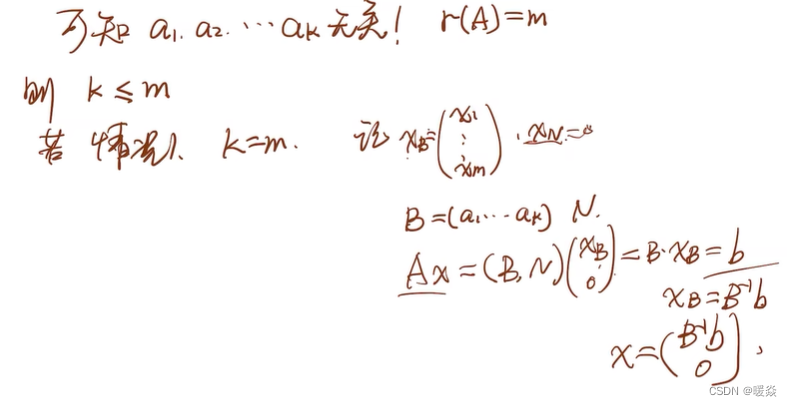
在这里插入图片描述

多面体基本性质

在这里插入图片描述

多面体的极点

在这里插入图片描述

x若是极点，正分量对应的A的列一定线性无关。

示例：求极点

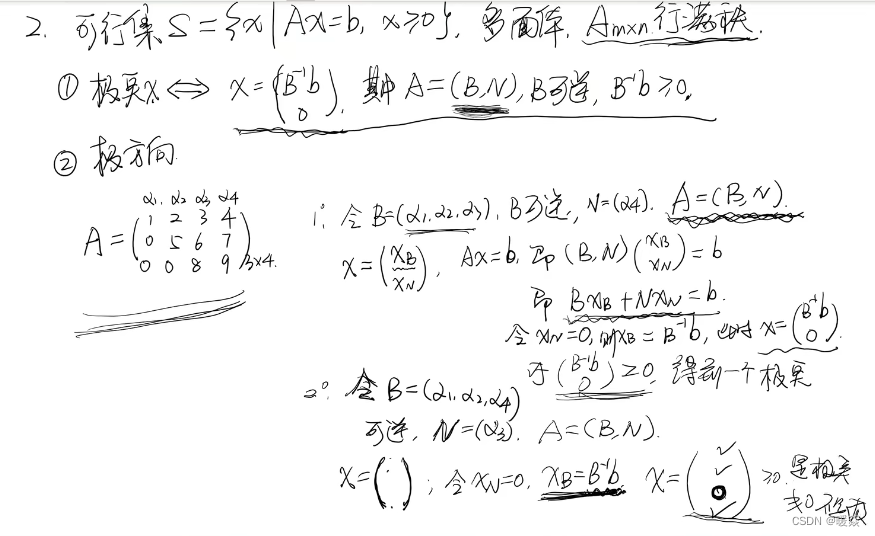
在这里插入图片描述

多面体S有多少个极点？- 有限个 & 最多 $C_n^m$

最多有 $C_n^m$ 个极点，一般都少于 $C_n^m$ ，有两个原因。
原因1：从n个列中选出m列不一定线性无关。
原因2：即使这m列线性无关，其组成的B也不一定满足 $B−1b≥0B^{-1}b\ge 0$ 。

多面体的方向

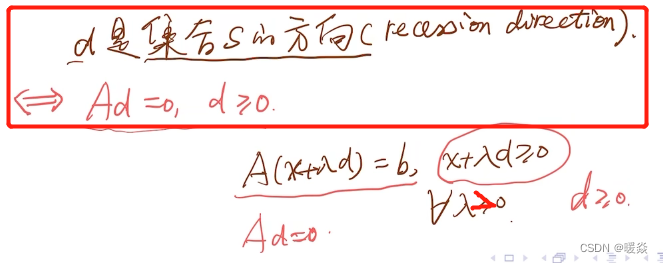
在这里插入图片描述

多面体的极方向

在这里插入图片描述

多面体的极方向有多少个？- 有限个

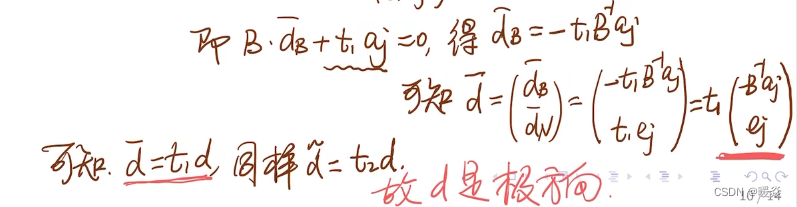
在这里插入图片描述

示例：求极方向

在这里插入图片描述
d≥0

多面体分解定理

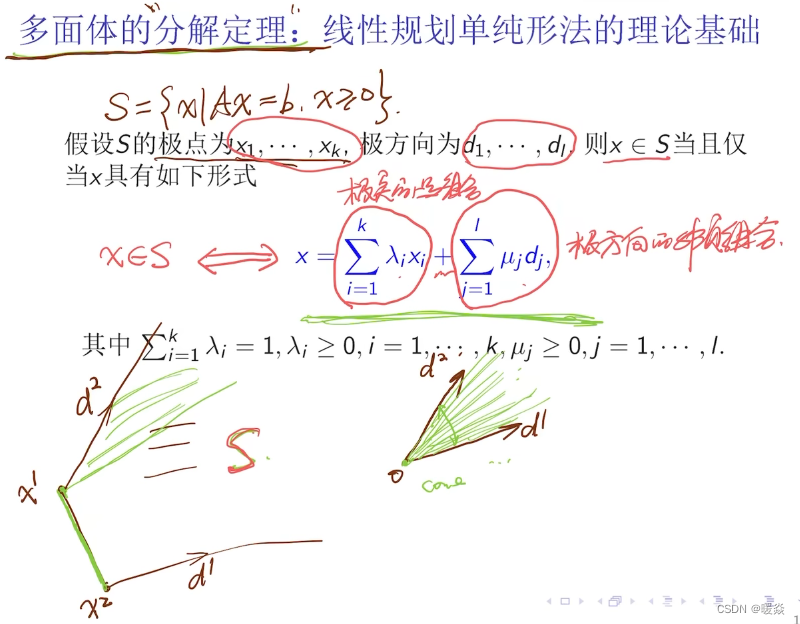
在这里插入图片描述

多面体分解定理有什么作用？

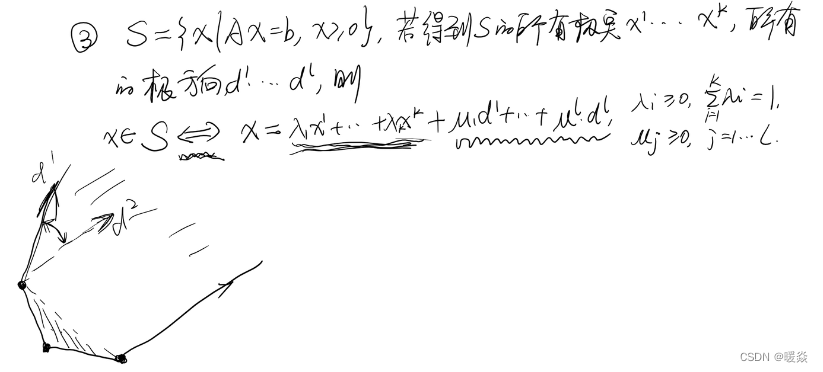
在这里插入图片描述

重新表示可行集

在这里插入图片描述

重新定义线性规划问题

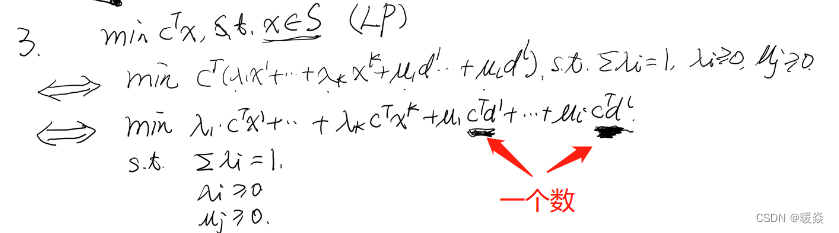
在这里插入图片描述

为什么 $min⁡∑λiCTxi\min \sum \lambda_i C^Tx_i$ 等价于 $min C^Tx_i,i=1,...,k$ ？

求 $min C^Tx_i，i=1,...,k$ ，找到最小 $x_r$ 就是最优值点，令 $min⁡∑λiCTxi\min \sum \lambda_i C^Tx_i$ 中 $λr=1\lambda_r=1$ 其他的λ都为0， $C^Tx_r$ 就是最优值。

何时有最优解？

$CTdj≥0C^Td_j \ge 0$ 时，存在最优解。

$CTdj<0C^Td_j \lt 0$ 时，无解。

最优解是什么？

最优解一定在极点上取到。

$min C^Tx_i，i=1,...,k$ ，找到最小 $x_r$ 就是最优值点， $C^Tx_r$ 就是最优值。

单纯形法

在这里插入图片描述

基本思想

在这里插入图片描述

原理

实现基本可行基的转化

方法

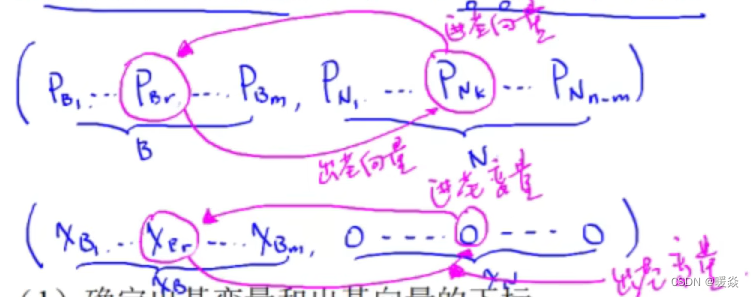
在这里插入图片描述

从初始基本可行解出发，求一个改进的基本可行解。

1 确定出基变量和出基向量的下标

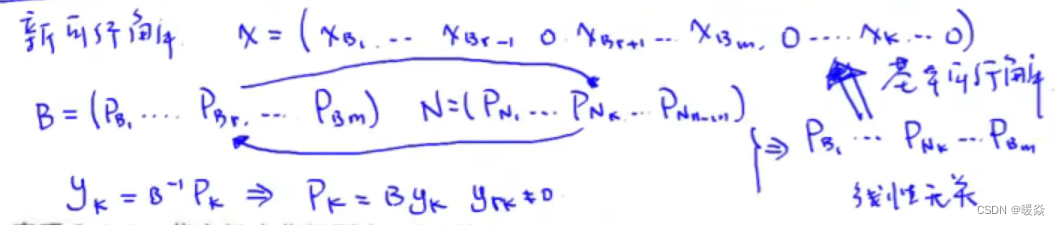
2 确定进基变量和进基向量的下标

3 确定进基变量的值

目标函数值只与非基变量有关。
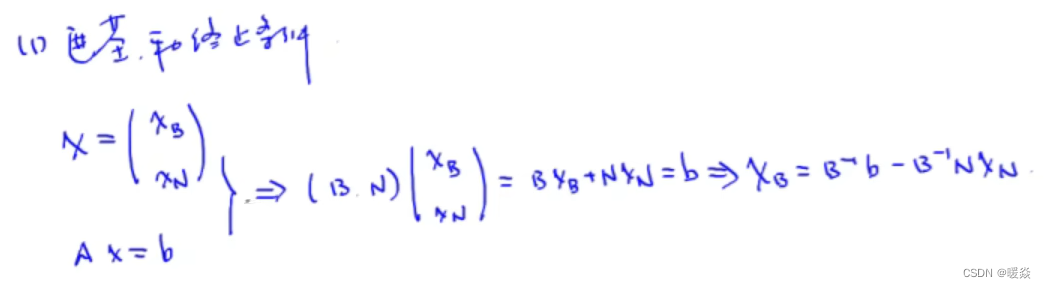
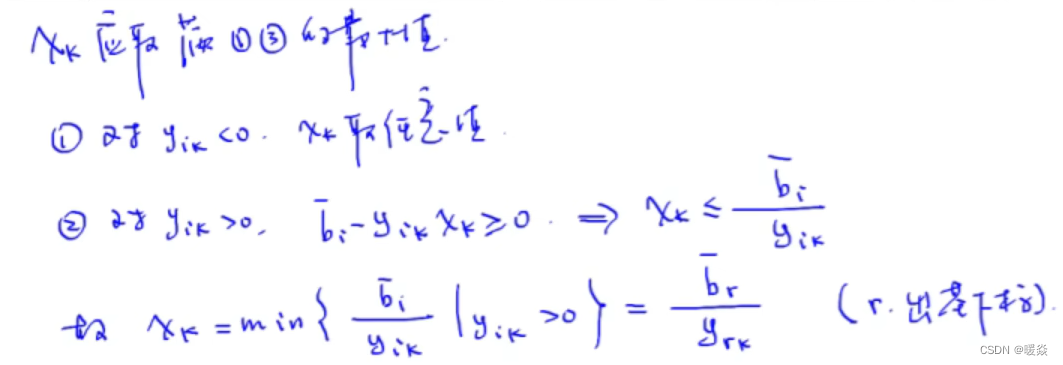
在这里插入图片描述

在这里插入图片描述

终止条件

在这里插入图片描述

单纯形法计算步骤

在这里插入图片描述

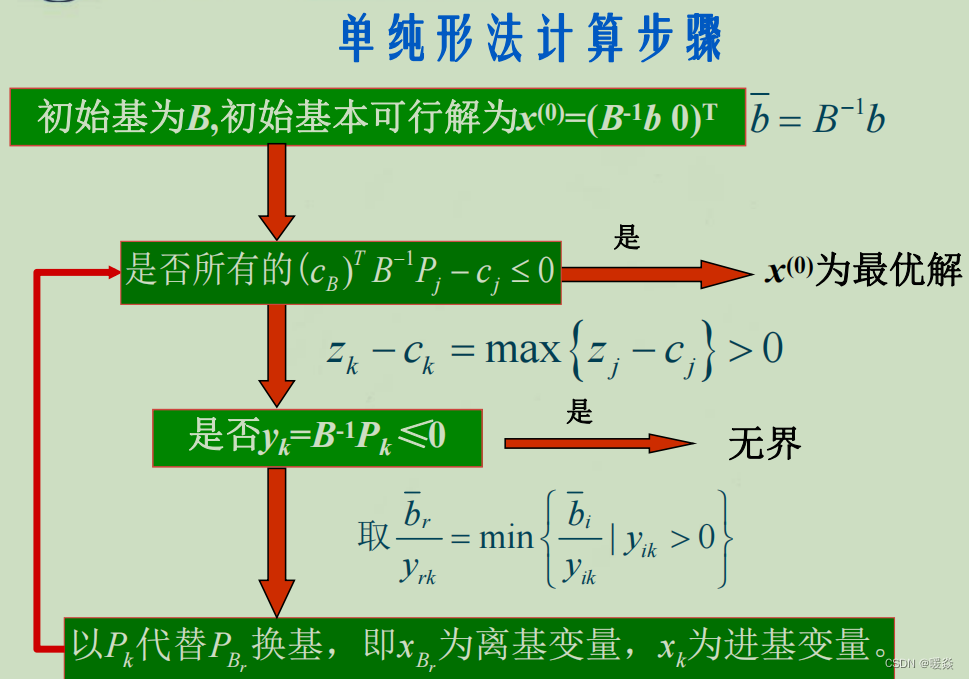
单纯形法表格形式

【最优化理论】线性规划

文章目录什么是线性规划（Linear Programming，LP）？线性规划的标准形式非标准形LP模型转化为标准形LP模型基本概念基本解&基矩阵&基变量&非基变量基本可行解&可行基矩阵&非退化的基本可行解&退化的基本可行…...

编程日记 2023/5/28 20:42:47

数据库测试的认知和分类

数据库测试的认知和分类目录：导读系统测试集成测试单元测试功能测试数据库性能性能优化分4部分安全测试现在的软件系统，尤其是业务应用系统，后台都连接着一个数据库。数据库中存储了大量的数据，数据库的设计是否…...

编程日记 2023/5/15 18:34:14

MQ中间件概念一览

一、概述 1. 大多应用中，可通过消息服务中间件来提升系统异步通信、扩展解耦能力 2. 消息服务中两个重要概念： 消息代理（message broker）和目的地（destination） 当消息发送者发送消息以后，将由…...

编程日记 2023/5/17 2:42:16

爱尔兰公司注册要求及条件

简介： 爱尔兰是一个高度发达的资本主义国家，也是欧盟、经济合作与发展组织、世界贸易组织和联合国的成员国。并且也是世界经济发展速度快的国家之一，因经济发达赢得了“欧洲小虎”的美誉。总体来看，爱经济发展势头趋稳&#xff0c…...

编程日记 2023/5/29 13:31:59

Java中如何打印对象内存地址？

先看一个简单的程序，一般我们打印对象，大部分是下面的情况，可能会重写下toString()方法，这个另说 Frolan frolan new Frolan(); System.out.println(frolan);// 输出结果 com.test.admin.entity.Frolan2b80d80f这个结果其实是调…...

编程日记 2023/5/31 0:47:33

CF1707E Replace

题目描述给定一个长为 nnn 的序列 a1,…,ana_1,\ldots,a_na1,…,an，其中对于任意的 iii 满足 1≤ai≤n1 \leq a_i \leq n1≤ai≤n。定义一个二元组函数如下： f((l,r))(min⁡{al,…,ar},max⁡{al,…,ar})(l≤r)f((l,r))(\min\{a_l,\ldots,a_r\}…...

编程日记 2023/5/29 2:50:18

【Hello Linux】Linux工具介绍（make/makefile git）

作者：小萌新专栏：Linux 作者简介：大二学生希望能和大家一起进步！ 本篇博客简介：介绍Linux的常用工具make/makefile git Linux项目自动化构建工具 – make/Makefile 背景会不会写Makefile 从侧面说明了一个人是否具…...

编程日记 2023/5/10 12:00:02

享元模式flyweight

享元模式属于结构型模式。享元模式是池技术的重要实现方式，它可以减少重复对象的创建，使用缓存来共享对象，从而降低内存的使用。细粒度的对象其状态可以分为两种：内部状态和外部状态。应用场景系统存在大量相似或相同的对象。外部…...

编程日记 2023/5/15 8:59:03

Pulsar

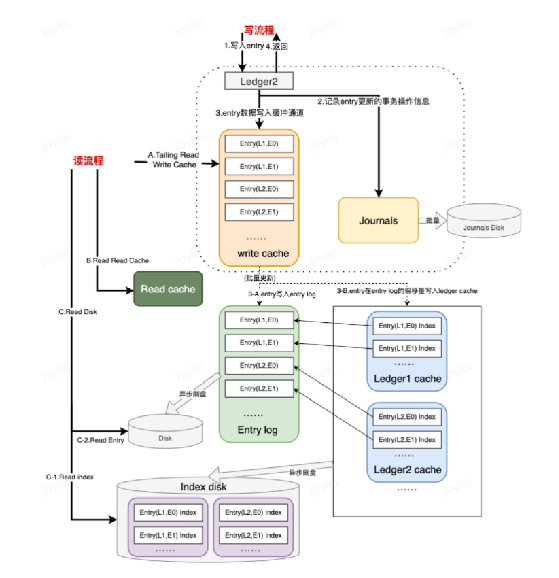
一、简介Apache Pulsar是Apache软件基金会顶级项目，是下一代云原生分布式消息流平台，集消息、存储、轻量化函数式计算为一体，采用计算与存储分离架构设计，支持多租户、持久化存储、多机房跨区域数据复制，具有强一致性、…...

编程日记 2023/5/30 5:40:58

项目介绍 + 定长内存池设计及实现

你好，我是安然无虞。文章目录项目介绍当前项目做的是什么?技术栈内存池是什么?池化技术内存池内存池主要解决的问题malloc定长内存池学习目的定长内存池设计项目介绍当前项目做的是什么? 这个项目是实现一个高并发的内存池, 它的原型是 Google 的一个开源项…...

编程日记 2023/5/27 11:48:20

Linux--线程安全的单例模式--自旋锁--0211

1. 线程安全的单例模式 1.1 什么是单例模式某些类, 只应该具有一个对象(实例), 就称之为单例. 1.1.1 懒汉方式实现单例模式以上篇博文的线程池为例 Liunx--线程池的实现--0208 09_Gosolo！的博客-CSDN博客实现懒汉模式首先要先将构造函数私有化，…...

编程日记 2023/5/23 5:30:13

图文解说S参数（进阶篇）

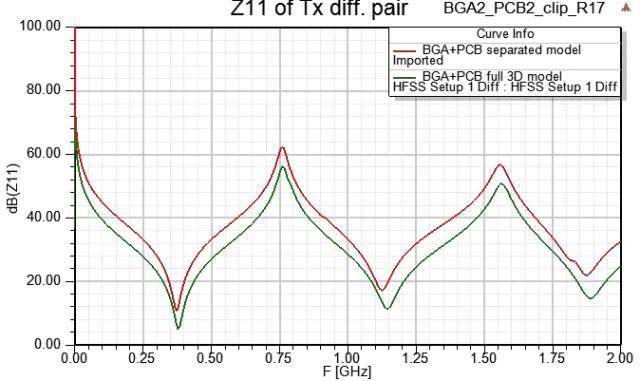
S参数是RF工程师/SI工程师必须掌握的内容，业界已有多位大师写过关于S参数的文章，即便如此，在相关领域打滚多年的人， 可能还是会被一些问题困扰着。你懂S参数吗? 图文解说S参数（基础篇） 请继续往下看...台湾…...

编程日记 2023/5/8 19:27:45

Sentinel源码阅读

基础介绍 Sentinel 的使用可以分为两个部分: 核心库（Java 客户端）：不依赖任何框架/库，能够运行于 Java 8 及以上的版本的运行时环境，同时对 Dubbo / Spring Cloud 等框架也有较好的支持（见主流框架适配&…...

编程日记 2023/5/26 12:26:07

2023年浙江食品安全管理员考试真题题库及答案

百分百题库提供食品安全管理员考试试题、食品安全管理员考试预测题、食品安全管理员考试真题、食品安全管理员证考试题库等，提供在线做题刷题，在线模拟考试，助你考试轻松过关。一、判断题 7.（重点）《餐饮服务食品安全…...

编程日记 2023/5/5 7:08:17

Webstorm 代码没有提示，uniapp 标签报错

问题项目是用脚手架创建的： vue create -p dcloudio/uni-preset-vue my-project 打开之后，添加view标签警告报错的。代码也没有提示，按官方说法：CLI 工程默认带了 uni-app 语法提示和 5App 语法提示。但是我这里就是有问题。…...

编程日记 2023/5/11 8:47:40

MySQL-Innodb引擎事务原理

文章目录1.事务介绍2 事务特性3. 事务的实现原理4 redo log 保证持久性5 undo log 保证原子性6 MVCC 概念6.1 隐藏字段6.2 版本链6.3 ReadView6.3.1readview 版本控制规则7 隔离性实现7.2 隔离性- REPEATABLE READ 可重复读下8 一致性1.事务介绍事务是一组操作的集合&#xf…...

编程日记 2023/5/16 0:16:31

Linux操作系统学习（了解环境变量）

文章目录环境变量初识除了上述介绍的PATH，还有一些常见的环境变量如：查看环境变量方法 ：环境变量的基本概念：本地变量：环境变量初识环境变量解释起来比较抽象，先看示例： #include <stdio.…...

编程日记 2023/5/28 5:56:46

数据分析思维（六）｜循环/闭环思维

循环/闭环思维 1、概念在很多的分析场景下，我们需要按照一套流程反复分析，而不是进行一次性的分析，也就是说这套流程的结果会成为该流程的新一次输入，从而形成一个闭环，此时的分析思维我们称之为循环/闭环思维。常…...

编程日记 2023/5/31 9:59:08

C++：类和对象（下）

文章目录1 再谈构造函数1.1 构造函数体赋值1.2 初始化列表1.3 explicit关键字2 static成员2.1 概念2.2 特性3 友元3.1 友元函数（流插入（<<）及流提取（>>）运算符重载）3.2 友元类4 内部类5 匿名对…...

编程日记 2023/5/3 15:02:34

ASP.NET Core MVC 项目 AOP之IResultFilter和IAsyncResultFilter

目录一：说明二：IActionFilter同步三：IAsyncActionFilter异步一：说明 IResultFilter同步过滤器与IAsyncResultFilter异步过滤器常常被用作于渲染视图或处理结果。 IResultFilter同步过滤器执行顺序： 1：执行控制器中的构造函数，实例化控制器 2：执行具体的Acti…...

编程日记 2023/5/21 0:49:55

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 （1）连接查询（JOIN） 内连接（INNER JOIN）：返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29