Latex数学公式排版
文章目录
- Latex使用
- 最佳方式:读官方文档
- Latex中的字符
- 数学公式排版
- 1.引入宏包:
- 2.公式排版基础
- 3.数学符号
- (1).希腊字母
- (2).指数,上下标,导数
- (3).分式和根式
- (4).关系符
- (5).算符
- (6).巨算符
- (7).箭头
Latex使用
最佳方式:读官方文档
The not so short introduction to latex各种语言版本下载地址
Latex中的字符
-
空格和分段:
- 空格键和Tab 键输入的空白字符视为“空格”。连续的若干个空白字符视
为一个空格。一行开头的空格忽略不计 - 多个空行被视为一个空行。也可以在行末使用 \par 命令分段。
- 空格键和Tab 键输入的空白字符视为“空格”。连续的若干个空白字符视
-
注释: %
-
特殊字符: # $ % & 等等,均需转义
\# \$ \% \& \{ \} \_
\^{} \~{} \textbackslash# $ % & { } _ ^ ~ \
-
标点符号:
- 引号: 中文直接输入,英文
``Please press the `x' key.''“Please press the ‘x’ key.”- 连字号和破折号
daughter-in-law, X-rated\\ pages 13--67\\ yes---or no? % -个数的区别 daughter-in-law, X-rated pages 13–67 yes—or no?- 省略号:
\ldots或\dots
数学公式排版
1.引入宏包:
\usepackage{amsmath}
2.公式排版基础
-
行内公式和行间公式:
- 行内公式由一对$符号包裹
The Pythagorean theorem is $a^2 + b^2 = c^2$.- 行间公式由equation 环境包裹
The Pythagorean theorem is: \begin{equation} a^2 + b^2 = c^2 \label{pythagorean} \end{equation} Equation \eqref{pythagorean} is called `Gougu theorem' in Chinese.

\begin{equation*}
a^2 + b^2 = c^2
\end{equation*}
For short:
\[ a^2 + b^2 = c^2 \]
Or if you like the long one:
\begin{displaymath}
a^2 + b^2 = c^2
\end{displaymath}% 如果需要直接使用不带编号的行间公式,则将公式用命令\[ 和\] 包裹,与之等效的是displaymath 环境

3.数学符号
(1).希腊字母

(2).指数,上下标,导数
Latex中使用 ^ 和 _ 标明上下标.上下标内容需要用花括号{}包裹, 否则上下标只对后面一个符号起作用.
\(p^3_{ij} \qquadm_\mathrm{Knuth}\qquad\sum_{k=1}^{3} k
\) \\[5pt]\(a^x+y \neq a^{x+y}\qquade^{x^2} \neq {e^x}^2
\)
% \(\) 亦可用于行内公式

导数符号 ’ 是一类特殊的上标,可以适当连用表示多阶导数
\(f(x) = x^3 \quad f'(x) = 3x^2
\)\(f''(x) = 6x \quad f^{3}(x) = 6
\)

(3).分式和根式
- 分式使用 \frac{分子}{分母} 来书写; amsmath也提供 \dfrac 和 \tfrac 两种不同的size
In display style:
\[
3/8 \qquad \frac{3}{8}
\qquad \tfrac{3}{8}
\]
In text style:
$1\frac{1}{2}$~hours \qquad
$1\dfrac{1}{2}$~hours

- 根式 使用 \sqrt{…} ; 表示n次方根 \sqrt[n]{…}
(4).关系符

(5).算符

(6).巨算符
行内和行间的显示不同
巨算符的上下标位置可由\limits 和\nolimits 调整,前者令巨算符类似lim 或求和算符,上下标位于上下方;后者令巨算符类似积分号,上下标位于右上方和右下方
In text:
$\sum\limits_{i=1}^n \quad
\int\limits_0^{\frac{\pi}{2}} \quad
\prod\limits_\epsilon $ \\In display:
\[\sum\nolimits_{i=1}^n \quad
\int\limits_0^{\frac{\pi}{2}} \quad
\prod\nolimits_\epsilon \]
\end{document}

(7).箭头

相关文章:

Latex数学公式排版
文章目录 Latex使用最佳方式:读官方文档Latex中的字符数学公式排版1.引入宏包:2.公式排版基础3.数学符号(1).希腊字母(2).指数,上下标,导数(3).分式和根式(4).关系符(5).算符(6).巨算符(7).箭头 Latex使用 最佳方式:读官方文档 The not so short intro…...

【Linux】-关于Linux的指令(上)
作者:小树苗渴望变成参天大树 作者宣言:认真写好每一篇博客 作者gitee:gitee 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧! TOC 前言 今天我们来讲关于Linux的基本指令,博主讲的指令会对应着Windows…...

【论文写作】引言写作的四个重要的语言点之时态!!!
在本篇文章当中,我们将着重介绍四个重要的写作语言要点之一的时态,其他语言点如下: 1. 时态 2. 标志性的衔接词 3. 主动、被动语态 4. 段落 1. 简单现在时和现在进行时 时态主要有现在时和现在进行时,看以下两个句子 I live in…...
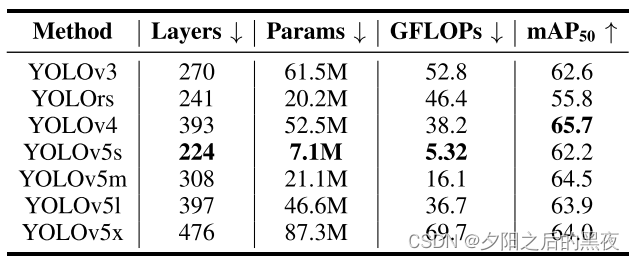
Super Yolo论文翻译
论文:SuperYOLO: Super Resolution Assisted Object Detection in Multimodal Remote Sensing Imagery【IEEE】 论文地址: IEEE Xplore Full-Text PDF:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp&arnumber10075555项目地址:icey…...
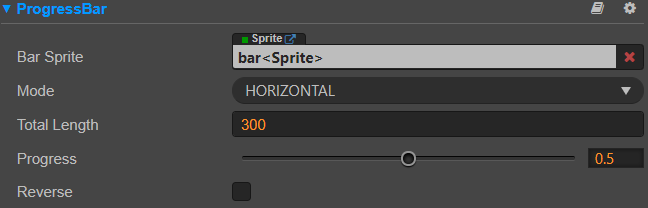
【CocosCreator入门】CocosCreator组件 | ProgressBar(进度条)组件
Cocos Creator 是一款流行的游戏开发引擎,具有丰富的组件和工具,其中的ProgressBar组件是一种用于实现进度条效果的重要组件。它可以让我们在游戏中展示各种进度条效果,例如加载进度条、血条等。 目录 一、组件介绍 二、组件属性 三、脚本…...
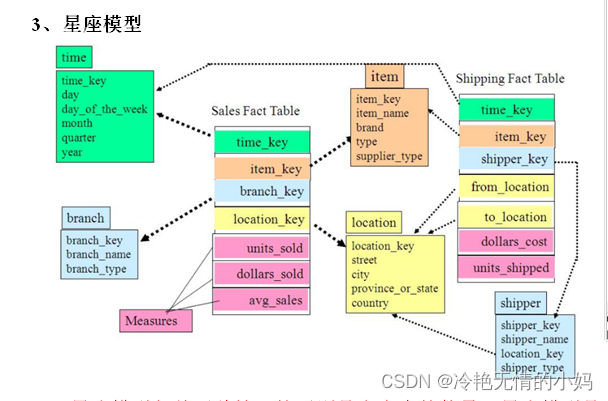
大数据数仓维度建模
目录 维度建模分为三种: 1、星型模型: 2、雪花模型: 3、星座模型: 模型的选择: 维度表和事实表: 维度表: 维度表特性 : 事实表: 事实表特性: 事务型…...

ESP32设备驱动-BH1745NUC 亮度和颜色传感器驱动
BH1745NUC 亮度和颜色传感器驱动 文章目录 BH1745NUC 亮度和颜色传感器驱动2、硬件准备3、软件准备4、驱动实现BH1745NUC 是具有 IC 总线接口的数字颜色传感器 IC。 该 IC 感应红光、绿光和蓝光 (RGB) 并将它们转换为数字值。 高灵敏度、宽动态范围和出色的 Ircut 特性使该 IC …...

通达信VCP形态选股公式,憋了好几天才写出来
VCP形态的英文”Volatility Contraction Pattern”的缩写,意思是“波动收缩形态”。VCP形态是全美交易冠军马克米勒维尼的核心交易模式之一,在其著作《股票魔法师》中有详细介绍。 马克米勒维尼把VCP形态比喻为湿毛巾,拧过一次后仍含水&…...

vue 知识储备
vue2 和 vue3 的区别 模块拆分:vue3采用 compnent API 更注重模块上的拆分,而vue2中则需要使用完整的vuejs,无法使用单独的模块重写API:vue2组件方法挂载到实例中未使用也会被打包,vue3通过 tree-shaking机制,实现按需引入,减少用户打包后体积数据双向绑定:vue2使用 Ob…...
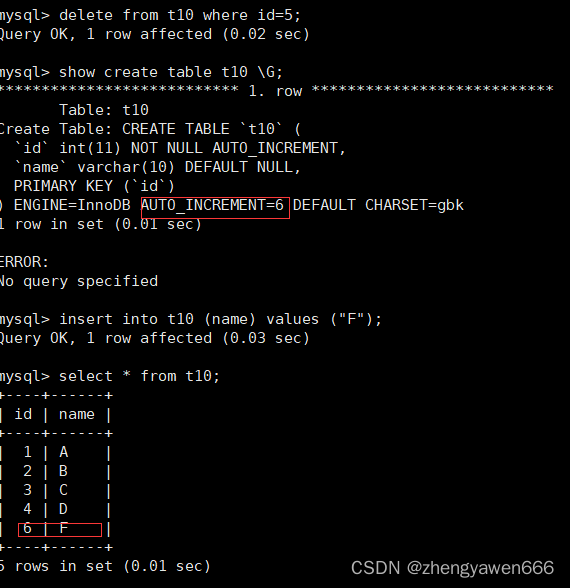
MySQL表的增删查改
目录 一 插入 1 基本语法 ①全列插入 ②指定列插入 ③多条记录插入 ④冲突更新 二 查询 查询全部数据 指定列查询 显示 拼接 取别名 去重查找 where 逻辑运算符和比较运算符 结果排序 Limit group by 分组 聚合函数 对于count 对于sum 对于group by 相关的语…...

详解C语言string.h中常用的14个库函数(三)
本篇博客继续讲解C语言string.h头文件中的库函数。本篇博客计划讲解3个函数,分别是:strstr, strtok, strerror。其中strstr函数我会用一种最简单的方式模拟实现。 strstr char * strstr ( const char * str1, const char * str2 );strstr可以在str1中查…...

无人机视频与GIS融合三维实景怎么实现?
无人机视频与GIS融合三维实景怎么实现?无人机三维GIS作为一项新兴的测绘重要手段,具有续航时间长、成本低、机动灵活等优点,为城市的规划建设带来极大便利。 那么此项技术有什么样的特点呢?下面智汇云舟就带大家一起来了解一下。 三维是将采集以及经运…...

瞬间让你效率提高一倍的高效学习方法
方法不对,努力白费;方法对了,事半功倍!在学习的过程中我们会遇到各种困难与阻碍,如何发现并优化自己的学习方法就变得尤为重要。高效学习方法是指通过科学的、有效的方法来提高学习效率,实现更好的学习成果…...

442. 数组中重复的数据|||41. 缺失的第一个正数|||485. 最大连续 1 的个数
442. 数组中重复的数据 题目 给你一个长度为 n 的整数数组 nums ,其中 nums 的所有整数都在范围 [1, n] 内,且每个整数出现 一次 或 两次 。请你找出所有出现 两次 的整数,并以数组形式返回。 你必须设计并实现一个时间复杂度为 O(n) 且仅…...
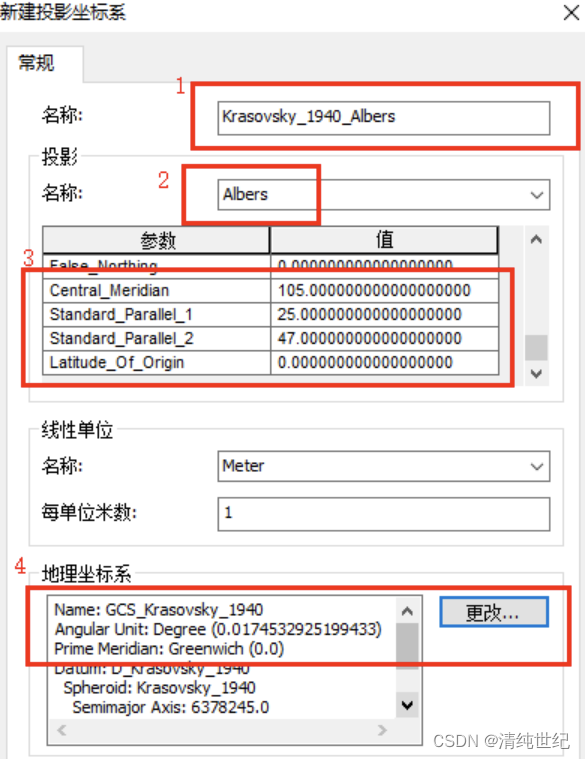
中国地图标准坐标和投影参数
目录 一、地理坐标 二、投影坐标 三、ArcGIS投影变换 四、说明 一、地理坐标 GCS_Krasovsky_1940(克拉索夫斯基_1940椭球体) 具体参数如下图: 每个国家或地区都有各自的基准面,我们通常所说的北京54坐标系、西安80坐标系实际上…...

CNN中卷积层、池化的计算公式
卷积计算公式 1、卷积层输入特征图(input feature map)的尺寸为:(batch_size,Channel,H,W) H(input)表示输入特征图的高 W(input)表示输入特征图的宽 C(input)表示输入特征图的通道数(如果是第一个卷积层则是输入图像的通道数,如果是中间…...

基类派生类多态虚函数?
通常在层次关系的根部有一个基类,其他类则直接或间接的从基类继承而来,这些继承得到的类称为派生类。基类负责定义在层次关系中所有类共同拥有的成员,而每个派生类定义各自特有的成员。 成员函数与继承派生类可以继承其基类的成员, 然而有时…...

像素是什么
像素分为设备像素和设备无关像素。 下面说说来龙去脉。 一、显示器 显示图像的电子设备。 (一)显示器种类 1.LCD LCD(Liquid crystal display),是液体晶体显示,也就是液晶显示器,LCD具有功耗低…...

NAT转换
目录标题 NAT:网络地址转换(cisco篇)一对一(静态)一对多(动态)多对多(动、静均可)端口映射(静态) nat:网络地址转换(华为篇࿰…...

设计模式:创建者模式 - 单例模式
文章目录 1.介绍2.单例模式的结构3.单例模式的实现(饿汉、懒汉)饿汉式-方式1(静态变量方式)饿汉式-方式2(静态代码块方式)懒汉式-方式1(线程不安全)懒汉式-方式2(线程安全…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
