大数据数仓维度建模
目录
维度建模分为三种:
1、星型模型:
2、雪花模型:
3、星座模型:
模型的选择:
维度表和事实表:
维度表:
维度表特性 :
事实表:
事实表特性:
事务型事实表:
周期型快照事实表:
累积型快照事实表:
维度建模分为三种:
1、星型模型:
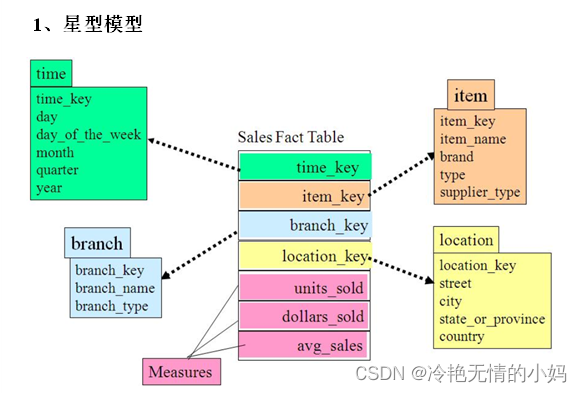
雪花模型与星座模型的区别主要在于维度的层级,标准的星型模型只有一层,而雪花模型可能会涉及多级。
2、雪花模型:
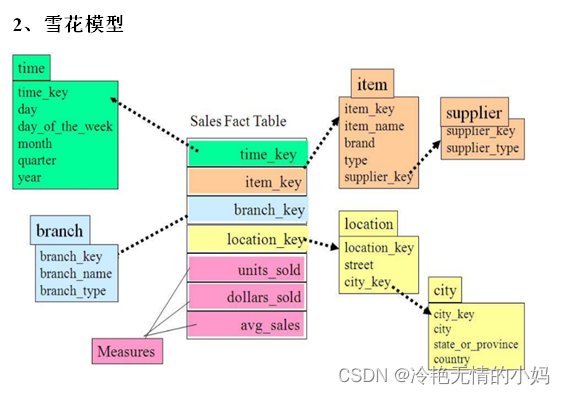
雪花模型,比较靠近3NF,但是无法完全遵守,因为遵循3NF的性能成本太高。
3、星座模型:
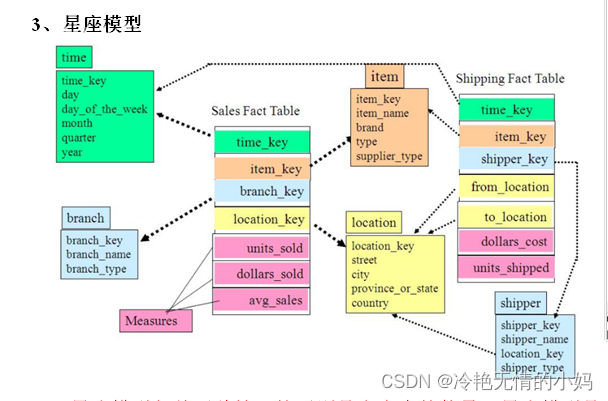
星座模型与前面两种情况的区别是事实表的数量,星座模型是基于多个事实表。
模型的选择:
首先就是星座不星座只跟数据和需求有关系,跟设计没有关系,不用选择。
星型还是雪花,取决于性能优先,还是灵活更优先。
通过市场调研中,不会绝对的选择一种,根据情况灵活组合,甚至并存(一层维度和多层维度都是存在的)。但是从整体来看,星型模型用维度比较少。尤其是Hadoop体系,减少Join就是减少Shuffle,性能差距很大。(关系型数据可以依靠强大的主建索引)。
维度表和事实表:
维度表:
一般是对事实的描述信息。每一张维表对应现实世界中的一个对象或者概念。 例如:用户、商品、日期、地区等。
维度表特性 :
- 维表的范围很宽(具有多个属性、列比较多)
- 跟事实表相比,行数相对较小:通常< 10万条
- 内容相对固定:编码表
事实表:
每行数据代表一个业务事件(下单、支付、退款、评价等)
事实表特性:
- 非常的大
- 内容相对的窄:列数较少(主要是外键id和度量值)
- 经常发生变化,每天会新增加很多。
事务型事实表:
以每个事务或事件为单位,例如一笔支付记录,作为事实表里的一行数据。一旦事务被提交,事实表数据被插入,数据就不再进行更改,其更新方式为增量更新。
周期型快照事实表:
周期型快照事实表中不会保留所有数据,只保留固定时间间隔的数据,例如每天或者每月的销售额,或每月的账户余额等。
例如购物车,有加减商品,随时都有可能变化,但是我们更关心每天结束时这里面有多少商品,方便我们后期统计分析。
累积型快照事实表:
累计快照事实表用于跟踪业务事实的变化。例如,数据仓库中可能需要累积或者存储订单从下订单开始,到订单商品被打包、运输、和签收的各个业务阶段的时间点数据来跟踪订单声明周期的进展情况。当这个业务过程进行时,事实表的记录也要不断更新。
相关文章:

大数据数仓维度建模
目录 维度建模分为三种: 1、星型模型: 2、雪花模型: 3、星座模型: 模型的选择: 维度表和事实表: 维度表: 维度表特性 : 事实表: 事实表特性: 事务型…...

ESP32设备驱动-BH1745NUC 亮度和颜色传感器驱动
BH1745NUC 亮度和颜色传感器驱动 文章目录 BH1745NUC 亮度和颜色传感器驱动2、硬件准备3、软件准备4、驱动实现BH1745NUC 是具有 IC 总线接口的数字颜色传感器 IC。 该 IC 感应红光、绿光和蓝光 (RGB) 并将它们转换为数字值。 高灵敏度、宽动态范围和出色的 Ircut 特性使该 IC …...

通达信VCP形态选股公式,憋了好几天才写出来
VCP形态的英文”Volatility Contraction Pattern”的缩写,意思是“波动收缩形态”。VCP形态是全美交易冠军马克米勒维尼的核心交易模式之一,在其著作《股票魔法师》中有详细介绍。 马克米勒维尼把VCP形态比喻为湿毛巾,拧过一次后仍含水&…...

vue 知识储备
vue2 和 vue3 的区别 模块拆分:vue3采用 compnent API 更注重模块上的拆分,而vue2中则需要使用完整的vuejs,无法使用单独的模块重写API:vue2组件方法挂载到实例中未使用也会被打包,vue3通过 tree-shaking机制,实现按需引入,减少用户打包后体积数据双向绑定:vue2使用 Ob…...
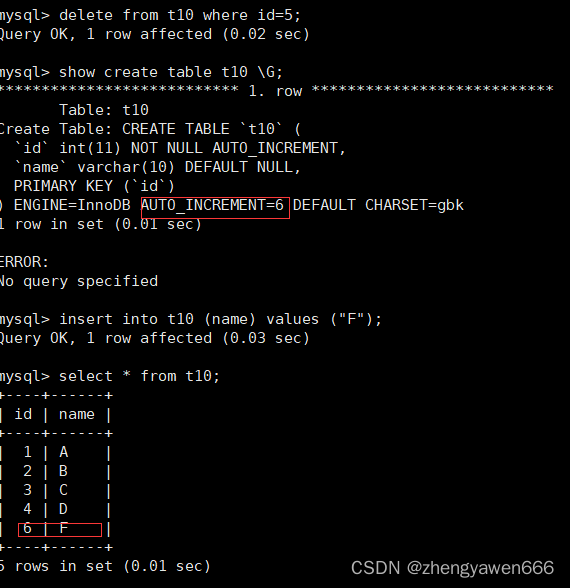
MySQL表的增删查改
目录 一 插入 1 基本语法 ①全列插入 ②指定列插入 ③多条记录插入 ④冲突更新 二 查询 查询全部数据 指定列查询 显示 拼接 取别名 去重查找 where 逻辑运算符和比较运算符 结果排序 Limit group by 分组 聚合函数 对于count 对于sum 对于group by 相关的语…...

详解C语言string.h中常用的14个库函数(三)
本篇博客继续讲解C语言string.h头文件中的库函数。本篇博客计划讲解3个函数,分别是:strstr, strtok, strerror。其中strstr函数我会用一种最简单的方式模拟实现。 strstr char * strstr ( const char * str1, const char * str2 );strstr可以在str1中查…...

无人机视频与GIS融合三维实景怎么实现?
无人机视频与GIS融合三维实景怎么实现?无人机三维GIS作为一项新兴的测绘重要手段,具有续航时间长、成本低、机动灵活等优点,为城市的规划建设带来极大便利。 那么此项技术有什么样的特点呢?下面智汇云舟就带大家一起来了解一下。 三维是将采集以及经运…...

瞬间让你效率提高一倍的高效学习方法
方法不对,努力白费;方法对了,事半功倍!在学习的过程中我们会遇到各种困难与阻碍,如何发现并优化自己的学习方法就变得尤为重要。高效学习方法是指通过科学的、有效的方法来提高学习效率,实现更好的学习成果…...

442. 数组中重复的数据|||41. 缺失的第一个正数|||485. 最大连续 1 的个数
442. 数组中重复的数据 题目 给你一个长度为 n 的整数数组 nums ,其中 nums 的所有整数都在范围 [1, n] 内,且每个整数出现 一次 或 两次 。请你找出所有出现 两次 的整数,并以数组形式返回。 你必须设计并实现一个时间复杂度为 O(n) 且仅…...
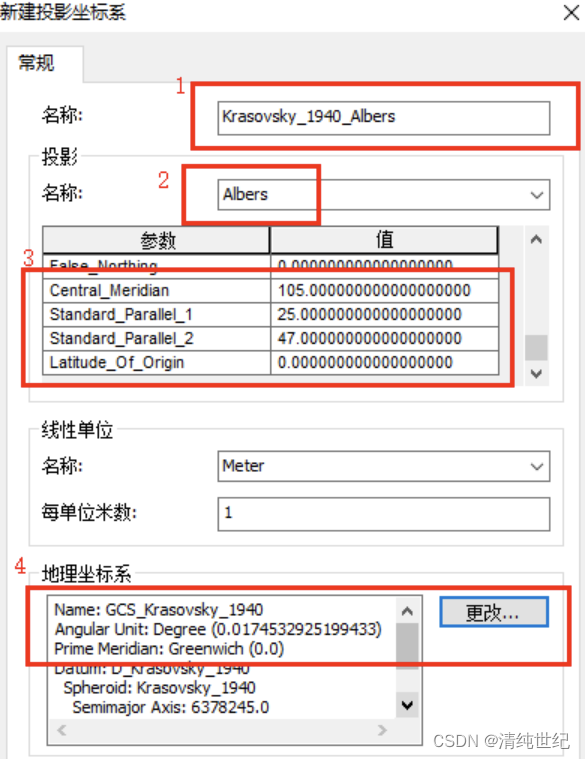
中国地图标准坐标和投影参数
目录 一、地理坐标 二、投影坐标 三、ArcGIS投影变换 四、说明 一、地理坐标 GCS_Krasovsky_1940(克拉索夫斯基_1940椭球体) 具体参数如下图: 每个国家或地区都有各自的基准面,我们通常所说的北京54坐标系、西安80坐标系实际上…...

CNN中卷积层、池化的计算公式
卷积计算公式 1、卷积层输入特征图(input feature map)的尺寸为:(batch_size,Channel,H,W) H(input)表示输入特征图的高 W(input)表示输入特征图的宽 C(input)表示输入特征图的通道数(如果是第一个卷积层则是输入图像的通道数,如果是中间…...

基类派生类多态虚函数?
通常在层次关系的根部有一个基类,其他类则直接或间接的从基类继承而来,这些继承得到的类称为派生类。基类负责定义在层次关系中所有类共同拥有的成员,而每个派生类定义各自特有的成员。 成员函数与继承派生类可以继承其基类的成员, 然而有时…...

像素是什么
像素分为设备像素和设备无关像素。 下面说说来龙去脉。 一、显示器 显示图像的电子设备。 (一)显示器种类 1.LCD LCD(Liquid crystal display),是液体晶体显示,也就是液晶显示器,LCD具有功耗低…...

NAT转换
目录标题 NAT:网络地址转换(cisco篇)一对一(静态)一对多(动态)多对多(动、静均可)端口映射(静态) nat:网络地址转换(华为篇࿰…...

设计模式:创建者模式 - 单例模式
文章目录 1.介绍2.单例模式的结构3.单例模式的实现(饿汉、懒汉)饿汉式-方式1(静态变量方式)饿汉式-方式2(静态代码块方式)懒汉式-方式1(线程不安全)懒汉式-方式2(线程安全…...

C++语言亚马逊国际获取AMAZON商品详情 API接口(
跨境电子商务是一种全新的互联网电商模式,运用电子化方式促成线上跨境交易,利用跨境物流运送商品,有利于打破传统的贸易格局,成为新的经济增长点。对我国来说,跨境电商平台正用一种全新的力量改变我国产业链的结构&…...
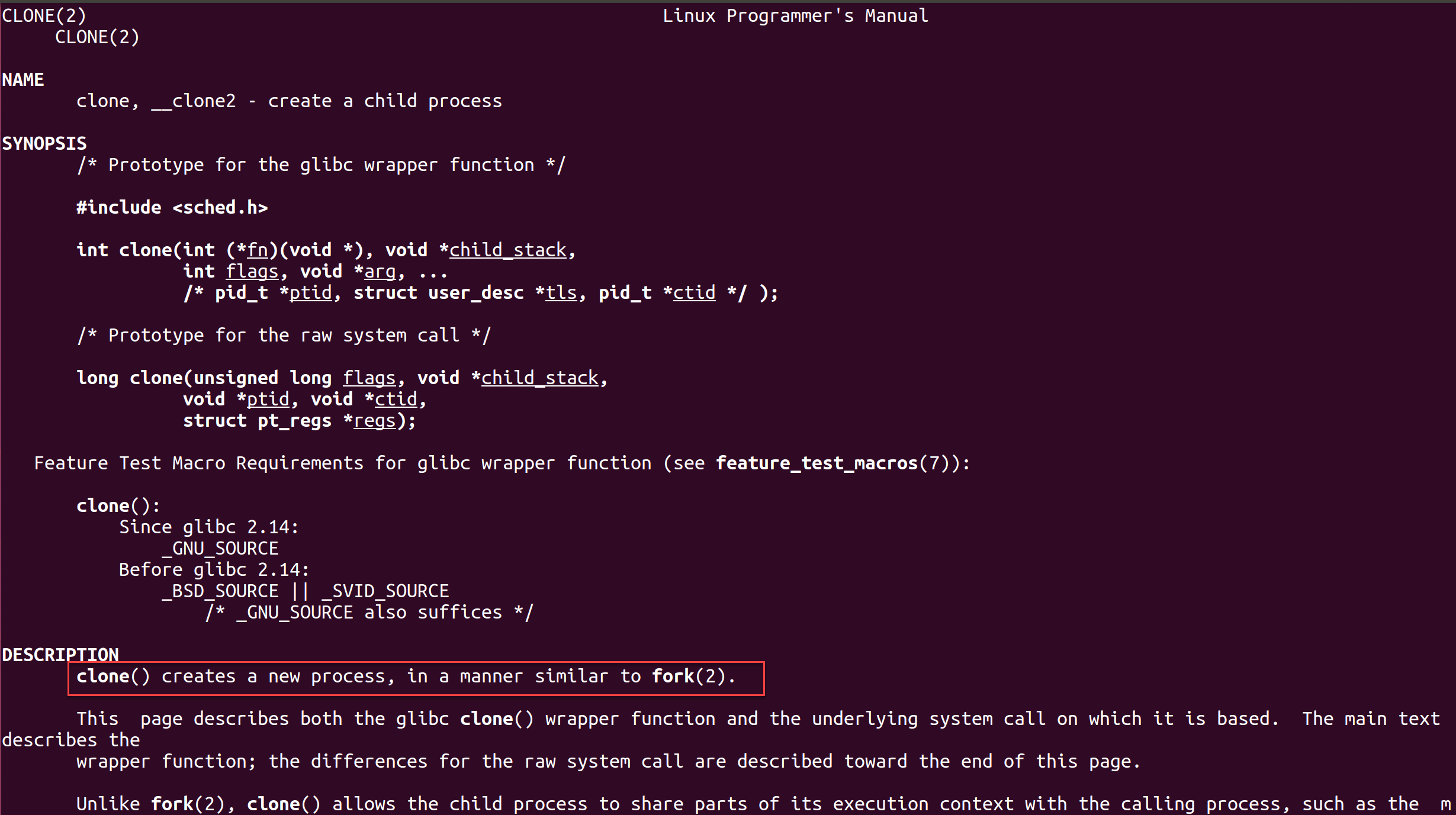
在程序里面执行system(“cd /某个目录“),为什么路径切换不成功?
粉丝提问: 彭老师,问下,在程序里面执行system(“cd /某个目录”),这样会切换不成功,为啥呢 实例代码: 粉丝的疑惑是明明第10行执行了cd /media操作, 为什么12行执行的pwd > test2.txt 结…...

c++ 对类与对象的基础框架+完整思维导图+基本练习题+深入细节+通俗易懂建议收藏
绪论 上一章,我们将c入门的基础知识进行了学习,本章其实才算真正的跨入到c开始可能比较难,但只有我们唯有不断的前进,才能斩断荆棘越过人生的坎坷! 话不多说安全带系好,发车啦(建议电脑观看&…...
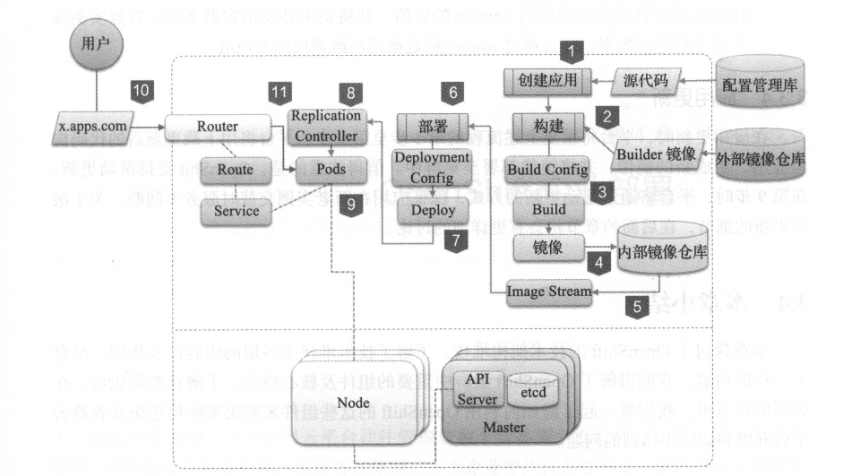
关于Open Shift(OKD) 中应用管理部署的一些笔记
写在前面 因为参加考试,会陆续分享一些 OpenShift 的笔记博文内容为介绍 openshift 不同的创建应用的方式,包括: 基于 IS 创建应用基于镜像创建应用基于源码和 image 创建应用基于源码和 IS 创建应用基于模板创建应用 学习环境为 openshift v…...
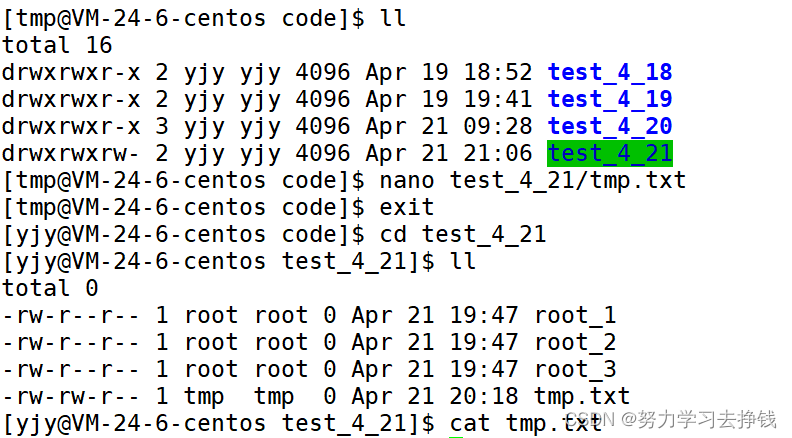
【linux】对于权限的理解
权限 Linux权限的概念用户之间的切换 Linux权限管理文件权限操作文件的人Linux文件默认权限的设置权限掩码 所属组/其他删除拥有者创建的文件文件拥有者、所属组的修改修改文件拥有者修改文件所属组一次性修改拥有者和所属组 目录的执行权限 Linux权限的概念 首先,…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
