Delaunay三角网生成算法
目录
- 一、分而治之算法
- 二、三角网生长算法
- 三、逐点插入算法
- 四、约束Delaunay三角网
- 1、方法一
- 1、原始点云
- 2、构网结果
- 1、方法二
- 1、原始点云
- 2、普通Delaunay
- 3、约束Delaunay
Delaunay三角剖分分为直接三角剖分和间接三角剖分。间接三角剖分首先计算为Voronoi图,然后由Voronoi图产生Delaunay三角网。这种方法的算法复杂、内存开销大、效率低,现今很少使用。直接Delaunay三角剖分是利用离散点按照空外接圆或者最大最小内角性质,直接生成Delaunay三角网,是目前基于离散点三角剖分的主流算法。
Delaunay三角剖分分成三类:分而治之算法、三角网增长算法和逐点插入算法。
一、分而治之算法
分而治之算法最早是1975年由Shamos和Hoey提出的,Lewis和Rovinson在1978年利用该方法进行了三角网的剖分,随后Lee和Schachter、Dwyer等对他们的算法进行了改进和优化。
分而治之算法的思路是将复杂问题简单化,首先将数据点分割成包含少量点的子集,如一个子集中包括三个、四个点,然后每个子集进行三角剖分,并用局部优化算法(LOP)进行优化,保证三角剖分为Delaunay三角网,最后是对每个子集的三角剖分进行合并,形成最终的整体三角网。不同的实现方法可有不同的点集划分方法、子网生成方法及合并方法。Lee和Schachter提出了分而治之的经典算法,其基本步骤如下:
- 把点集 V V V以横坐标为主,纵坐标为辅按升序排序,即数据点之间满足条件: ( x i , y i ) < = ( x i + 1 , y i + 1 ) (x_i,y_i)<=(x_{i+1},y_{i+1}) (xi,yi)<=(xi+1,yi+1);
- 把点集 V V V分为近似相等的两个子集 V L V_L VL和 V R V_R VR;
- 在 V L V_L VL和 V R V_R VR中生成三角网;
- 使用局部优化算法,使之成为Delaunay三角网;
- 找出连接 V L V_L VL和 V R V_R VR中两个凸壳的底线和顶线;
- 由底线至顶线合并 V L V_L VL和 V R V_R VR中两个三角网;
- 结束。
该算法的时间复杂度为 ( N l o g N ) (NlogN) (NlogN),其中 N N N为数据点数,因此该算法执行时间效率高,但在 V L V_L VL和 V R V_R VR中生成三角网时,采用了递归运算,需占用较大的系统内存。
二、三角网生长算法
三角网生长算法最早由Green和Sibson在V图中实现,稍后Brassel和Teif也发表了类似的算法。分为收缩生长算法和扩张生长算法,收缩生长算法是先生成凸壳,并以凸壳为源头,逐步缩小以形成整个三角网。收缩生长算法与数据点的分布密度有关,实际情况比较复杂。扩张生成算法与收缩算法过程刚好相反,算法是从一个三角形开始向外层扩展,最终形成覆盖整个区域的三角网,是常用的三角网生长算法。
扩张生长算法的思想是先找出点集中最近两点连接成一条边,按照Delaunay三角网构成原则找出第三点,将这三点连接成初始三角形,再以该三角形的每一条边为基线扩展连接相邻离散点,组成新三角形,初始三角形的三边处理之后,继续以新三角形的边连接其他离散点,直到所有的离散点均包含在三角网中。该算法的基本步骤:
- 在区域内所有离散点任取一点作为初始三角形的第一个顶点;
- 找距离第一个顶点最近的点,作为初始三角形的第二个顶点,两点相连生成初始基线;
- 找出距离初始基线中点最近且不和已有两点在一条直线上的点作为初始三角形的第三个顶点,三点连接成三角形,即为初始三角形;
- 三角形的两条新边作为新的基线;
- 重复步骤3、4直到所有基线处理完毕。
该算法的时间复杂度在一般情况下为 O ( N 3 / 2 ) O(N^{3/2}) O(N3/2),最坏情况下达到 O ( N 2 ) O(N^2) O(N2)。因此该算法的时间效率低,优点是占用内存空间较小。在该算法的基础上有许多的改进算法,其改进点主要集中在“第三点”的搜索和三角形重复的判断上。
三、逐点插入算法
逐点插入算法的思想最早由Lawson(1977)提出,随后Lee和Schachter(1980)、Bowyer(1981)、Watson(1981)、Tsai(1993)等先后对其进行改进,是一种动态的构网方式。
逐点插入算法的思路是将未处理的点加入到己经存在的Delaunay三角网中,然后判断点所在的三角形,如果点在三角形内,连接点与三角形的各顶点,利用三角剖分准则,找出影响区域,删除影响区域中的边,对影响区域利用三角剖分准则重新构网,直到区域中所有的点都加入到三角网中。该算法的基本步骤如下:
- 首先定义一个包含所有数据点的初始多边形,即包含所有数据点的凸闭包;
- 在凸闭包中构建初始Delaunay三角网;
- 从内部数据点中取出一点加入到三角网中;
- 搜寻包含该点的三角形,将该点与此三角形的三个顶点相连,形成三个三角形;
- 利用Delaunay三角网的剖分准则,找出影响区域,从里到外更新所有生成的三角形;
- 重复步骤3、4、5直到处理完点集中所有点。
该算法一般情况下时间复杂度为 O ( N 3 / 2 ) O(N^{3/2}) O(N3/2),最坏情况下达到 O ( N 2 ) O(N^2) O(N2)。该算法的时间效率低,优点是算法思路较简单,占用内存空间较小,空间性能较好。
通常,分而治之算法的效率是最高的,但是当数据量比较大,分块比较多时,块之间的合并算法复杂,且花时也多,并且递归执行,内存消耗大;三角网生长算法和逐点插入法的执行效率差不多,但是在构网的过程中逐点插入法能保持较好的空间特性。
四、约束Delaunay三角网
1、方法一
1、原始点云

2、构网结果

1、方法二
1、原始点云

2、普通Delaunay

3、约束Delaunay

相关文章:

Delaunay三角网生成算法
目录 一、分而治之算法二、三角网生长算法三、逐点插入算法四、约束Delaunay三角网1、方法一1、原始点云2、构网结果 1、方法二1、原始点云2、普通Delaunay3、约束Delaunay Delaunay三角剖分分为直接三角剖分和间接三角剖分。间接三角剖分首先计算为Voronoi图,然后由Voronoi图产…...

hashcode是什么?有什么作用?
文章目录 (1)hashcode()方法的作用(2)equals和hashcode的关系(3)百度百科(4)小白解释 Java中Object有一个方法: public native int hashcode(); (1࿰…...

【人体姿态估计】(一)原理介绍
【人体姿态估计】(一)原理介绍 一、背景 人体姿态估计本质上是一个关键点检测的项目; 关键点检测在生活中的应用十分广泛,包括人脸识别、手势识别,而人体姿态估计则是对身体的关键点进行检测; 本文将介…...
特性)
一种新的流:为 Java 加入生成器(Generator)特性
作者:文镭(依来) 前言 这篇文章不是工具推荐,也不是应用案例分享。其主题思想,是介绍一种全新的设计模式。它既拥有抽象的数学美感,仅仅从一个简单接口出发,就能推演出庞大的特性集合,引出许多全新概念。…...

《数据结构C++版》实验一:线性表的顺序存储结构
实验目的 1、实现线性表的顺序存储结构 2、熟悉C++程序的基本结构,掌握程序中的头文件、实现文件和主文件之间的相互关系及各自的作用 3、熟悉顺序表的基本操作方式,掌握顺序表相关操作的具体实现 实验内容 对顺序存储的线性表进行一些基本操作。主要包括: (1)插入:操作…...
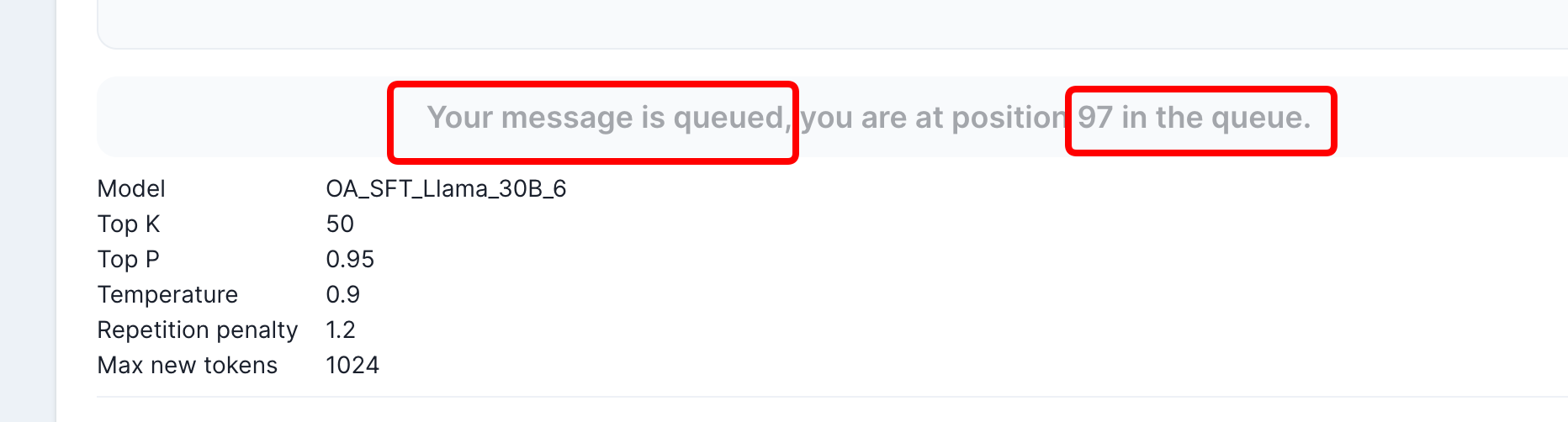
ChatGPT的开源平替,终于来了!
最近这段时间,一个号称全球最大ChatGPT开源平替项目Open Assistant引起了大家的注意。 这不最近还登上了GitHub的Trending热榜。 https://github.com/LAION-AI/Open-Assistant 根据官方的介绍,Open Assistant也是一个对话式的大型语言模型项目ÿ…...

Redis基础
Redis6 1. NoSQL数据库简介 1.1 技术发展 技术的分类 1、解决功能性的问题:Java、Jsp、RDBMS、Tomcat、HTML、Linux、JDBC、SVN。 2、解决扩展性的问题:Struts、Spring、SpringMVC、Hibernate、Mybatis。 3、解决性能的问题:NoSQL、Jav…...

为什么重视安全的公司都在用SSL安全证书?
我们今天来讲一讲为什么重视安全的公司都在用SSL证书 SSL证书是什么? SSL安全证书是由权威认证机构颁发的,是CA机构将公钥和相关信息写入一个文件,CA机构用他们的私钥对我们的公钥和相关信息进行签名后,将签名信息也写入这个文件…...
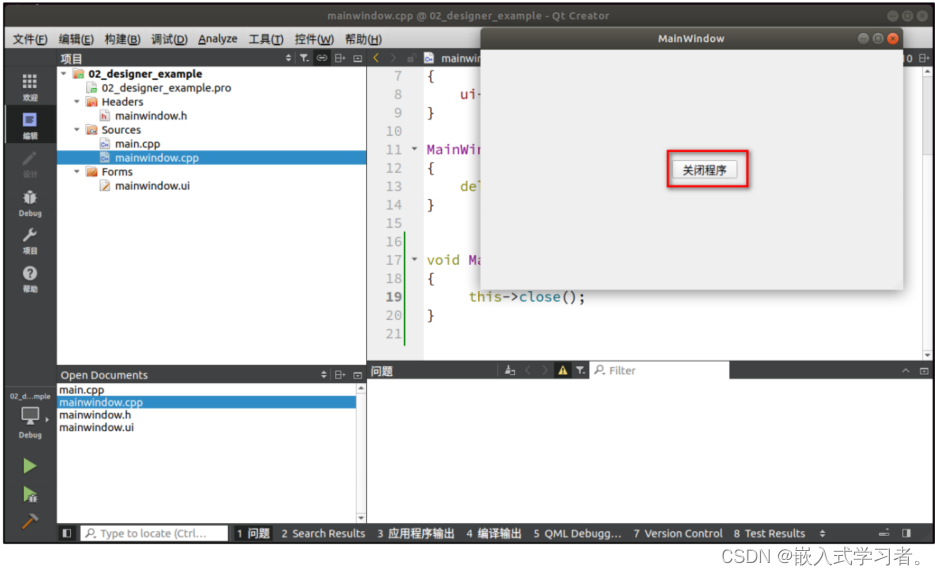
嵌入式QT (使用 Qt Designer 开发)
一、使用 UI 设计器开发程序 1.1、 在 UI 文件添加一个按钮 1.2、在 UI 文件里连接信号与槽 所谓信号即是一个对象发出的信号,槽即是当这个对象发出这个信号时,对应连接的槽就发被执行或者触发。 UI 设计器里信号与槽的连接方法一: 在主窗…...

每日一个小技巧:今天告诉你拍照识别文字的软件有哪些
在现代社会里,手机已经成为了人们生活中必不可少的工具。它的功能众多,比如通讯、上网、拍照以及导航等,为我们的生活带来了许多便利。除此之外,手机还能帮助我们解决一些实际的问题,例如,当你需要识别图片…...

多版本VersionARXDBG
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、一级标题二级标题三级标题四级标题五级标题六级标题总结前言 提示:这里可以添加本文要记录的大概内容: VersionARXDBG,多版本,2023.4.22-4.23两天时间,分别研究了在多版本编译ARXDB…...

# 生成器
生成器 生成器是什么? 生成器(generator)是一种用来生成数据的对象。它们是普通函数的一种特殊形式,可以用来控制数据的生成过程。 生成器有什么优势? 使用生成器的优势在于它们可以在生成数据的同时控制数据的生成过程…...
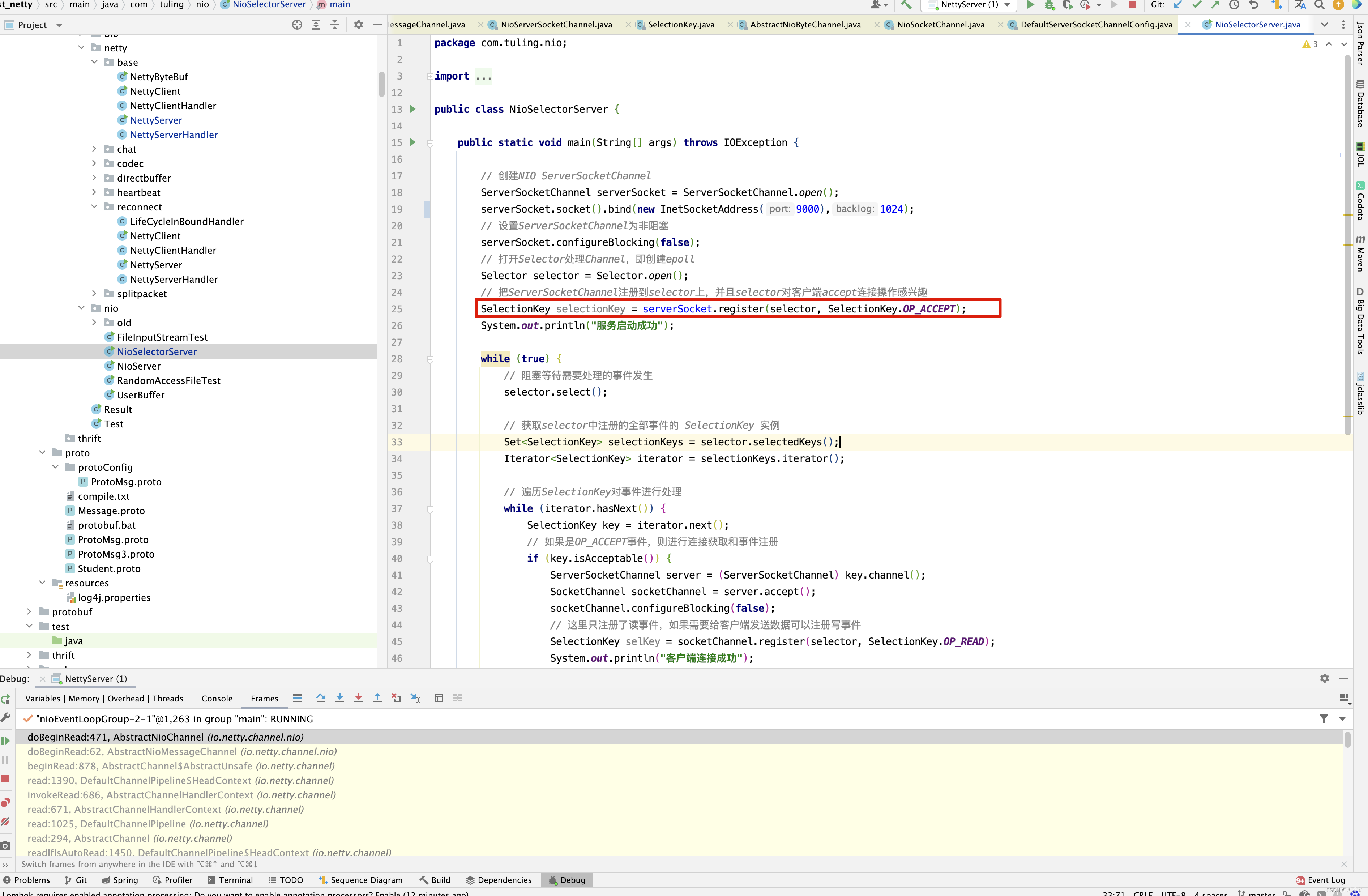
Netty 源码解析(上)
序 Netty的影响力以及使用场景就不用多说了, 去年10月份后,就着手研究Netty源码,之前研究过Spring源码,MyBatis源码,java.util.concurrent源码,tomcat源码,发现一个特点,之前的源码都…...
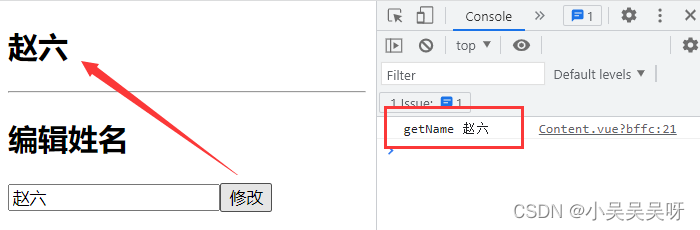
Vue 消息订阅与发布
消息订阅与发布,也可以实现任意组件之间的通信。 订阅者:就相当于是我们,用于接收数据。 发布者:就相当于是媒体,用于传递数据。 安装消息订阅与发布插件: 在原生 JS 中 不太容易实现消息订阅与发布&…...

如何在你的云服务器/云主机上更新并使用最新版本的python(python3.11)
更新并使用最新版本的python3.11 第一步,登录云服务器,并更新系统包 打开您的终端(Terminal)或使用任意SSH客户端,输入如下命令来登录云主机: ssh 用户名IP地址 在输入密码后,您将成功登录到云…...
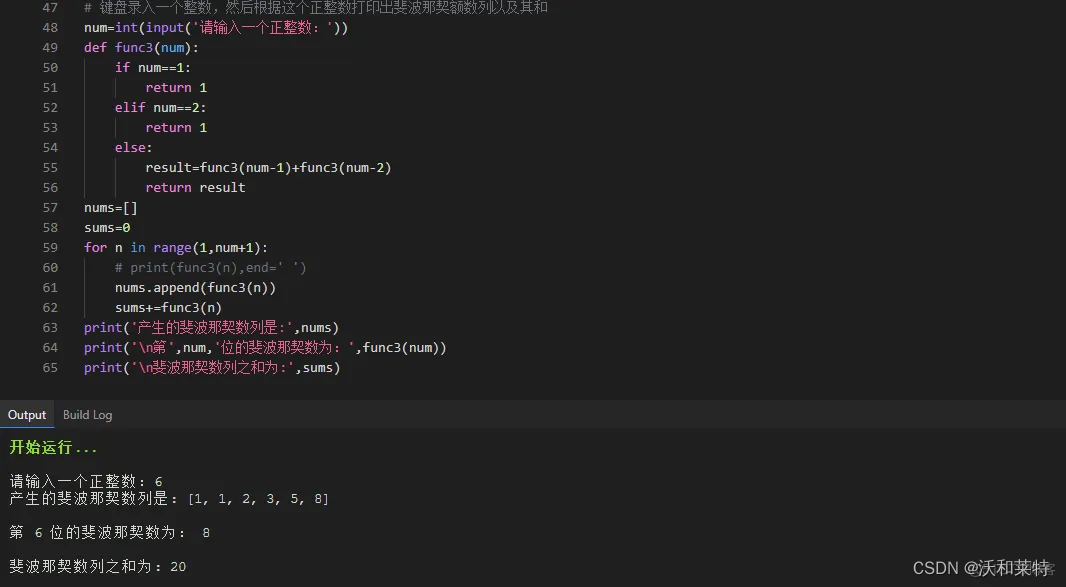
python学习——【第八弹】
前言 上篇文章 python学习——【第七弹】学习了python中的可变序列集合,自此python中的序列的学习就完成啦,这篇文章开始学习python中的函数。 函数 在学习其他编程语言的时候我们就了解过函数:函数就是执行特定任何以完成特定功能的一段代…...
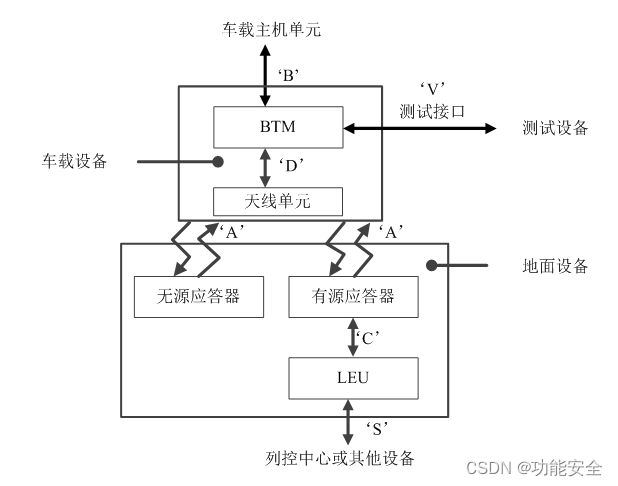
铁路应答器传输系统介绍
应答器传输系统 应答器传输系统是安全点式信息传输系统,通过应答器实现地面设备向车载设备传输信息。 应答器可根据应用需求向车载设备传输固定的(通过无源应答器)或可变的(通过有源应答器)上行链路数据。 当天线单…...
)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK直接实现Mono16位深度的图像保存(C#)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK直接实现Mono16位深度的图像保存(C#) Baumer工业相机Baumer工业相机保存位深度12/16位图像的技术背景代码案例分享1:引用合适的类文件2:通过BGAPI SDK直接保存Mono12/16图像3…...
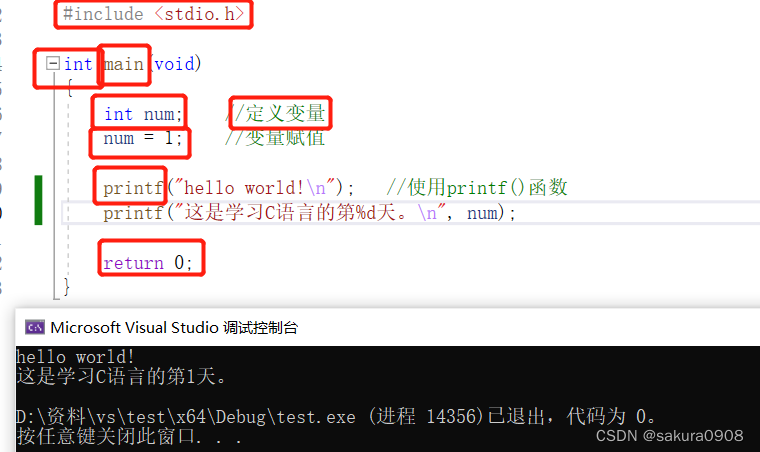
C语言入门篇——介绍篇
目录 1、什么是C语言 1、C语言的优点 3、语言标准 4、使用C语言的步骤 5、第一个C语言程序 6、关键字 1、什么是C语言 1972年,贝尔实验室的丹尼斯里奇和肯汤普逊在开发UNIX操作系统时设计了C语言,C语言是在B语言的基础上进行设计。C语言设计的初衷…...

Latex数学公式排版
文章目录 Latex使用最佳方式:读官方文档Latex中的字符数学公式排版1.引入宏包:2.公式排版基础3.数学符号(1).希腊字母(2).指数,上下标,导数(3).分式和根式(4).关系符(5).算符(6).巨算符(7).箭头 Latex使用 最佳方式:读官方文档 The not so short intro…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
