算法设计与分析(屈婉玲)视频笔记day2
序列求和的方法
数列求和公式
等差、等比数列与调和级数
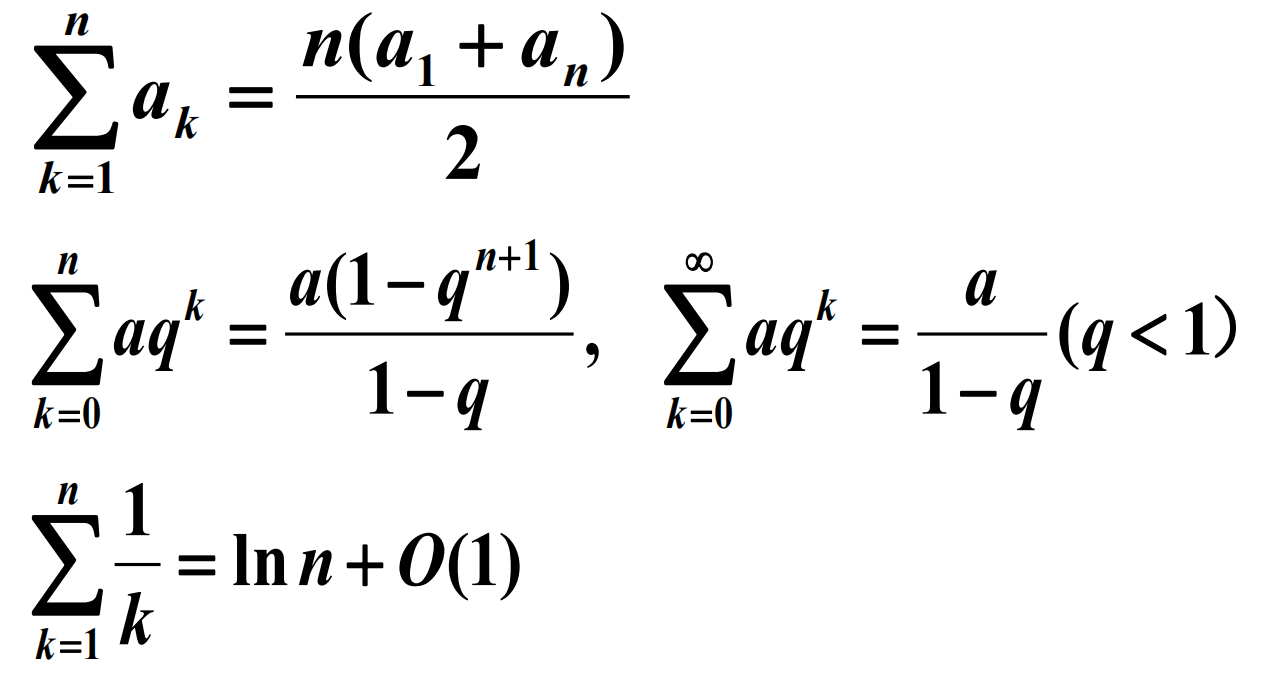
求和的例子

二分检索算法

二分检索运行实例
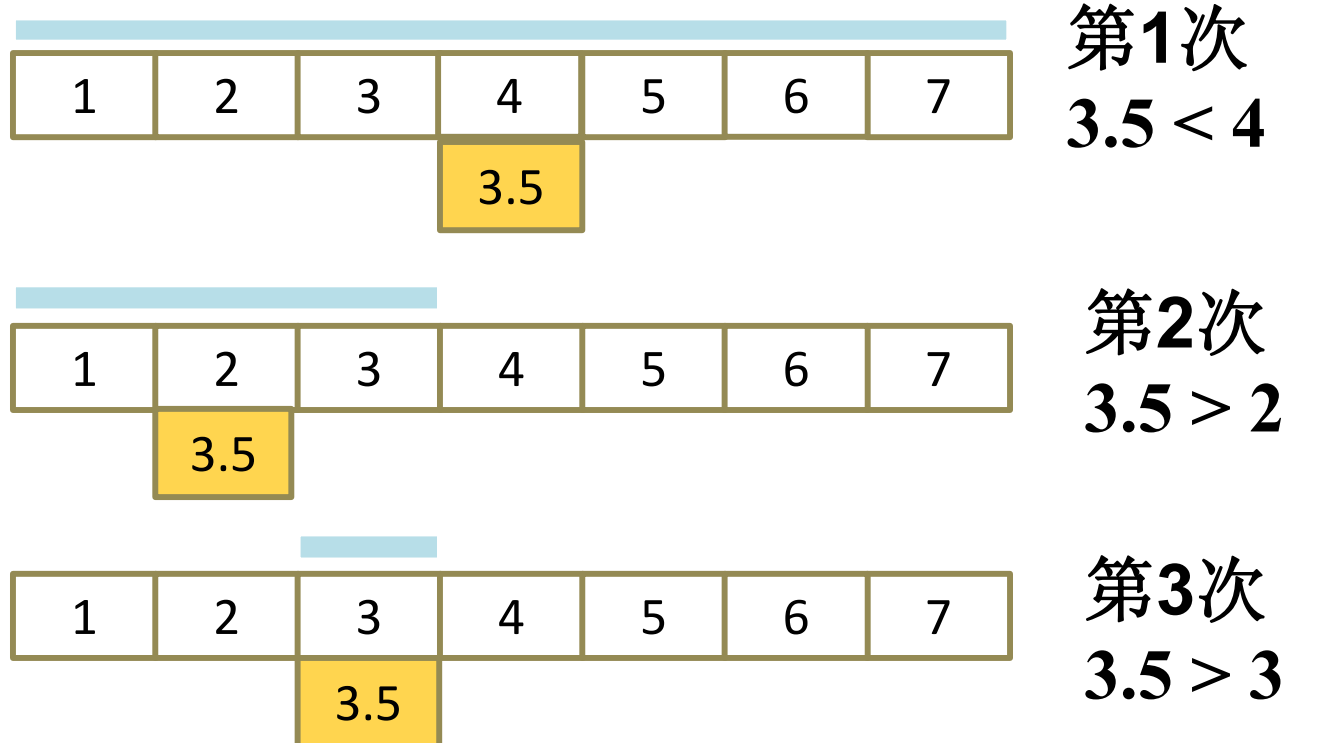
2 n +1个输入
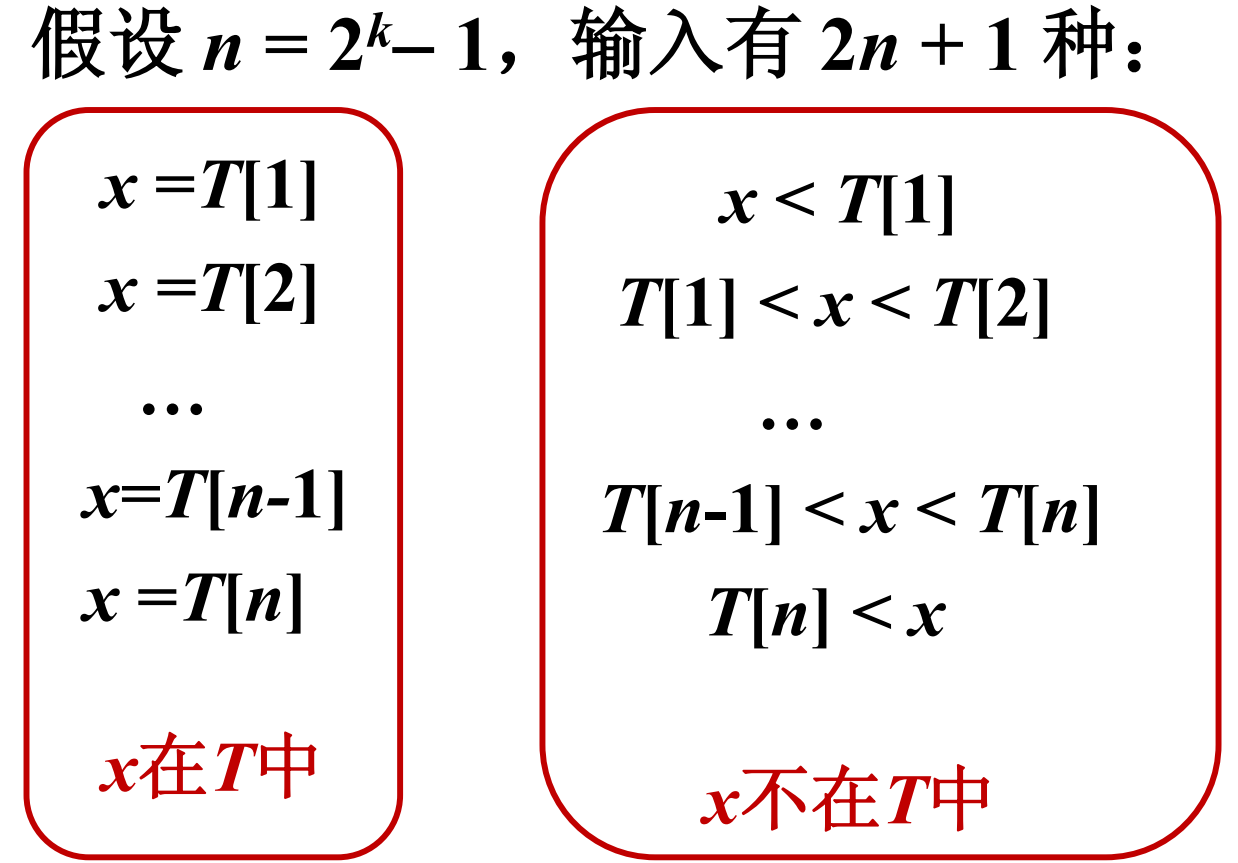
比较 t 次的输入个数
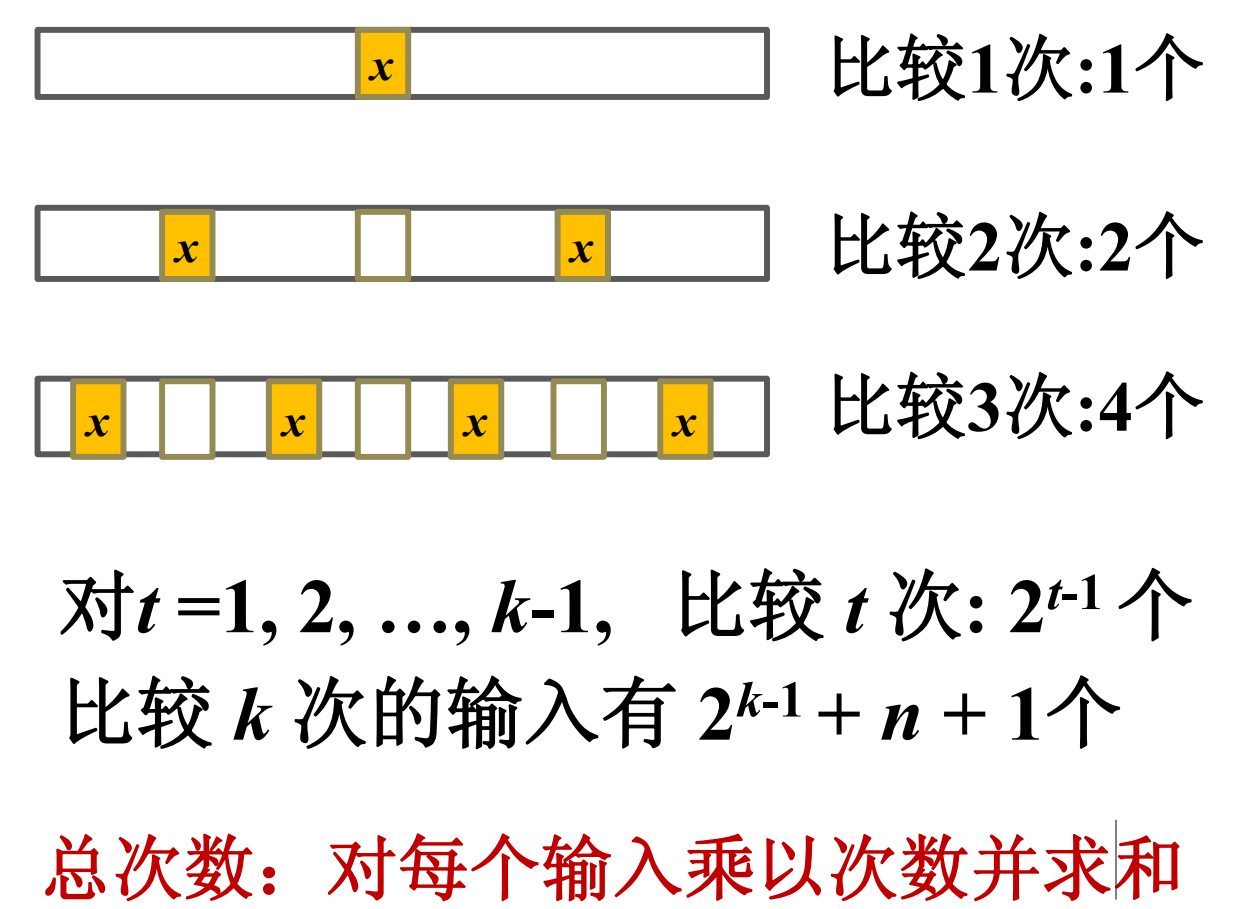
二分检索平均时间复杂度

估计和式上界的放大法
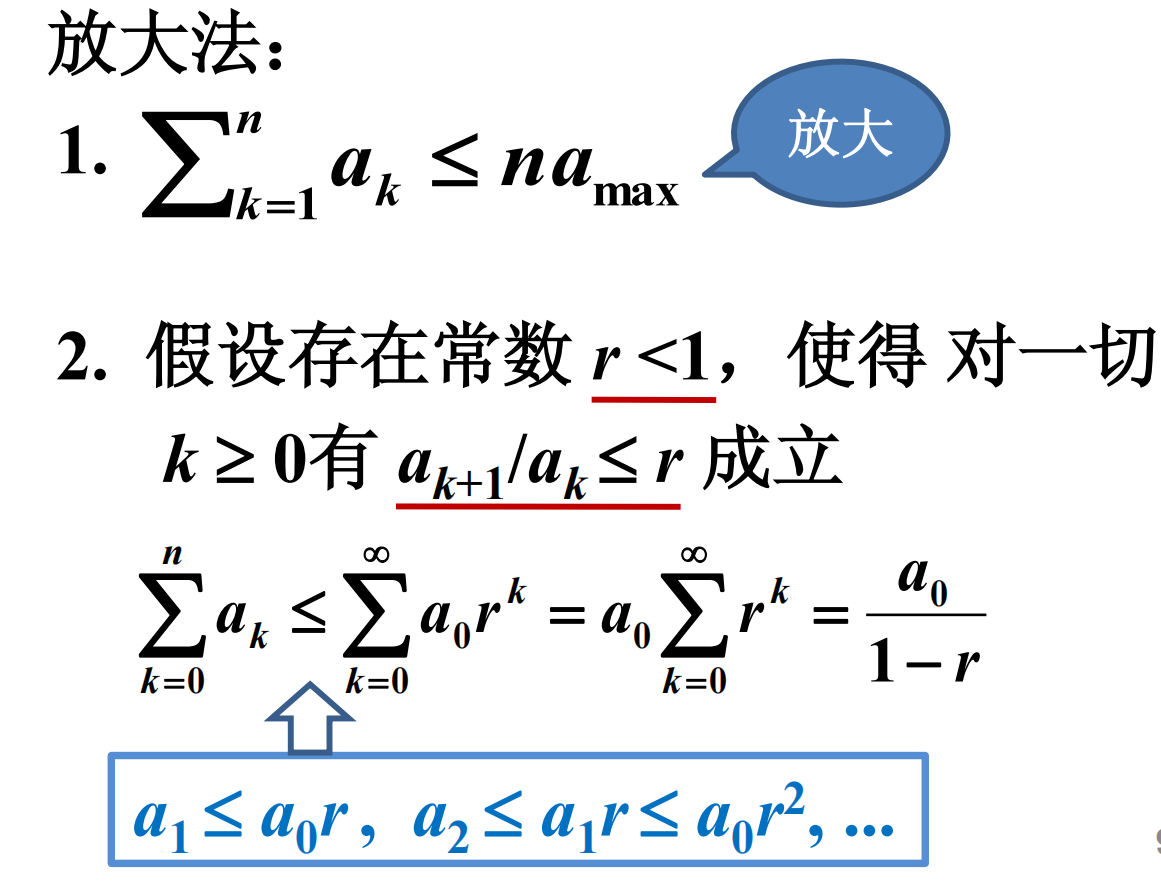
放大法的例子

估计和式渐近的界
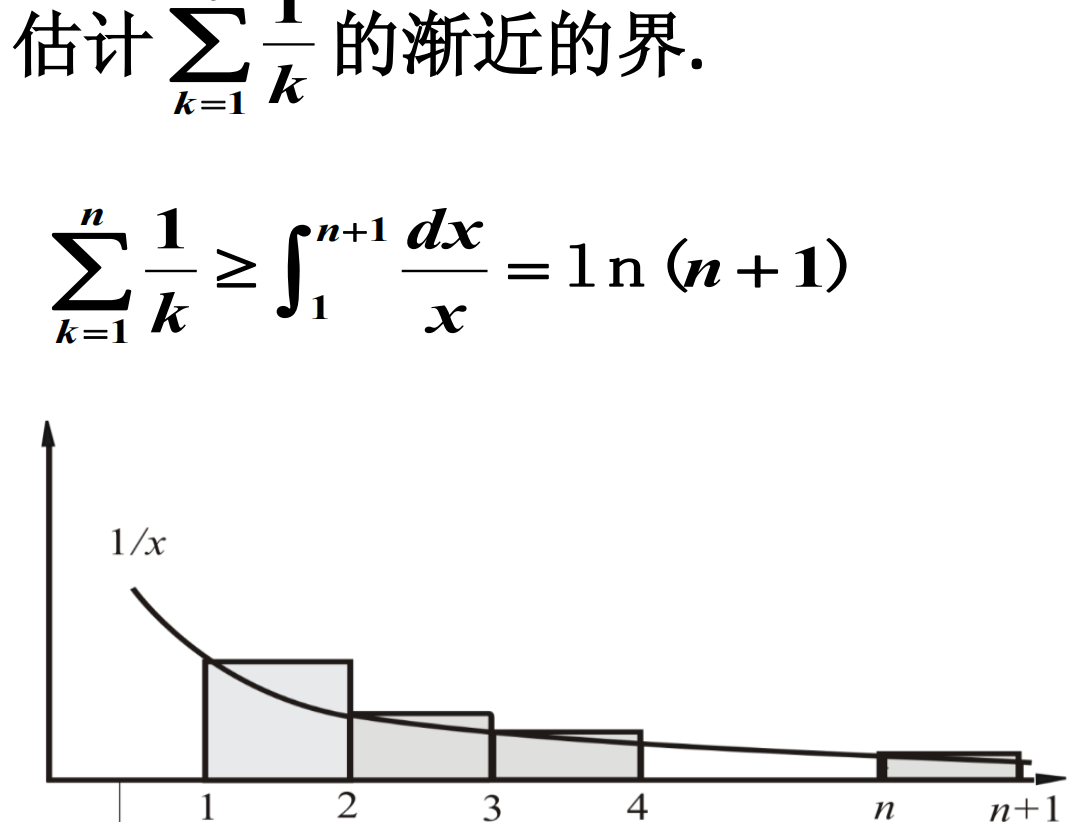
估计和式渐近的界
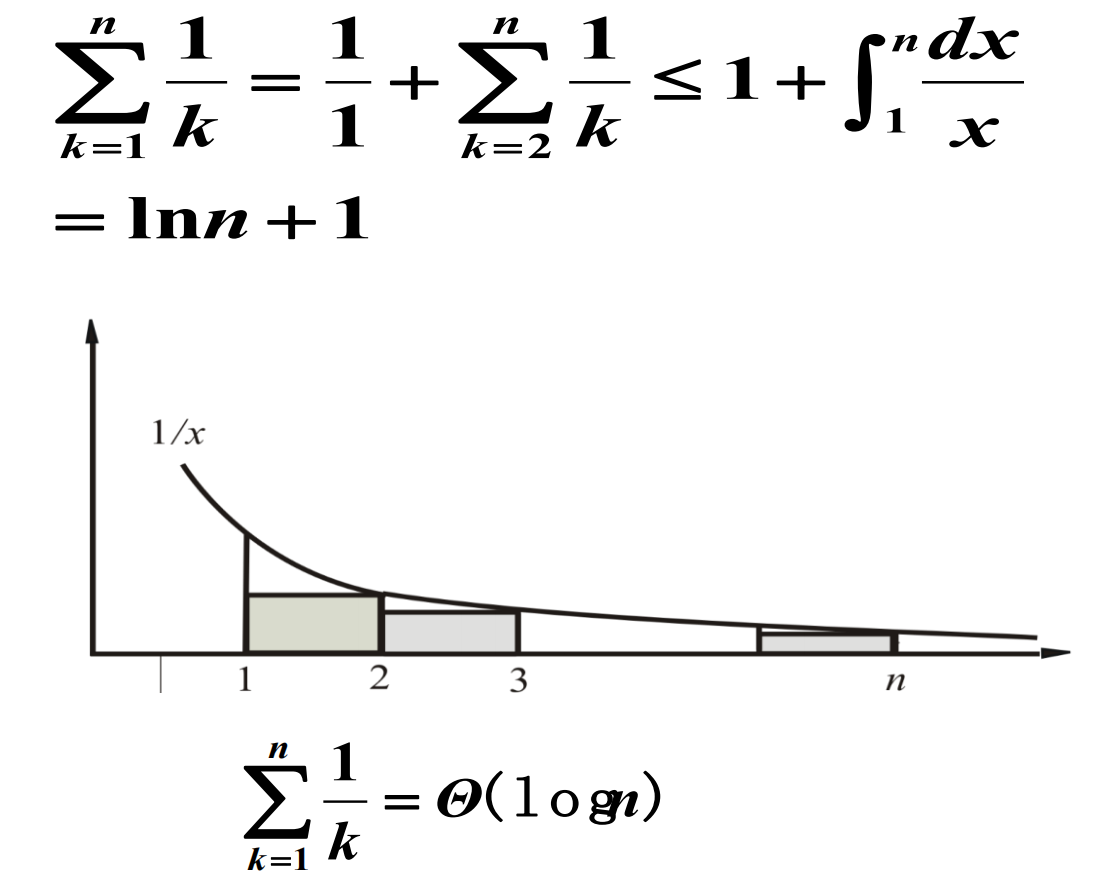
小结
• 序列求和基本公式:
等差数列
等比数列
调和级数
• 估计序列和:
放大法求上界
用积分做和式的渐近的界
• 应用:计数循环过程的基本运算次数
递推方程与算法分析
递推方程

递推方程的例子

Fibonacci数的存在
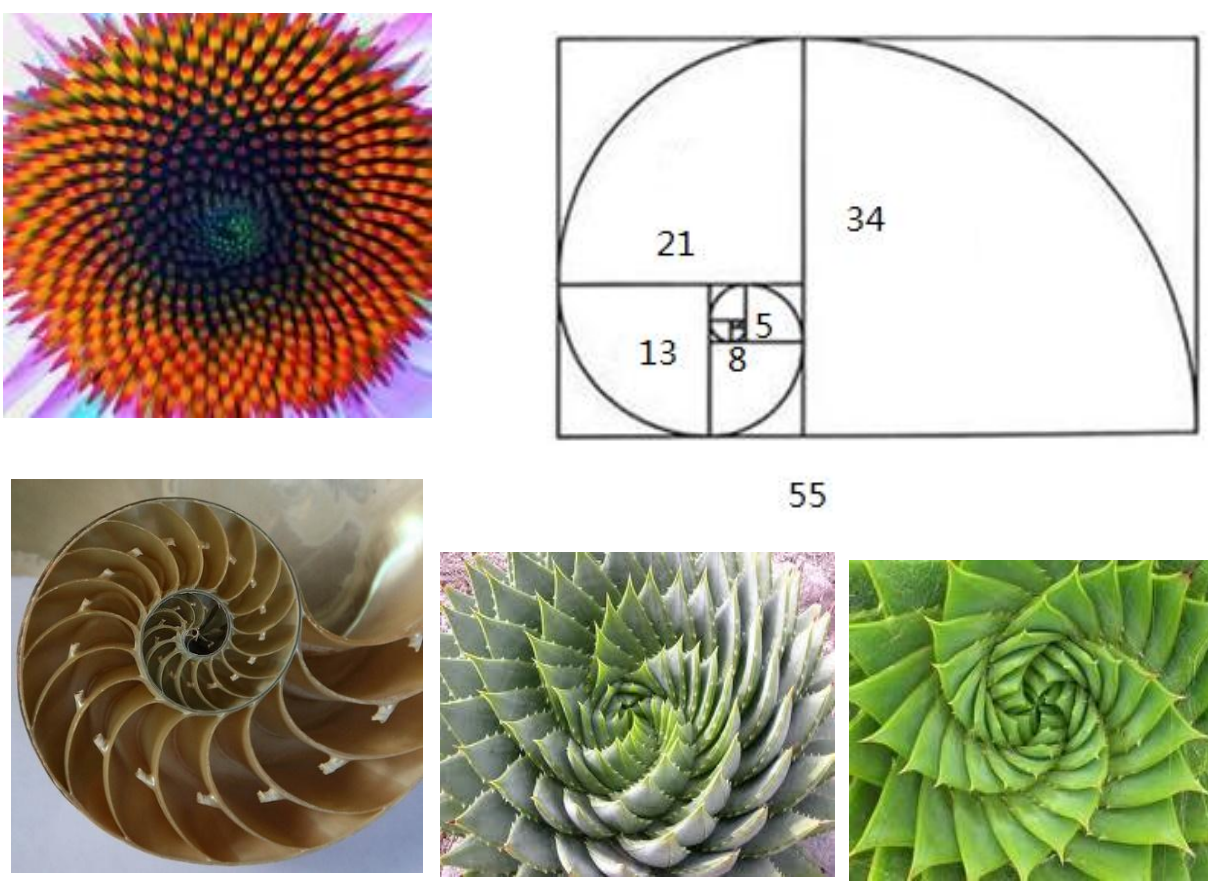
Hanoi塔问题
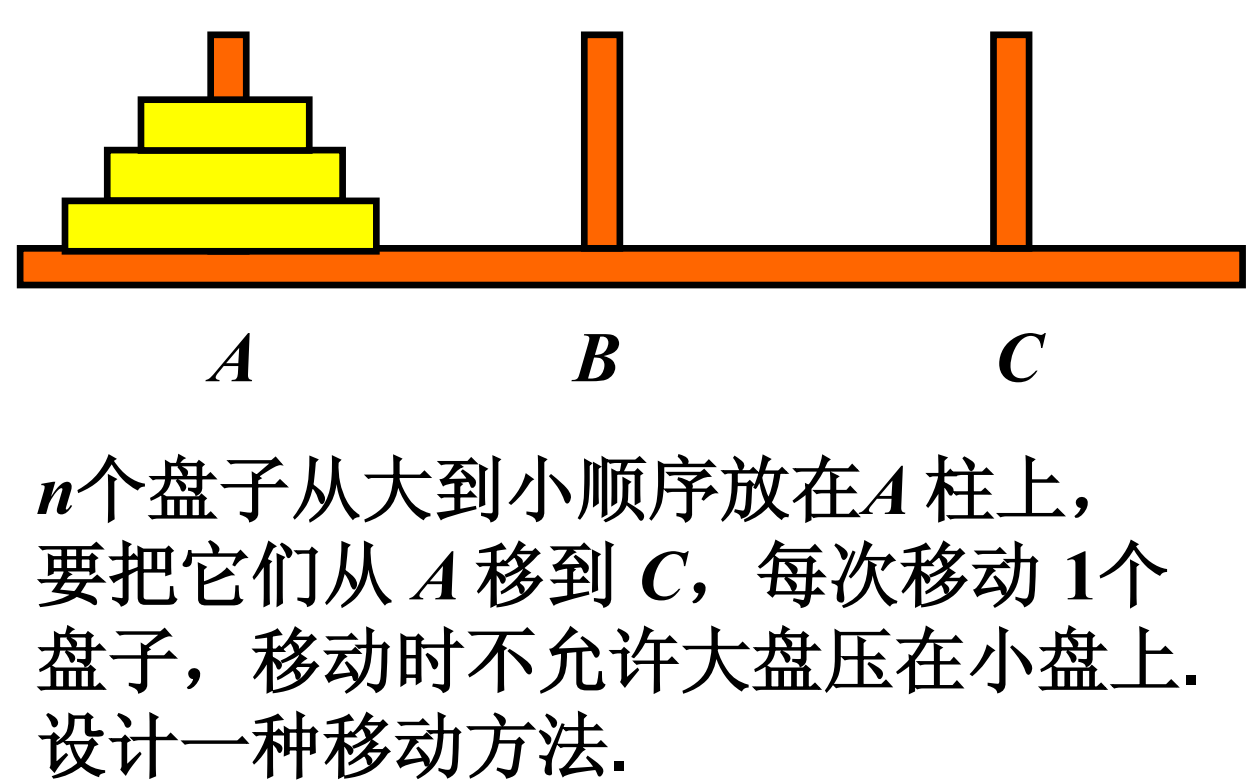
递归算法

分析算法

插入排序

最坏情况下时间复杂度
插入排序:
设基本运算是元素比较,对规模为 n
的输入最坏情况下的时间复杂度 W ( n )
W ( n )= W ( n -1)+ n -1 W (1)=0
解为 W ( n ) = n ( n -1)/2
小结
•递推方程的定义及初值
•递推方程与算法时间复杂度的关系
Hanoi塔的递归算法 插入排序的迭代算法
迭代法求解递推方程
迭代法
•不断用递推方程的右部替换左部
•每次替换,随着 n 的降低在和式中
多出一项
•直到出现初值停止迭代
•将初值代入并对和式求和
•可用数学归纳法验证解的正确性
Hanoi 塔算法

插入排序算法

换元迭代
•将对 n 的递推式换成对其他变元 k 的递推式
•对 k 直接迭代
•将解 (关于 k 的函数) 转换成关于 n 的函数
二分归并排序
MergeSort ( A , p , r )
输入:数组 A [ p … r ]
输出:按递增顺序排序的数组 A
1. if p < r
2. then q ( p+r )/2
3. MergeSort ( A , p , q )
4. MergeSort ( A , q +1, r )
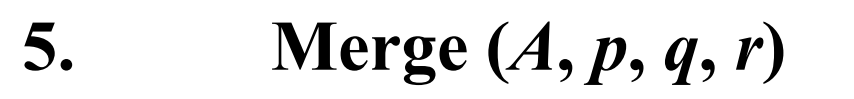
换元
假设 n =2 k , 递推方程如下:
W ( n )=2 W ( n /2)+ n 1
W (1)=0
换元:
W (2 k ) = 2 W (2 k -1 ) + 2 k 1
W (0) = 0
迭代求解

解的正确性-归纳验证
证明 : 下述递推方程的解是 W ( n )= n ( n 1)/2
W ( n )= W ( n 1)+ n 1
W (1)=0
方法:数学归纳法
证 n =1 , W (1)=1 (1 1)/2 = 0
假设对于 *n , *解满足方程,则
W ( n +1)
= W ( n )+ n = n ( n 1)/2 + n
= n [( n 1)/2+1] = n ( n +1)/2
小结
迭代法求解递推方程
• 直接迭代,代入初值,然后求和
• 对递推方程和初值进行换元,然
后求和,求和后进行相反换元,
得到原始递推方程的解
• 验证方法——数学归纳法
差消法化简高阶递推方程
快速排序
• 假设 A [ p … r ] 的元素彼此不等
以首元素 A [1] 对数组 A [ p…r ] 划分 , 使得:
小于 x 的元素放在 A [ p … q 1]
大于 x 的元素放在 A [ q +1… r ]
• 递归对 A [ p … q 1] 和 A [ q +1… r ] 排序
工作量: 子问题工作量+划分工作量
输入情况
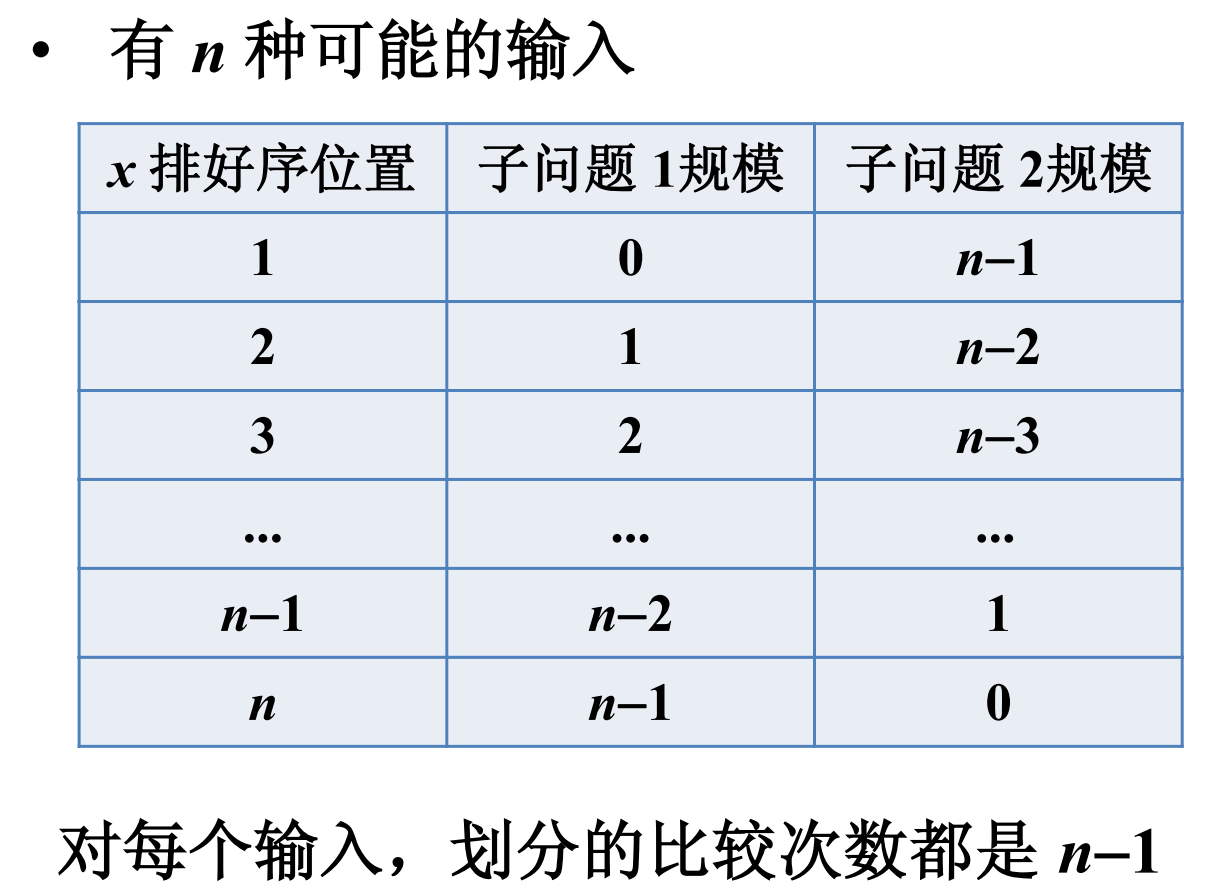
工作量总和
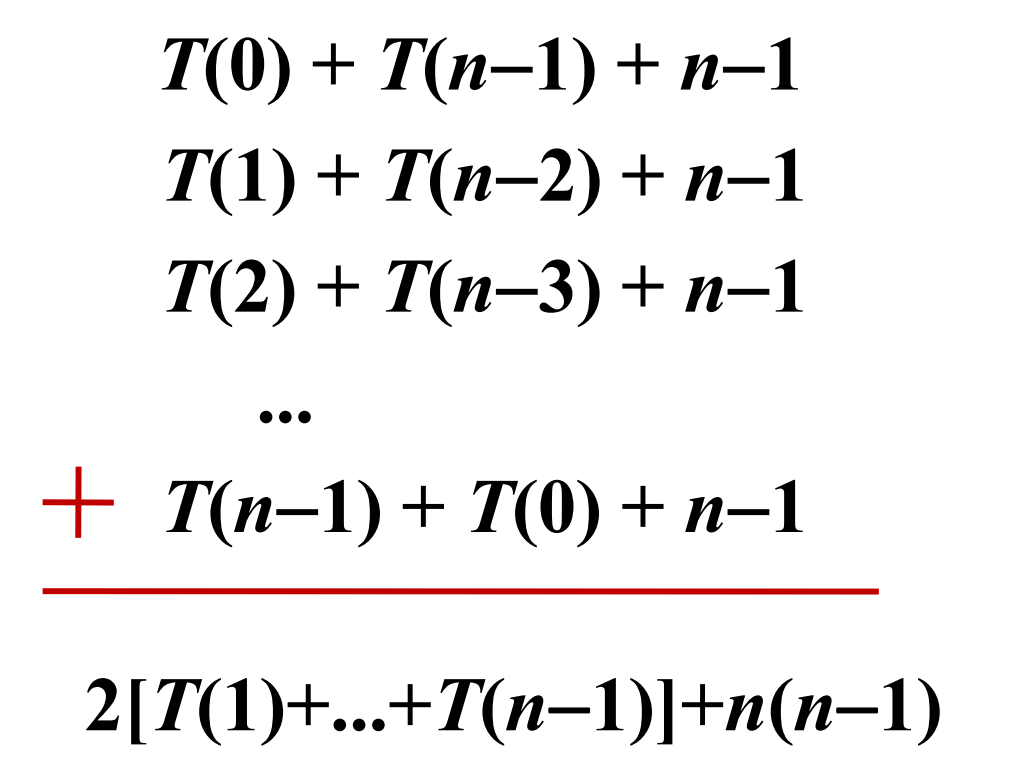
快速排序平均工作量
假设首元素排好序在每个位置是等
概率的
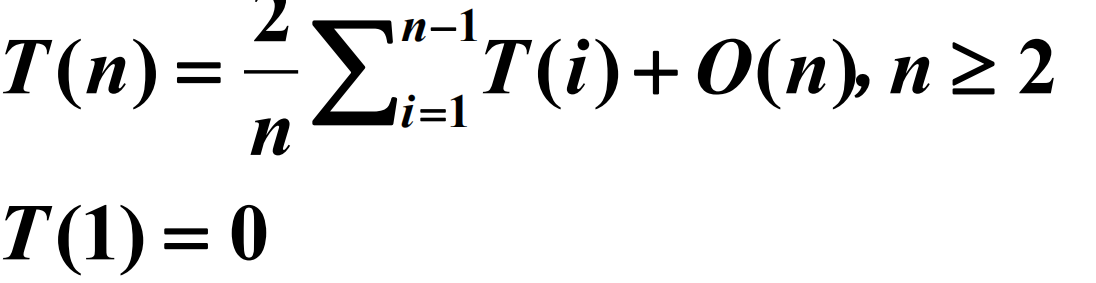
全部历史递推方程
对于高阶方程应该先化简,然后迭代
差消化简
利用两个方程相减,将右边的项尽可能
消去,以达到降阶的目的
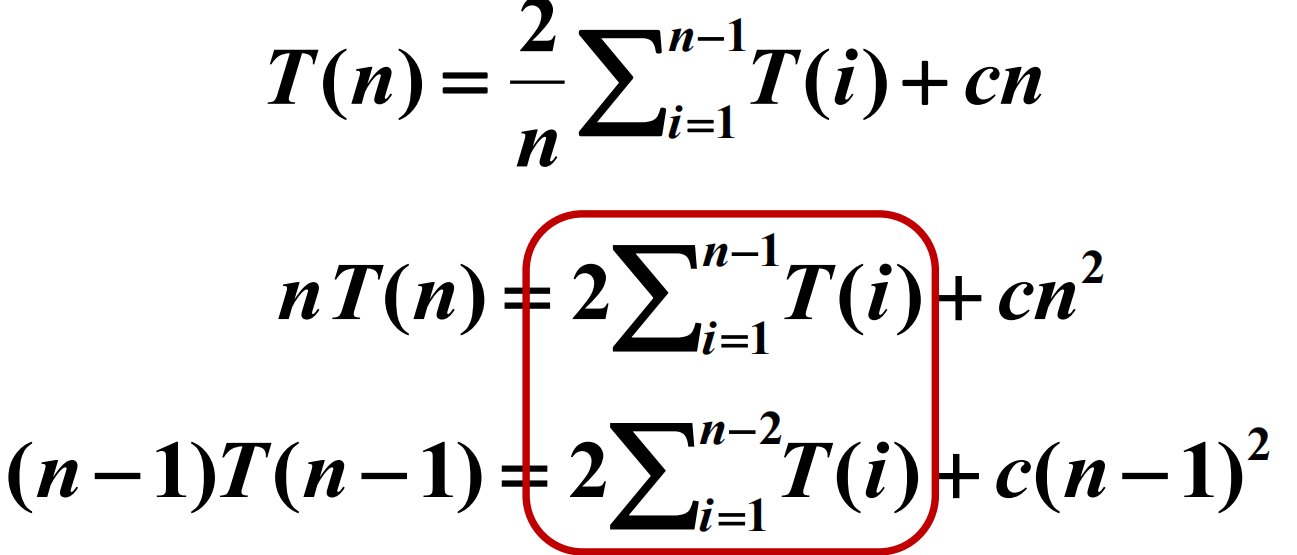
差消化简

迭代求解

小结
• 对于高阶递推方程先要用差消法化简为一阶方程
• 迭代求解
递归树
有关基 递归树的概念 本概
• 递归树是迭代计算的模型 .
• 递归树的生成过程与迭代过程一致 .
• 递归树上所有项恰好是迭代之后产
生和式中的项 .
• 对递归树上的项求和就是迭代后方
程的解.
迭代在递归树中的表示
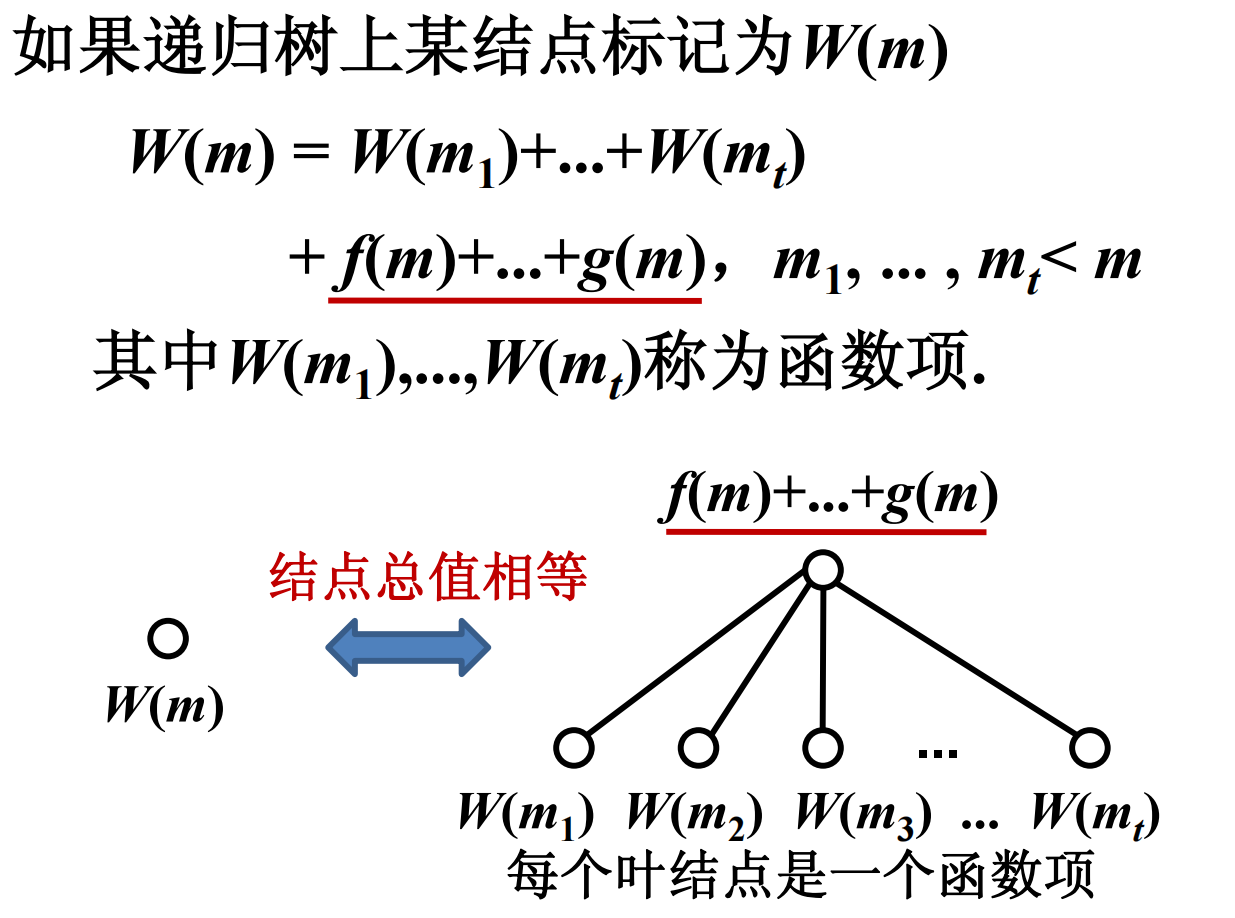
二层子树的例子
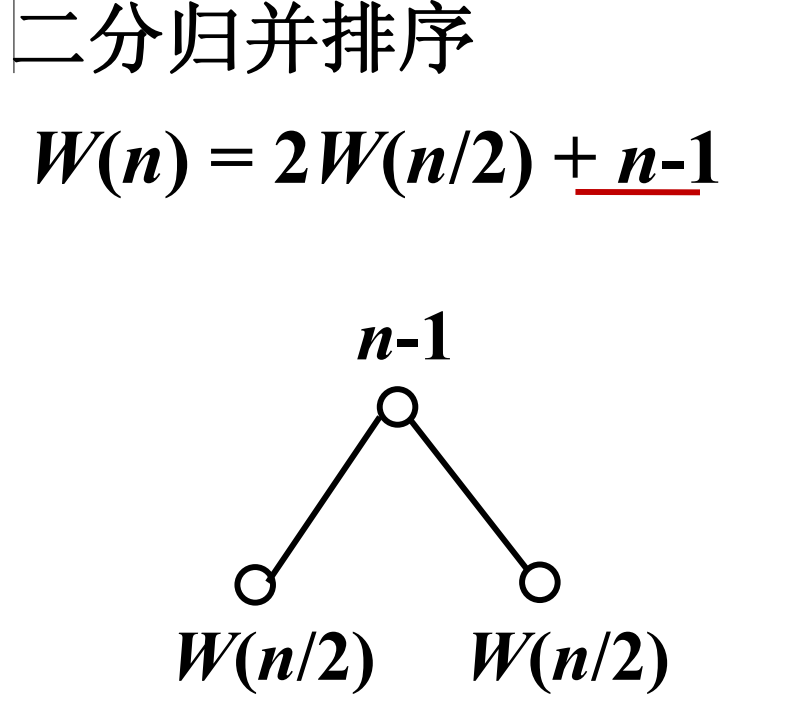
递归树的生成规则
• 初始,递归树只有根结点 , 其值为 W ( n )
• 不断继续下述过程:
将函数项叶结点的迭代式 W ( m ) 表示成二
层子树
用该子树替换该叶结点
• 继续递归树的生成,直到树中无函数项
(只有初值)为止.
递归树生成实例
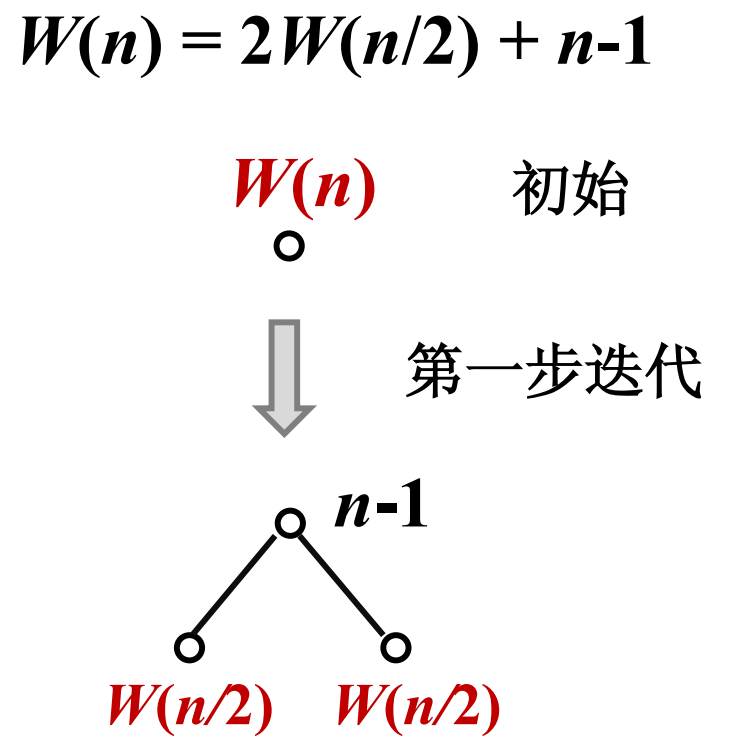
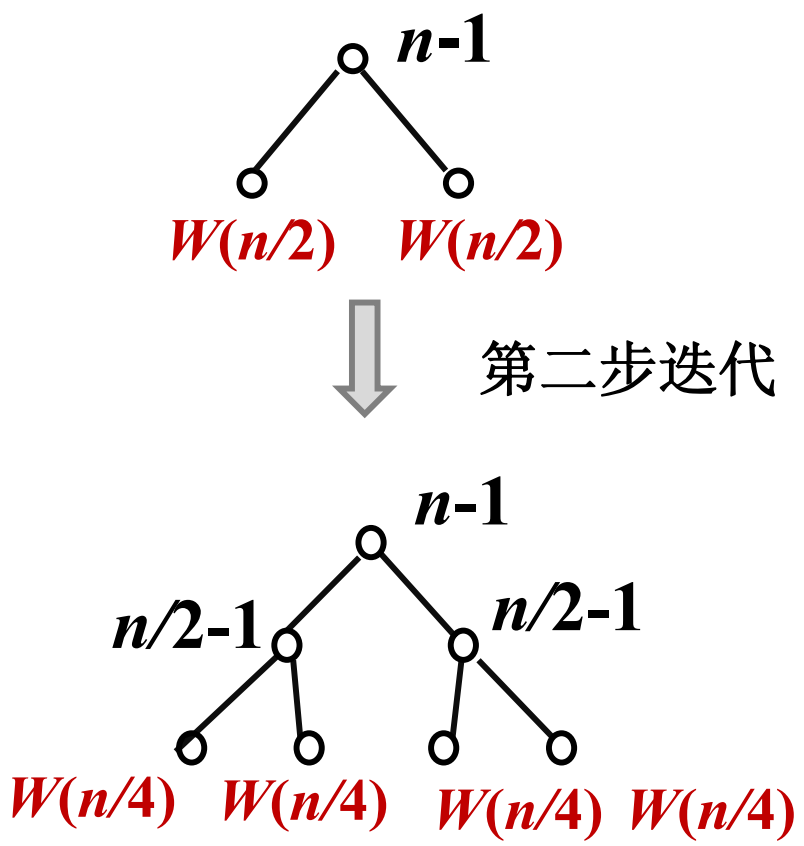
递归树
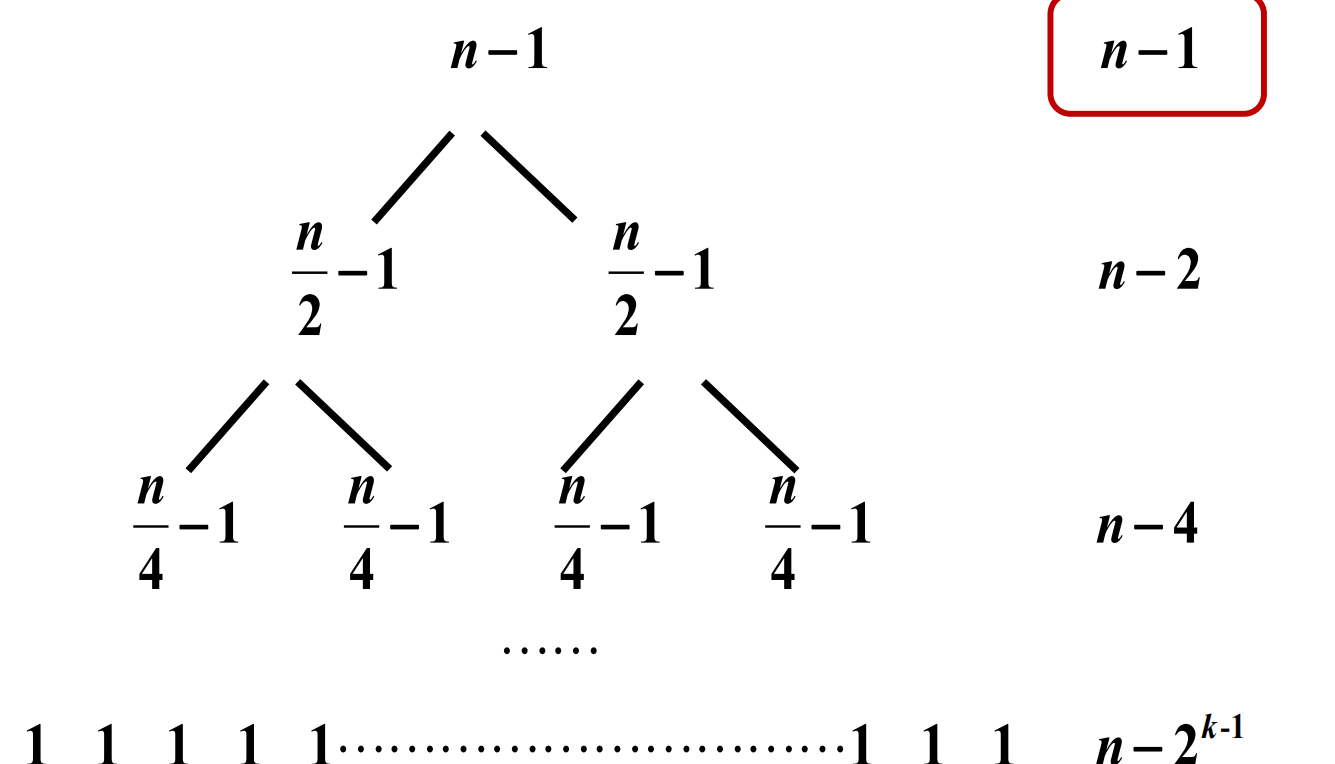
对递归树上的量求和
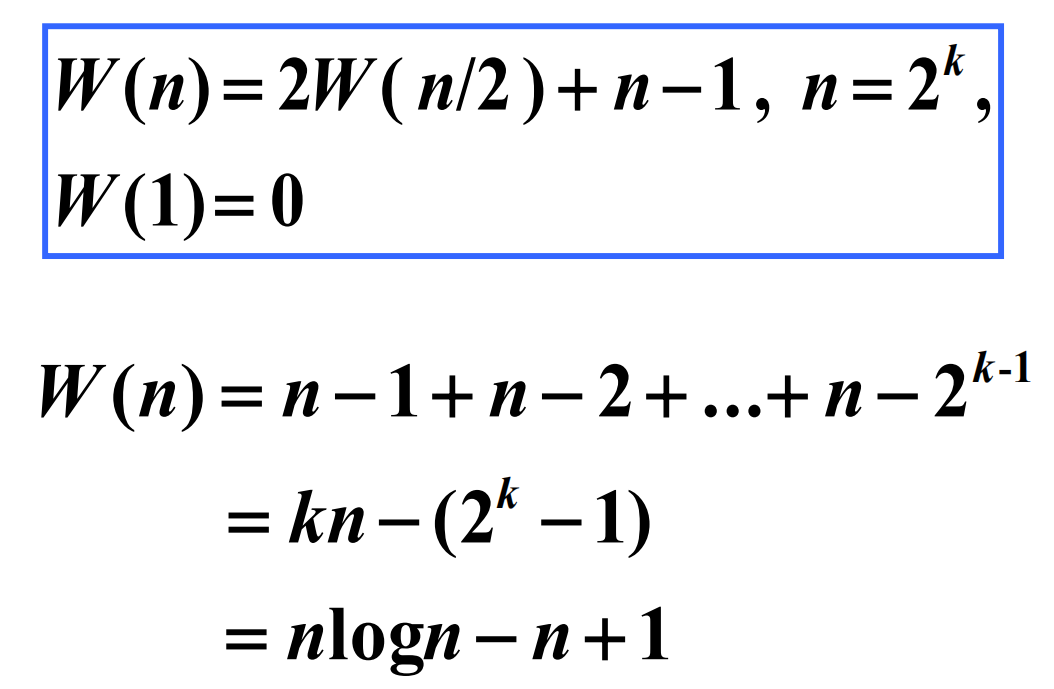
递归树应用实例
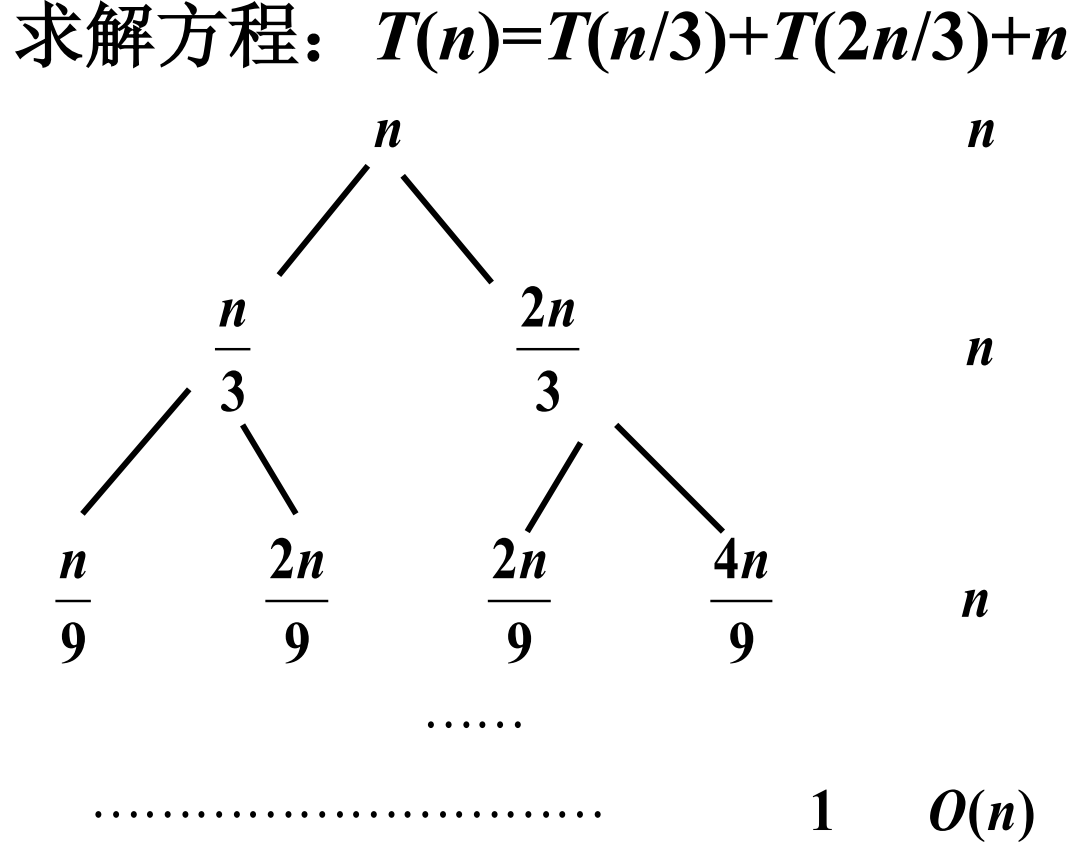
求和
方程: T ( n )= T ( n /3)+ T (2 n /3)+ n
递归树层数 k ,每层 O ( n )
******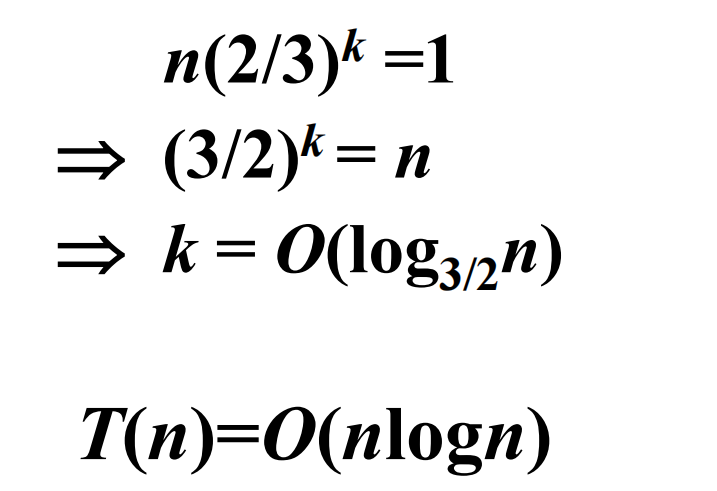
小结
• 递归树是迭代的图形表述
• 递归树的生成规则
• 如何利用递归树求解递推方程?
主定理及其证明
主定理的应用背景
求解递推方程
T ( n ) = a T ( n / b ) + f ( n )
a : 归约后的子问题个数
n/b :归约后子问题的规模
f ( n ) :归约过程及组合子问题的解的
工作量
二分检索: T ( n ) = T ( n /2)+1
二分归并排序: T ( n ) =2 T ( n /2)+ n -1
主定理

迭代

迭代结果



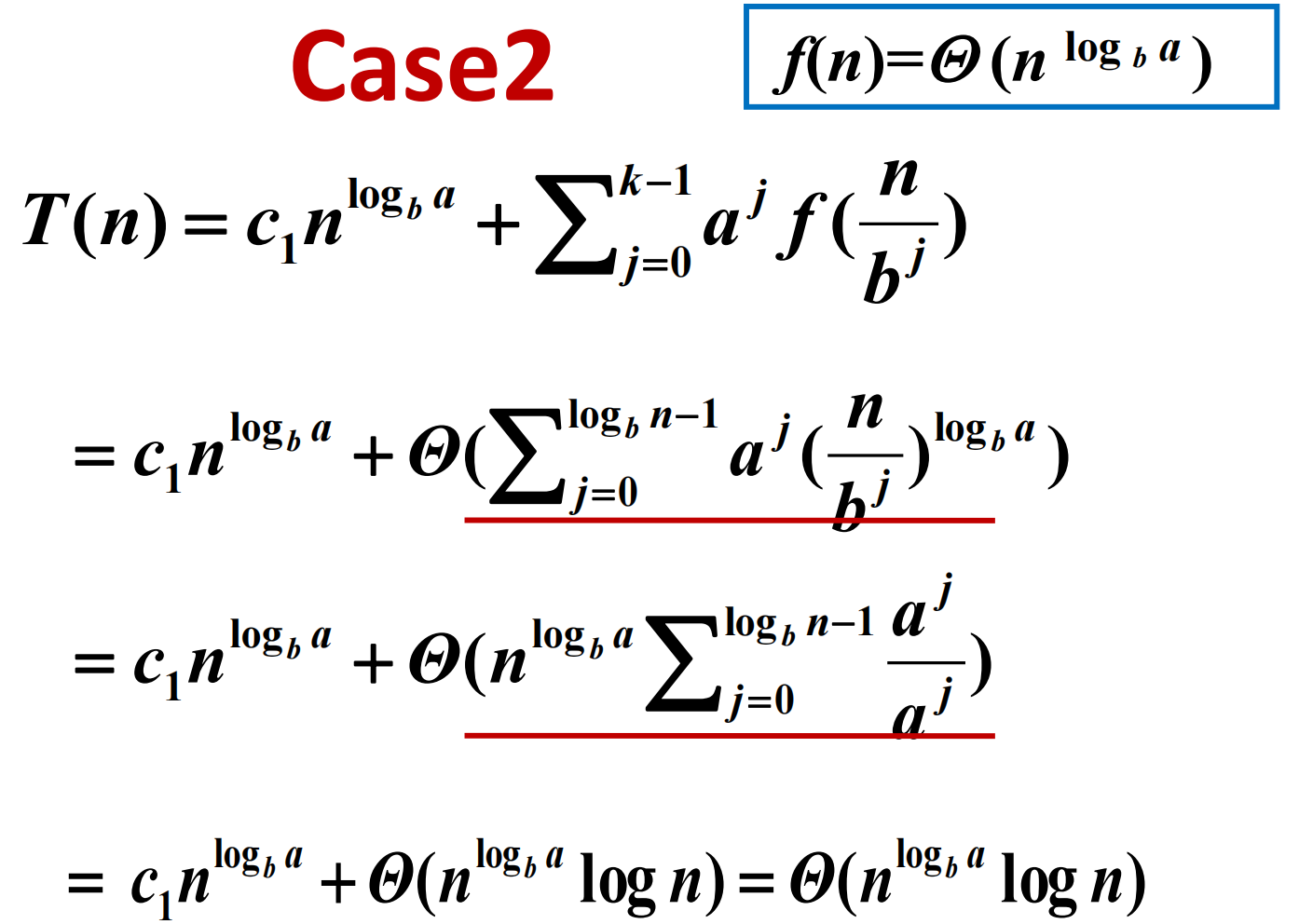


小结
• 主定理的应用背景
• 主定理的内容
• 主定理的证明
主定理的应用
求解递推方程:例1
例 1 求解递推方程
T ( n ) = 9 T ( n /3) + n
解 上述递推方程中的
a = 9 , b = 3 , f ( n ) = n
n log 3 9 = n 2 , f ( n ) = O ( n log 3 9-1 )
相当于主定理的 case1 ,其中 =1.
根据定理得到 T ( n ) = ( n 2 )
求解递推放出:例2
例 2 求解递推方程
T ( n ) = T (2 n /3) + 1
****求解递推方程:例2
解 上述递推方程中的
a = 1, b = 3/2, f ( n ) = 1 ,
n log 3/2 1 = n 0 = 1
相当于主定理的
Case2 .
根据定理得到 T ( n ) = ( log n )

条件验证

递归算法分析

不能使用主定理的例子

递归树求解
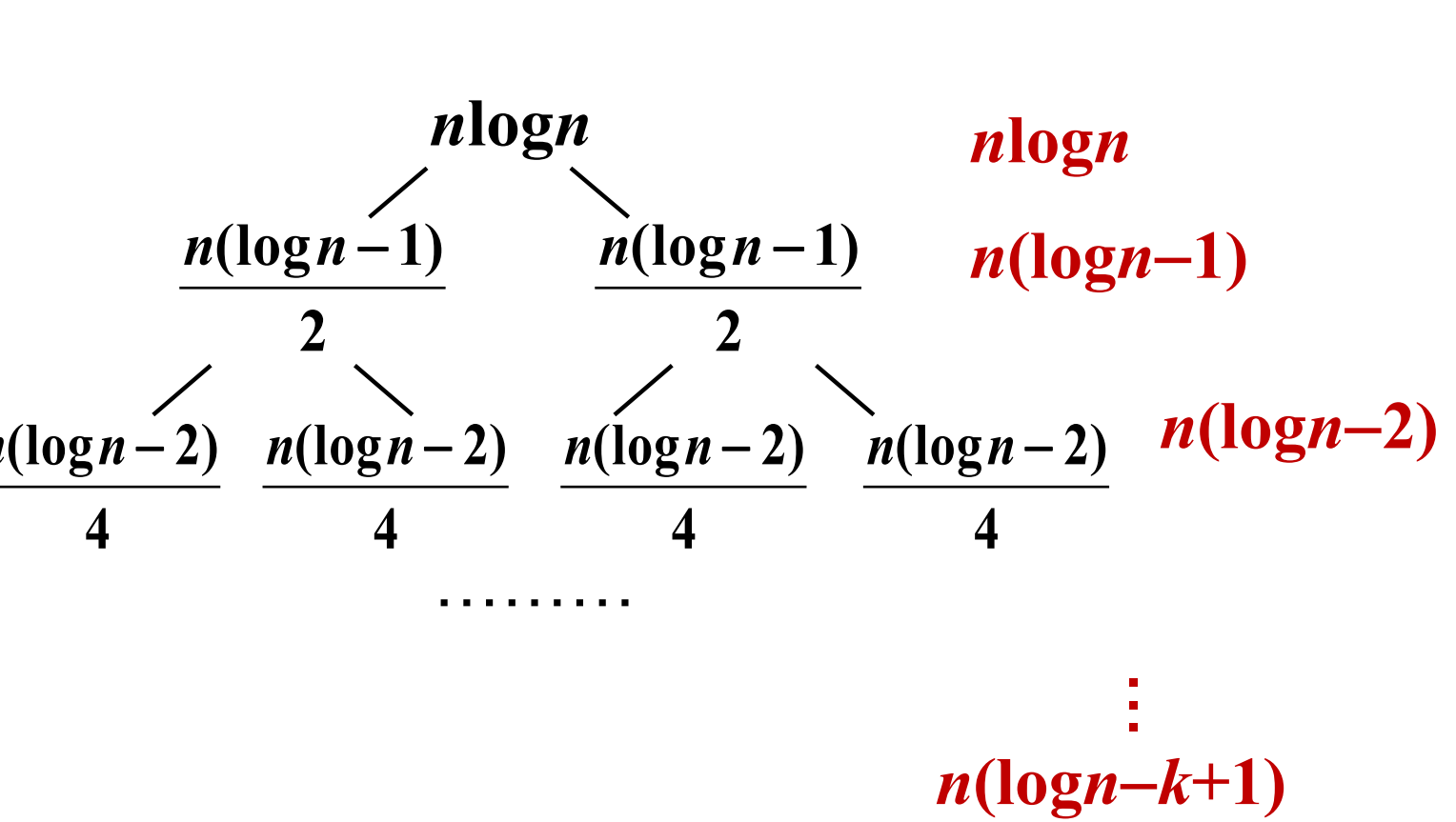
求和
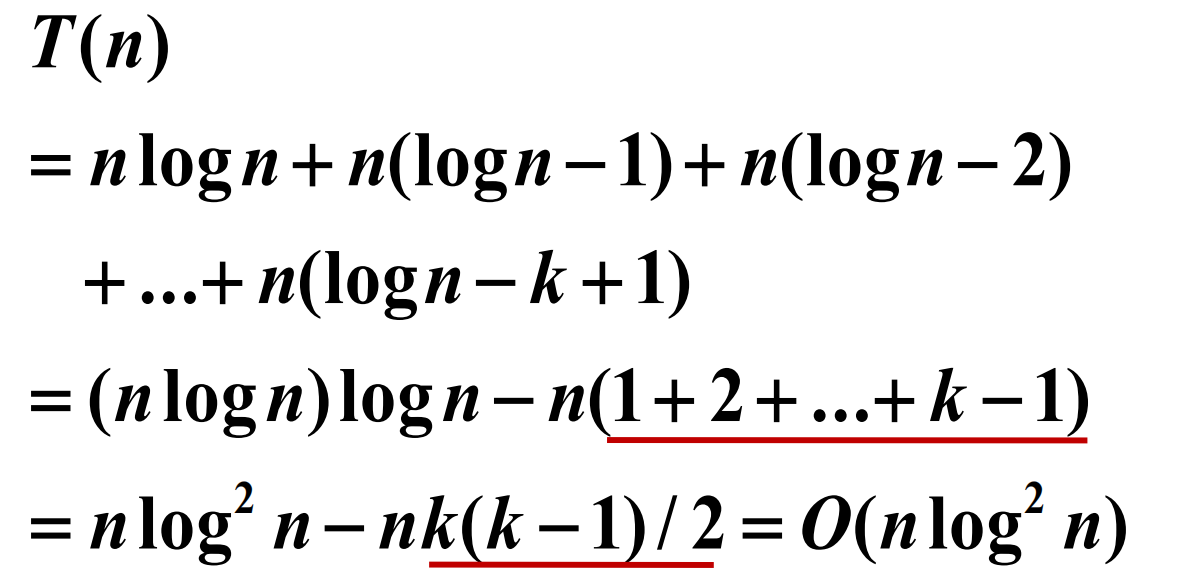
小结
• 使用主定理求解递推方程需要
满足什么条件?
• 主定理怎样用于算法复杂度分
析?
相关文章:
算法设计与分析(屈婉玲)视频笔记day2
序列求和的方法 数列求和公式 等差、等比数列与调和级数 求和的例子 二分检索算法 二分检索运行实例 2 n 1个输入 比较 t 次的输入个数 二分检索平均时间复杂度 估计和式上界的放大法 放大法的例子 估计和式渐近的界 估计和式渐近的界 小结 • 序列求和基本公式:…...

14-PHP使用过的函数 131-140
131、session_unset 释放当前会话注册的所有会话变量。 没有返回值。 132、session_destroy 销毁当前会话中的全部数据, 但是不会重置当前会话所关联的全局变量, 也不会重置会话 cookie。 如果需要再次使用会话变量, 必须重新调用 session_…...

【第39天】实现一个冒泡排序
本文已收录于专栏 🌸《Java入门一百例》🌸 学习指引 序、专栏前言一、冒泡排序一、【例题1】1、题目描述2、解题思路3、模板代码三、推荐专栏序、专栏前言 本专栏开启,目的在于帮助大家更好的掌握学习Java,特别是一些Java学习者难以在网上找到系统地算法学习资料帮助自身…...

「2」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 方阵的行列式 (1) |A^T||A|(2) |ǖ…...

动态规划专题——背包问题
🧑💻 文章作者:Iareges 🔗 博客主页:https://blog.csdn.net/raelum ⚠️ 转载请注明出处 目录前言一、01背包1.1 使用滚动数组优化二、完全背包2.1 使用滚动数组优化三、多重背包3.1 使用二进制优化四、分组背包总结…...

数据的分组聚合
1:分组 t.groupby #coding:utf-8 import pandas as pd import numpy as np file_path./starbucks_store_worldwide.csv dfpd.read_csv(file_path) #print(df.head(1)) #print(df.info()) groupeddf.groupby(byCountry) print(grouped) #DataFrameGroupBy #可以遍历…...
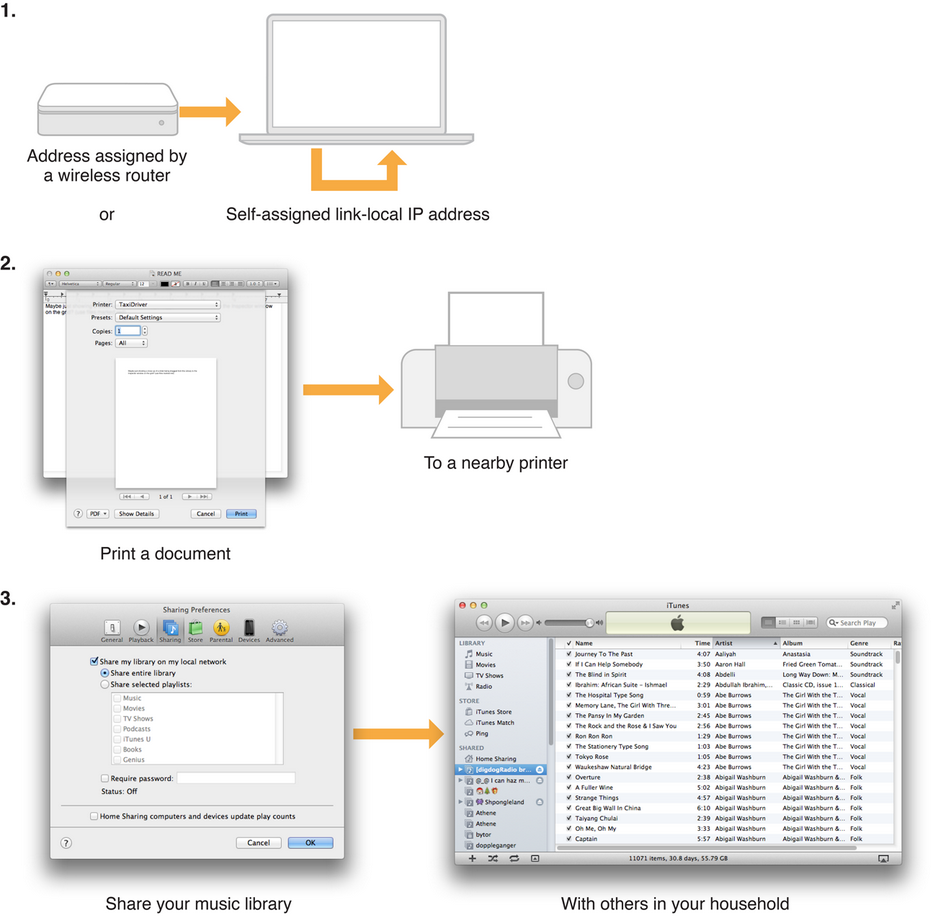
【Airplay_BCT】Bonjour conformance tests苹果IOT
从Airplay开始,接触到BCT,这是什么?被迫从安卓变成ios用户和开发。。。开始我的学习之旅,记录成长过程,不定时更新 Bonjour 下面是苹果官网关于bonjour的解释 Bonjour, also known as zero-configuration networking, …...
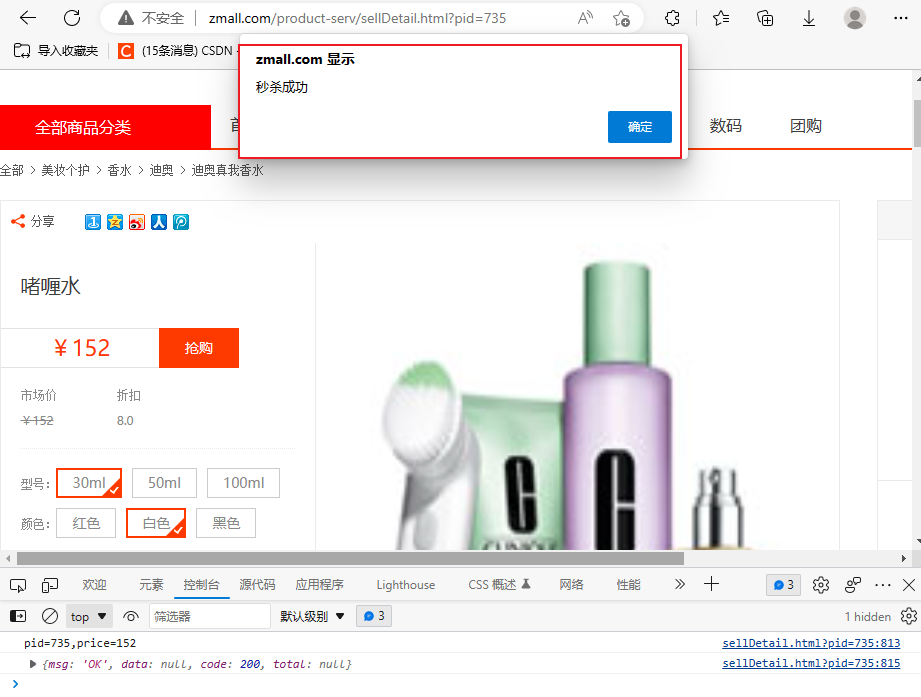
开发微服务电商项目演示(五)
登录方式调整第1步:从zmall-common的pom.xml中移除spring-session-data-redis依赖注意:本章节中不采用spring-session方式,改用redis直接存储用户登录信息,主要是为了方便之后的jmeter压测;2)这里只注释调用…...

Git删除大文件历史记录
Git删除大文件历史记录 git clone 仓库地址 查看大文件并排序 git rev-list --objects --all |grep $(git verify-pack -v .git/objects/pack/pack-*.idx | sort -k 3 -g | tail -1|awk {print $1})删除大文件 git filter-branch --force --index-filter git rm --cached --ig…...
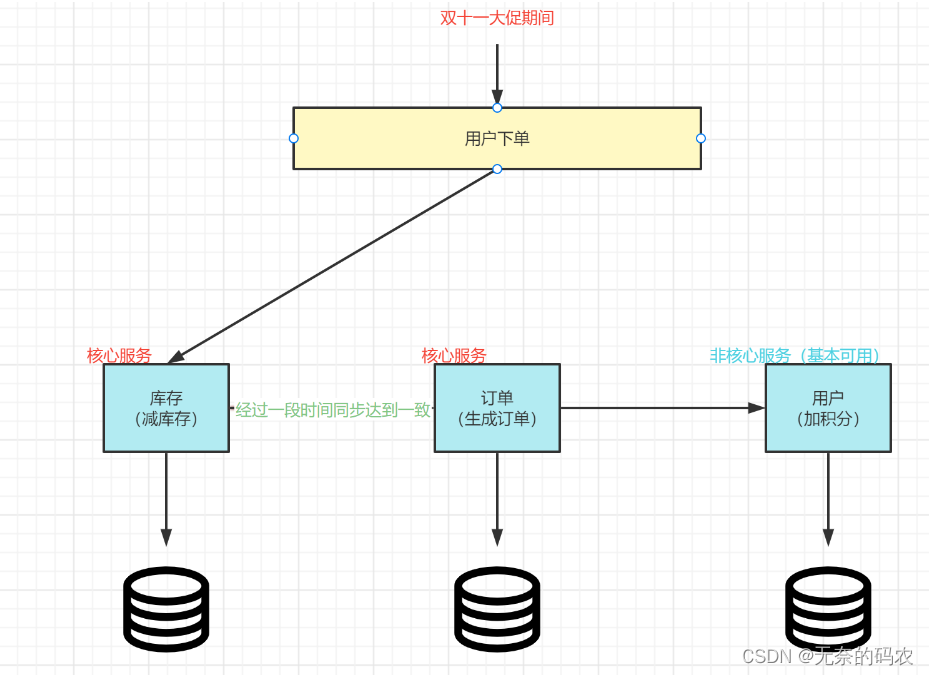
Seata-Server分布式事务原理加源码(一) - 微服务之分布式事务原理
概念 基础概念:事务ACID • A(Atomic):原子性,构成事务的所有操作,要么都执行完成,要么全部不执行,不可能出现部分成功部分失 败的情况。 • C(Consistency)…...

【ZooKeeper】zookeeper源码9-ZooKeeper读写流程源码分析
源码项目zookeeper-3.6.3:核心工作流程ZooKeeper选举和状态同步结束之后的服务启动ZooKeeper SessionTracker启动和工作机制ZooKeeper选举和状态同步结束之后的服务启动 在Leader的lead()方法的最后,即Leader完成了和集群过半Follower的同步之后&#x…...

Python实现批量导入xlsx数据1000条
遇到的问题:用户批量导入数据1000条,导入不成功的问题,提示查询不到商品资料。这个场景需要依靠批量的数据,每次测试的时候需要手动生成批量的数据,然后再导入操作,费时费劲。所以写了个脚本来实现。在前面…...
Ubuntu20.04安装redis与远程连接
一、安装Redis5.7 1、安装Redis apt-get install redis-server2、安装完成后,Redis服务器会自动启动。查看redis是否启动成功 service redis-server status #查看状态如下显示Active:active(running)状态:表示redis已在运行,启动成功。 …...

SAS应用入门学习笔记5
input 操作符: 代码说明: 1)1 表示第1列字符;7表示第7列字符; 2)col1 表示第一列数据;col2 表示第二列数据; 3)4.2 表示的是4个字符,2表示小数点后两位&a…...
PHP新特性集合
php8新特性命名参数function foo(string $a, string $b, ?string $c null, ?string $d null) { /* … */ }你可以通过下面的方式传入参数进行调用foo(b: value b, a: value a, d: value d, );联合类型php7class Number {/** var int|float */private $number;/*** param f…...
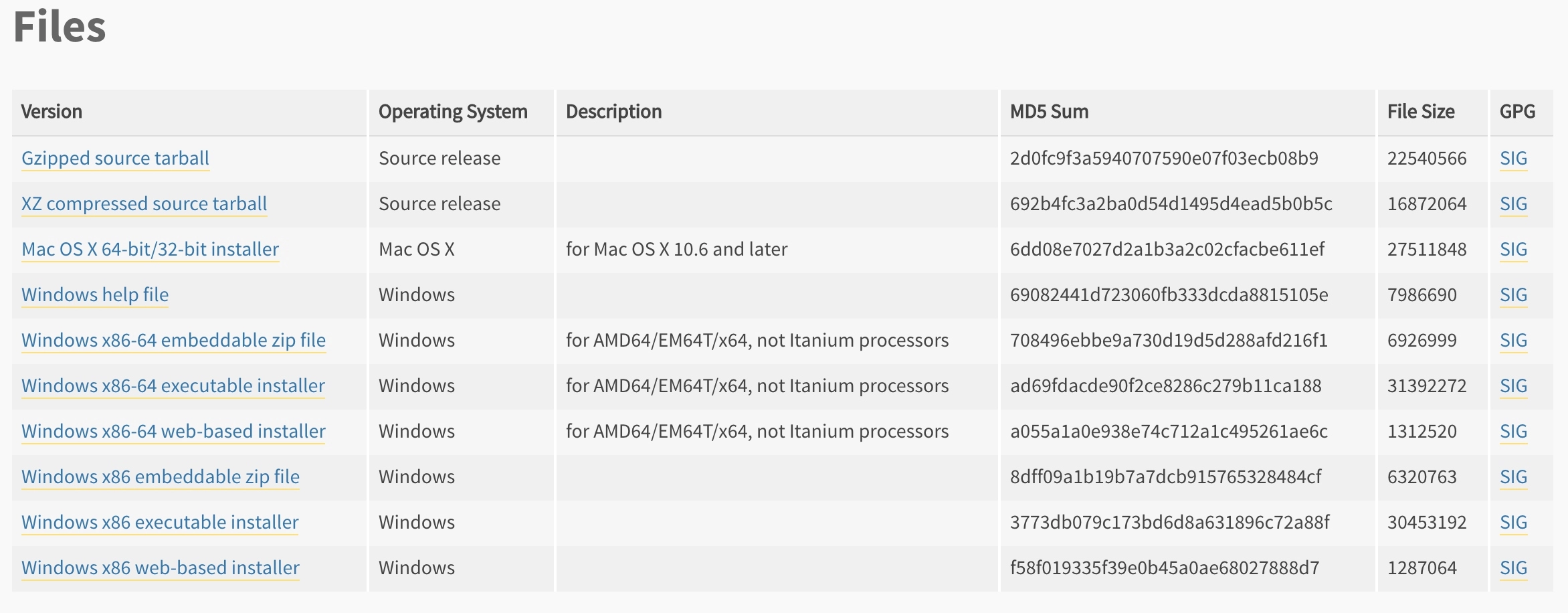
【开发环境配置】--Python3的安装
1-开发环境配置 工欲善其事,必先利其器! 编写和运行程序之前,我们必须先把开发环境配置好。只有配置好了环境并且有了更方便的开发工具,我们才能更加高效地用程序实现相应的功能。然而很多情况下,我们可能在最开始就…...

postman实现接口测试详细教程
各位小伙伴大家好, 今天为大家带来postman实战接口测试详细教程 一、通过接口文档集合抓包分析接口 通过fiddler抓包获取到注册接口URL地址及相关参数数据,并通过接口文档分析接口参数内容及参数说明, 如有必要的依赖条件必须进行梳理, 如token等 Fiddler抓包注册接口请求与…...
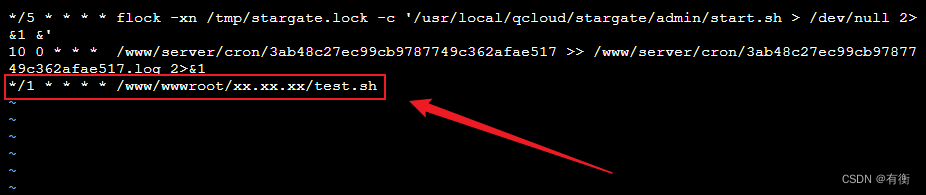
使用crontab执行定时任务
本来这个东西是挺简单的,是我脑子一直没转过来弯,我就想看看有多少人跟我一样😏 crontab语法自己去菜鸟教程看看就知道了,没什么难度 需求:每分钟定时执行一个PHP文件或者一个PHP命令 这是需要执行的文件࿰…...
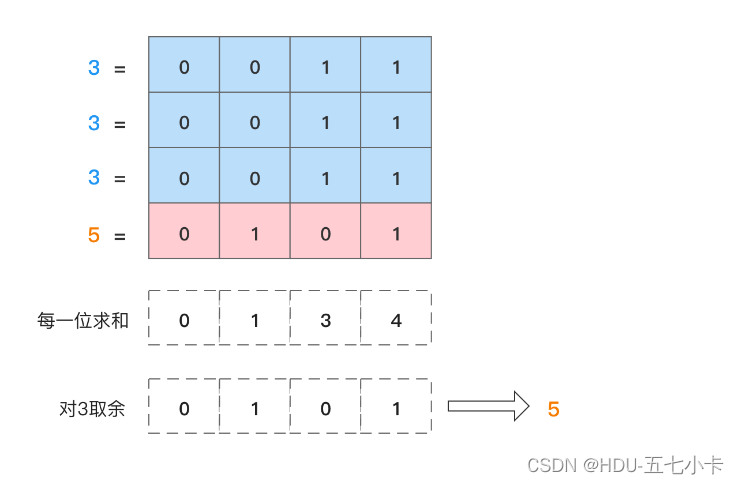
剑指 Offer 56 - II. 数组中数字出现的次数 II
题目 在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。 思路 这题是剑指 Offer 56 - I. 数组中数字出现的次数的变体,本题只有一个数num出现一次,其余的均出现三次 三次的话使用异或消无法…...

C语言学习笔记(八): 自定义数据类型
结构体变量 什么是结构体 C语言允许用户自己建立由不同类型数据组成的组合型的数据结构,它称为结构体 结构体的成员可以是任何类型的变量,如整数,字符串,浮点数,其他结构体,指针等 struct Student //s…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
