实验04:图像压缩(DP算法)
1.实验目的:
掌握动态规划算法的基本思想以及用它解决问题的一般技巧。运用所熟悉的编程工具,运用动态规划的思想来求解图像压缩问题。
2.实验内容:
给定一幅图像,求解最佳压缩,使得压缩后的文件最小。
3.实验要求:
实现lena512.raw(称为原文件)图像压缩并保存到文件(称为压缩文件)中。编写相应的解码器,对保存的文件解压出图像,并将解压图像存储为raw文件,通过图像浏览工具验证解压文件和原文件相同。分析压缩率(即 压缩文件大小 除以 原文件大小),分析算法的时间复杂度和空间复杂度。
□ \square □ 基础性实验 □ \square □ 综合性实验 ⊠ \boxtimes ⊠ 设计性实验
一、问题分析(模型、算法设计和正确性证明等)
设灰度图像共 n n n个像素值,灰度图像可以视作一个一维向量 P = { p 1 , p 2 , . . . . . . , p n } P=\{p_1, p_2, ...... , p_n\} P={p1,p2,......,pn},将n个像素分割成m个连续段 { S i } i = 1 m \{S_i\}_{i=1}^m {Si}i=1m.
其中,对第 i i i段 S i S_i Si有下列相关变量:
| 符号 | 表示含义 |
|---|---|
| l [ i ] l[i] l[i] | 段长,该段内包含像素个数 |
| b [ i ] b[i] b[i] | 该段中各像素位宽, b [ i ] = ⌈ log ( 1 + max p k ∈ S i p k ) ⌉ b[i]=\lceil {\log{(1+\max_{p_k \in S_i}{p_k}})} \rceil b[i]=⌈log(1+maxpk∈Sipk)⌉ |
约定每段长度 l [ i ] l[i] l[i]满足:$1\leq l[i] \leq 256 且 且 且b[i]\geq 1$.
已知: 0 ≤ p k ≤ 255 0\leq p_k \leq 255 0≤pk≤255,故 1 ≤ b [ i ] ≤ 8 1\leq b[i]\leq 8 1≤b[i]≤8
将 S i S_i Si编码压缩如下:
l [ i ] − 1 b [ i ] − 1 { p i + 1 , p i + 2 . . . . . . , p i + l [ i ] } 8 b i t s 3 b i t s l [ i ] × b [ i ] b i t s \begin{matrix} l[i]-1 & b[i]-1 & \{p_{i+1}, p_{i+2}......, p_{i+l[i]}\}\\ 8bits & 3bits & l[i]\times b[i]bits \end{matrix} l[i]−18bitsb[i]−13bits{pi+1,pi+2......,pi+l[i]}l[i]×b[i]bits
压缩完成后,共占用空间: l [ i ] × b [ i ] + 11 l[i]\times b[i] + 11 l[i]×b[i]+11
设 f ( { S i } 1 m ) f(\{S_i\}_1^m) f({Si}1m)表示压缩为 m m m个连续子段集合 { S i } 1 m \{S_i\}_1^m {Si}1m占用空间,则递归表达如下:
f ( { S i } 1 m ) = f ( { S i } 1 m − 1 ) + 11 (1) f(\{S_i\}_1^m)=f(\{S_i\}_1^{m-1})+11\tag1 f({Si}1m)=f({Si}1m−1)+11(1)
最优子结构性质
设最优分段为 { S i } i = 1 m \{S_i\}_{i=1}^m {Si}i=1m,其中第 m m m个分段 S m S_m Sm的长度为 l e n len len,则 { S i } i = 1 m − 1 \{S_i\}_{i=1}^{m-1} {Si}i=1m−1是子问题 { p 1 , p 2 , . . . . . . , p n − l e n } \{p_1, p_2, ......, p_{n-len}\} {p1,p2,......,pn−len}的最优分段,递归表达如下:
f ( { S i } i = 1 m ) = f ( { S i } i = 1 m − 1 ) + f ( { S m } ) (2) f(\{S_i\}_{i=1}^m)=f(\{S_i\}_{i=1}^{m-1})+f(\{S_m\})\tag2 f({Si}i=1m)=f({Si}i=1m−1)+f({Sm})(2)
简要证明过程如下:
假设 { S i } i = 1 m \{S_i\}_{i=1}^m {Si}i=1m为原问题最优分段,即 f ( { S i } i = 1 m ) f(\{S_i\}_{i=1}^m) f({Si}i=1m)值最小,但 { S i } i = 1 m − 1 \{S_i\}_{i=1}^{m-1} {Si}i=1m−1不是子问题的最优解。
则将其分段策略调整为最优解后, f ( { S i } i = 1 m − 1 ) f(\{S_i\}_{i=1}^{m-1}) f({Si}i=1m−1)值减少, f ( { S i } i = 1 m ) = f ( { S i } i = 1 m − 1 ) + f ( { S m } ) f(\{S_i\}_{i=1}^m)=f(\{S_i\}_{i=1}^{m-1})+f(\{S_m\}) f({Si}i=1m)=f({Si}i=1m−1)+f({Sm})值减少,与假设矛盾。
令g(n)表示像素序列{p_1, p_2, …, p_n}的最优分段占用空间,则有递归公式如下:
g ( n ) = min ( g ( n − k ) + k × b m a x + 11 ) , 1 ≤ k ≤ min ( n , 256 ) (3) g(n)=\min(g(n-k)+k\times b_{max}+11), 1\leq k \leq \min{(n, 256)}\tag3 g(n)=min(g(n−k)+k×bmax+11),1≤k≤min(n,256)(3)
二、算法设计复杂度分析(伪代码,不要粘贴源码)

时间复杂度:
T ( n ) ∈ θ ( ∑ i = 1 n min ( i , L m a x ) ) = θ ( L m a x × n ) = θ ( n ) T(n) \in \theta(\sum_{i=1}^{n}{\min{(i, Lmax)}})=\theta(Lmax\times n)=\theta(n) T(n)∈θ(i=1∑nmin(i,Lmax))=θ(Lmax×n)=θ(n)
空间复杂度:
该算法需要辅助空间储存段长、位宽及前 i i i个像素最优压缩占用空间大小, S ( n ) ∈ θ ( n ) S(n)\in \theta(n) S(n)∈θ(n).
三、实验结果记录和分析(测试向量上的测试结果、运行时间)
实验结果:
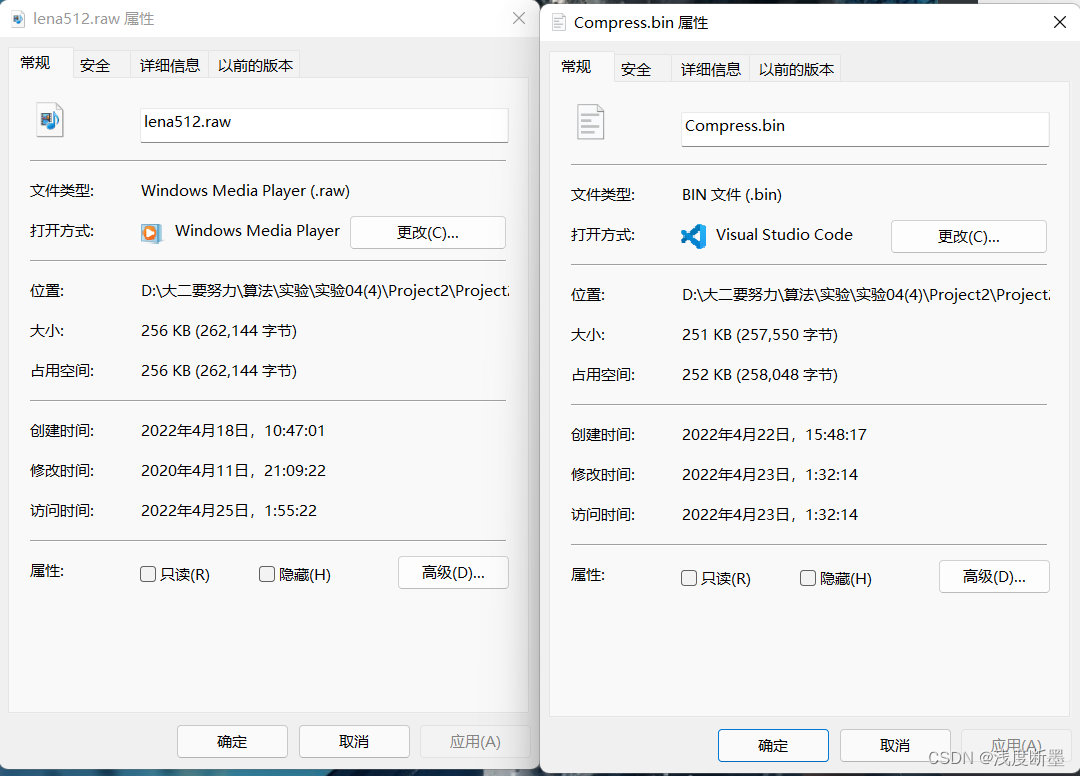
| 原图像大小 | 压缩后大小 |
|---|---|
| 262114字节 | 257550字节 |
压缩率: ( 1 − 257550 262114 ) × 100 % ≈ 1.75 % (1-\frac{257550}{262114} )\times 100\% \approx 1.75\% (1−262114257550)×100%≈1.75%,详见RESULT文件夹
算法运行时间:267.847
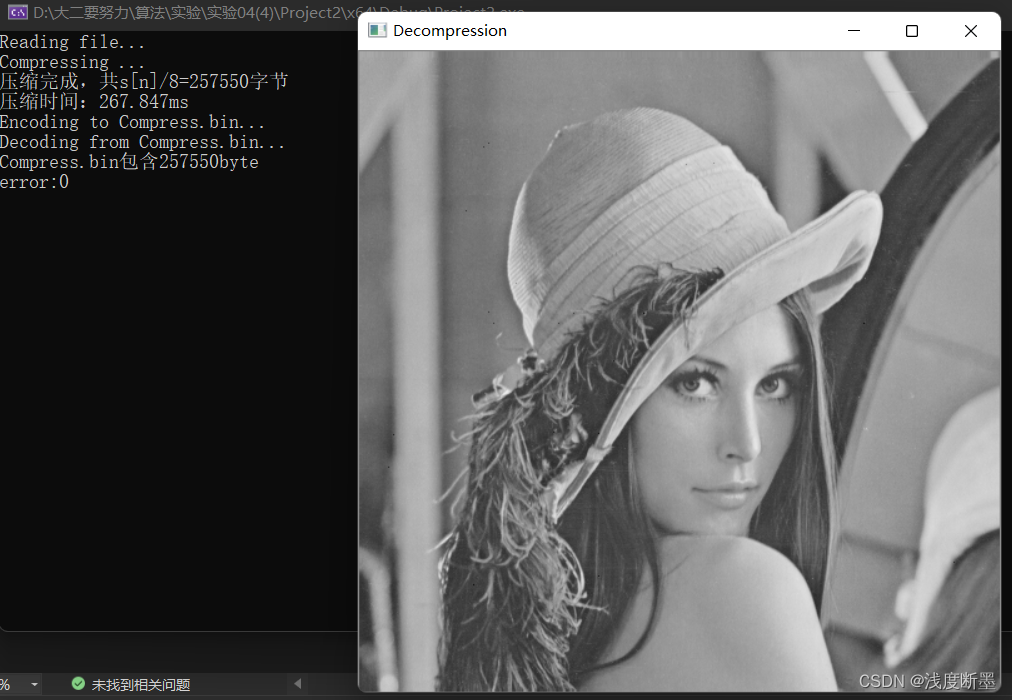
结果验证:
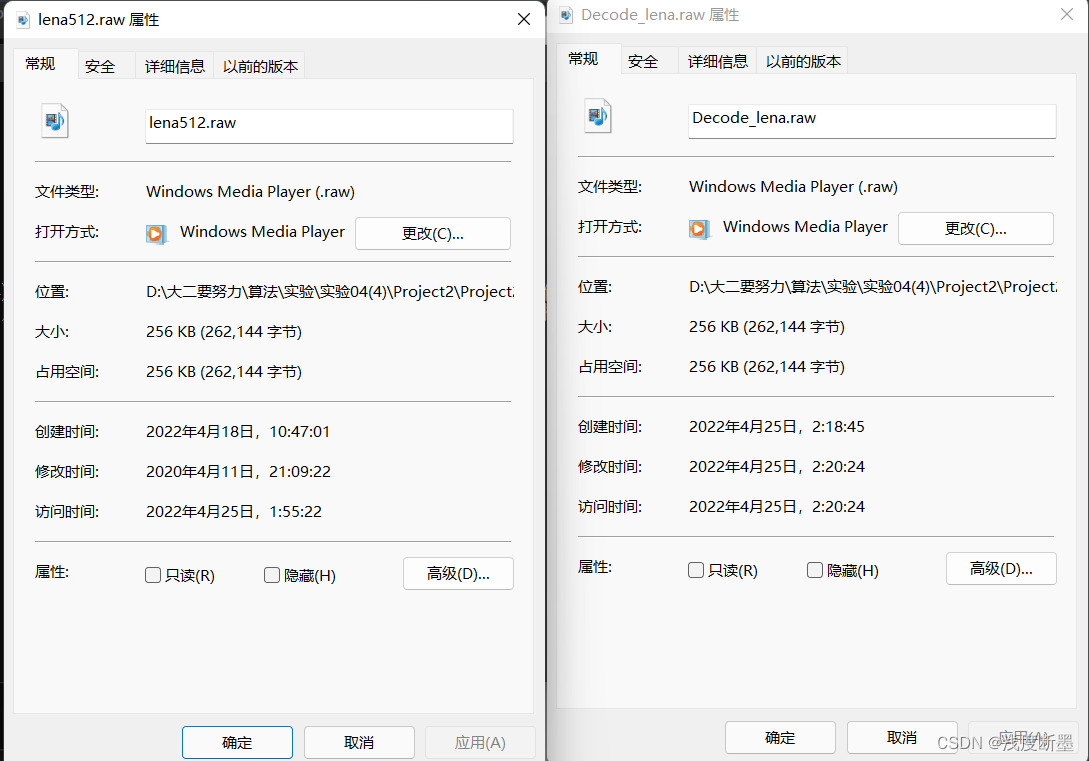
文件大小一致,下使用c++库OpenCV将Decode_lena.raw转存为jpg格式文件,详见RESULT文件夹。
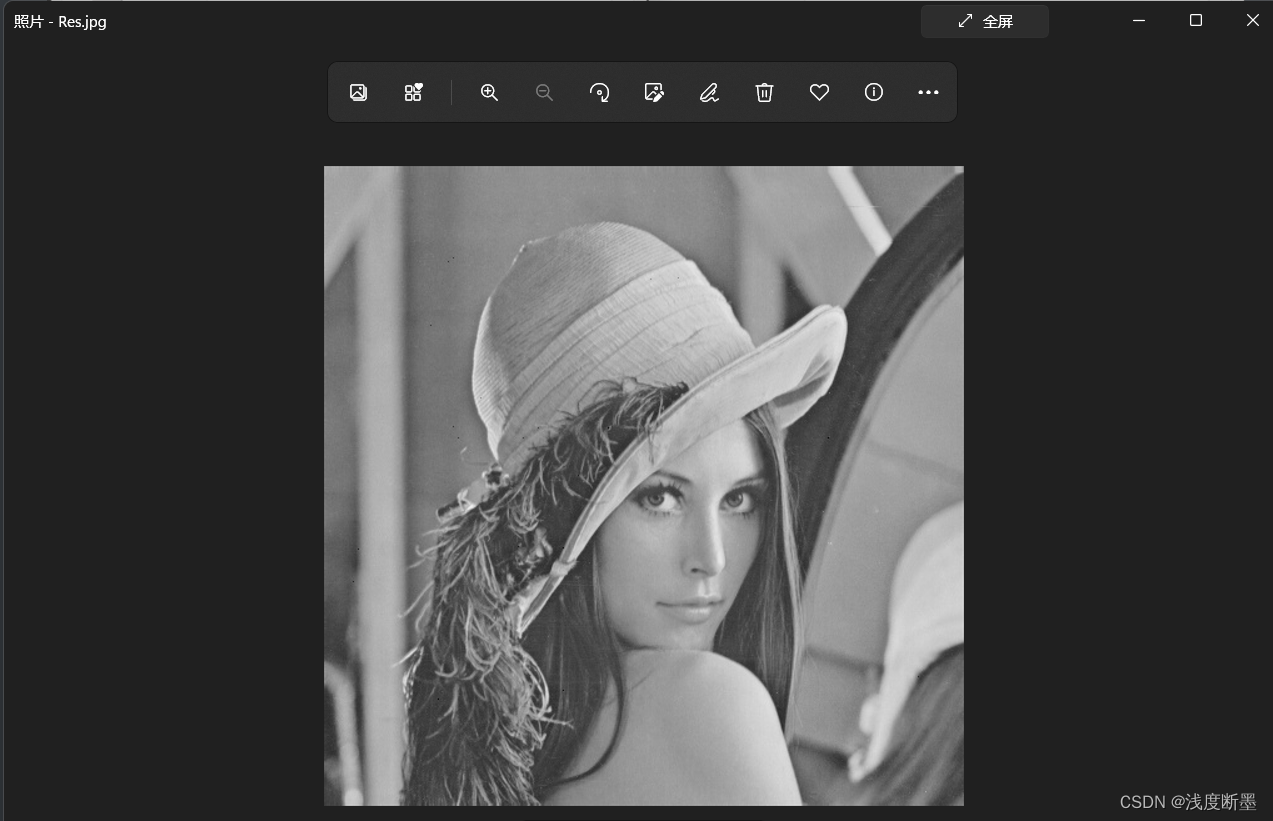
与原图像一致,详见RESULT文件夹。
四、总结(可描述出现的问题和解决方法、经验和反思等)
本实验中采用bin文件格式保存中间编码(压缩)文件以直观显示压缩完成后文件大小,本实验所有代码保存于CODE文件夹,所有结果保存于RESULT文件夹以便老师查阅。
本实验的压缩方式相对单一,压缩率较低,有较大提升空间,具体算法有:
- 将像素值均大于 2 7 = 128 2^7=128 27=128的分段进行取反操作,保存像素值与 256 256 256之差,段长最大值减一,需多加一位符号位表示是否取反,对于像素值较大的图像压缩率较大。
- 对于一段像素值用高斯分布等概率模型拟合,保存参数后解压时用概率分布函数生成像素值。
相关文章:

实验04:图像压缩(DP算法)
1.实验目的: 掌握动态规划算法的基本思想以及用它解决问题的一般技巧。运用所熟悉的编程工具,运用动态规划的思想来求解图像压缩问题。 2.实验内容: 给定一幅图像,求解最佳压缩,使得压缩后的文件最小。 3.实验要求…...

4.19--面试系列之真题版本--redis出现大key怎么解决?Redis 大 Key 对持久化有什么影响?
对于redis出现大key的情况,可以通过以下几种方式来解决: 1.分布式存储:将大key拆分成多个小的key,分别存储在不同的节点上。 2.数据过期:对于大key中不经常使用的数据,可以使用redis自带的过期特性…...

新手在家做自媒体要如何起步?
不少人都想做自媒体来增加自己的收入或者创业,但没有人带领,自己像是无头苍蝇一样,不知道往哪里走。 今天这期内容大周就来给粉丝们分享一点干货,如果对你有所帮助,记得点赞支持一下大周。 1、注册账号 如果你连一个…...

易基因:禾本科植物群落的病毒组丰度/组成与人为管理/植物多样性变化的相关性 | 宏病毒组
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。 现代农业通过简化生态系统、引入新宿主物种和减少作物遗传多样性来影响植物病毒的出现。因此,更好理解农业生态中种植和未种植群落中的病毒分布,以及它们之间的病…...

华为OD机试——对称美学(通过率只有8.51%???)
用java写的这道题,两个样例都可以通过,但是提交之后最终的通过率只有8.51%???自己搞了半天一直都是这个通过率,然后用网上说的100%通过率的代码也是一样的结果,最后时间到了还是没有拿到满分&am…...

【三十天精通Vue 3】第十六天 Vue 3 的虚拟 DOM 原理详解
引言 Vue 3 的虚拟 DOM 是一种用于优化 Vue 应用程序性能的技术。它通过将组件实例转换为虚拟 DOM,并在组件更新时递归地更新虚拟 DOM,以达到高效的渲染性能。在 Vue 3 中,虚拟 DOM 树由 VNode 组成,VNode 是虚拟 DOM 的基本单元…...

Arduino ESP8266通过udp获取时间以及同步本地时间方法
Arduino ESP8266通过udp获取时间以及同步本地时间 ✨通过udp获取NTP服务器上的时间戳,然后经过转换,得到当前具体的时间。转换相对复杂,对于获取时间还是相对比较准确。📝通过udp获取时间实现代码 #include <ESP8266WiFi.h> #include <WiFiUdp.h>//填写 WiFi…...
c/c++:char*定义常量字符串,strcmp()函数,strcpy()函数,寻找指定字符,字符串去空格
c/c:char*定义常量字符串,strcmp()函数,strcpy()函数,寻找指定字符,字符串去空格 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,此时学会c的话, 我所…...

2023年6月DAMA-CDGA/CDGP数据治理认证考试可报名地区公布
2023年4月23日,据DAMA中国官方信息,目前6月DAMA-CDGA/CDGP数据治理认证考试开放报名地区有:北京、上海、广州、深圳、长沙、呼和浩特。目前南京、济南、西安、杭州等地区还在接近开考人数中,打算6月考试的朋友们可以抓紧时间报名啦…...

UDS的0x19服务介绍
什么是 UDS? UEI (Unified Diagnostic Services,统一诊断服务) 是一种在车辆电子控制单元 (ECU) 之间交换诊断信息的标准通信协议,它是OBD-II的某些扩展。利用 UDS 协议,诊断工程师可以访问车辆的各种功能,如读取故障…...
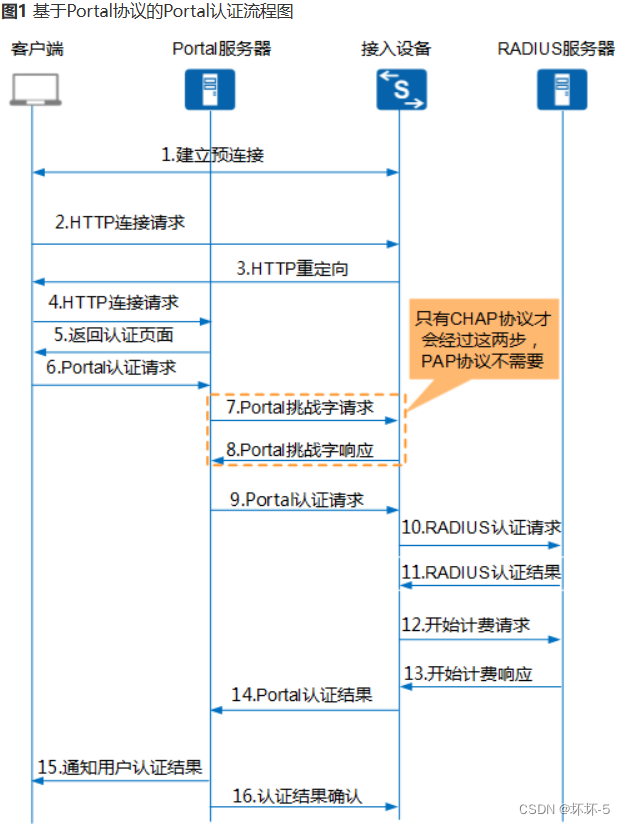
QinQ技术与Portal技术
QinQ 802.1Q-in-802.1Q,是一种扩展VLAN标签技术。在城域网中,需要大量的VLAN来隔离区分不同的用户,但是原有的802.1Q只有12个比特,仅能标识4096个VLANQinQ即在802.1Q的基础上,再增加一层外层标签。使得可以标识4096*40…...
详细使用)
Vue-自定义表单验证(rule,value,callback)详细使用
前言 最近在实际开发中遇到需要验证合同编号是否在数据库已经存在,自定义表单验证。 的表单验证大家都知道form绑定rules,prop绑定值与form.值一样,必填,失去焦点触发 提示信息。 今天我们讲一讲自定义验证规则具体使用场景和它…...

港联证券|TMT板块全线退潮,这些个股获主力逆市抢筹
计算机、电子、传媒、通讯职业流出规模居前。 今天沪深两市主力资金净流出709.92亿元,其中创业板净流出218.36亿元,沪深300成份股净流出187.92亿元。 资金流向上,今天申万一级职业普跌,除了国防军工职业小幅上涨,获主…...
WPF学习
一、了解WPF的框架结构 (第一小节随便看下就可以,简单练习就行) 1、新建WPF项目 xmlns:XML的命名空间 Margin外边距:左上右下 HorizontalAlignment:水平位置 VerticalAlignment:垂直位置 2…...

C#使用WebDriver模拟浏览器操作WEB页面
有时候需要模拟访问页面触发某个功能,可以使用WebDriver来实现这一功能,驱动打开浏览器,并对页面重定向以及对页面写入脚本等操作。 安装Selenium.Chrome,Selenium.Support.UI,Selenium 引入 using OpenQA.Selenium.…...

正则表达式 - 简单模式匹配
目录 一、测试数据 二、简单模式匹配 1. 匹配字面值 2. 匹配数字和非数字字符 3. 匹配单词与非单词字符 4. 匹配空白字符 5. 匹配任意字符 6. 匹配单词边界 7. 匹配零个或多个字符 8. 单行模式与多行模式 一、测试数据 这里所用文本是《学习正则表达式》这本书带的&a…...
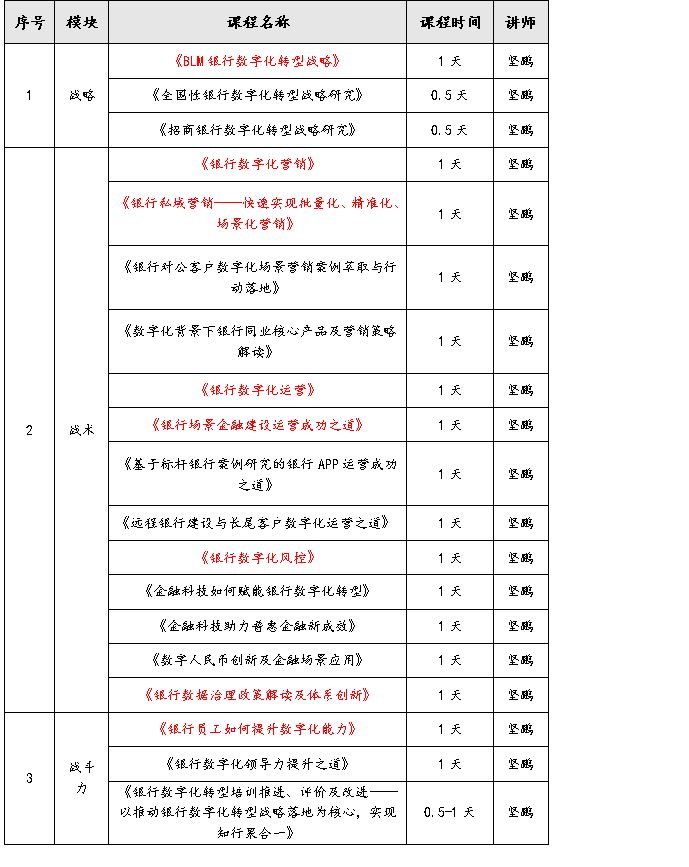
银行数字化转型导师坚鹏:银行数字化转型培训方案
目录 一、银行数字化转型培训背景 二、银行数字化转型模型 三、银行数字化转型课程设计思路 四、 银行数字化转型课程基本介绍 五、 银行数字化转型课程设置 六、银行数字化转型课程大纲 七、培训方案实施流程 一、银行数字化转型培训背景 2020年1月3日ÿ…...
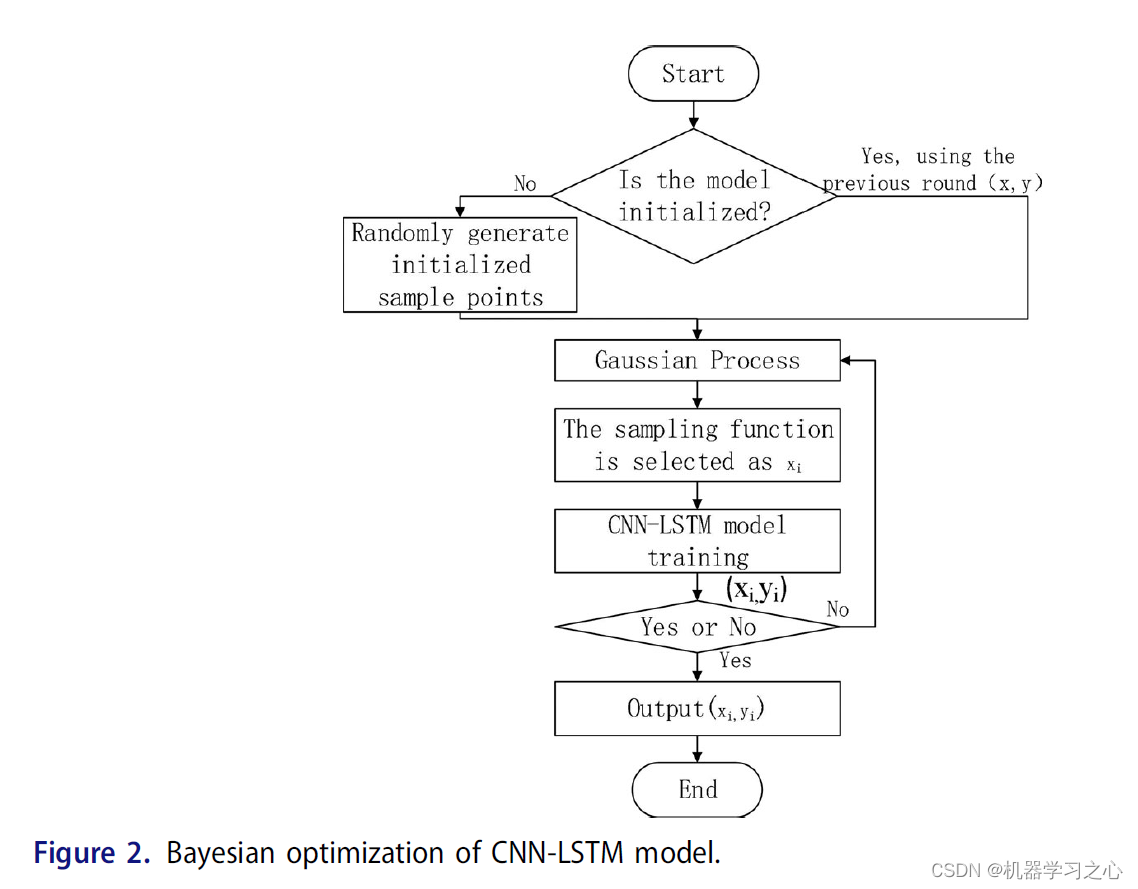
多维时序 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多变量时间序列预测
多维时序 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多变量时间序列预测 目录 多维时序 | MATLAB实现BO-CNN-LSTM贝叶斯优化卷积神经网络-长短期记忆网络多变量时间序列预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 基本介绍 MATLAB实现BO-CNN-…...
)
Shell知识点(一)
1.echo 命令 echo命令的作用是在屏幕输入一行文本,可以降该命令的参数原样输出。 $ echo hello world hello world 如果想要输出的是多行文本,包含换行符,这时就需要把多行文本放在引号里面 $ echo "<HTML><HEAD><TITLE…...

mysql 索引失效、联合索引失效场景和举例
索引失效 假设有一张user 表,表中包含索引 (id); (name); (birthday); (name,age); 对索引字段进行函数操作 select name from user where year(birthday) 2000;使用模糊查询,查询中使用通配符 select name from user where name like %益达%;使用i…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...
