使用bert4keras出现的问题(Process finished with exit code -1073741819 (0xC0000005))
1、环境
python 3.7.12
tensorflow 1.15
keras 2.3.1
bert4keras 0.9.7
protobuf 3.19.0
numpy 1.16.5
2、出现问题
- numpy版本不兼容问题所以你就直接按照我的版本就可以了(numpy 1.16.5)
- Process finished with exit code -1073741819 (0xC0000005) 代码程序直接给我把程序终止了
3、问题分析
首先查阅了资料也看了苏神github博客确实有人遇到了这个问题,但是问题其实并没有解决。无法训练,报错进程已结束,退出代码为 -1073741819 (0xC0000005) · Issue #345 · bojone/bert4keras (github.com)
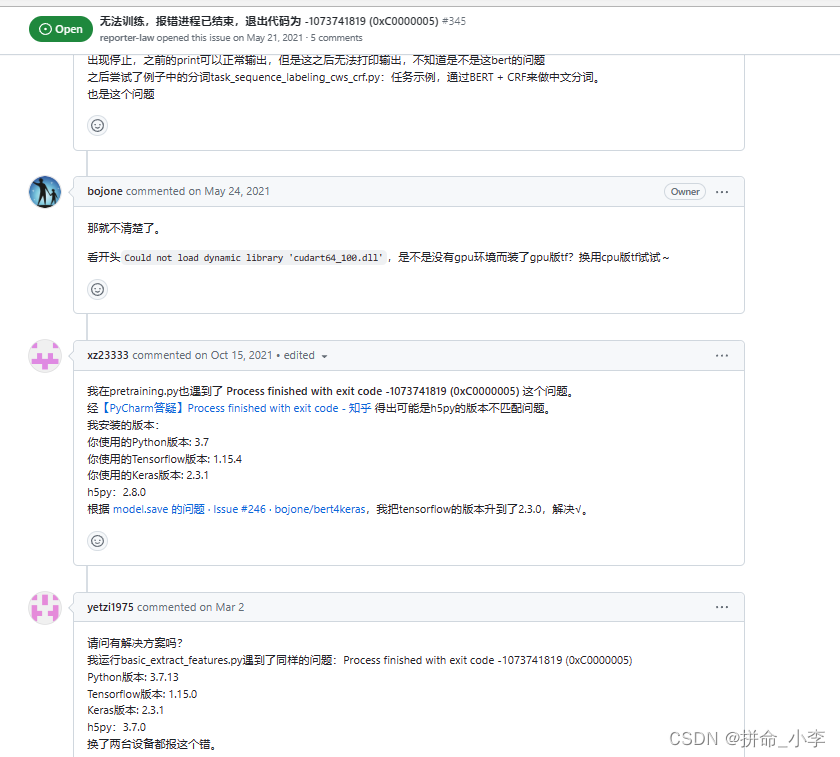
除此之外我查到了一些博客,有下面几种情况,第一种是说需要把模型文件重新保存一下,但我觉得的不太对 我也没去试

还有就是说缺少dll文件,但是我看我的提示里边啥也没有,所以我觉得好像也不是这个原因
 另外一个博客说是对应模型文件路径的问题,需要把路径改为据对路径,我试了一下依然没有什么用处,接着有查阅了很多博客依然没有什么可用的解决办法,所以我想这从代码入手亲自找到这个问题,通过pycahrm的debugger调试我终于知道程序强制退出停止的问题位置,但是依然不知道解决办法,但是至少知道了问题点在哪里问题就等于解决了一半了。就是
另外一个博客说是对应模型文件路径的问题,需要把路径改为据对路径,我试了一下依然没有什么用处,接着有查阅了很多博客依然没有什么可用的解决办法,所以我想这从代码入手亲自找到这个问题,通过pycahrm的debugger调试我终于知道程序强制退出停止的问题位置,但是依然不知道解决办法,但是至少知道了问题点在哪里问题就等于解决了一半了。就是
build_transformer_model方法里边的这一块的问题只要一加载权限文件程序就直接崩溃了,通过定位问题点我又查阅了对应的相关资料博客

终于找到了以为博主的建议,我也是抱着侥幸的心理尝试了一下,果然哈哈哈哈

解决办法如下:(添加tensorflow的引入,然后将其checkpoint文件目录使用tf.train.latest_checkpoint加载进去)
# 添加引入
import tensorflow as tfconfig_path = './model/chinese_L-12_H-768_A-12/bert_config.json'
checkpoint_path = tf.train.latest_checkpoint(r'./model/chinese_L-12_H-768_A-12/bert_model.ckpt')
dict_path = './model/chinese_L-12_H-768_A-12/vocab.txt'以上就是我今日分享的小tips哈哈哈,希望能够帮助到你~
相关文章:

使用bert4keras出现的问题(Process finished with exit code -1073741819 (0xC0000005))
1、环境 python 3.7.12 tensorflow 1.15 keras 2.3.1 bert4keras 0.9.7 protobuf 3.19.0 numpy 1.16.5 2、出现问题 numpy版本不兼容问题所以你就直接按照我的版本就可以了(numpy 1.16.5) Process finished with exit code -1073741819 (0xC0000005) …...
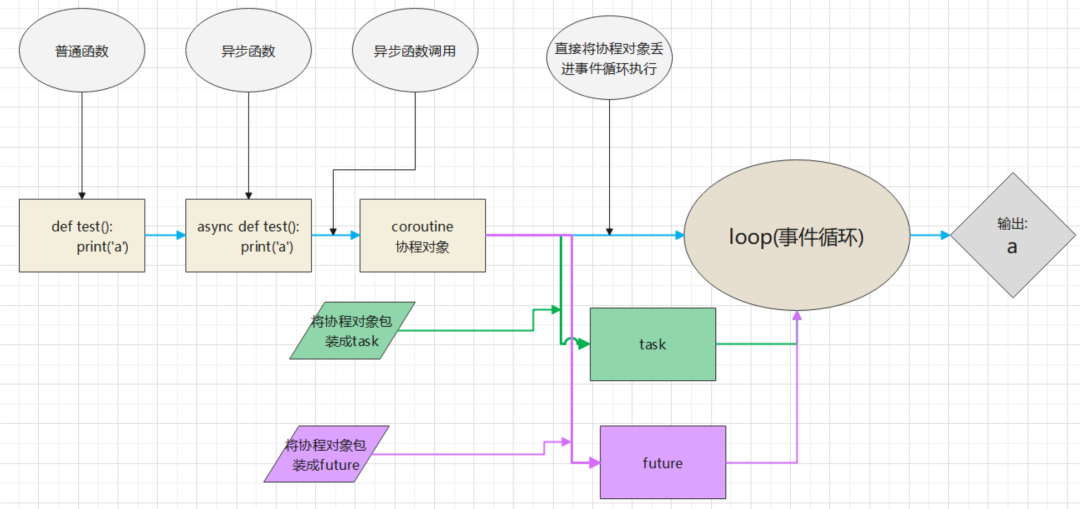
python协程实战
协程简介 协程(Coroutine)又称微线程、纤程,协程不是进程或线程,其执行过程类似于 Python 函数调用,Python 的 asyncio 模块实现的异步IO编程框架中,协程是对使用 async 关键字定义的异步函数的调用; 一个进程包含多个线程,类似…...
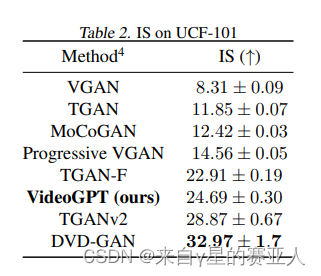
【论文笔记】VideoGPT: Video Generation using VQ-VAE and Transformers
论文标题:VideoGPT: Video Generation using VQ-VAE and Transformers 论文代码:https://wilson1yan. github.io/videogpt/index.html. 论文链接:https://arxiv.org/abs/2104.10157 发表时间: 2021年9月 Abstract 作者提出了…...
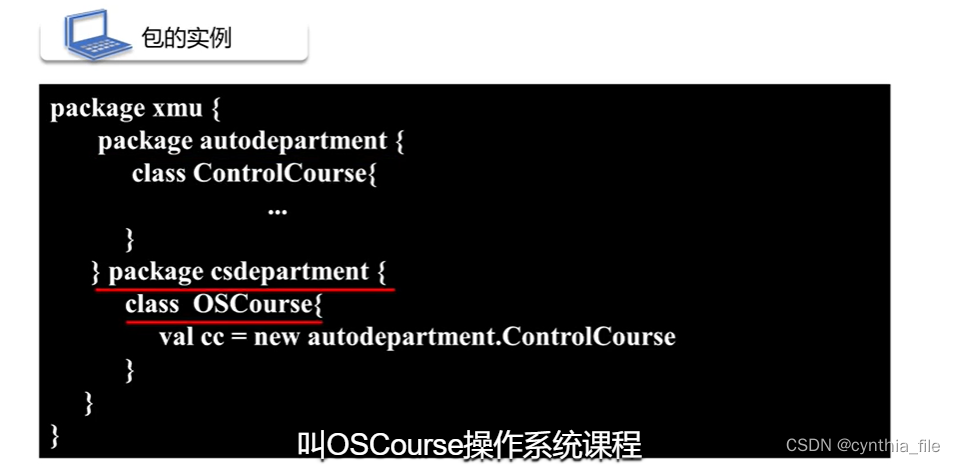
scala之基础面向对象
scala 既是面向对象 也是函数式编程 从Java 发展而来,依赖JVM环境 一、 scala 在linux中运行 scala 模式中直接编写运行 scala文件,load执行 scala编译程序 编译 运行 scala java 二、scala 数据类型 基础数据类型 val 不可变变量 函数式编程 …...

Qt5.12实战之多线程编程概念
1.为什么要使用多线程? a. 基于线程,同时处理多个任务,软件响应更灵敏 b.充分利用CPU的多核心功能增加应用运行效率 c.多线程在同一进程间使用共享通信更加高效 d.多个线程之间进行切换比多个进程之间进行切换,线程开销更少. 2.操作系统与进程关系 a. MS-DOS系统 属于单进程…...
格式化数据恢复怎么做?超实用的3种方法在这!
案例:格式化数据怎么恢复 【我的电脑前段时间中病毒了,无奈之下我只能将其格式化,但是很多重要的文件和图片之类的也一起被删除了,有什么方法可以恢复这些格式化的数据吗?非常着急!】 格式化数据恢复&…...

【Java|golang】1105. 填充书架---动态规划
给定一个数组 books ,其中 books[i] [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。 按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。 先选几本书放在书架上(它们的厚度之和小于等于书架的宽度 shelfWidt…...

linux基础命令
linux基础命令 一、linux命令 熟悉账务linux命令对运维的好处是巨大的,只有熟悉了命令咱们在运维的操作上才能如鱼得水。 系统信息 arch #显示机器的处理器架构(1) uname -m #显示机器的处理器架构(2) uname -r #显示正在使用的内核版本 dmidecode -q …...

【三十天精通Vue 3】 第十八天 Vue 3的国际化详解
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录 引言一、Vue 3 国际化概述1.1 国际化的概念1.2 国际化的作用1.3 V…...

02 - 学会提问
学会提问 一、引言 1.1 GPT简介 GPT(Generative Pre-trained Transformer)是一种基于Transformer架构的大型预训练语言模型。 凭借其强大的文本生成、理解和处理能力,GPT已在诸如自然语言处理、机器翻译、文本摘要等多个领域取得了显著的…...

Java经典的Main方法面试题
mian方法是做什么用的? main方法是Java程序的入口方法,JVM在运行的时候会首先查找main方法不用main方法如何运行一个类? 不行,没有main方法我们不能运行Java类 在Java7之前,你可以通过使用静态初始化运行Java类。但是&…...

世界大学电子电气工程TOP10,国内大学哪家强?
EE究竟是什么专业 ? 在中国,工程系中跟电相关的专业,一般都切分得非常细。有电子工程、电气工程、通信工程、信息工程、自动化、测控仪器等。但在国外,一般把这些领域都归类到 Electrical Engineering 中,也就是我们常说的EE。 …...

5.3 牛顿-科茨公式
学习目标: 理解微积分基础知识,例如导数和微分的概念。学习牛顿-科茨公式的推导过程。这个公式实际上是使用泰勒公式对被积函数进行展开,并使用微积分的基本原理进行简化得到的。学习如何使用牛顿-科茨公式进行数值积分。这通常涉及到将被积…...

全注解下的SpringIoc 续2-bean的生命周期
spring中bean的生命周期 上一个小节梳理了一下Spring Boot的依赖注入的基本知识,今天来梳理一下spring中bean的生命周期。 下面,让我们一起看看bean在IOC容器中是怎么被创建和销毁的。 bean的生命周期大致分为四个部分: #mermaid-svg-GFXNEU…...

【VQ-VAE代码实战】Neural Discrete Representation Learning
【VQ-VAE代码实战】Neural Discrete Representation Learning 0、前言1、简介2、Basic IdeaLoss3、代码Load DataVector Quantizer LayerEncoder & Decoder ArchitectureTrainPlot LossView ReconstructionsView EmbeddingReference0、前言 论文地址:基于神经网络的,离散…...
gpt3.5和gpt4区别-gpt3.5和gpt4
gpt系列 GPT系列是OpenAI公司开发的一组基于人工智能深度学习技术的自然语言处理模型。GPT代表Generative Pre-trained Transformer,即预训练生成模型。目前,GPT模型已经推出了三代(GPT-1,GPT-2,GPT-3)&am…...

java获取当前系统时间
在Java中,可以使用以下几种方法获取当前系统时间: 方法1:使用java.util.Date类 java import java.util.Date; public class Main { public static void main(String[] args) { Date date new Date(); System.out.println("当前时间&…...
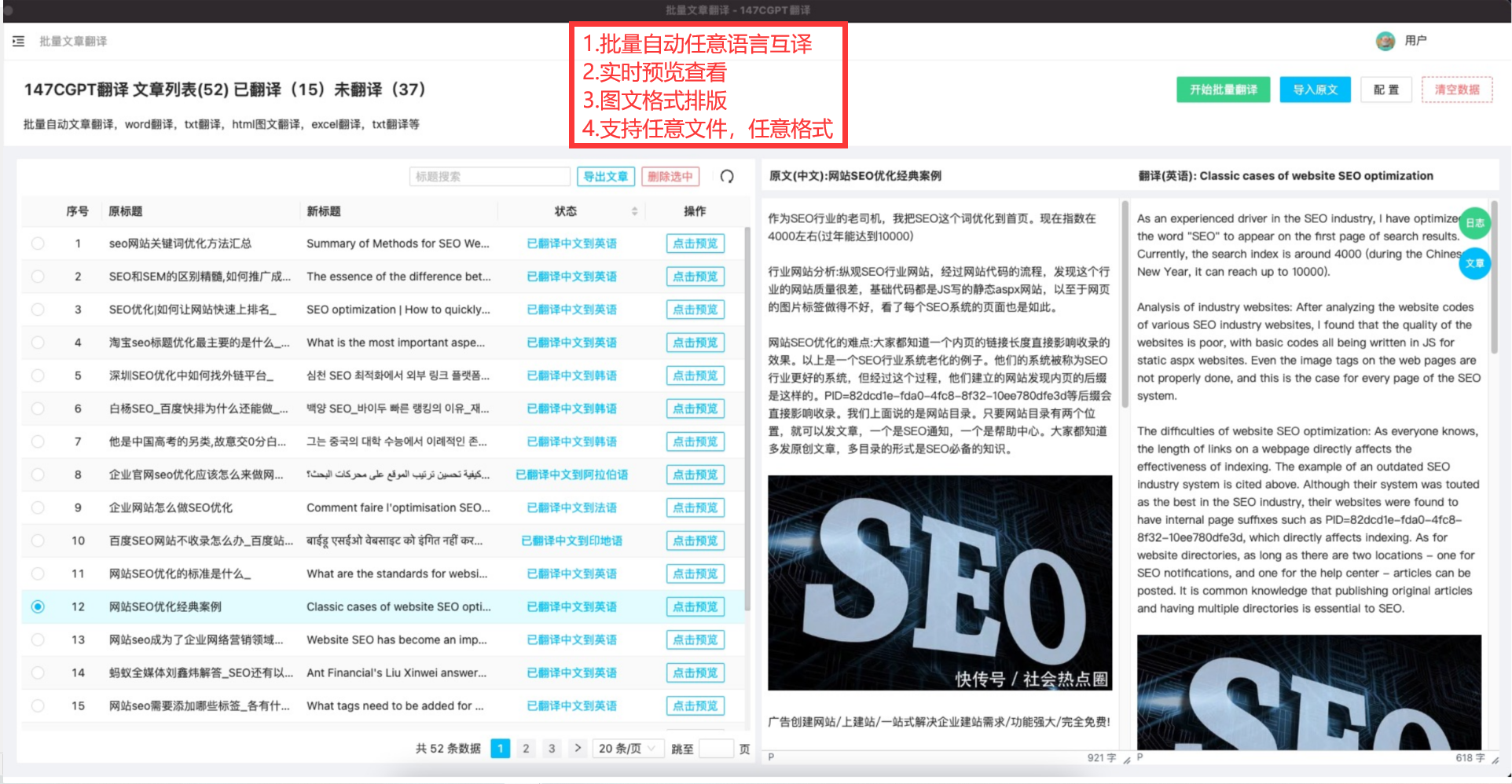
pbootcms自动配图出图插件
pbootcms文章无图自动出图配图插件的优点 1、提高文章的可读性和吸引力:插入图片可以丰富文章的内容和形式,增强读者的阅读体验和吸引力,提高文章的点击率和转化率。 2、节省时间和精力:手动添加图片需要花费大量时间和精力去寻找…...
手动测试台架搭建,让你的车载测试更轻松
目录:导读 引言 1、概述 2、主要内容 3、汽车测试台架分类 4、汽车测试台架分类 5、汽车测试台架分类台架测试输人台架硬件搭建CANoe台架搭建 6、台架测试输入? 7、需求规范是功能测试用例设计来源测试结果的判断﹔包括∶客户需求(功能规范)需求分…...
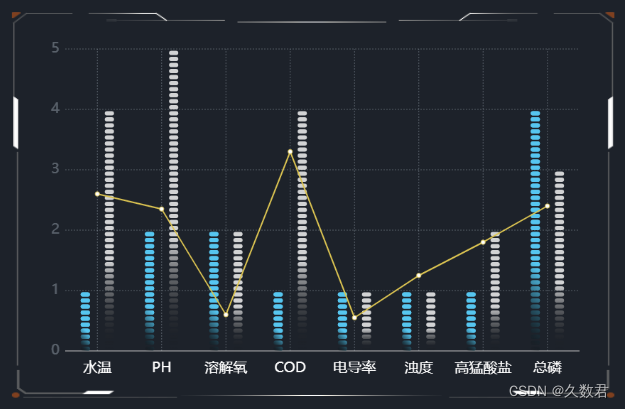
分组双轴图:揭示数据中的关联性和趋势变化
简介 分组双轴图是一种数据可视化图表,指有多个(≥2)Y轴的数据图表,多为分组柱状图折线图的结合,图表显示更为直观,可以很好地展示不同指标之间的关系,帮助用户更好地理解数据,做出…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
