5.3 牛顿-科茨公式
学习目标:
- 理解微积分基础知识,例如导数和微分的概念。
- 学习牛顿-科茨公式的推导过程。这个公式实际上是使用泰勒公式对被积函数进行展开,并使用微积分的基本原理进行简化得到的。
- 学习如何使用牛顿-科茨公式进行数值积分。这通常涉及到将被积函数替换为一个多项式,然后对多项式进行积分。
- 学习牛顿-科茨公式的应用,例如在数值微积分和数值求解微分方程中的应用。

5.3.1 牛顿-科茨公式
牛顿-科茨公式是一种数值积分公式,用于计算定积分的近似值。它基于在积分区间上采用等距节点的插值多项式,通过将多项式积分来近似定积分的值。
牛顿-科茨公式的一般形式为:
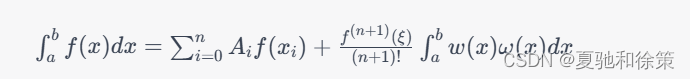
其中,a和b是积分区间的端点,f(x)是被积函数,n是插值多项式的次数,x_i是区间上的等距节点,\xi是一个介于a和b之间的常数,A_i是插值多项式中x^i项的系数,w(x)是一个权重函数,\omega(x)是插值多项式的基函数。
牛顿-科茨公式的一个优点是可以根据需要选择合适的插值多项式次数$n$,以平衡精度和计算复杂度。此外,它也可以通过将积分区间分成若干个小区间,然后分别使用公式来计算每个小区间上的积分,从而提高精度。
牛顿-科茨公式的主要难点在于确定权重函数$w(x)$和基函数$\omega(x)$,这涉及到一些数学推导和技巧。此外,还需要注意插值多项式次数的选择、积分区间的选取和节点数的确定等问题,以确保计算精度和计算效率。

我的理解:
牛顿-科茨公式是一种利用函数在某一点处的导数信息,通过不断递推使用差商来逼近函数值的方法。它将函数的数值逼近问题转化为求解差商的问题,可以通过递推的方式快速求解多项式的系数。这种方法的优点是计算效率高、精度较高,可以用于求解各种数学问题,如求解方程、计算数值积分等。其基本思想是在已知一些函数值和对应的导数值的前提下,利用递推公式不断求出差商,最终逼近目标函数的值。
 辛普森公式:
辛普森公式:
辛普森公式是一种数值积分方法,用于计算给定函数的定积分。它是基于二次多项式插值的思想,将被积函数在区间 $[a,b]$ 上划分为若干个小区间,每个小区间上采用二次多项式插值公式,最终得到整个区间的积分值。
具体地,辛普森公式是将被积函数 $f(x)$ 在区间 $[a,b]$ 上分成若干个小区间,每个小区间采用二次多项式插值公式:

其中 $x_i=a+ih_i$,$i=0,1,\ldots,n$,$h_i=\frac{b-a}{2n}$。
然后,对于每个小区间 $[x_i,x_{i+2}]$,将其积分值计算为:
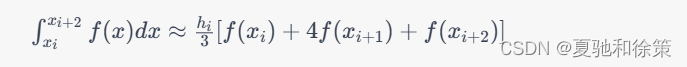
最终将所有小区间的积分值相加,即可得到整个区间 $[a,b]$ 的积分值。
辛普森公式的精度很高,其代数精度为 $2$ 阶,即在 $[a,b]$ 上任意次可微的函数 $f(x)$,用辛普森公式计算积分的误差为:
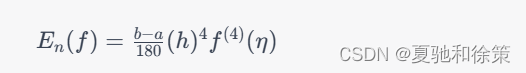
其中 $h=\frac{b-a}{2n}$,$\eta\in [a,b]$。
需要注意的是,辛普森公式的使用需要将区间 $[a,b]$ 平均分成偶数份。如果区间不能平均分割,则需要使用其他数值积分方法。

我的理解:
辛普森公式是数值积分中的一种常用方法,可以用于计算一定区间上函数的定积分。其基本思想是将被积函数在区间上用二次多项式拟合,再对其进行积分。其公式为:
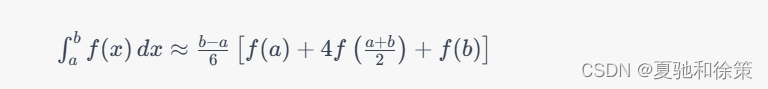
其中 $f(x)$ 是被积函数,$a$ 和 $b$ 是积分区间的端点。公式右边是被积函数在区间 $[a,b]$ 上按照一定权重进行采样的结果。可以看出,辛普森公式是基于两个区间上的梯形公式和中点公式相加而得到的。
辛普森公式的精度比梯形公式和中点公式都要高,其误差项的阶数为 $O(h^4)$,这意味着辛普森公式的误差随着步长的减小而更快地逼近零。因此,在需要较高精度的数值积分计算中,辛普森公式是一种很好的选择。
 3.2 复合低阶牛顿-科茨公式
3.2 复合低阶牛顿-科茨公式
复合低阶牛顿-科茨公式是一种用于数值积分的方法,它是在牛顿-科茨公式的基础上进一步推广和优化而来的。与牛顿-科茨公式相比,复合低阶牛顿-科茨公式可以处理更加复杂的积分问题,并且能够在保证精度的同时大幅减少计算量。
其基本思想是将积分区间 [a,b]分成 n个小区间,然后在每个小区间上使用低阶牛顿-科茨公式进行数值积分,最后将每个小区间的积分结果相加即可得到整个积分区间 [a,b]的积分近似值。
具体来说,设 h = \frac{b-a}{n}为小区间长度,则将积分区间 $[a,b]$ 均分成 $n$ 个小区间 [x_i,x_{i+1}],其中 x_i=a+ih,$i=0,1,\cdots,n-1$。然后在每个小区间上采用低阶牛顿-科茨公式进行数值积分,设第 $i$ 个小区间上的积分近似值为 $S_i$,则整个积分区间 $[a,b]$ 的积分近似值为:
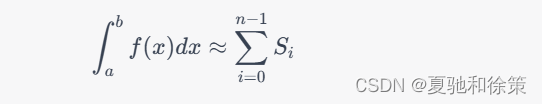
常用的复合低阶牛顿-科茨公式有梯形公式和 Simpson 公式。其中,梯形公式使用线性插值多项式,积分精度为 $O(h^2)$;Simpson 公式使用二次插值多项式,积分精度为 $O(h^4)$。这两个公式的具体形式如下:
梯形公式:

Simpson 公式:
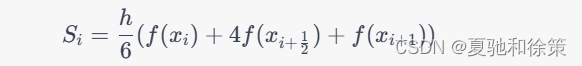
其中 $x_{i+\frac{1}{2}} = \frac{x_i+x_{i+1}}{2}$。需要注意的是,梯形公式和 Simpson 公式的计算要求 $n$ 为偶数,否则需要对积分区间进行适当调整,以保证计算的正确性。
 我的理解:
我的理解:
复合低阶牛顿-科茨公式是一种数值积分方法,其基本思想是将一个区间分割成多个子区间,然后在每个子区间内使用低阶牛顿-科茨公式来逼近函数在该子区间内的积分值,再将所有子区间内的积分值加起来得到整个区间的积分值。这种方法的优点是可以将一个大区间的积分计算拆分成多个小区间的积分计算,从而提高计算精度和效率。
具体而言,复合低阶牛顿-科茨公式通常包括以下几个步骤:
-
将一个大区间[a,b]分割成n个子区间,每个子区间的长度为h=(b-a)/n。
-
对于每个子区间,使用低阶牛顿-科茨公式来逼近函数在该子区间内的积分值。
-
将所有子区间内的积分值加起来,得到整个区间[a,b]的积分值。
-
可以通过改变子区间的数量n来控制计算精度,通常情况下n越大,精度越高,但计算量也越大。
需要注意的是,在实际计算中还需要考虑积分公式的误差和收敛性,以及如何选择合适的分割方式和子区间数量等问题。
 5.3.3 误差的事后估计与步长的自动调整
5.3.3 误差的事后估计与步长的自动调整
在数值积分中,我们通常通过选择合适的数值积分公式和步长来计算积分。然而,在实际计算中,由于积分函数的性质复杂、步长的选取不合理等原因,计算结果可能会产生误差。因此,我们需要对计算结果进行误差估计,并在需要的情况下自动调整步长,以达到所需的精度要求。
误差的事后估计是指在计算完积分后,通过某种方法估计计算结果的误差。一般来说,误差的估计与所采用的数值积分公式以及步长有关。常见的误差估计方法包括以下几种:
-
梯形公式误差估计:基于梯形公式的误差估计公式为$E_t = \frac{h^2}{12}(b-a)f''(\xi)$,其中$h=b-a$是步长,$f''(\xi)$是积分函数在区间$[a,b]$内的二阶导数。
-
辛普森公式误差估计:基于辛普森公式的误差估计公式为$E_s = \frac{h^4}{180}(b-a)f^{(4)}(\xi)$,其中$h=\frac{b-a}{2}$是步长,$f^{(4)}(\xi)$是积分函数在区间$[a,b]$内的四阶导数。
-
复合梯形公式误差估计:基于复合梯形公式的误差估计公式为$E_t = -\frac{h^3}{12n^2}(b-a)f''(\xi)$,其中$h=\frac{b-a}{n}$是步长,$n$是分割区间的个数,$f''(\xi)$是积分函数在区间$[a,b]$内的二阶导数。
-
复合辛普森公式误差估计:基于复合辛普森公式的误差估计公式为$E_s = -\frac{h^5}{2880n^4}(b-a)f^{(4)}(\xi)$,其中$h=\frac{b-a}{2n}$是步长,$n$是分割区间的个数,$f^{(4)}(\xi)$是积分函数在区间$[a,b]$内的四阶导数。
步长的自动调整是指根据当前积分结果和误差估计,自动调整步长以达到所需的精度要求。常见的步长自动调整方法包括以下几种:
- 双精度实数运算:将数值积分的结果存储为双精度实数,然后根据前后两次积分结果的差值进行步长的自适应调整
 我的理解:
我的理解:
误差的事后估计与步长的自动调整是数值积分中常用的优化方法,用于提高数值积分的精度和效率。
在数值积分中,我们通常采用数值积分公式来逼近原函数的积分值。但是,由于数值计算时涉及到舍入误差和截断误差等各种误差,因此我们需要对数值积分的误差进行估计,以便评估数值积分的精度。一般来说,误差的大小取决于数值积分公式的精度和计算步长。
对于误差的事后估计,我们可以通过将不同步长得到的数值积分结果进行比较,进而得到误差估计值。一般来说,我们会选择一些适当的步长序列,例如等距序列或者指数序列,以保证误差估计的准确性和可靠性。
在步长的自动调整中,我们通常会根据当前的误差估计值来调整计算步长,从而达到提高数值积分精度和效率的目的。常见的自动调整方法包括逐步加倍法和Richardson外推法等。
需要注意的是,在应用误差的事后估计和步长的自动调整时,我们需要充分考虑数值积分公式的特点,例如公式的代数精度、收敛性和稳定性等。
 5.3.4 变步长复合梯形法的递推算式
5.3.4 变步长复合梯形法的递推算式
变步长复合梯形法是一种数值积分方法,用于计算定积分的近似值。它是由梯形法和复合梯形法结合而成的方法,采用自适应步长的方式来提高精度。
其递推公式如下:
首先,我们将积分区间[a,b]分成n个子区间,每个子区间的长度为h。则梯形公式的近似积分为:
$I_1=\frac{h}{2}(f(a)+f(b))$
接下来,我们将整个区间[a,b]分成2n个子区间,每个子区间的长度为h/2。则复合梯形公式的近似积分为:
$I_2=\frac{h}{4}(f(a)+2\sum_{i=1}^{n-1}f(a+ih)+2\sum_{i=1}^nf(a+ih)+f(b))$
为了提高精度,我们可以将两次计算的结果进行比较。如果两次计算的误差小于指定的容限,我们就认为计算结果是可靠的,否则就需要将区间进一步细分,重新进行计算。
设第k次计算的近似积分为$I_k$,第k+1次计算的近似积分为$I_{k+1}$,则可以使用以下递推公式:
$I_{k+1}=\frac{1}{2}I_k+\frac{h_k}{2}\sum_{i=1}^{2^k}f(a+(i-\frac{1}{2})h_k)$
其中,$h_k=\frac{b-a}{2^k}$,表示第k次计算的子区间长度。
这个递推公式的意义是将区间[a,b]等分成2^(k+1)个子区间,然后用梯形公式在每个子区间上进行计算,最后将计算结果求和得到第k+1次的近似积分$I_{k+1}$。这样,在每次计算中都会自适应地调整步长,从而提高计算精度。
 我的理解:
我的理解:
变步长复合梯形法是一种数值积分方法,用于计算定积分的近似值。其基本思想是将定积分区间分割成若干个小区间,然后在每个小区间上采用梯形公式进行近似计算,最后将各小区间上的近似值相加得到总近似值。
与传统的复合梯形法不同的是,变步长复合梯形法采用自适应步长策略,即通过控制每个小区间上的步长大小,来达到提高数值积分精度的目的。算法会先计算出一个较大步长下的近似值,然后将整个区间分割成两个小区间,分别在每个小区间上计算近似值。如果两个小区间上的近似值与较大步长下的近似值差异较大,则需要进一步细分区间,重新计算近似值,直至达到预设精度要求。
变步长复合梯形法的递推算式如下:
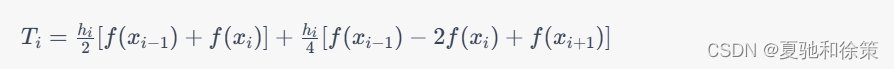
其中,$T_i$表示第$i$个小区间上的近似值,$h_i$表示第$i$个小区间的步长,$f(x_i)$表示被积函数在$x_i$处的函数值。通过递归计算,可以得到总的近似值。
变步长复合梯形法的优点在于能够根据误差大小自适应地调整步长,从而达到更高的数值积分精度。同时,它也可以有效地处理被积函数在某些点处出现突变的情况,因为在这些点处,算法会自动细分小区间,从而保证积分的准确性。

总结:
下面是关于牛顿-科茨公式的重点、难点和易错点的总结:
重点:
- 牛顿-科茨公式是数值积分中的一种常见方法,用于计算定积分近似值。
- 牛顿-科茨公式是基于插值多项式的方法,通过选取若干个等距节点和对应的函数值,构造出一个多项式函数,然后利用该多项式函数来估计定积分值。
- 牛顿-科茨公式有多个版本,包括低阶公式、高阶公式和复合公式,具体使用哪个版本取决于所求定积分的精度要求和计算效率的要求。
- 牛顿-科茨公式的误差通常使用余项来估计,余项的大小与被积函数的光滑性、节点的选取方式、插值多项式的次数等因素有关。
- 变步长复合梯形法是一种常用的自适应积分方法,它通过动态调整步长和计算误差来提高数值积分的精度。
难点:
- 牛顿-科茨公式的精度和效率需要根据具体问题进行权衡和选择,需要有一定的经验和实践。
- 牛顿-科茨公式的余项的推导和分析需要一定的数学基础和技巧,需要熟练掌握多项式插值和微积分的知识。
- 变步长复合梯形法的递推算式比较复杂,需要仔细理解其中的各个参数和变量的含义,以及它们之间的关系。
易错点:
- 节点的选取和多项式的次数对牛顿-科茨公式的精度和效率有重要影响,需要注意选择合适的参数。
- 牛顿-科茨公式的余项计算可能存在一些技巧性问题,需要注意细节。
- 变步长复合梯形法在实现时需要注意边界情况和特殊情况的处理,以及参数的选择和调整。

相关文章:

5.3 牛顿-科茨公式
学习目标: 理解微积分基础知识,例如导数和微分的概念。学习牛顿-科茨公式的推导过程。这个公式实际上是使用泰勒公式对被积函数进行展开,并使用微积分的基本原理进行简化得到的。学习如何使用牛顿-科茨公式进行数值积分。这通常涉及到将被积…...

全注解下的SpringIoc 续2-bean的生命周期
spring中bean的生命周期 上一个小节梳理了一下Spring Boot的依赖注入的基本知识,今天来梳理一下spring中bean的生命周期。 下面,让我们一起看看bean在IOC容器中是怎么被创建和销毁的。 bean的生命周期大致分为四个部分: #mermaid-svg-GFXNEU…...

【VQ-VAE代码实战】Neural Discrete Representation Learning
【VQ-VAE代码实战】Neural Discrete Representation Learning 0、前言1、简介2、Basic IdeaLoss3、代码Load DataVector Quantizer LayerEncoder & Decoder ArchitectureTrainPlot LossView ReconstructionsView EmbeddingReference0、前言 论文地址:基于神经网络的,离散…...
gpt3.5和gpt4区别-gpt3.5和gpt4
gpt系列 GPT系列是OpenAI公司开发的一组基于人工智能深度学习技术的自然语言处理模型。GPT代表Generative Pre-trained Transformer,即预训练生成模型。目前,GPT模型已经推出了三代(GPT-1,GPT-2,GPT-3)&am…...

java获取当前系统时间
在Java中,可以使用以下几种方法获取当前系统时间: 方法1:使用java.util.Date类 java import java.util.Date; public class Main { public static void main(String[] args) { Date date new Date(); System.out.println("当前时间&…...
pbootcms自动配图出图插件
pbootcms文章无图自动出图配图插件的优点 1、提高文章的可读性和吸引力:插入图片可以丰富文章的内容和形式,增强读者的阅读体验和吸引力,提高文章的点击率和转化率。 2、节省时间和精力:手动添加图片需要花费大量时间和精力去寻找…...
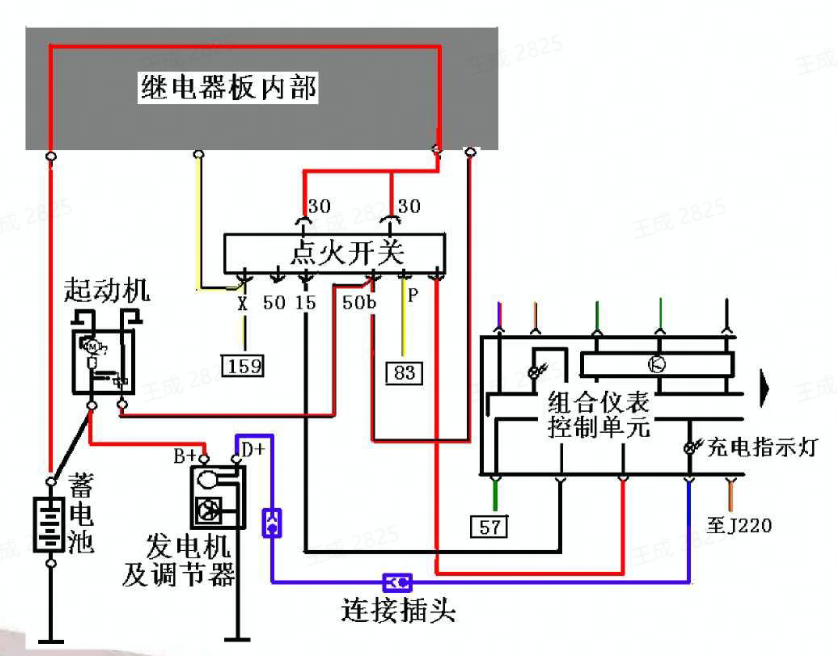
手动测试台架搭建,让你的车载测试更轻松
目录:导读 引言 1、概述 2、主要内容 3、汽车测试台架分类 4、汽车测试台架分类 5、汽车测试台架分类台架测试输人台架硬件搭建CANoe台架搭建 6、台架测试输入? 7、需求规范是功能测试用例设计来源测试结果的判断﹔包括∶客户需求(功能规范)需求分…...
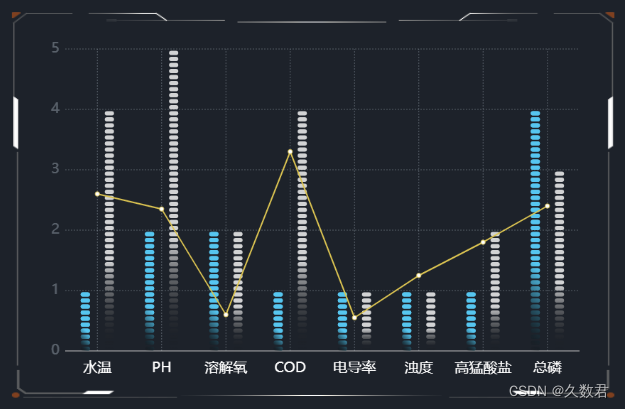
分组双轴图:揭示数据中的关联性和趋势变化
简介 分组双轴图是一种数据可视化图表,指有多个(≥2)Y轴的数据图表,多为分组柱状图折线图的结合,图表显示更为直观,可以很好地展示不同指标之间的关系,帮助用户更好地理解数据,做出…...

MATLAB函数封装1:生成QT可以调用的.dll动态链接库
在进行相关算法的开发和设计过程中,MATLAB具有特别的优势,尤其是对于矩阵运算的处理,具有很多现成的方法和函数可以进行调用,同时MATLAB支持把函数封装成不同的语言方便完成算法的集成。 这里记录利用MATLAB封装成C动态链接库&…...

【算法题】2400. 恰好移动 k 步到达某一位置的方法数目
题目: 给你两个 正 整数 startPos 和 endPos 。最初,你站在 无限 数轴上位置 startPos 处。在一步移动中,你可以向左或者向右移动一个位置。 给你一个正整数 k ,返回从 startPos 出发、恰好 移动 k 步并到达 endPos 的 不同 方法…...
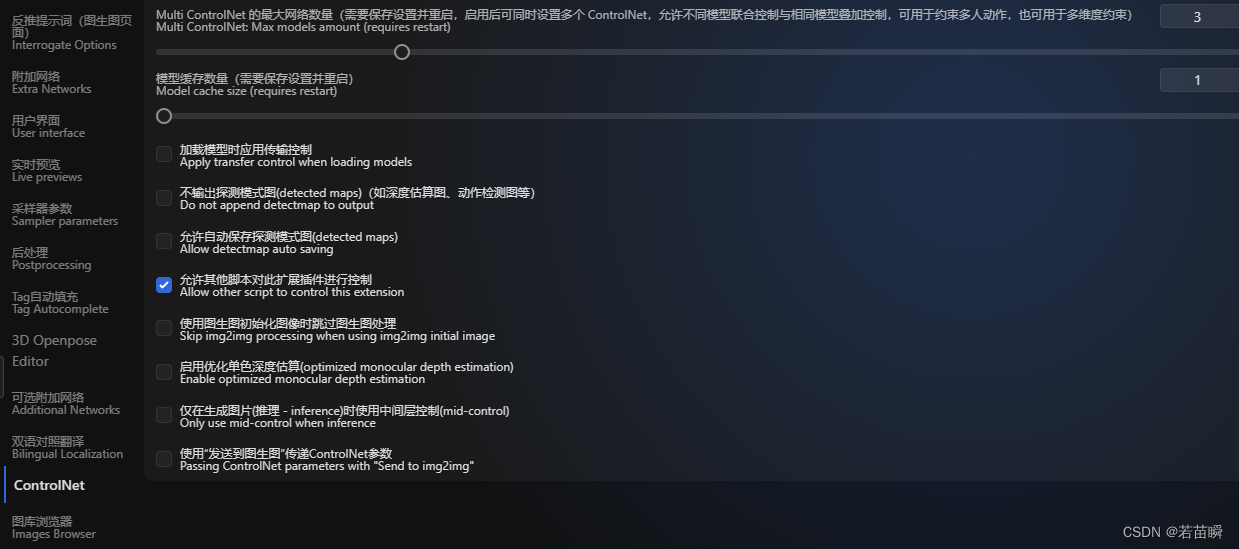
探索【Stable-Diffusion WEBUI】的插件:骨骼姿态(OpenPose)
文章目录 (零)前言(一)骨骼姿态(OpenPose)系列插件(二)插件:PoseX(三)插件:Depth Lib(四)插件:3D …...

MySQL数据落盘原理(redo、undo、binlog、2PC、double write等。)
文章目录 前言一、架构图1、MySQL架构图2、InnoDB架构图 二、落盘分析1.第一阶段2.第二阶段3.第三阶段4.第四阶段5.第五阶段6.第六阶段 三、总结 前言 在上一章中我们聊到了事务有四大特性:原子性、一致性、隔离性、持久性。本篇文章就持久性重点聊一下,…...

智加科技+舍弗勒,首发量产正向开发的智能重卡冗余转向
对于自动驾驶赛道来说,感知、规划和控制,除了计算平台、算法等核心上层软硬件支持,底盘控制系统同样是关键一环。事实上,从Demo到规模化量产,更好的车身控制能力以及冗余备份,也是自动驾驶公司迈入2.0阶段的…...

C++类的模拟实现
📟作者主页:慢热的陕西人 🌴专栏链接:C 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 本博客主要内容讲解了简单模拟实现string类 C类的模拟实现 文章目录 C类的…...

耐腐蚀高速电动针阀在半导体硅片清洗机化学药液流量控制中的应用
摘要:化学药液流量的精密控制是半导体湿法清洗工艺中的一项关键技术,流量控制要求所用调节针阀一是开度电动可调、二是具有不同的口径型号、三是高的响应速度,四是具有很好的耐腐蚀性,这些都是目前提升半导体清洗设备性能需要解决…...
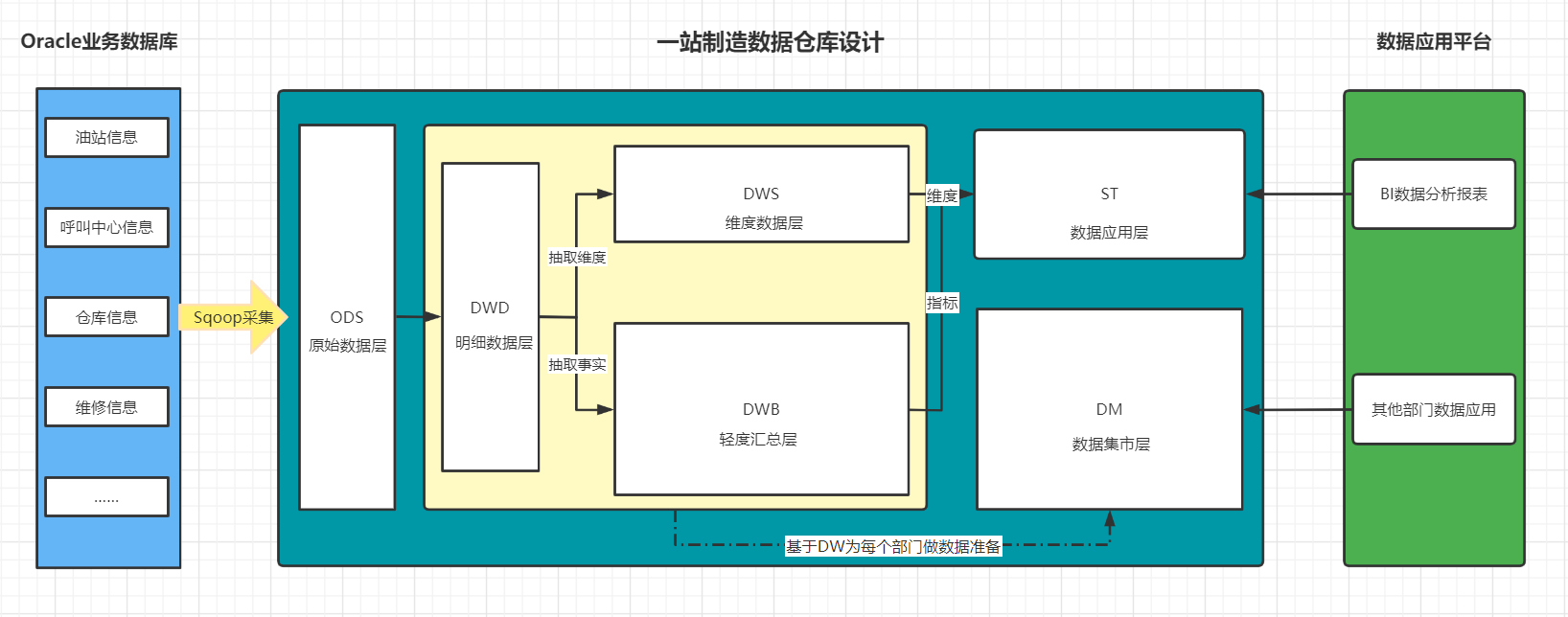
助力工业物联网,工业大数据之ODS层及DWD层建表语法【七】
文章目录 ODS层及DWD层构建01:课程回顾02:课程目标03:数仓分层回顾04:Hive建表语法05:Avro建表语法 ODS层及DWD层构建 01:课程回顾 一站制造项目的数仓设计为几层以及每一层的功能是什么? ODS&…...
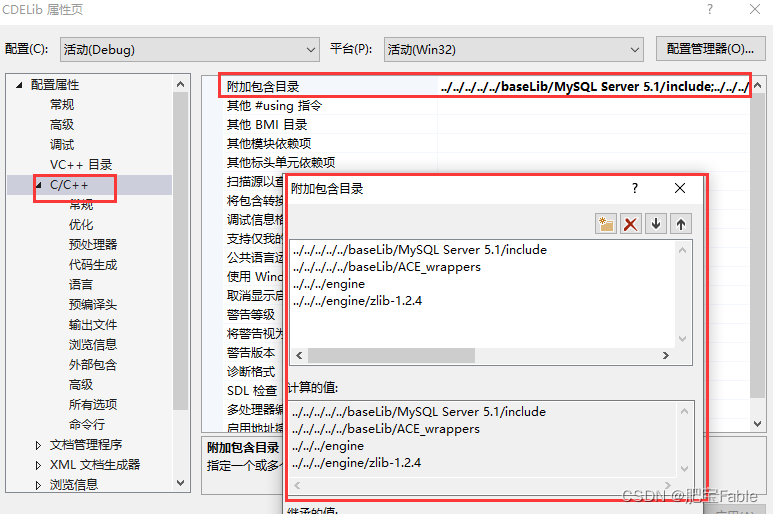
Windows环境下C++ 安装OpenSSL库 源码编译及使用(VS2019)
参考文章https://blog.csdn.net/xray2/article/details/120497146 之所以多次一举自己写多一篇文章,主要是因为原文内容还是不够详细。而且我安装的时候碰到额外的问题。 1.首先确认一下自己的代码是Win32的还是Win64的,我操作系统是64的,忘…...

TensorFlow高阶API和低阶API
TensorFlow提供了众多的API,简单地可以分类为高阶API和低阶API. API太多太乱也是TensorFlow被诟病的重点之一,可能因为Google的工程师太多了,社区太活跃了~当然后来Google也意识到这个问题,在TensorFlow 2.0中有了很大的改善。本文…...

强训之【参数解析和跳石板】
目录 1.参数解析1.1题目描述1.2思路1.3代码 2.跳石板2.1题目2.2思路2.3代码 3.选择题 1.参数解析 1.1题目描述 在命令行输入如下命令: xcopy /s c:\ d:\e, 各个参数如下: 参数1:命令字xcopy 参数2:字符串/s 参数…...

Redis队列Stream、Redis多线程详解(三)
Redis中的线程和IO模型 什么是Reactor模式 ? “反应”器名字中”反应“的由来: “反应”即“倒置”,“控制逆转”,具体事件处理程序不调用反应器,而向反应器注册一个事件处理器,表示自己对某些事件感兴趣࿰…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

