上海无纺布制造商【盈兹】申请纳斯达克IPO上市,募资1100万美元
来源:猛兽财经 作者:猛兽财经

猛兽财经获悉,来自上海的无纺布制造商【盈兹】,近期已向美国证券交易委员会(SEC)提交招股书,申请在纳斯达克IPO上市,股票代码为(ETZ),盈兹计划通过此次纳斯达克IPO上市以每股4.50美元的拟议中间价发行250万股股票,并募集1100万美元。
目前没有现有股东表示有兴趣以IPO时的价认购盈兹股票,如果盈兹在纳斯达克成功IPO上市,那么该公司在IPO时的市值将达到约8360万美元,不包括承销商超额配股权的影响。
公司业务
总部位于上海金山枫泾古镇的盈兹,成立于2016年,是一家无纺布制造商,致力于生产和销售无纺布及相关产品,目前主要是一次性非手术口罩和眼罩,该公司还寻求开始开发卫生用品,如成人纸尿裤和女性卫生护垫等。其销售区域覆盖美国、德国、西班牙、意大利、葡萄牙、荷兰、阿联酋、日本、韩国等国家。
盈兹目前拥有18项发明专利,23项实用新型专利。
主要采用最适合热风无纺布的法国安德里茨梳理机,加业内成熟可靠的台湾正纺烘箱,为客户提供高端热风无纺布及解决方案,目前盈兹的年产能为7200吨,由于热风无纺布对原料的依附性比较大,盈兹目前均采购Toyobo(东洋纺),Daiwabo(大和纺),Chisso,Far Eastern,Unitika等知名进口的ES复合纤维来保证原料的优质及稳定性。
盈兹的管理层由创始人、董事长兼首席执行官胡俊杰先生领导,胡俊杰自2016年公司成立以来一直在公司工作,此前曾担任3M中国的高级产品经理和RISI(专注于纸浆和造纸行业的咨询公司)的分析师。
截至2022年6月30日,盈兹已从投资者那里获得了470万美元的股权投资。
行业概况
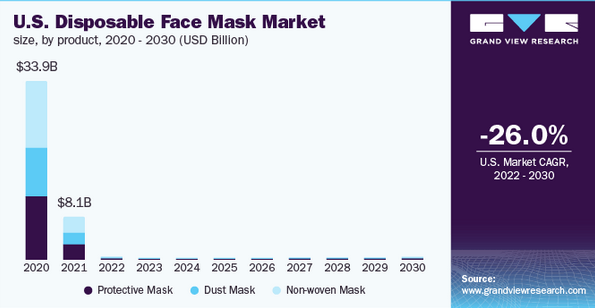
根据Grand View Research的市场研究报告,2021年全球一次性口罩市场的规模为389亿美元,预计到2030年将降至21亿美元。
这表示这个行业从2022年到2030年的预测复合年增长率为负(27.6%)。
预期需求下降的主要原因是疫情在2020年至2021年产生巨大的短期需求后,整体使用需求下降。
下图显示了一次性口罩产品在美国市场的历史和未来趋势:
盈兹在这个行业的主要竞争对手包括:
(1)3M
(2)霍尼韦尔(HON)
(3)金佰利(KMB)
(4)Uvex
(5)KOWA
(6)SAS Safety Corp
(7)The Gerson Company
(8)DACH
(9)Te Yin
财务情况
根据招股书,盈兹的财务情况如下:
收入下降,毛利润和毛利率降低,持续经营亏损和经营中使用的现金减少。
(1)总收入:盈兹2020年、2021年以及截至2022年6月30日的总收入分别为:4690万美元、1750万美元、541万美元。
(2)毛利润(亏损):盈兹2020年、2021年以及截至2022年6月30日的毛利润分别为:2458万美元、425万美元、70万美元。
(3)毛利率:盈兹2020年、2021年以及截至2022年6月30日的毛利率分别为:52.42%、24.30%、13.09%。
(4)营业利润(亏损):盈兹2020年、2021年以及截至2022年6月30日的营业利润分别为:1050万美元、281万美元、78万美元。
(5)综合收益(亏损):盈兹2020年、2021年以及截至2022年6月30日的综合收益分别为:1099万美元、259万美元、100万美元。
(6)经营性现金流:盈兹2020年、2021年以及截至2022年6月30日的经营性现金流分别为:1152万美元、331万美元、146万美元。
截至2022年6月30日,盈兹拥有330万美元现金和1370万美元的总负债。
截至2022年6月30日的12个月内,盈兹的自由现金流为负(380万美元)。
中介机构
Network 1 Securities是盈兹此次纳斯达克IPO上市的唯一承销商,该公司在过去12个月内领导的IPO自IPO以来产生了负的平均回报率(52.3%)。这是所有主要承销商在此期间的最低表现。
相关文章:

上海无纺布制造商【盈兹】申请纳斯达克IPO上市,募资1100万美元
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,来自上海的无纺布制造商【盈兹】,近期已向美国证券交易委员会(SEC)提交招股书,申请在纳斯达克IPO上市,股票代码为(ETZ&#…...
Build an SAP Fiori App(一)后面更新中
1.登录 SAP BTP Trial 地址: https://account.hanatrial.ondemand.com 流程可以参考 点击 serviced marketplace 搜索studio 点击创建 点击创建,点击view subscription 点击go to application 创建完成后 添加新链接 Field Value Name ES5 - if you’…...
关于GNSS技术介绍(二)
在上期文章中,我们介绍了GNSS技术的发展历程、原理,并对不同类型的定位技术进行了介绍,在本期文章中我们将继续讨论GNSS的优点与应用及其测试方法和解决方案。 GNSS的优点与应用 目前GNSS技术已经成为日常生活不可或缺的一部分,几…...

拿到新的服务器必做的五件事(详细流程,开发必看)
目录 1. 配置免密登录 基本用法 远程登录服务器: 第一次登录时会提示: 配置文件 创建文件 然后在文件中输入: 密钥登录 创建密钥: 2.部署nginx 一、前提条件 二、安装 Nginx 3.配置python虚拟环境 1.安装虚拟环境 …...

主机防病毒攻略之勒索病毒
勒索病毒并不是某一个病毒,而是一类病毒的统称,主要以邮件、程序、木马、网页挂马的形式进行传播,利用各种加密算法对文件进行加密,被感染者一般无法解密,必须拿到解密的私钥才有可能破解。 已知最早的勒索软件出现于 …...

Win10系统重装过程(一键装机)
相信不少小伙伴都有刷机重装系统的过程,那种镜像,up盘,压缩包等多个复杂过程也折磨的大伙不堪重负,因此本期带来简易版一键装机相应操作。 下载地址: 小心点击下方链接,点击即下载(3.66GB&…...

查询优化之单表查询
建表 CREATE TABLE IF NOT EXISTS article ( id INT(10) UNSIGNED NOT NULL PRIMARY KEY AUTO_INCREMENT, author_id INT(10) UNSIGNED NOT NULL, category_id INT(10) UNSIGNED NOT NULL, views INT(10) UNSIGNED NOT NULL, comments INT(10) UNSIGNED NOT NULL, title VARBI…...
ChatGPT写小论文
ChatGPT写小论文 只是个人对写小论文心得?从知乎,知网自己总结的,有问题,可以留个言我改一下 文章目录 ChatGPT写小论文-1.写论文模仿实战(狗头)0.论文组成1.好论文前提:2.标题3.摘要4.关键词5.概述6.实验数据、公式或者设计7.结论,思考8.参考文献 0.模仿1.喂大纲…...
公共资源包发布流程详解
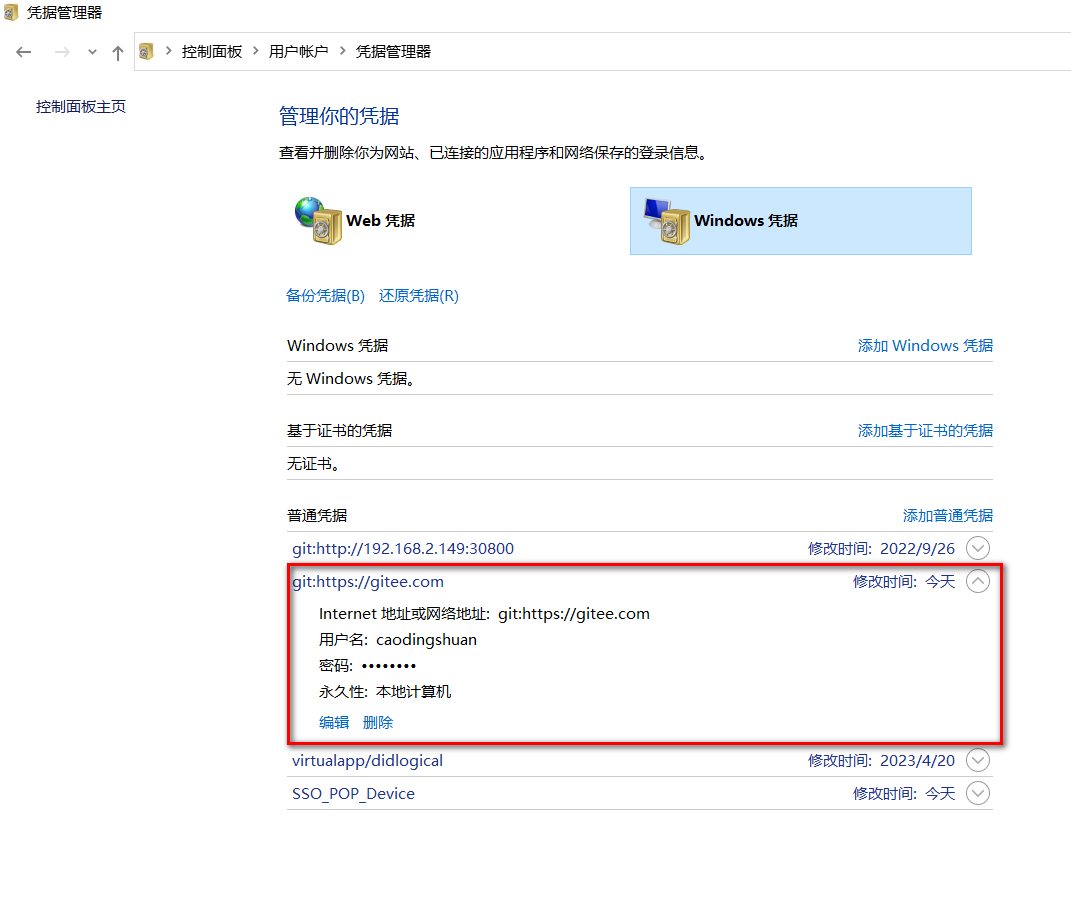
文章目录 公有包发布并使用npm安装git仓库协议创建及使用 npm 私有包创建及使用 group npm 私有包私有仓账密存放位置 当公司各个系统都需要使用特定的业务模块时,这时候将代码抽离,发布到 npm 上,供下载安装使用,是个比较好的方案…...
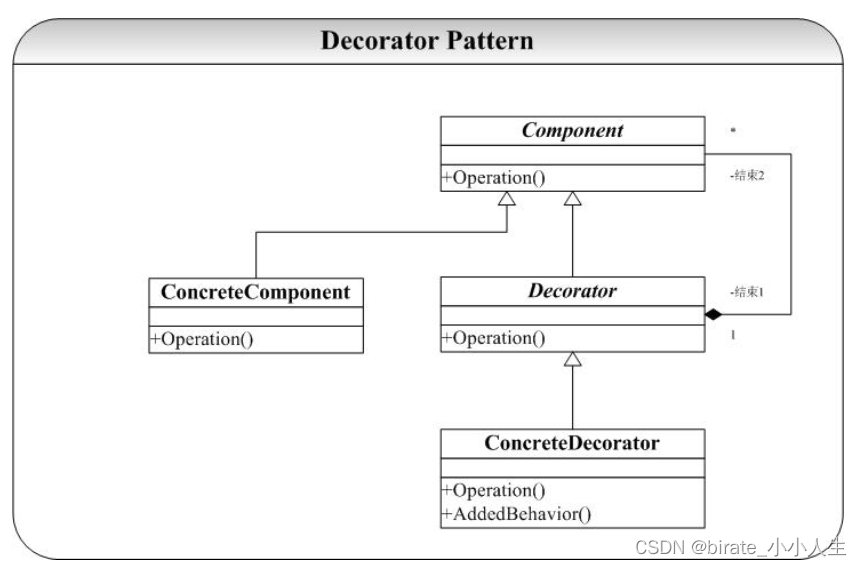
设计模式简谈
设计模式是我们软件架构开发中不可缺失的一部分,通过学习设计模式,我们可以更好理解的代码的结构和层次。 设计原则 设计原则是早于设计方法出现的,所以的设计原则都要依赖于设计方法。这里主要有八个设计原则。 推荐一个零声学院免费教程&…...

day35—选择题
文章目录 1.把逻辑地址转换程物理地址称为(B)2.在Unix系统中,处于(C)状态的进程最容易被执行3. 进程的控制信息和描述信息存放在(B)4.当系统发生抖动(thrashing)时,可以采取的有效措…...

mybatis的<foreach>标签使用
记录:419 场景:使用MyBatis的<foreach></foreach>标签的循环遍历List类型的入参。使用collection属性指定List,item指定List中存放的对象,separator指定分割符号,open指定开始字符,close指定结…...

干货 | 被抑郁情绪所困扰?来了解CBT吧!
Hello,大家好! 这里是 壹脑云科研圈 ,我是 喵君姐姐~ 我们的情绪就像是一组正弦波,有情绪很高涨的时刻,也会有情绪低落的瞬间,也会有情绪平稳的时候。 这种情绪上的变化非常正常,也正是因为这…...
每日一个小技巧:1招教你手机消除笔怎么用
在日常生活中,我们经常需要在手机上进行编辑和涂改,但是由于各种原因,我们可能会做出错误或者不满意的修改。这时候,消除笔就派上用场了。消除笔可以帮助我们在不影响其他内容的前提下,对错误或者不满意的修改进行撤销…...

4月26号软件更新资讯合集....
Tpflow V7.0.2,PHP 工作流引擎新版发布 欢迎使用 Tpflow V7.0.1 工作流引擎 TpFlow 工作流引擎是一套规范化的流程管理系统,基于业务而驱动系统生命力的一套引擎。彻底释放整个信息管理系统的的活力,让系统更具可用性,智能应用型…...

尚硅谷大数据项目【电商数仓5.0】学习笔记
尚硅谷大数据项目【电商数仓5.0】学习笔记 大数据学习基础 基础shell编程:大数据之基础shell 集群快速安装教程:大数据集群快速安装教程 注:如果您已经有大数据学习基础,可以通过上面教程快速搭建学习环境,如果您没…...
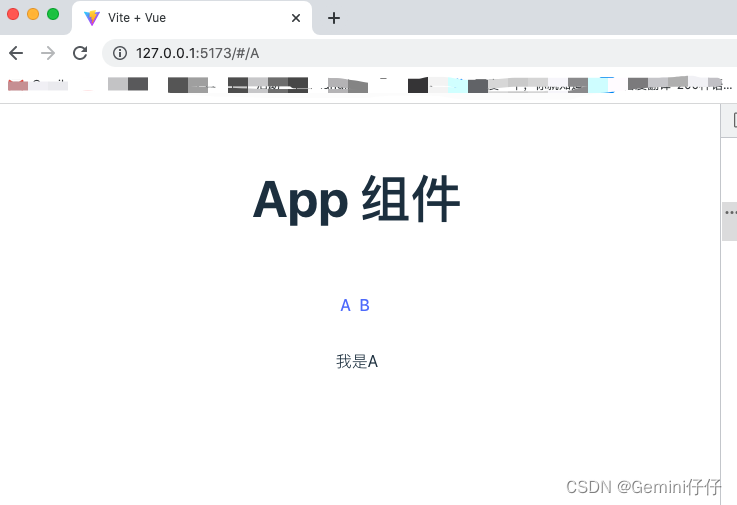
vue3配置router路由并实现页面跳转
1、安装vue-router 用vue3需要安装版本4.0以上的vue-router,安装命令: npm install vue-routernext --savevue2尽量安装4.0以下版本,安装命令: npm i vue-router3.1.3在package.json中可以查看vue-router版本号: 2、…...
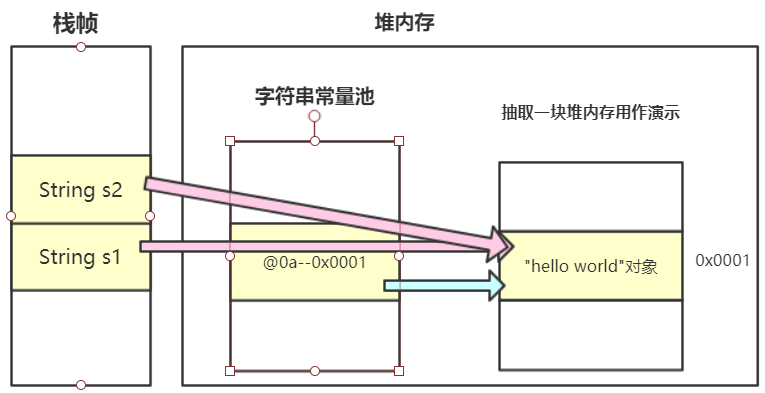
Java中字符串的初始化详解
前言 在深入学习字符串类之前,我们先搞懂JVM是怎样处理新生字符串的。当你知道字符串的初始化细节后,再去写String s "hello"或String s new String("hello")等代码时,就能做到心中有数。 首先得搞懂字符串常量池的概…...
-- 代码块)
面向对象(七)-- 代码块
目录 1. 代码块的概述 2. 代码块的分类 3. 代码块的执行优先级 1. 代码块的概述 在Java中,使用 { } 括起来的代码被称为代码块 2. 代码块的分...
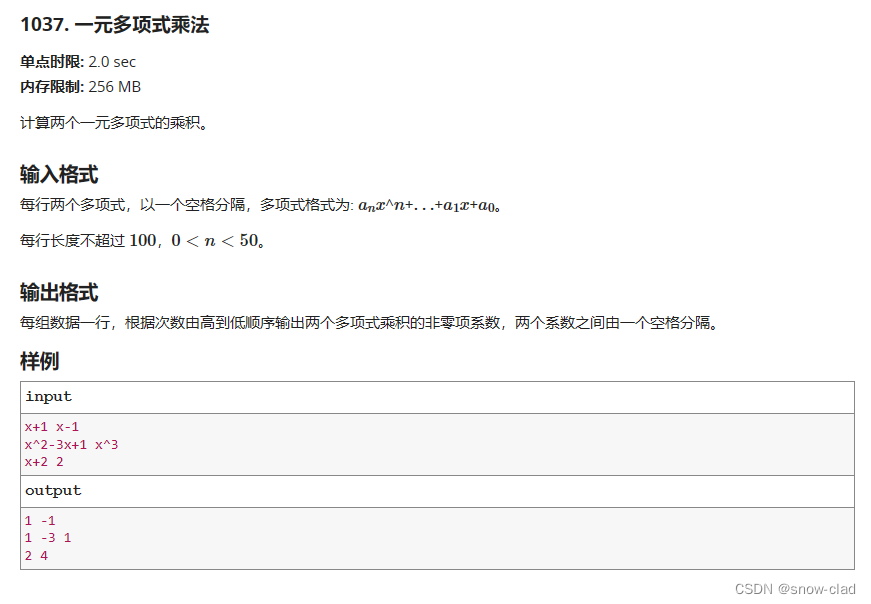
《编程思维与实践》1037.一元多项式乘法
《编程思维与实践》1037.一元多项式乘法 题目 思路 比较容易想到将步骤分为三步: 1.读取多项式每项的系数(coefficient)和对应的指数(dim); 2.进行多项式乘法; 3.输出进行多项式乘法后的非零项系数. 其中多项式乘法可以通过循环来处理,输出可以用if来判断系数是否为0,需要考虑…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
