【LeetCode】213. 打家劫舍 II
213. 打家劫舍 II(中等)



思路
这道题是 198.打家劫舍 的拓展版,区别在于:本题的房间是环形排列,而198.题中的房间是单排排列。
将房间环形排列,意味着第一间房间和最后一间房间不能同时盗窃,因此可以把这道题简化为两个单排排列的子问题。
- 可以选择第一个房间进行偷窃,也就是考虑
nums[0...n-2]; - 可以选择最后一个房间进行偷窃,也就是考虑
nums[1...n-1];
综合上述两种情况,选择偷窃金额最多的情况作为本题的答案。
状态定义
根据题解,本道题将定义两种状态:
first[i]:表示可以选择第一个房间的偷窃情况下,到第 i 个房间为止的最多金额;last[i]:表示可以选择最后一个房间的偷窃情况下,到第 i 个房间为止的最多金额;
状态转移方程
对于每个房间,都有偷窃和不偷窃两种选择,以第 i 个房间为例:
- 如果选择偷窃这个房间 i ,那么前一个房间肯定不能偷窃,所以当前的金额是第 i-2 个房间的金额加上该房间的现金,即
first[i] = first[i-2] + nums[i-1]; - 如果选择不偷窃该房间,所以当前的金额和前一个房间的金额相等,即
first[i] = first[i-1];
我们要得到偷窃到的最高金额,也就是在这两种情况中选择金额最高的,即 first[i] = max(first[i-1], first[i-2] + nums[i-1]);。
对于 last数组,它的状态转移方程是一致的。
初始化
first [0] = last[0] = 0;,第 0 个房间,也就意味着还没有实施偷窃,所以金额为 0;first[1] = nums[0] , last[1] = nums[1];first 和 last 的第一个房间的金额分别设置为 第一个房间的现金。
最终的返回结果
在题解中已经解释了,我们需要返回两种情况下的最大金额, 即 return max(first[n-1], last[n-1]); 。
代码
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();if(n<=3) return *max_element(nums.begin(), nums.end());vector first(n, 0);vector last(n, 0);first[1] = nums[0];for(int i=2; i<n; ++i){first[i] = max(first[i-1], first[i-2] + nums[i-1]);cout<<"i:"<<i<<" "<<first[i]<<endl;}last[1] = nums[1];for(int i=2; i<n; ++i){last[i] = max(last[i-1], last[i-2] + nums[i]);}return max(first[n-1], last[n-1]);}
};
空间压缩
由于 first[i] 只和前两个状态有关,因此可以进行空间压缩。
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();if(n<=3) return *max_element(nums.begin(), nums.end());int cur_first , pre1 = 0, pre2 = nums[0];for(int i=2; i<n; ++i){cur_first = max(pre2, pre1 + nums[i-1]);pre1 = pre2;pre2 = cur_first;}int cur_last;pre1 = 0, pre2 = nums[1];for(int i=2; i<n; ++i){cur_last = max(pre2, pre1 + nums[i]);pre1 = pre2;pre2 = cur_last;}return max(cur_first, cur_last);}
};
代码简化
显然,两个 for 循环的结构一致,所以可以将 for 循环写成子函数,也可以再定义两个变量,将两个 for循环整合到一起。这里只展示第二种写法:
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();if(n<=3) return *max_element(nums.begin(), nums.end());int cur_first ,cur_last;int pre1 = 0, pre2 = nums[0], pre3 = 0,pre4 = nums[1];for(int i=2; i<n; ++i){cur_first = max(pre2, pre1 + nums[i-1]);cur_last = max(pre4, pre3 + nums[i]);pre1 = pre2;pre2 = cur_first;pre3 = pre4;pre4 = cur_last;}return max(cur_first, cur_last);}
};
相关文章:

【LeetCode】213. 打家劫舍 II
213. 打家劫舍 II(中等) 思路 这道题是 198.打家劫舍 的拓展版,区别在于:本题的房间是环形排列,而198.题中的房间是单排排列。 将房间环形排列,意味着第一间房间和最后一间房间不能同时盗窃,因…...
从初识RabbitMQ到安装了解
一、同步和异步通讯 微服务间通讯有同步和异步两种方式: 同步通讯:就像打电话,需要实时响应。 异步通讯:就像发邮件,不需要马上回复。 两种方式各有优劣,打电话可以立即得到响应,但是你却不…...
-字符串函数的使用解析)
MySQL(六)-字符串函数的使用解析
字符串函数的使用解析 1 计算字符串字符数的函数和字符串长的函数2 合并字符串函数 CONCAT(s1,s2,...)、CONCAT_WS(xs1,s2,...)3 替换字符串函数INSERT(s1,x,len,s2)4 字母大小写转换函数5 获取指定长度的字符串的函数LEFT(s,n)和RIGHT(s,n)6 填充字符串的函数 LPAD(s1,len,s2)…...

Zookeeper集群搭建
搭建Zookeeper集群 1.1 搭建要求 真实的集群是需要部署在不同的服务器上的,但是在我们测试时同时启动很多个虚拟机内存会吃不消,所以我们通常会搭建伪集群,也就是把所有的服务都搭建在一台虚拟机上,用端口进行区分。 我们这里要…...
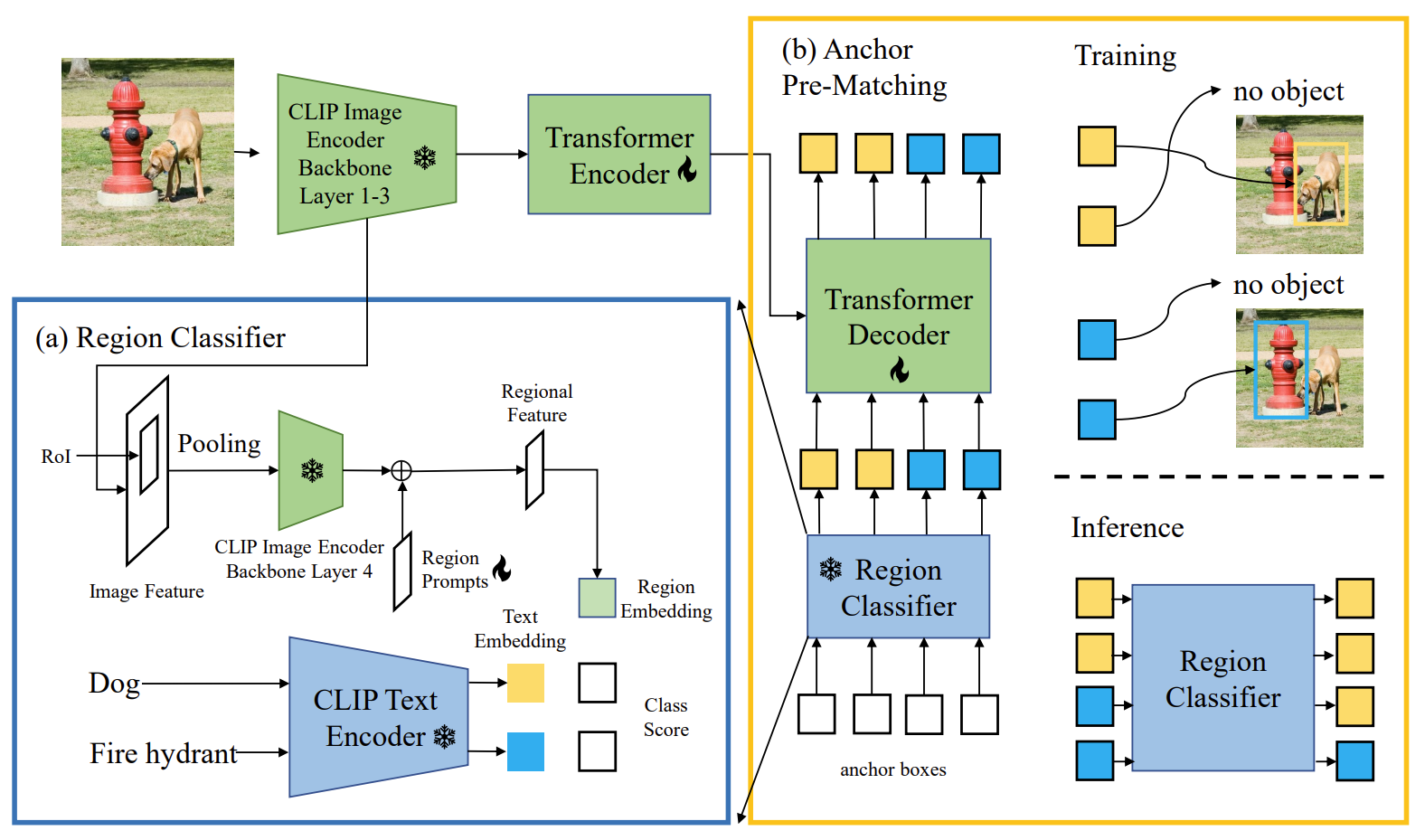
【计算机视觉 | 目标检测】OVD:Open-Vocabulary Object Detection 论文工作总结(共八篇)
文章目录 一、2D open-vocabulary object detection的发展和研究现状二、基于大规模外部图像数据集2.1 OVR-CNN:Open-Vocabulary Object Detection Using Captions,CVPR 20212.2 Open Vocabulary Object Detection with Pseudo Bounding-Box Labels&…...
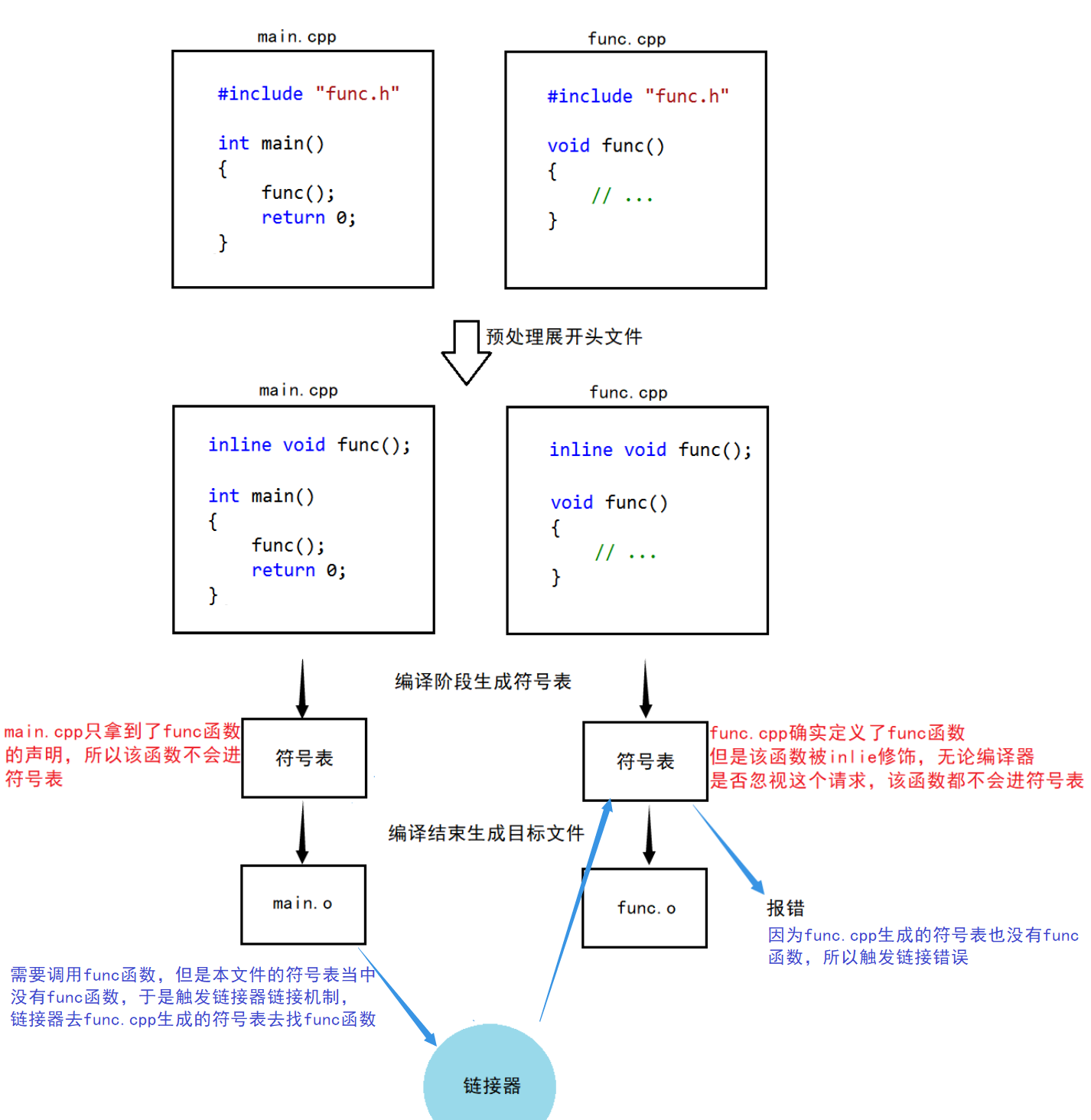
C++入门基础知识[博客园长期更新......]
0.博客园链接 博客的最新内容都在博客园当中,所有内容均为原创(博客园、CSDN同步更新)。 C知识点集合 1.命名空间 在往后的C编程中,将会存在大量的变量和函数,因为有大量的变量和函数,所以C的库会非常多。那么在C语言编程中&a…...
( “树” 之 BST) 501. 二叉搜索树中的众数 ——【Leetcode每日一题】
二叉查找树(BST):根节点大于等于左子树所有节点,小于等于右子树所有节点。 二叉查找树中序遍历有序。 ❓501. 二叉搜索树中的众数 难度:简单 给你一个含重复值的二叉搜索树(BST)的根节点 root…...
openharmony内核中不一样的双向链表
不一样的双向链表 链表初识别遍历双向链表参考链接 链表初识别 最近看openharmony的内核源码时看到一个有意思的双向链表,结构如下 typedef struct LOS_DL_LIST{struct LOS_DL_LIST *pstPrev; //前驱节点struct LOS_DL_LIST *pstNext; //后继节点 }LOS_DL_LIST;不…...

大文件删除不在回收站里怎么找回
在日常办公中,总会有一些新的文件产生,和用完后的文件清理掉。有时候不小心误删文件也是常有的事。但如果大文件删除不在回收站里怎么找回呢?遇到的小伙伴们请不要别急,只要按照下面的方法做就行了。 正常情况下删除会进入到回收站中&#x…...

Ubuntu22.04部署Pytorch2.0深度学习环境
文章目录 安装Anaconda创建新环境安装Pytorch2.0安装VS CodeUbuntu下实时查看GPU状态的方法小实验:Ubuntu、Windows10下GPU训练速度对比 Ubuntu安装完显卡驱动、CUDA和cudnn后,下面部署深度学习环境。 (安装Ubuntu系统、显卡驱动、CUDA和cudn…...

php的面试集结(会持续更新)
PHP 高级工程面试题汇总 php面试 1.大型的分页查询 发现当表中有很多上万条数据时,越后的数据用limit分页显示就越慢(>2秒),可能是mysql的特性所致。所以花了点时间总结实现了更优解决方案,最终实现毫秒级响应。…...

谁在成为产业经济发展的推车人?
区域发展的新蓝图中,京东云能做什么?它的角色是什么?这个问题背后,隐藏的不仅是京东云自身的能力和价值,更是其作为中国互联网云厂商的代表之一,对“技术产业”的新论证。 作者|皮爷 出品|产业家 关于云…...
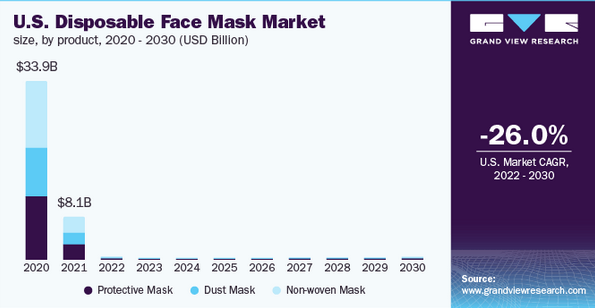
上海无纺布制造商【盈兹】申请纳斯达克IPO上市,募资1100万美元
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,来自上海的无纺布制造商【盈兹】,近期已向美国证券交易委员会(SEC)提交招股书,申请在纳斯达克IPO上市,股票代码为(ETZ&#…...
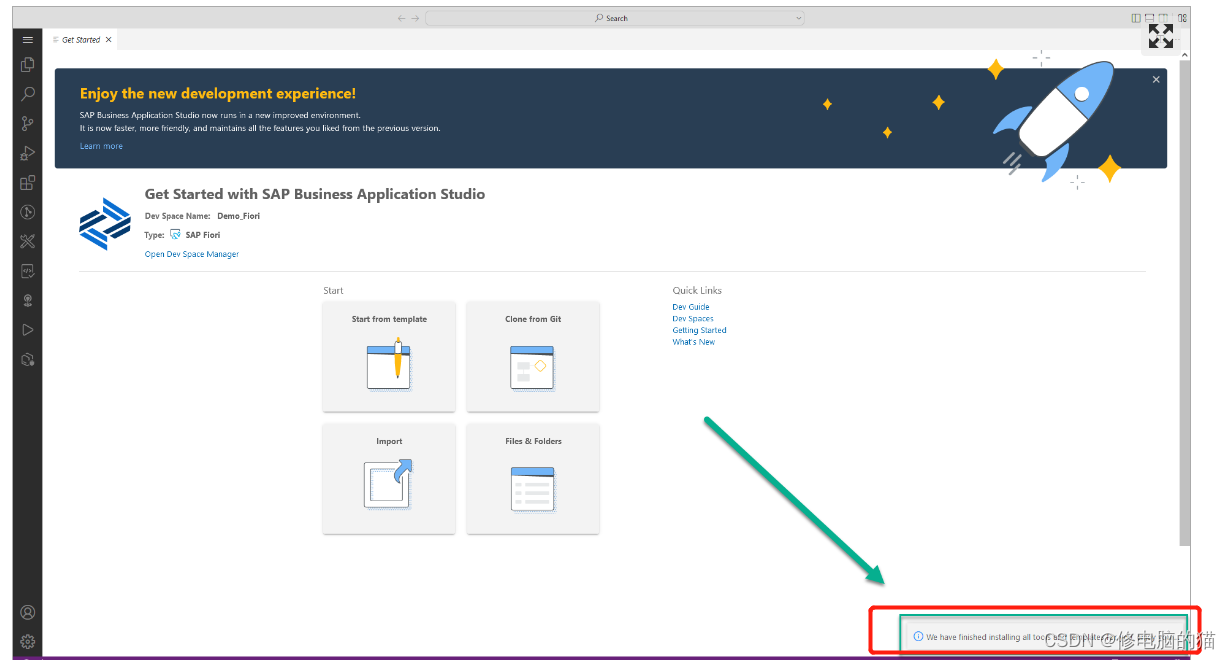
Build an SAP Fiori App(一)后面更新中
1.登录 SAP BTP Trial 地址: https://account.hanatrial.ondemand.com 流程可以参考 点击 serviced marketplace 搜索studio 点击创建 点击创建,点击view subscription 点击go to application 创建完成后 添加新链接 Field Value Name ES5 - if you’…...
关于GNSS技术介绍(二)
在上期文章中,我们介绍了GNSS技术的发展历程、原理,并对不同类型的定位技术进行了介绍,在本期文章中我们将继续讨论GNSS的优点与应用及其测试方法和解决方案。 GNSS的优点与应用 目前GNSS技术已经成为日常生活不可或缺的一部分,几…...

拿到新的服务器必做的五件事(详细流程,开发必看)
目录 1. 配置免密登录 基本用法 远程登录服务器: 第一次登录时会提示: 配置文件 创建文件 然后在文件中输入: 密钥登录 创建密钥: 2.部署nginx 一、前提条件 二、安装 Nginx 3.配置python虚拟环境 1.安装虚拟环境 …...

主机防病毒攻略之勒索病毒
勒索病毒并不是某一个病毒,而是一类病毒的统称,主要以邮件、程序、木马、网页挂马的形式进行传播,利用各种加密算法对文件进行加密,被感染者一般无法解密,必须拿到解密的私钥才有可能破解。 已知最早的勒索软件出现于 …...

Win10系统重装过程(一键装机)
相信不少小伙伴都有刷机重装系统的过程,那种镜像,up盘,压缩包等多个复杂过程也折磨的大伙不堪重负,因此本期带来简易版一键装机相应操作。 下载地址: 小心点击下方链接,点击即下载(3.66GB&…...

查询优化之单表查询
建表 CREATE TABLE IF NOT EXISTS article ( id INT(10) UNSIGNED NOT NULL PRIMARY KEY AUTO_INCREMENT, author_id INT(10) UNSIGNED NOT NULL, category_id INT(10) UNSIGNED NOT NULL, views INT(10) UNSIGNED NOT NULL, comments INT(10) UNSIGNED NOT NULL, title VARBI…...
ChatGPT写小论文
ChatGPT写小论文 只是个人对写小论文心得?从知乎,知网自己总结的,有问题,可以留个言我改一下 文章目录 ChatGPT写小论文-1.写论文模仿实战(狗头)0.论文组成1.好论文前提:2.标题3.摘要4.关键词5.概述6.实验数据、公式或者设计7.结论,思考8.参考文献 0.模仿1.喂大纲…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...
